Maximize your online presence with our exclusive offer: Get a stunning hero banner, the hero you need and deserve, at an unbeatable price! Bew, 689282782, bupparchard@gmail.com

Resources

The Big Naughty List

Definition and examples. Derivatives of Trigonometric, Inverse and Exponential and Logarithms Functions. General rules. Higher Derivatives. Implicit Differentiation Read more... 1026 words,🕔5 minutes read, May 14, 2022.

Basic Maths

Natural Numbers

Natural numbers are those used for counting and ordering. We use numbers in our daily lives more often than we realize. Know more about natural numbers with us. Read more... 174 words,🕔1 minutes read, May 12, 2022.

Natural numbers II

Natural numbers are those used for counting and ordering. Know more about natural numbers and how to learn basic arithmetic fast and easy. Read more... 2205 words,🕔11 minutes read, May 13, 2022.

Elementary Maths

Learn Math with us easily. We are talking about divisors, prime numbers, prime factorization, gcd, lcm, numeric systems, and more. Read more... 2519 words,🕔12 minutes read, May 13, 2022.

Learn Geometry with GeoGebra

GeoGebra is a free dynamic mathematics software and it is especially created for teaching and learning. Let's learn basic Geometry with Geogebra. Read more... 2357 words,🕔12 minutes read, May 14, 2022.

What is the best Maths software to learn and grow?

Do you have Maths homework? How do you know that your results are OK? This article is going to teach you how to use easy-to-use, free-of-charge software to check that your calculations are correct Read more... 970 words,🕔5 minutes read, Mar 22, 2022.

Fractions are really cool!

A fraction is a fancy way of representing the division of a whole into parts. Learn fractions with us in a fun and engaging way. Read more... 921 words,🕔5 minutes read, May 14, 2022.

Decimals, Percentages, Mixed numbers, and improper fractions

Decimals, fractions, and percentages are, basically, alternative ways of representing the same value. Learn fractions with us in a fun and engaging way. Read more... 891 words,🕔5 minutes read, May 14, 2022.

Sets and Operations on Sets

A set is a collection of things or objects, such as animals, plants, vowels. Learn all about sets and set operations. Read more... 1429 words,🕔7 minutes read, May 15, 2022.

Polynomials, Equations, and Systems of equations

The step by step guide to learn everything that you need to know about polynomials, equations, and systems of equations. Read more... 2785 words,🕔14 minutes read, May 15, 2022.

Plotting functions

The step by step guide to learn everything that you need to know about functions and plotting their graphs. Read more... 3245 words,🕔16 minutes read, May 16, 2022.

Plotting functions II

The step by step guide to learn everything that you need to know about functions and plotting their graphs. Increasing and decreasing functions. Maximum and Minimum. Asymptotes. Convex functions. Data Visualization. Read more... 3661 words,🕔18 minutes read, May 17, 2022.

Statistics

A step by step guide to analyzing and interpreting data using LibreOffice Calc and R. R is a free programming language and statistical software for analyzing and visualizing data. Read more... 3026 words,🕔15 minutes read, May 18, 2022.

Statistics II. Chi-squared Test, ANOVA

A step by step guide to analyzing and interpreting data using LibreOffice Calc and R. Let's go deeper and study the Chi-squared Test of Independence, one-way and two-way ANOVA, and two-way repeated measures ANOVA. Read more... 5104 words,🕔24 minutes read, May 18, 2022.

Statistics III. T-tests, Correlations, Linear, and Multilinear Regression

This is the final article of a three-part blog series on analyzing and interpreting data. Today, we will learn about T-tests, correlations, lineal, and multilinear regressions. Read more... 5048 words,🕔24 minutes read, May 19, 2022.

Mathematical analysis

A brief, quick and dirty, introduction to Mathematical Analysis with Maxima, Python, and WolframAlpha. We will learn about functions, limits, derivatives, integrals, and series. Read more... 2929 words,🕔14 minutes read, May 20, 2022.

How to convert units

Unit conversion is the process of converting a quantity from one base or unit of measurement to another by multiplying or dividing it by a conversion factor. Read more... 837 words,🕔4 minutes read, Aug 10, 2017.

How to use a calculator and how to measure objects

A calculator is a small electronic device or software application that can perform mathematical calculations. Screen rulers let you measure objects easily. Read more... 1187 words,🕔6 minutes read, Aug 10, 2017.

Complex Numbers

The easy-to-follow step by step guide to learn everything that you need to know about complex numbers. Learn to check the validity of your calculations with Octave, Python, and WolframAlpha. Read more... 1955 words,🕔10 minutes read, May 21, 2022.

Vectors, matrices, and system of linear equations

A step by step guide to learn everything that you need to know about vectors and matrices, as well as solving linear equations with many examples. Read more... 3026 words,🕔15 minutes read, May 21, 2022.

LibreOffice Math and LaTeX

LaTeX is a high-quality typesetting system; it includes features designed for the production of technical and scientific documentation. Python and LaTeX. Render LaTeX math expressions in Hugo Read more... 1220 words,🕔6 minutes read, May 22, 2022.

Topology

Topology Spaces

Topology Spaces. Definition and examples. Read more... 1999 words,🕔10 minutes read, May 14, 2022.

Convergence

Limit and isolated points. Dense sets. Convergence of sequences. Read more... 426 words,🕔2 minutes read, May 14, 2022.

Linear Algebra

System of linear equations

Topology Spaces. Definition and examples. Read more... 1085 words,🕔6 minutes read, May 14, 2022.

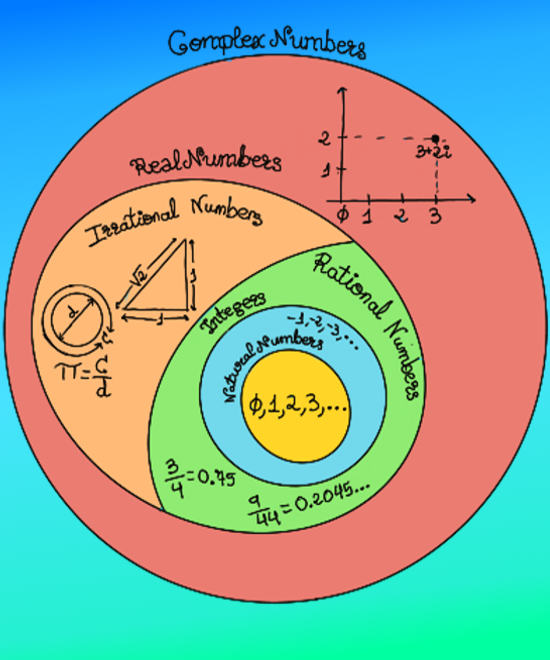
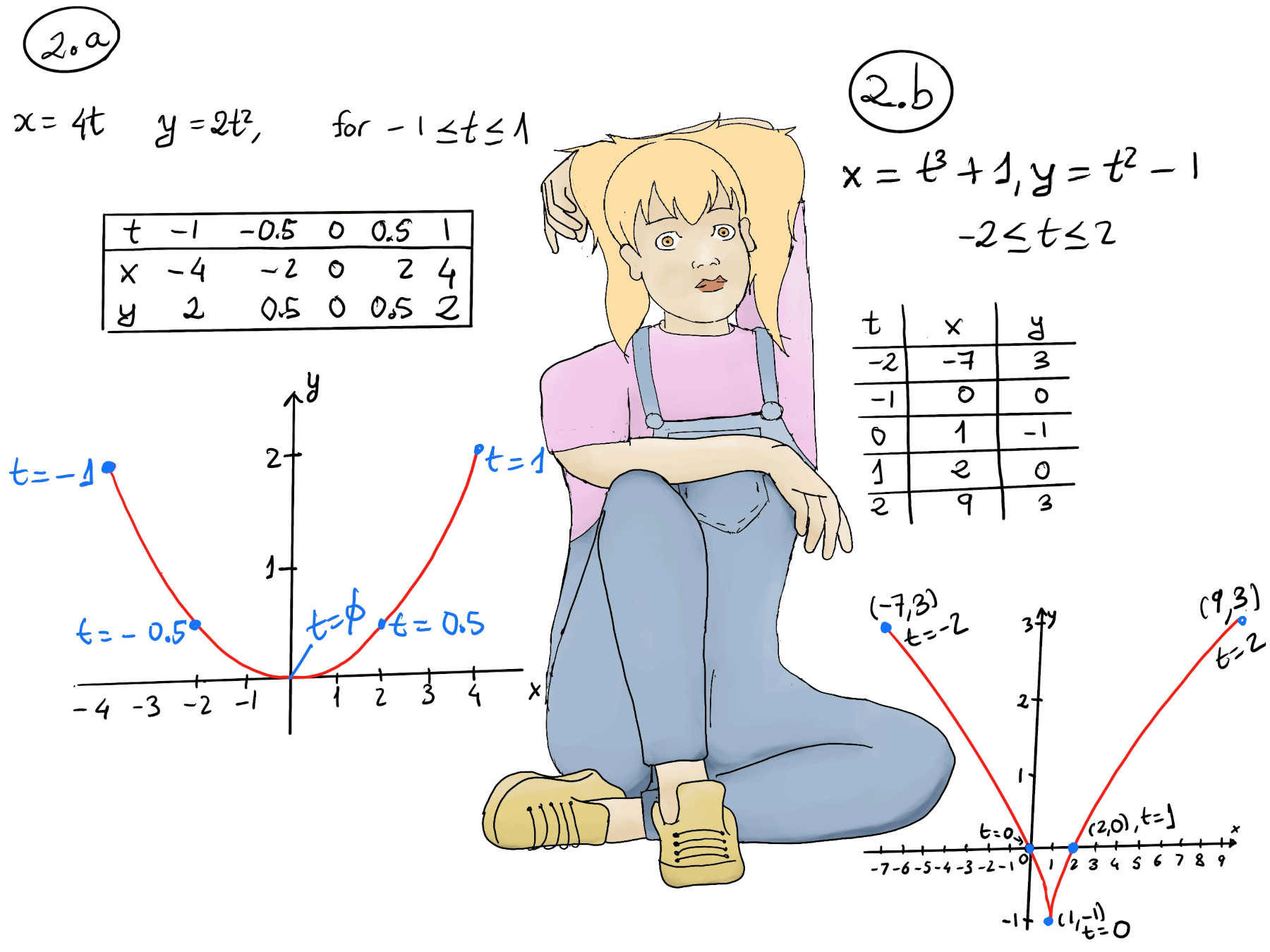
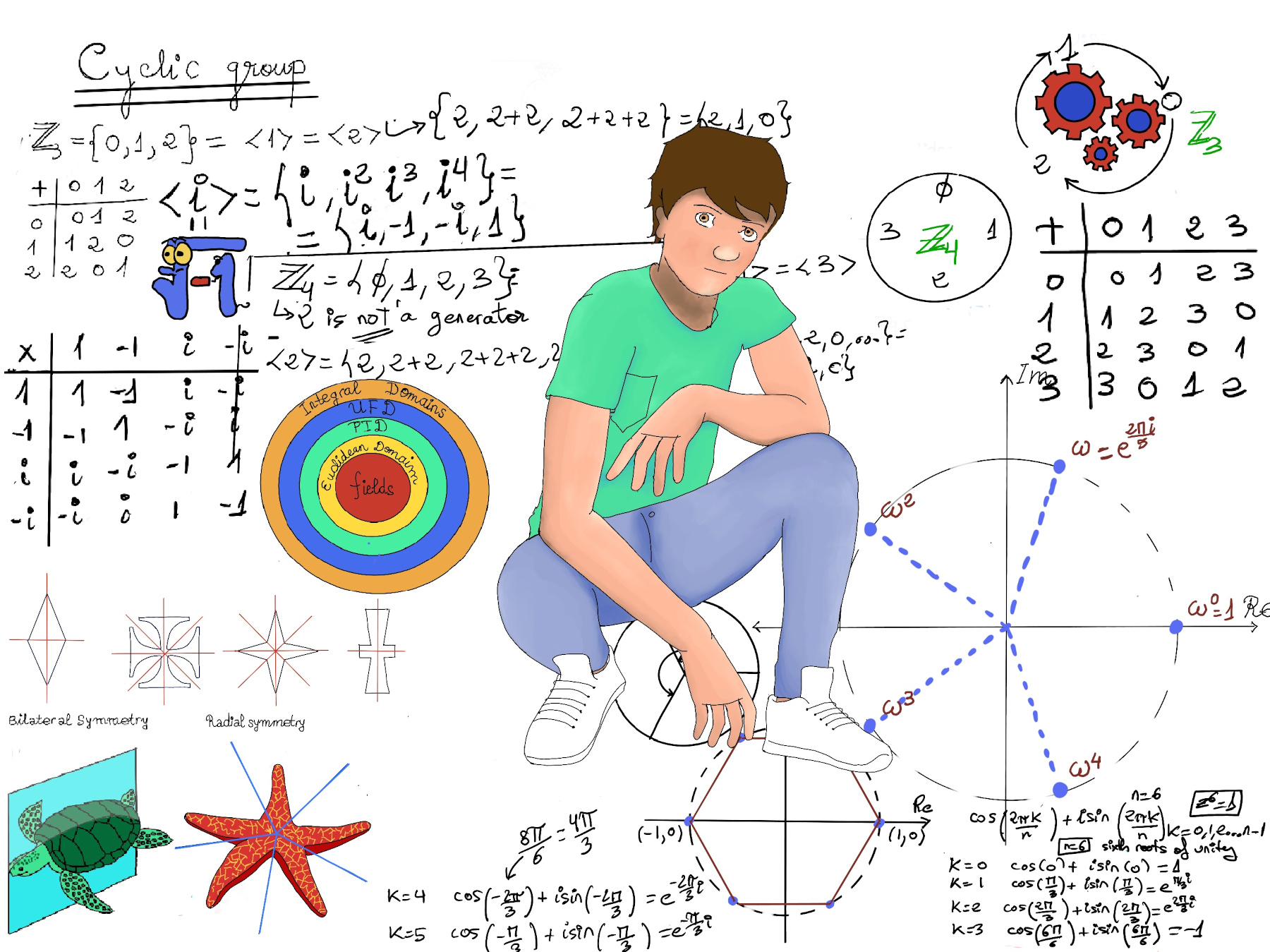
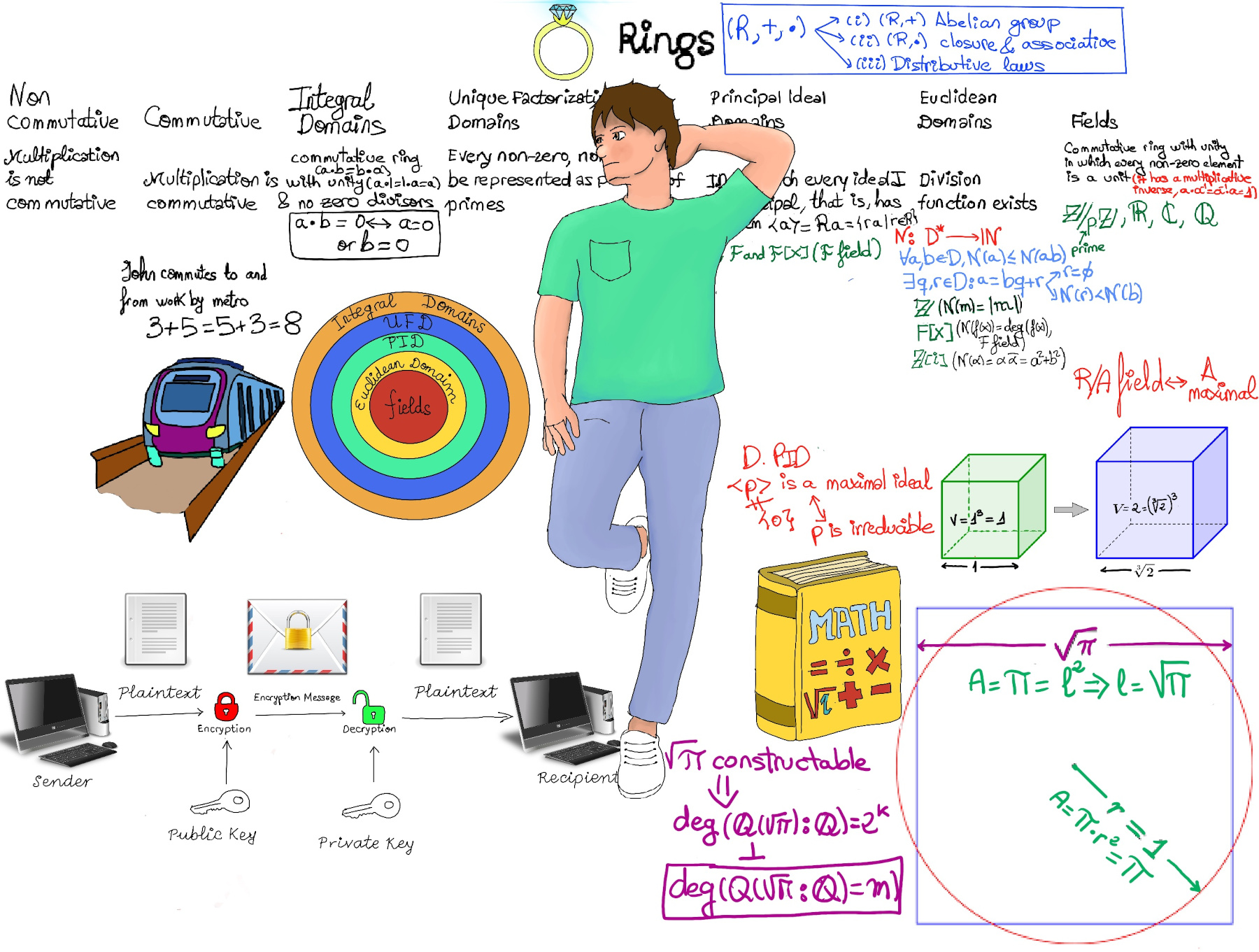
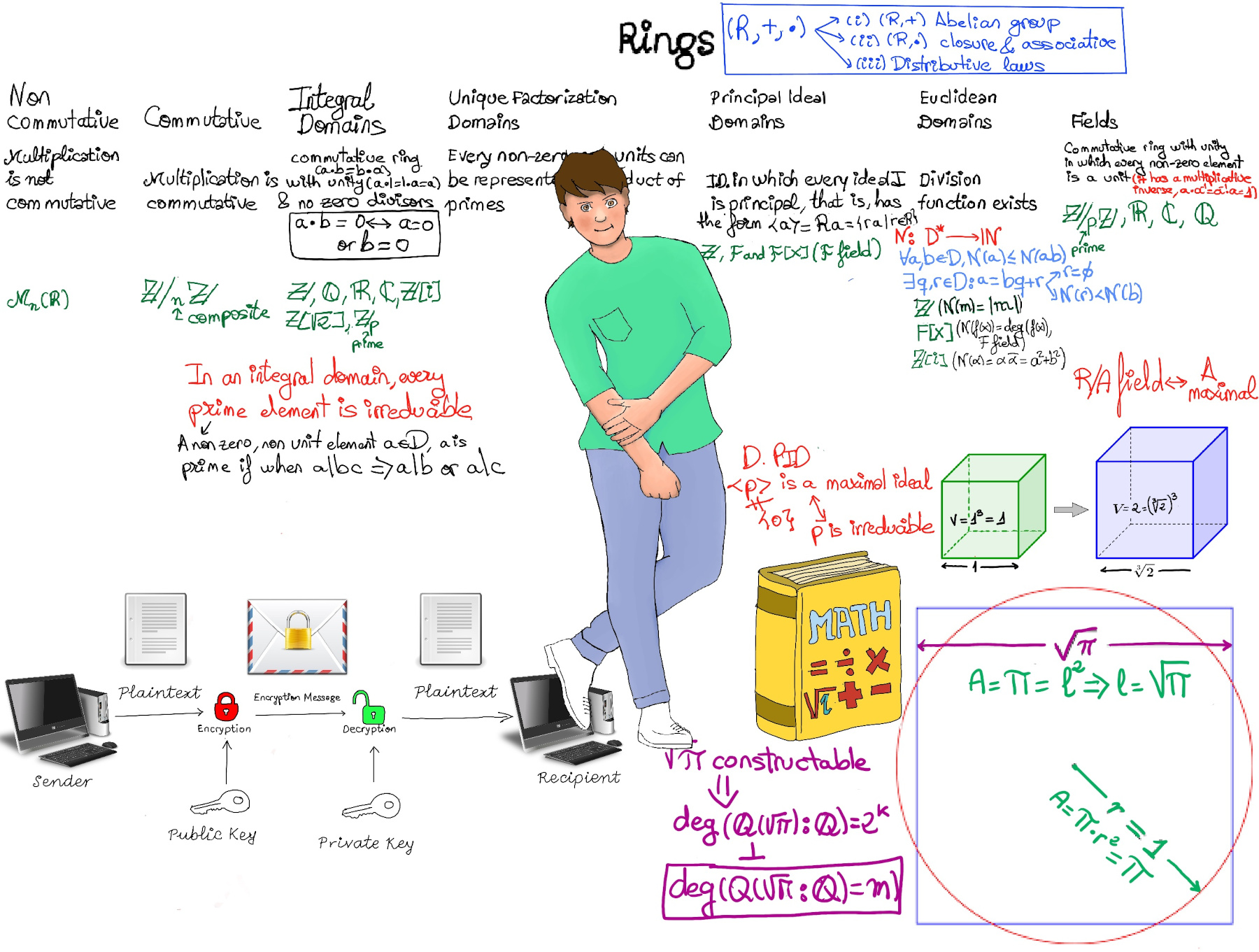
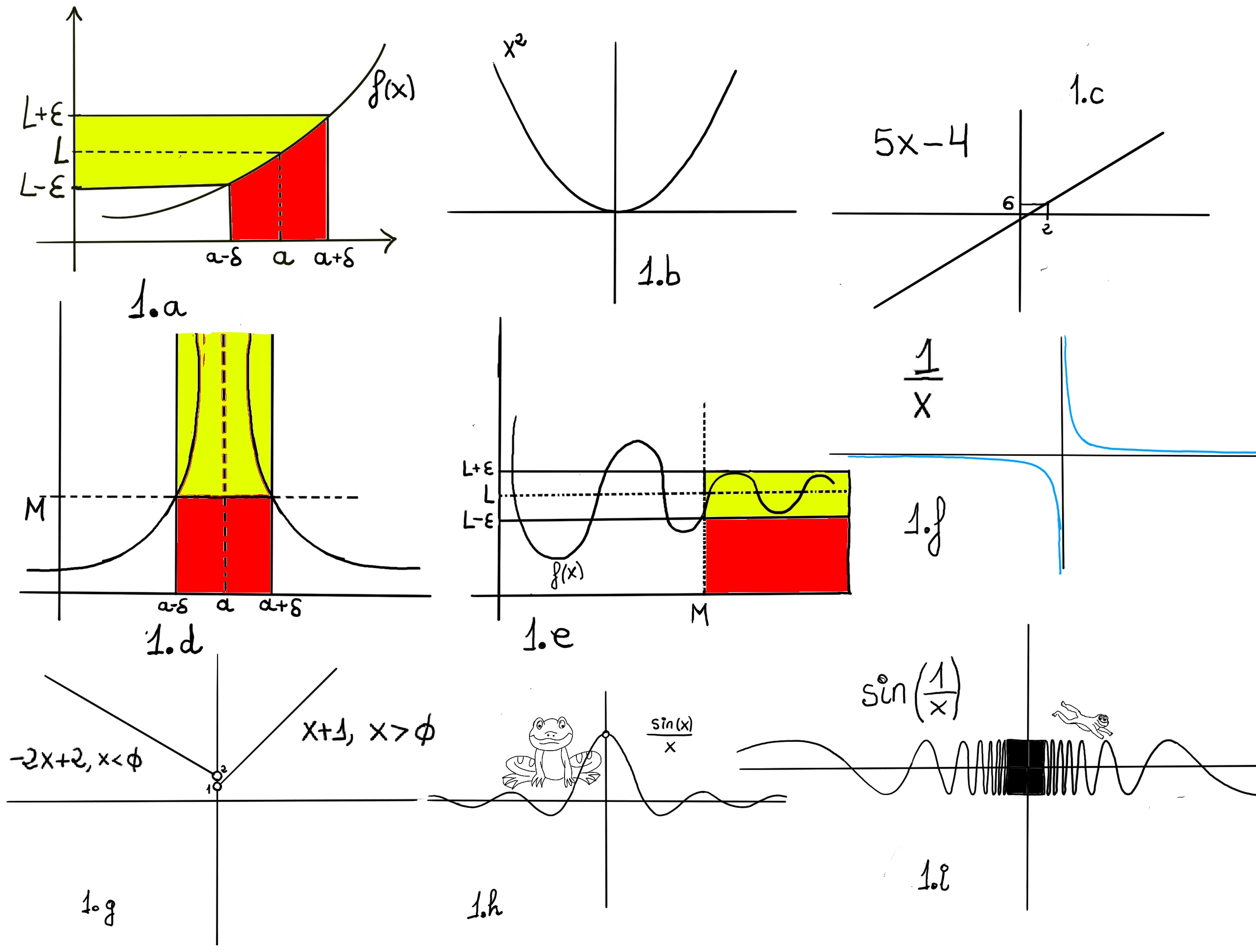
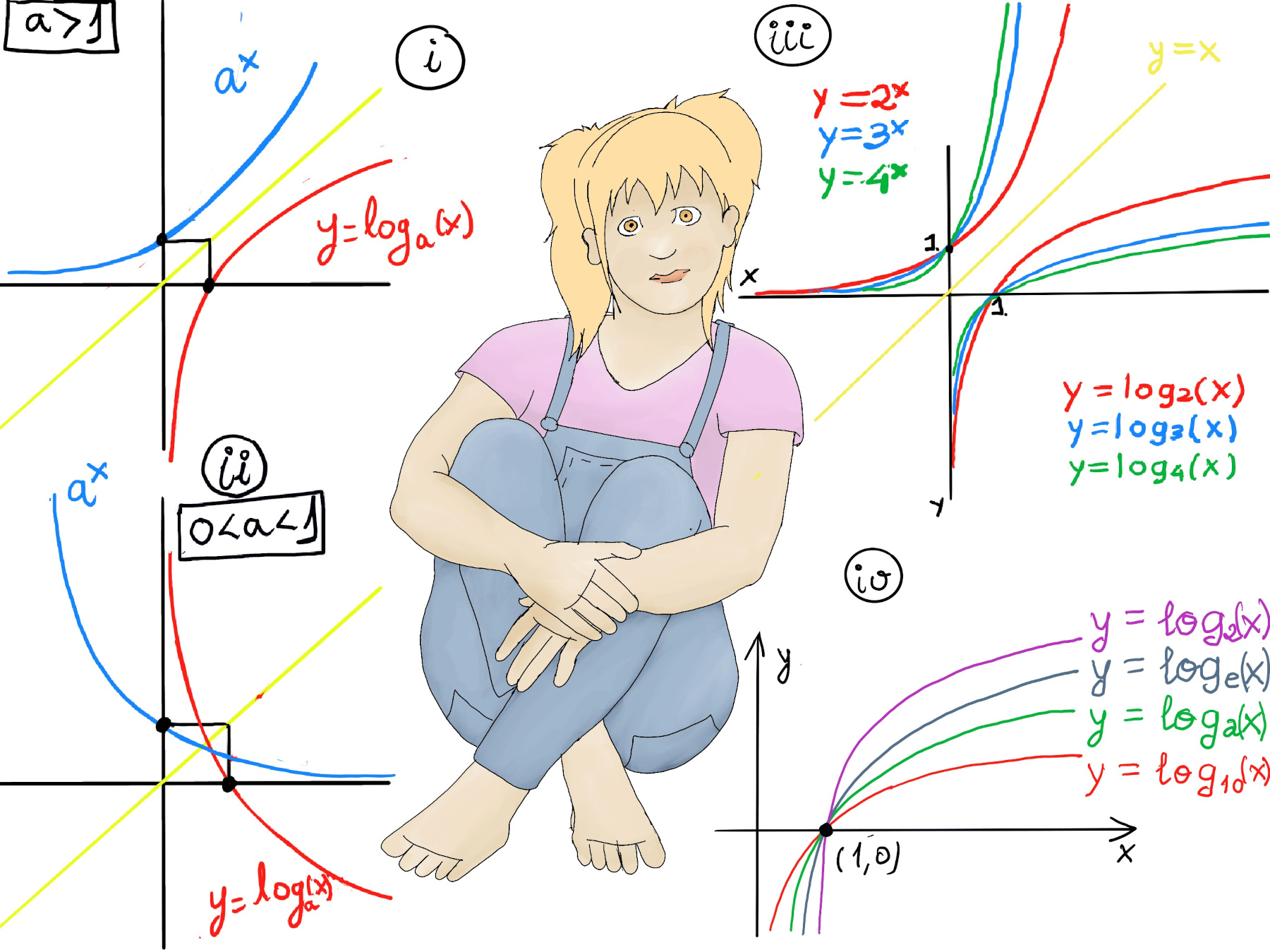
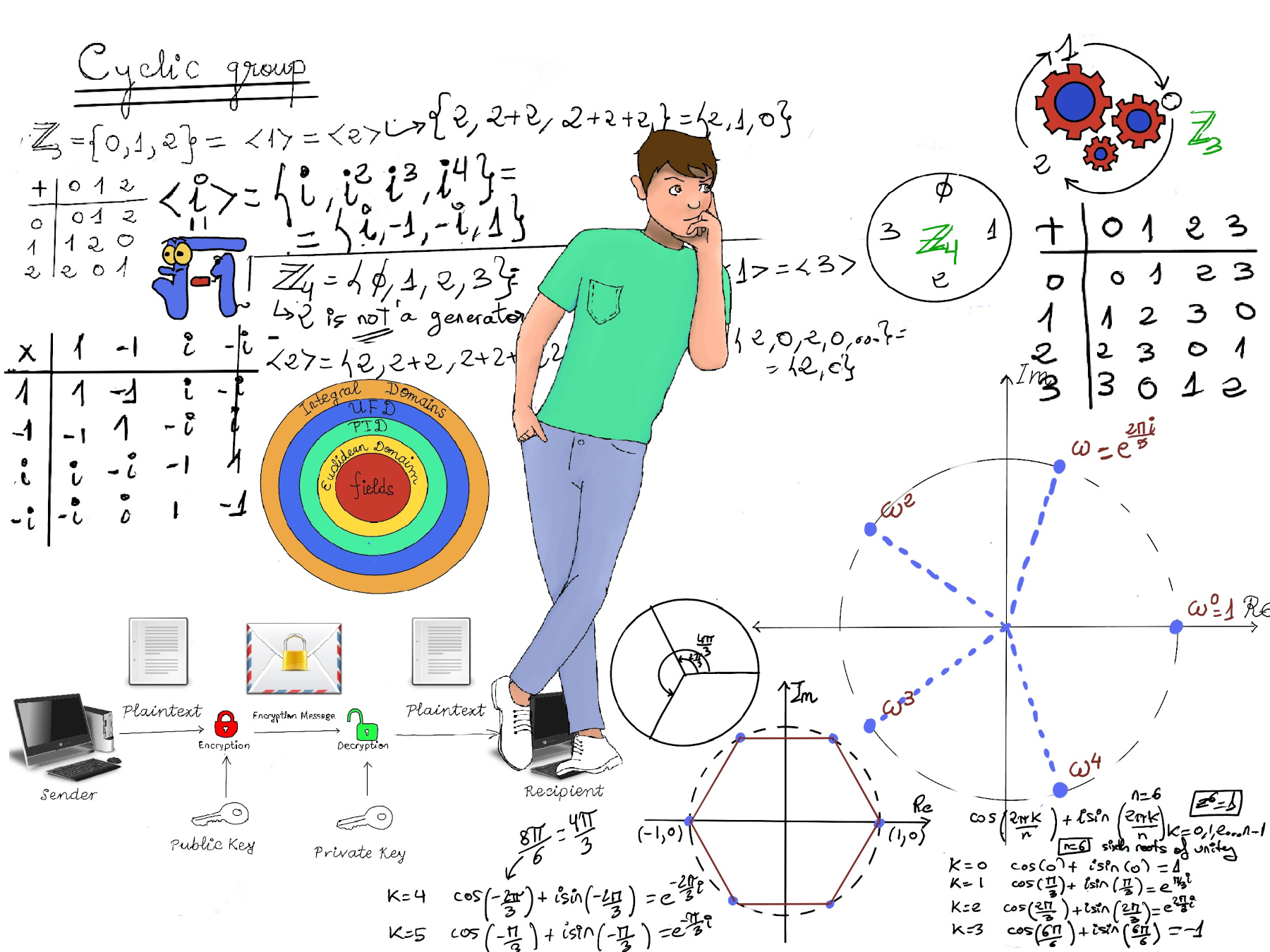
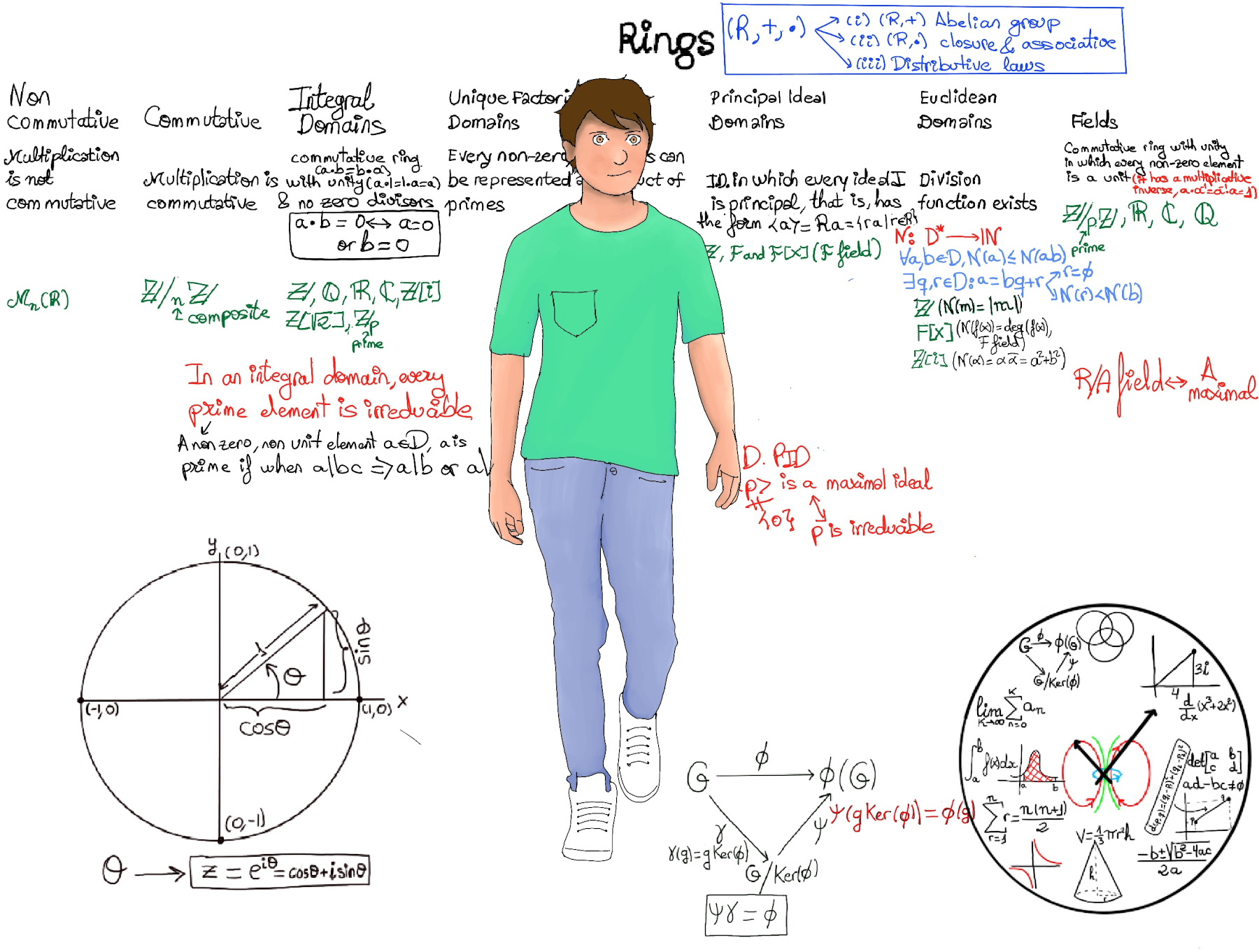
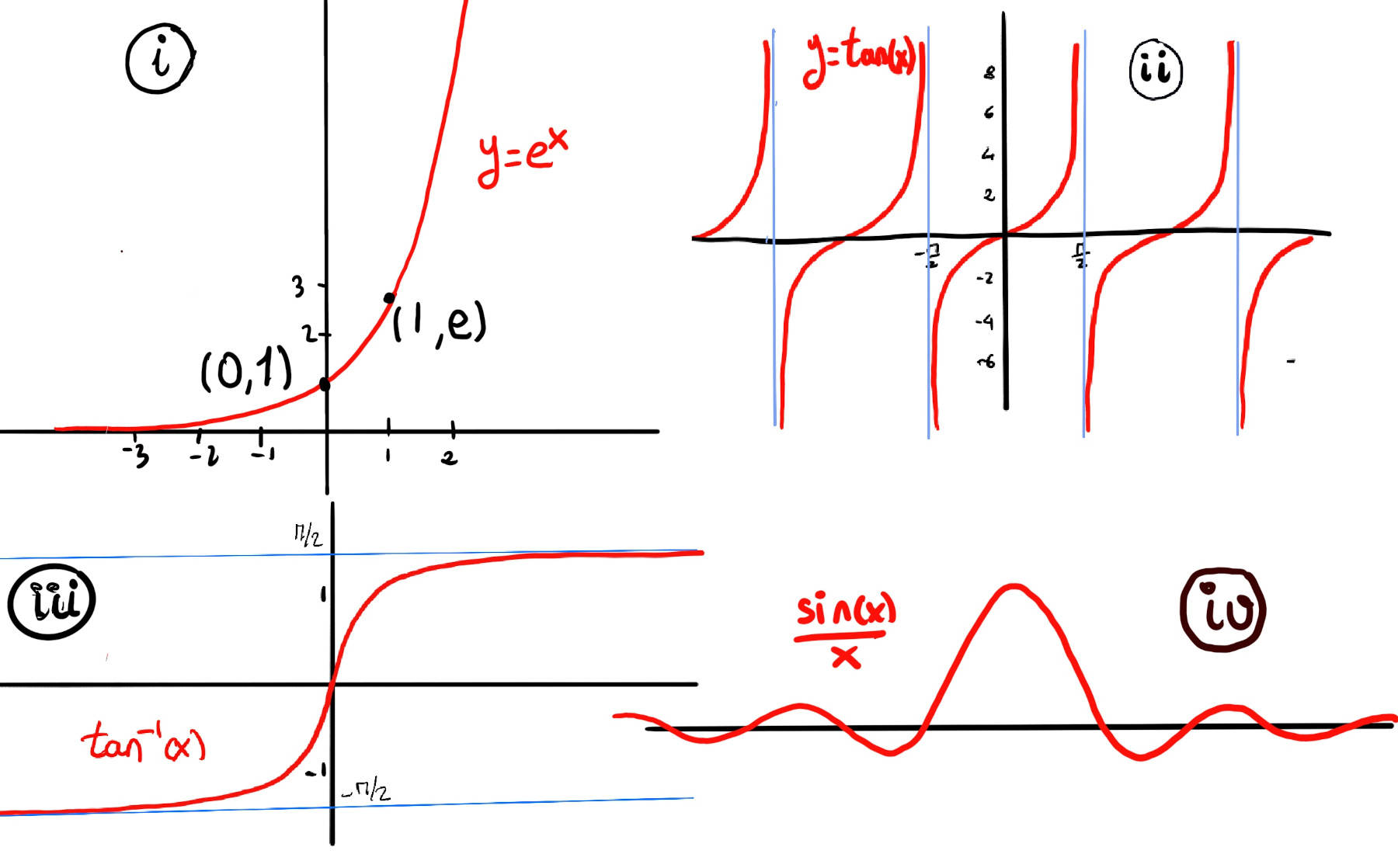
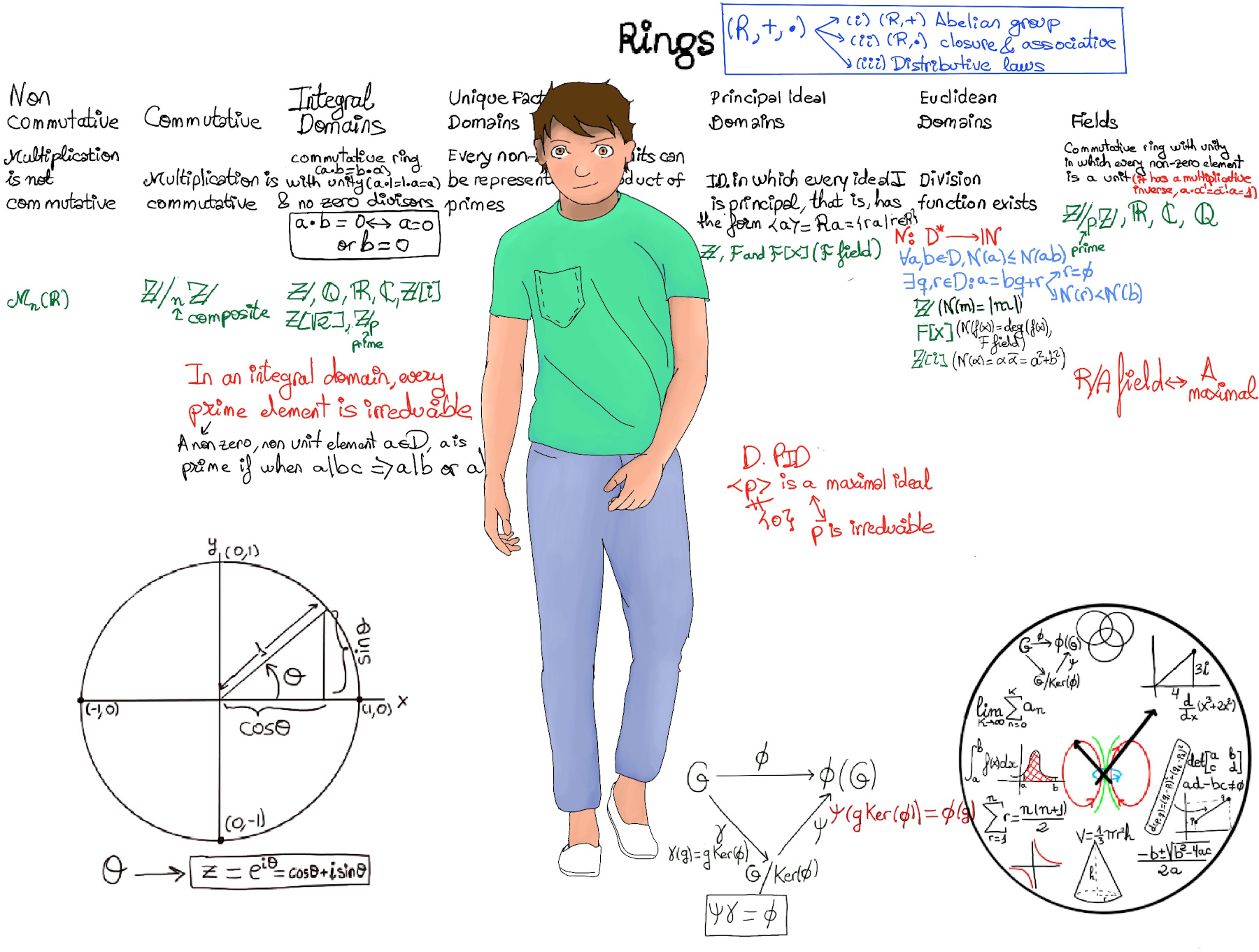
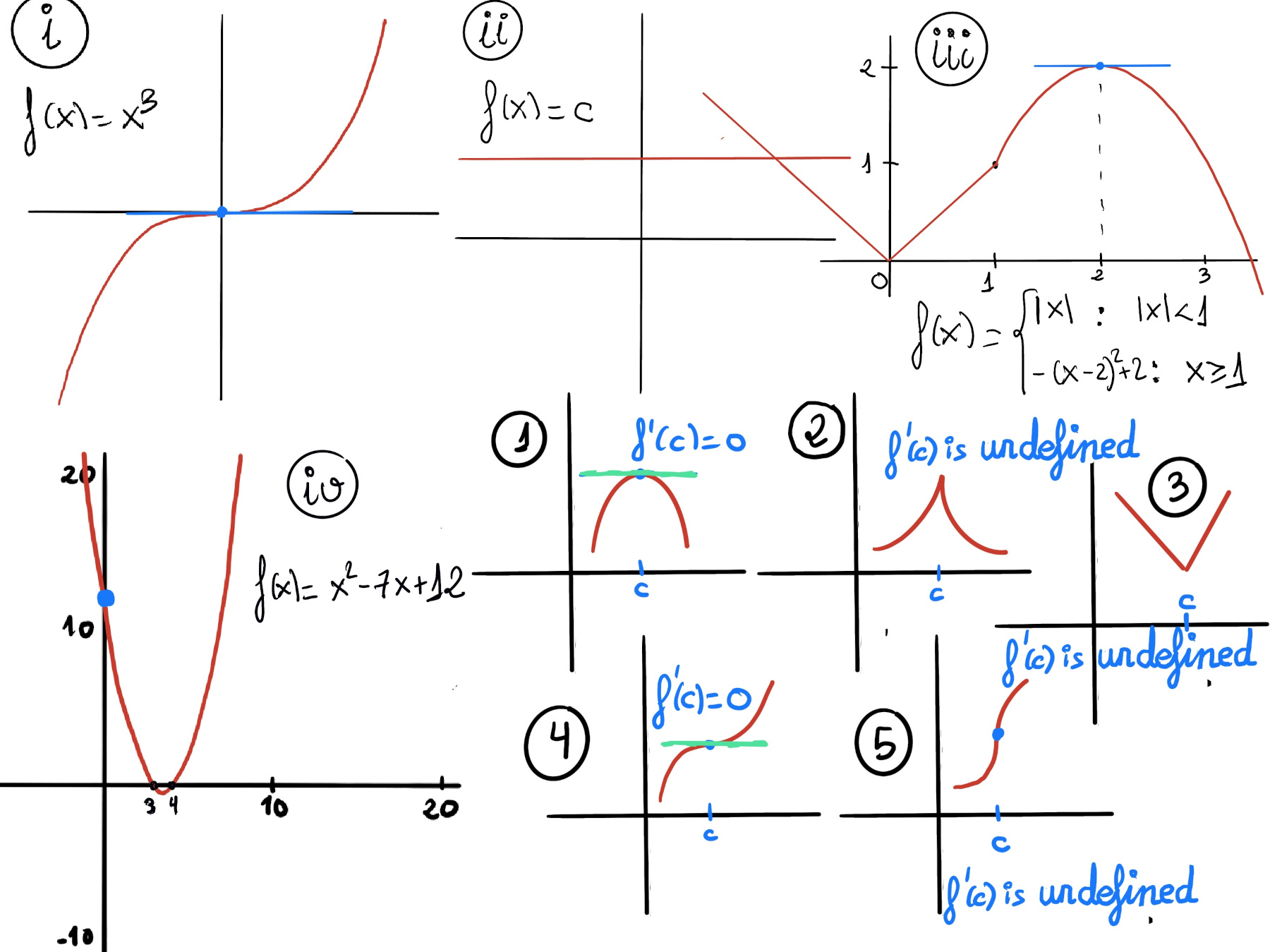
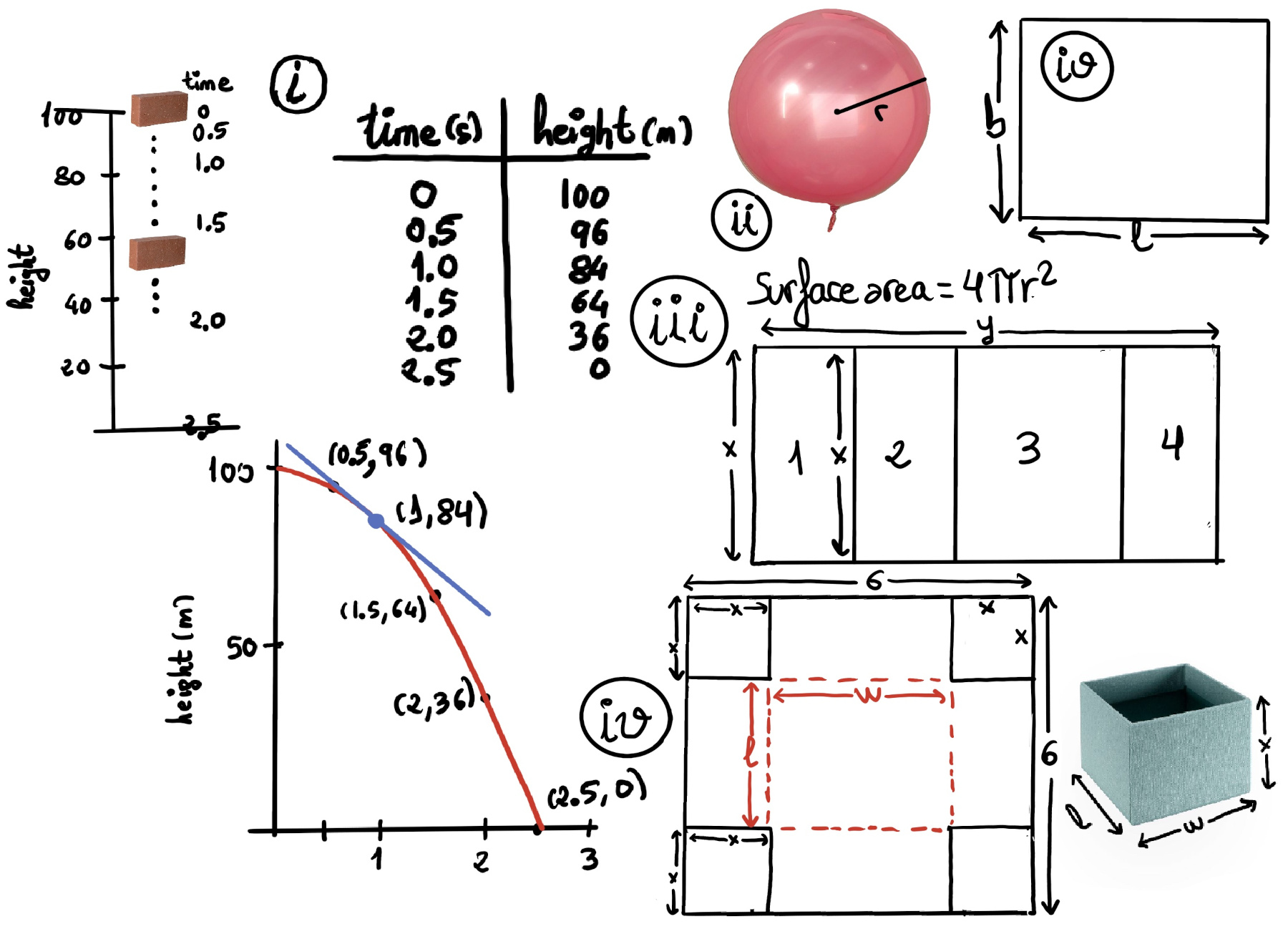
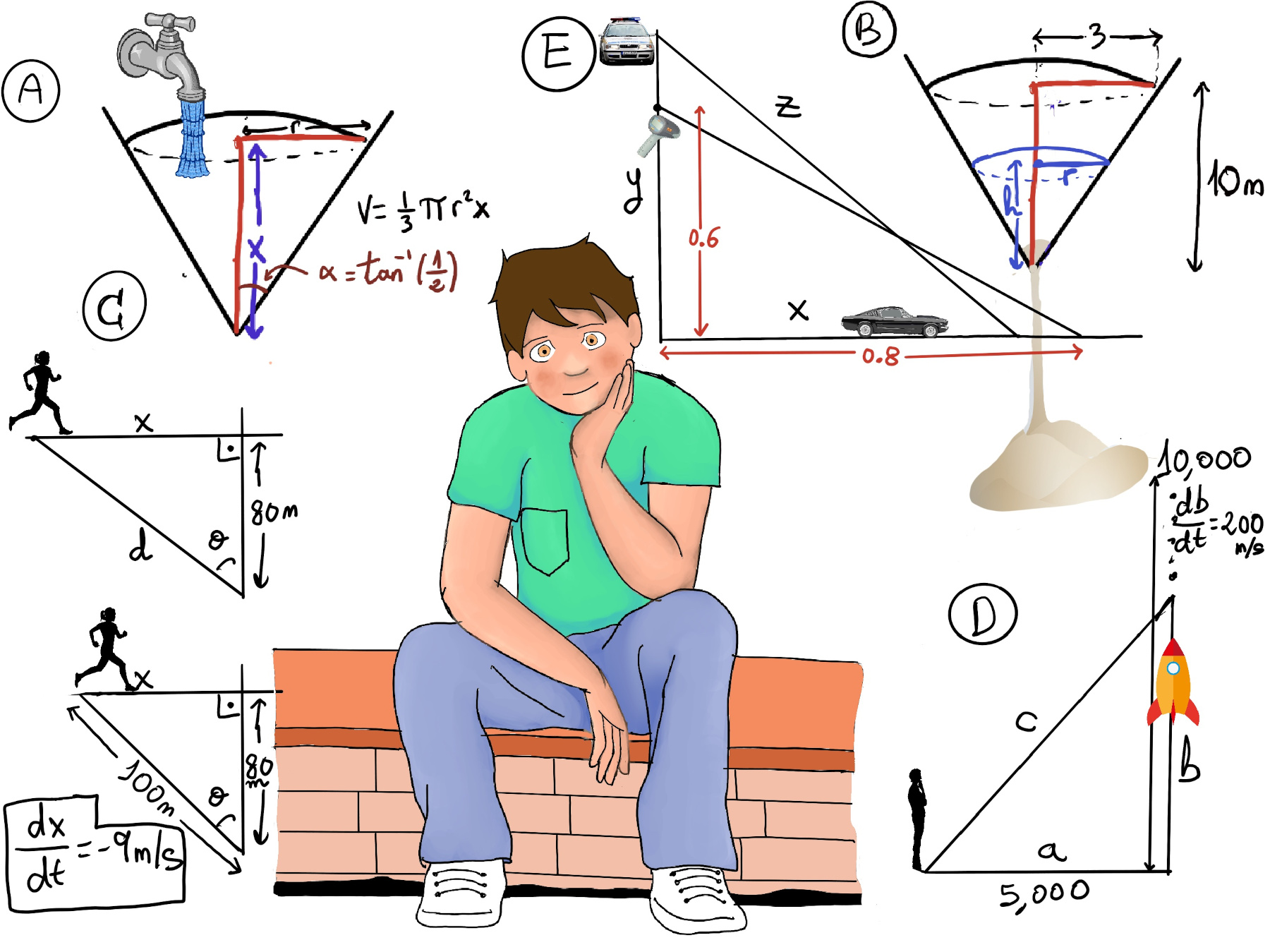
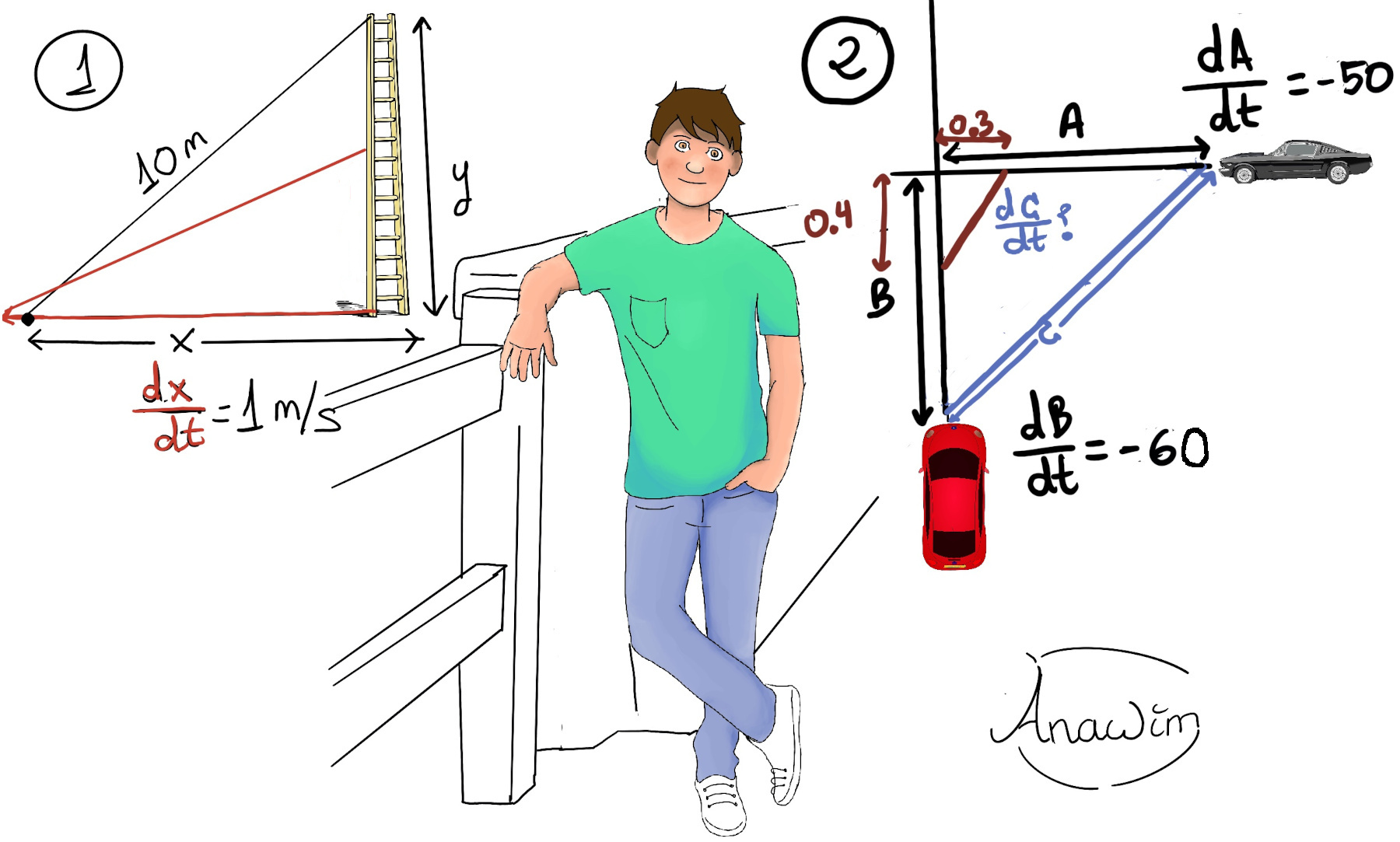
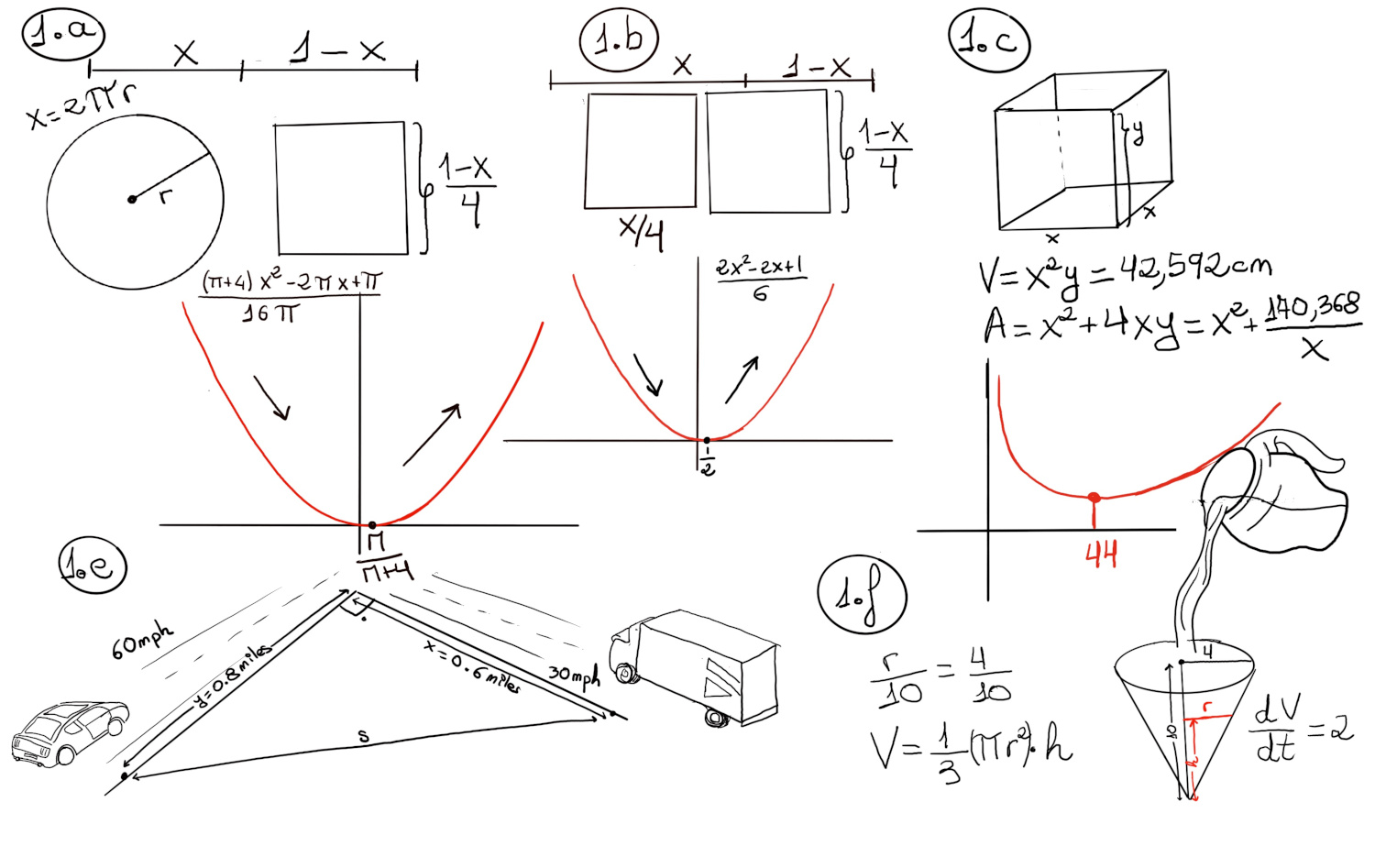
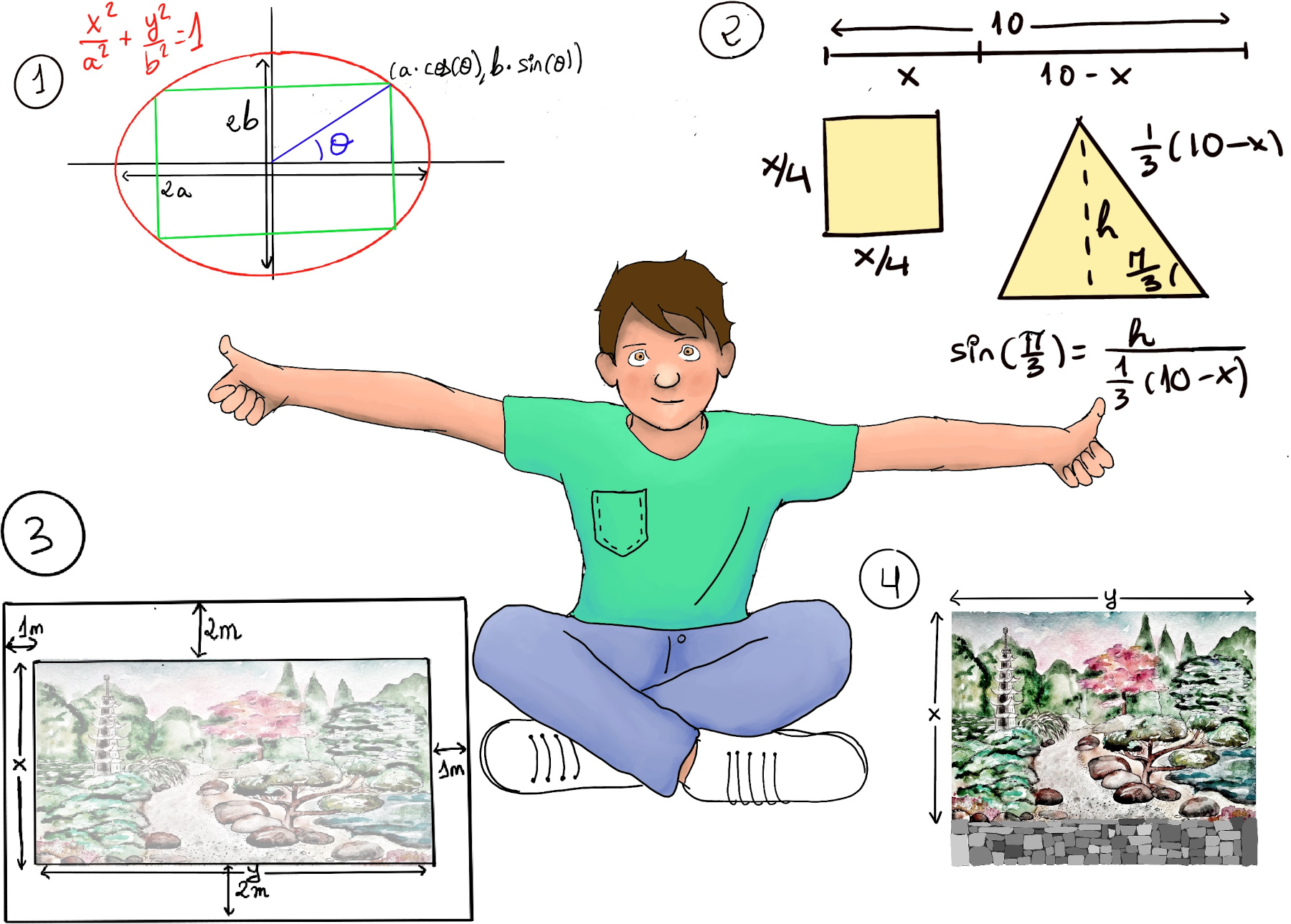
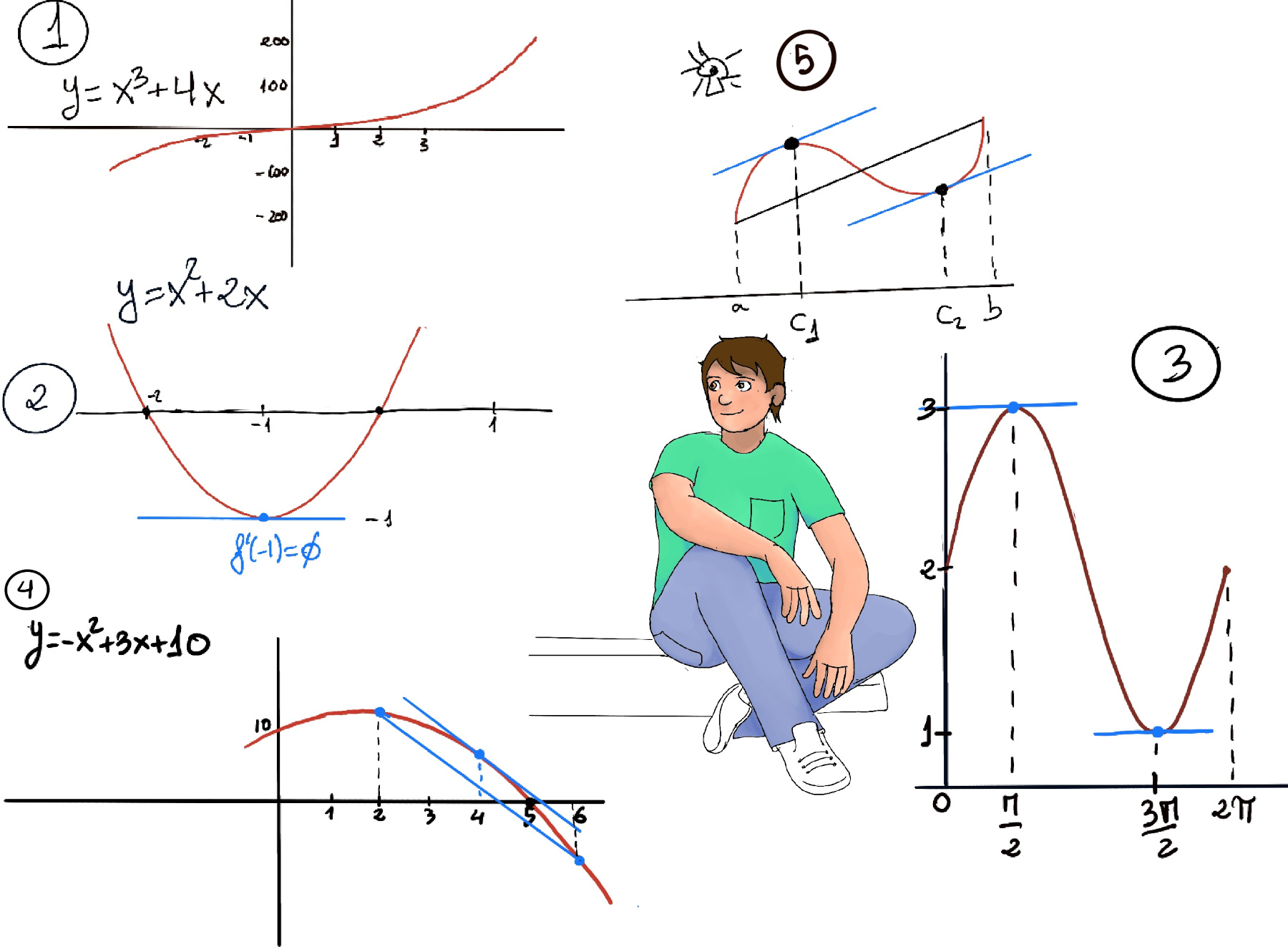
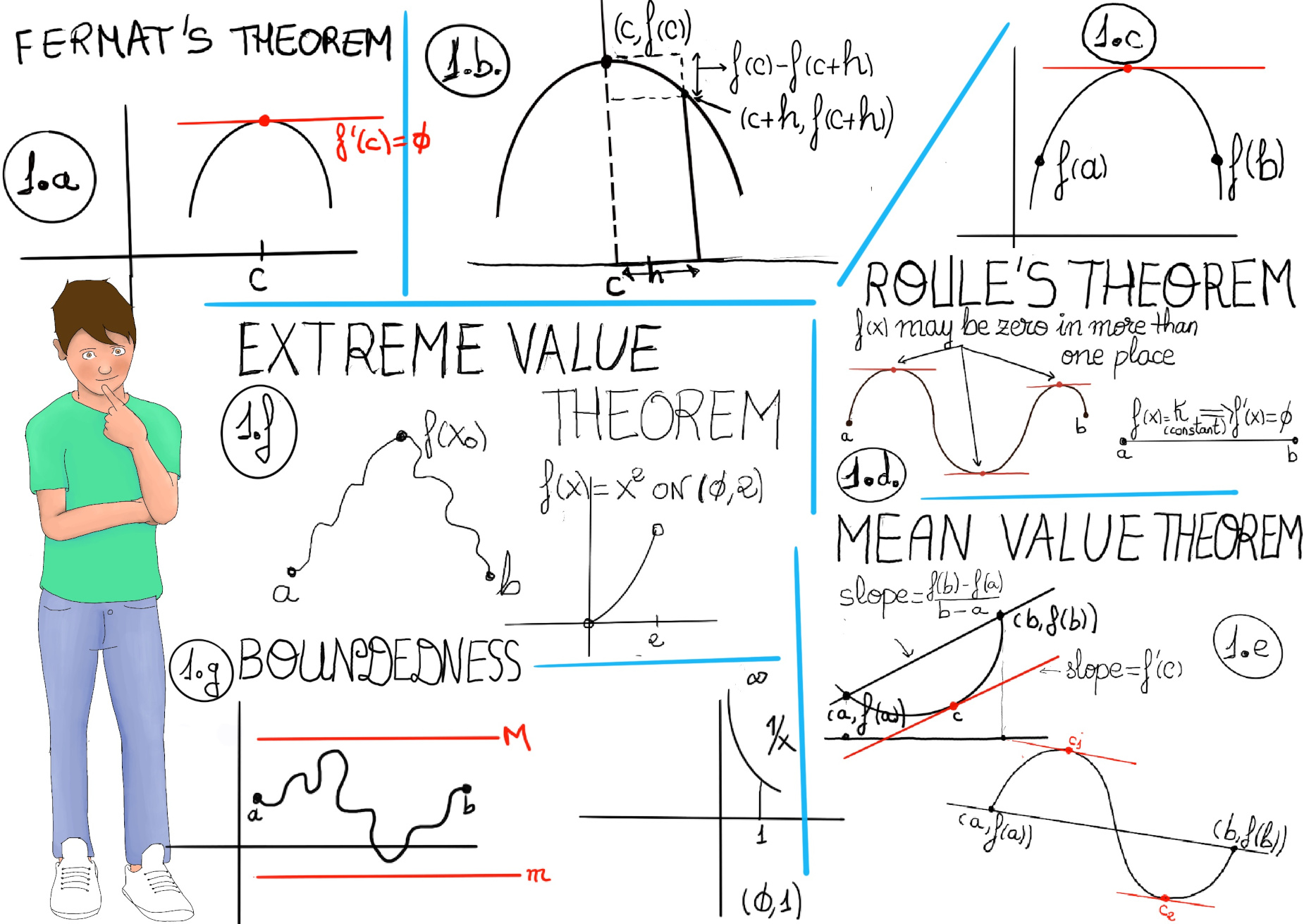
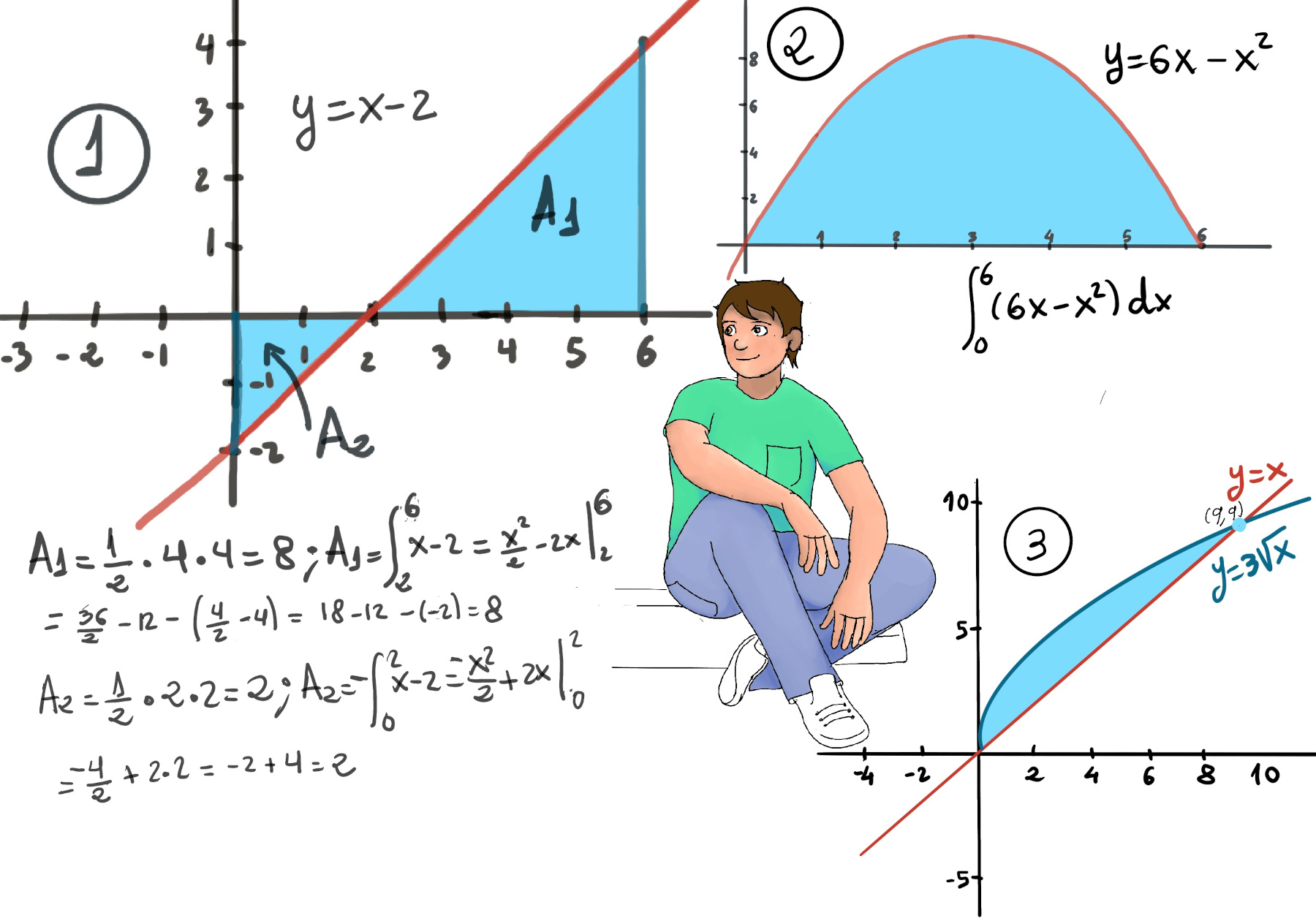
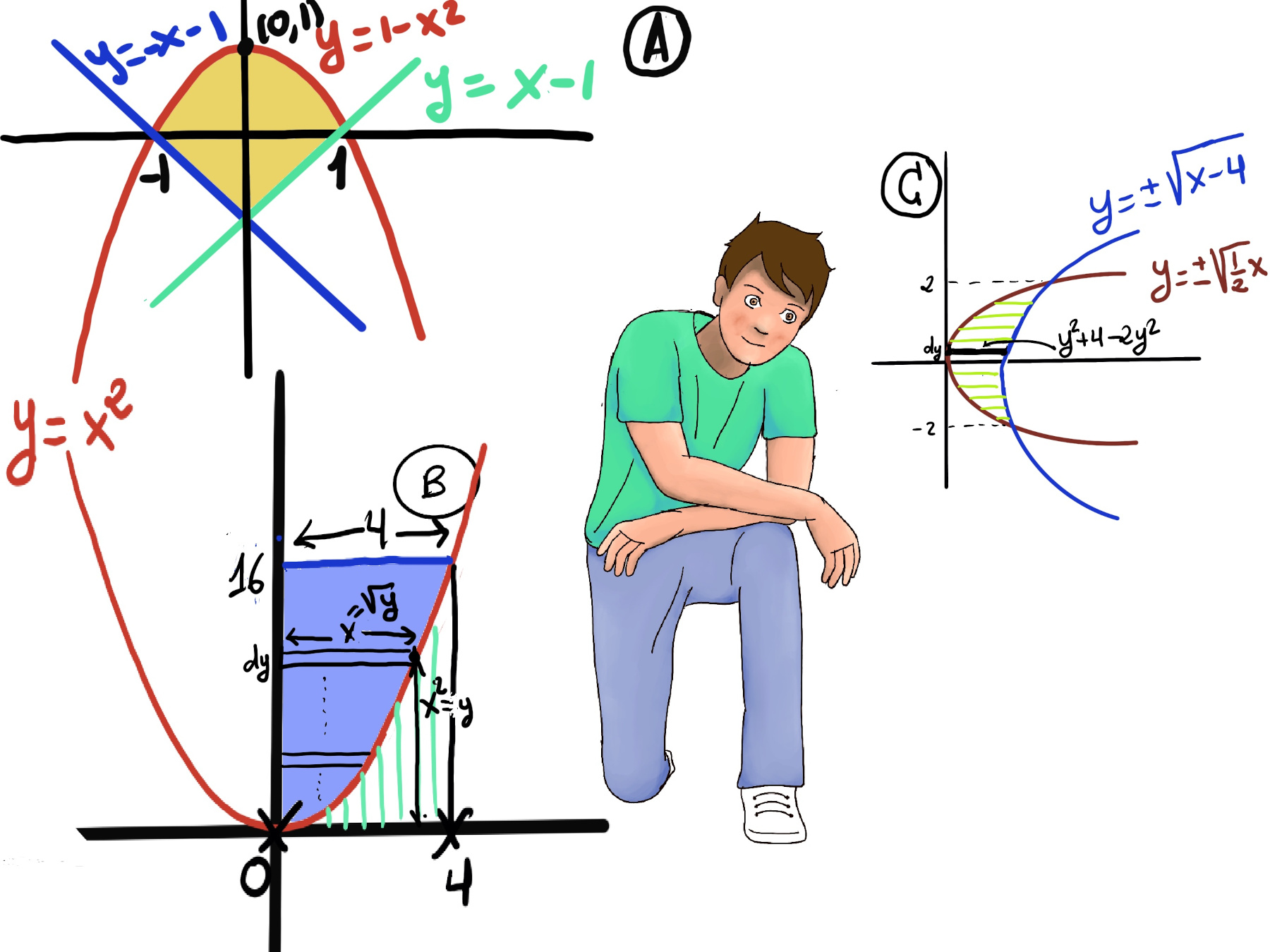
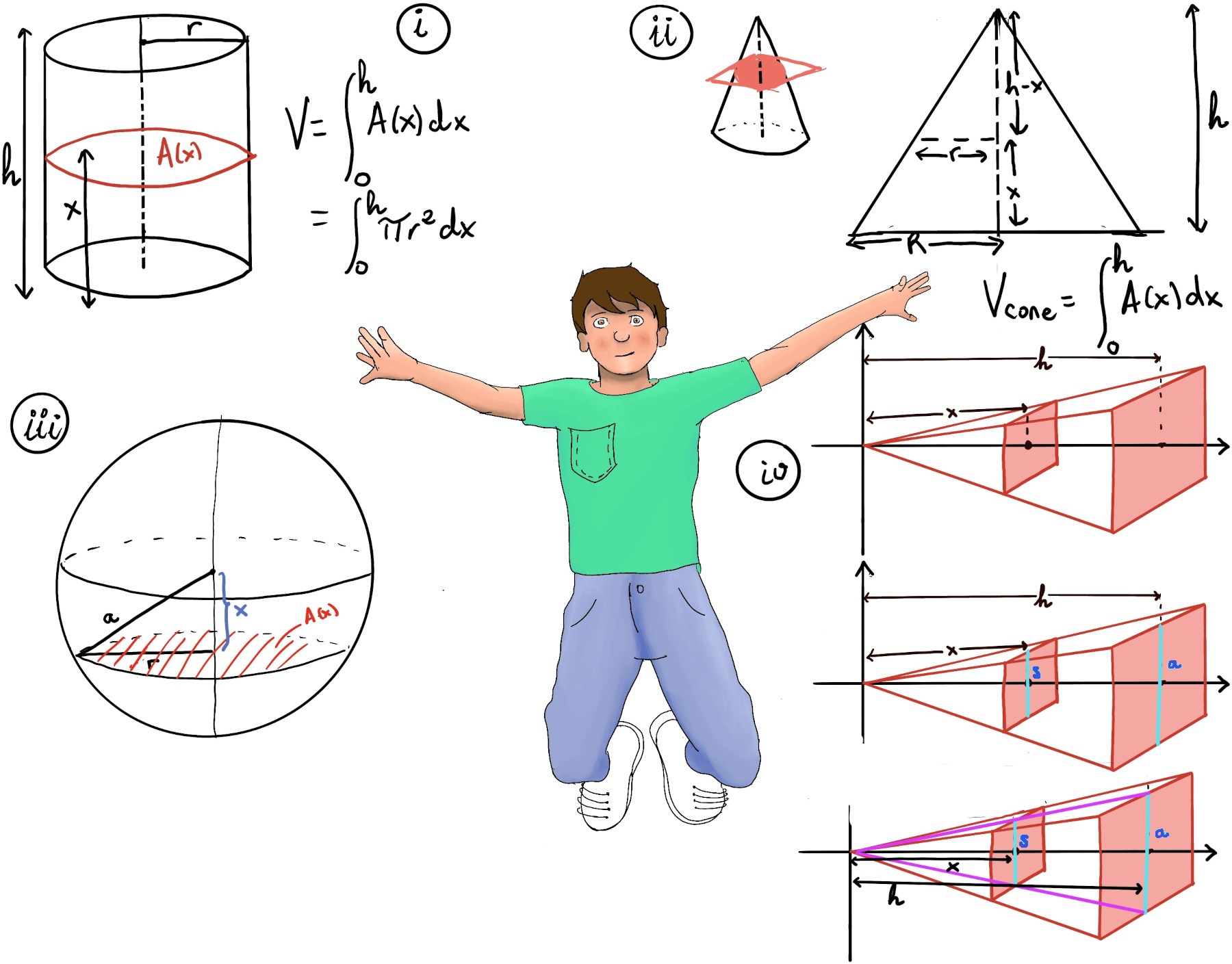
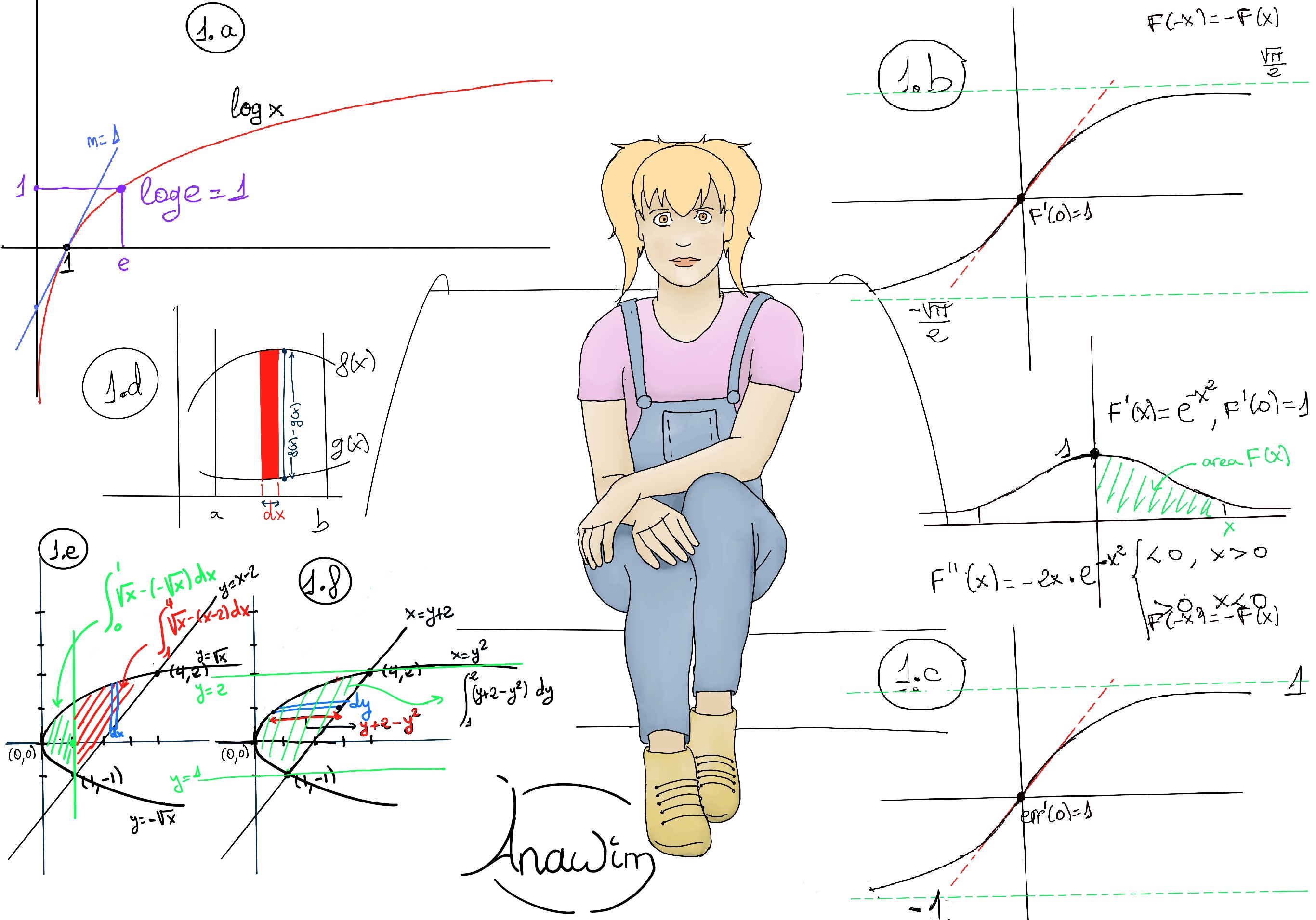
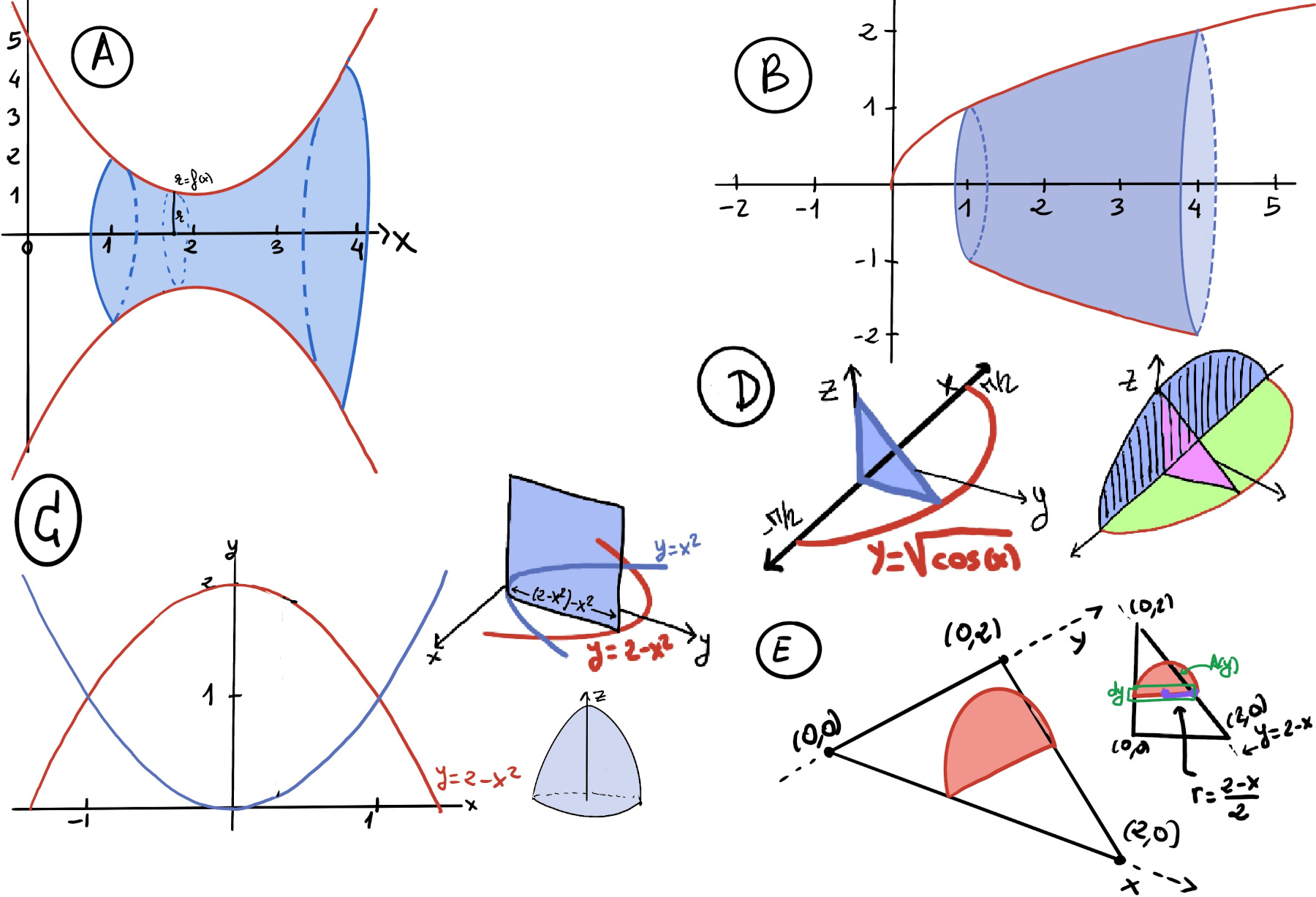
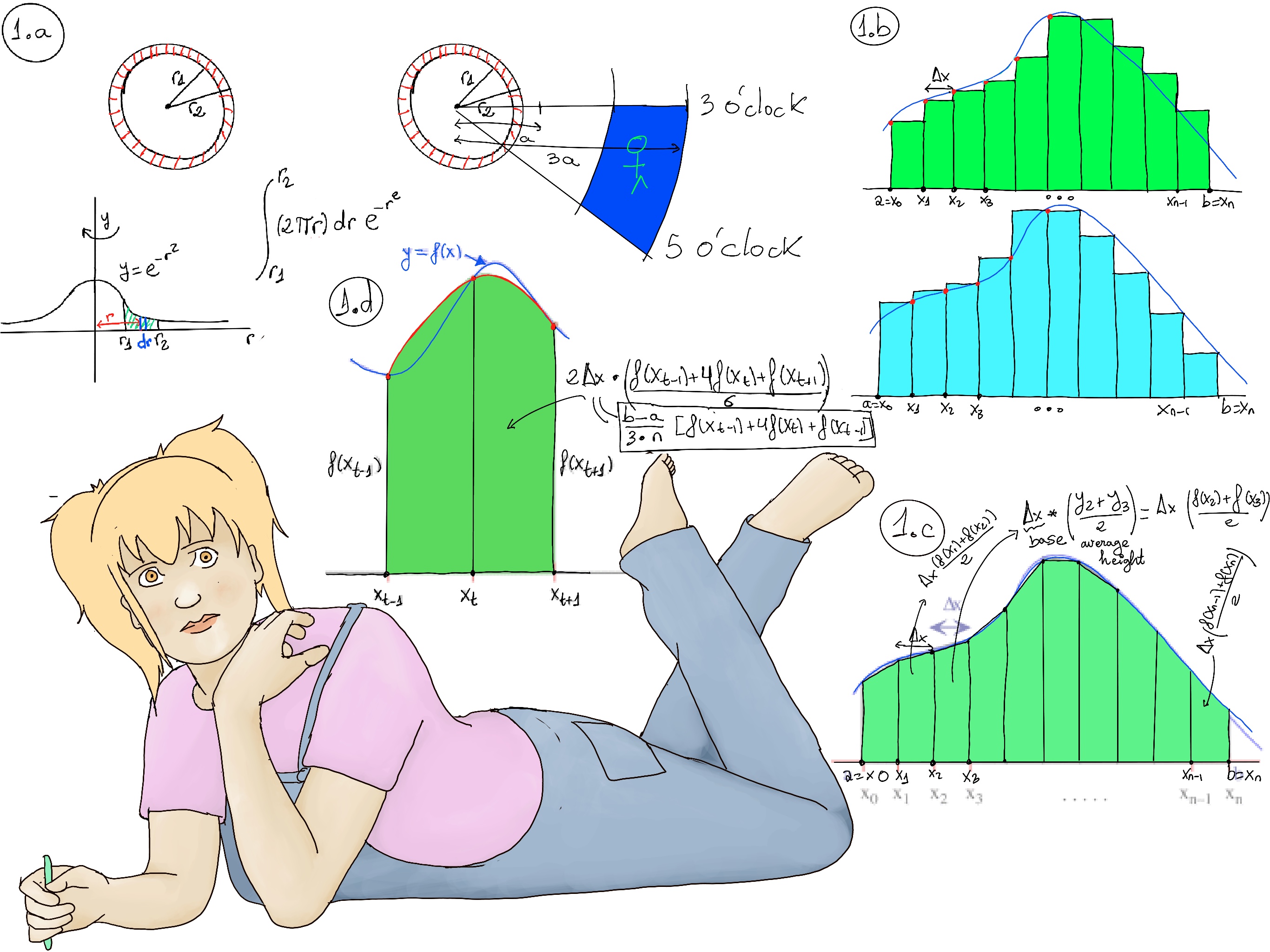
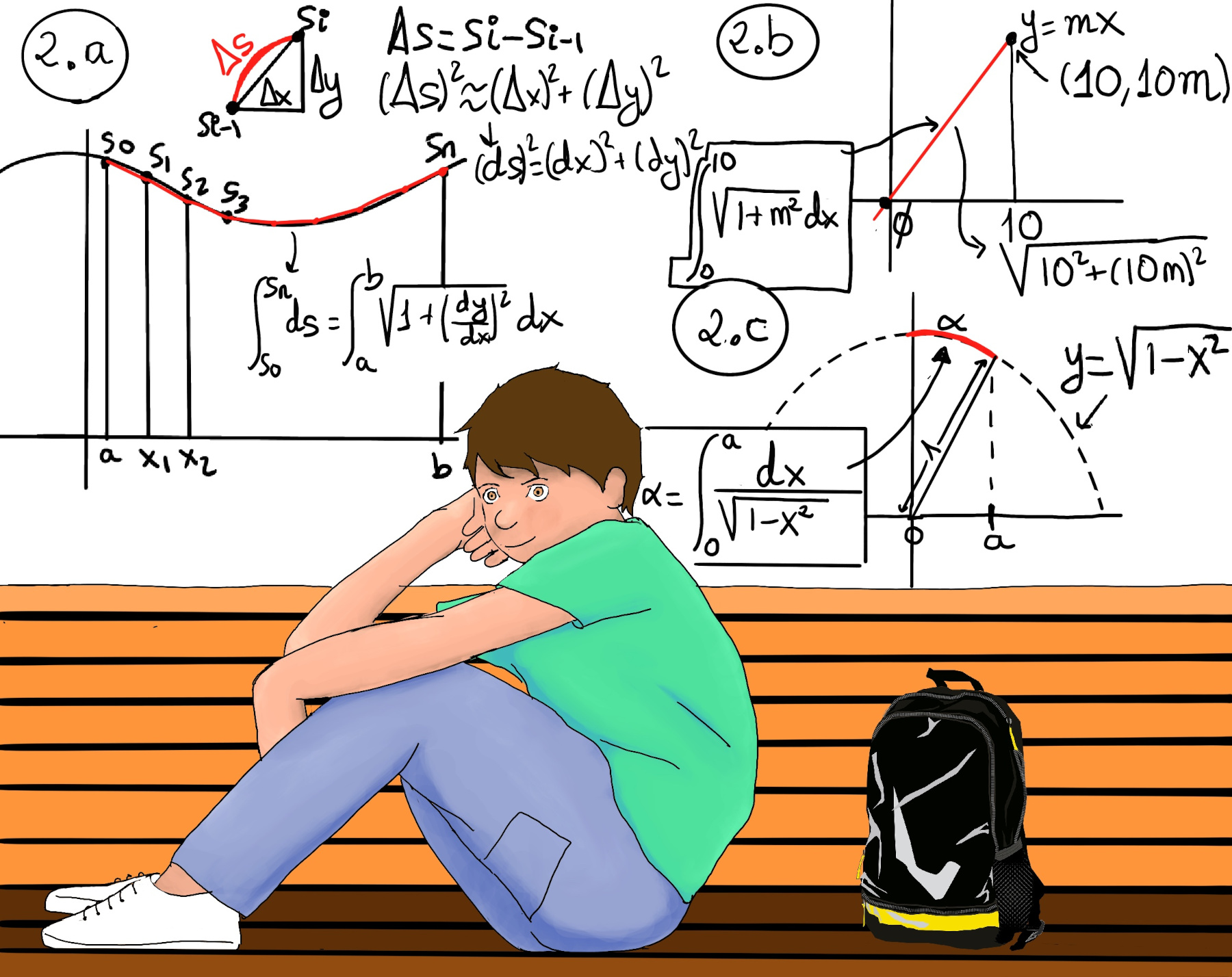
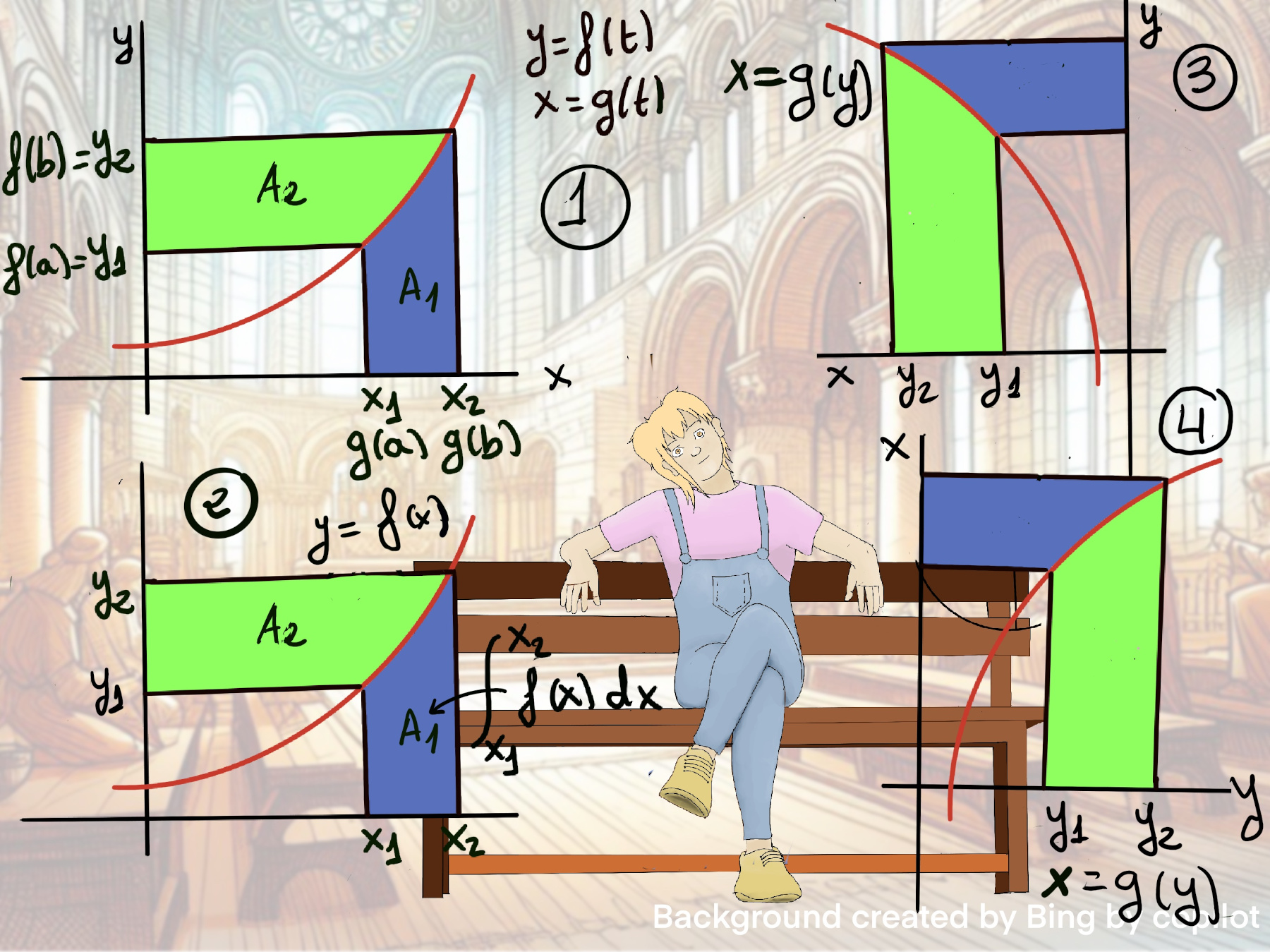
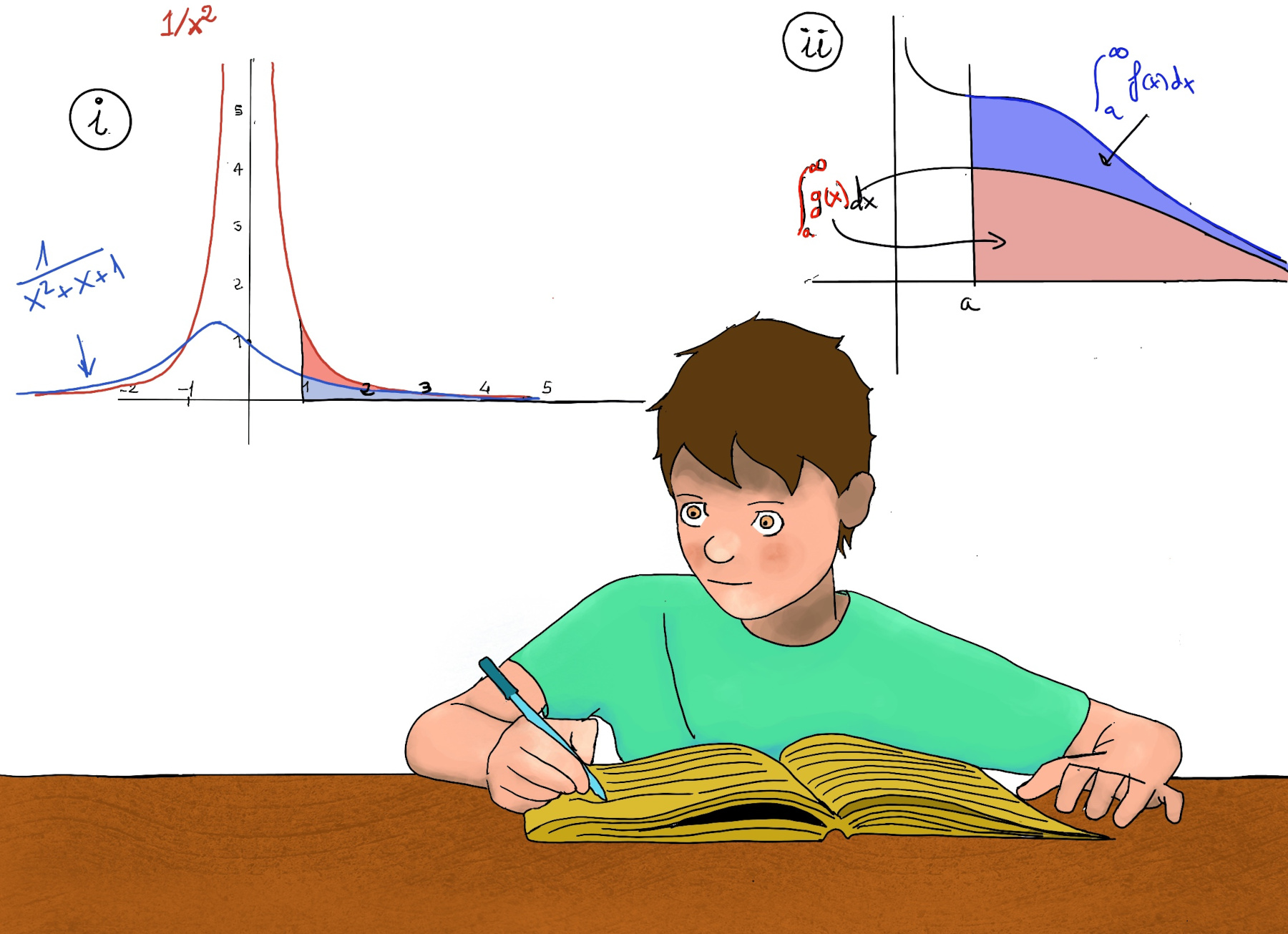
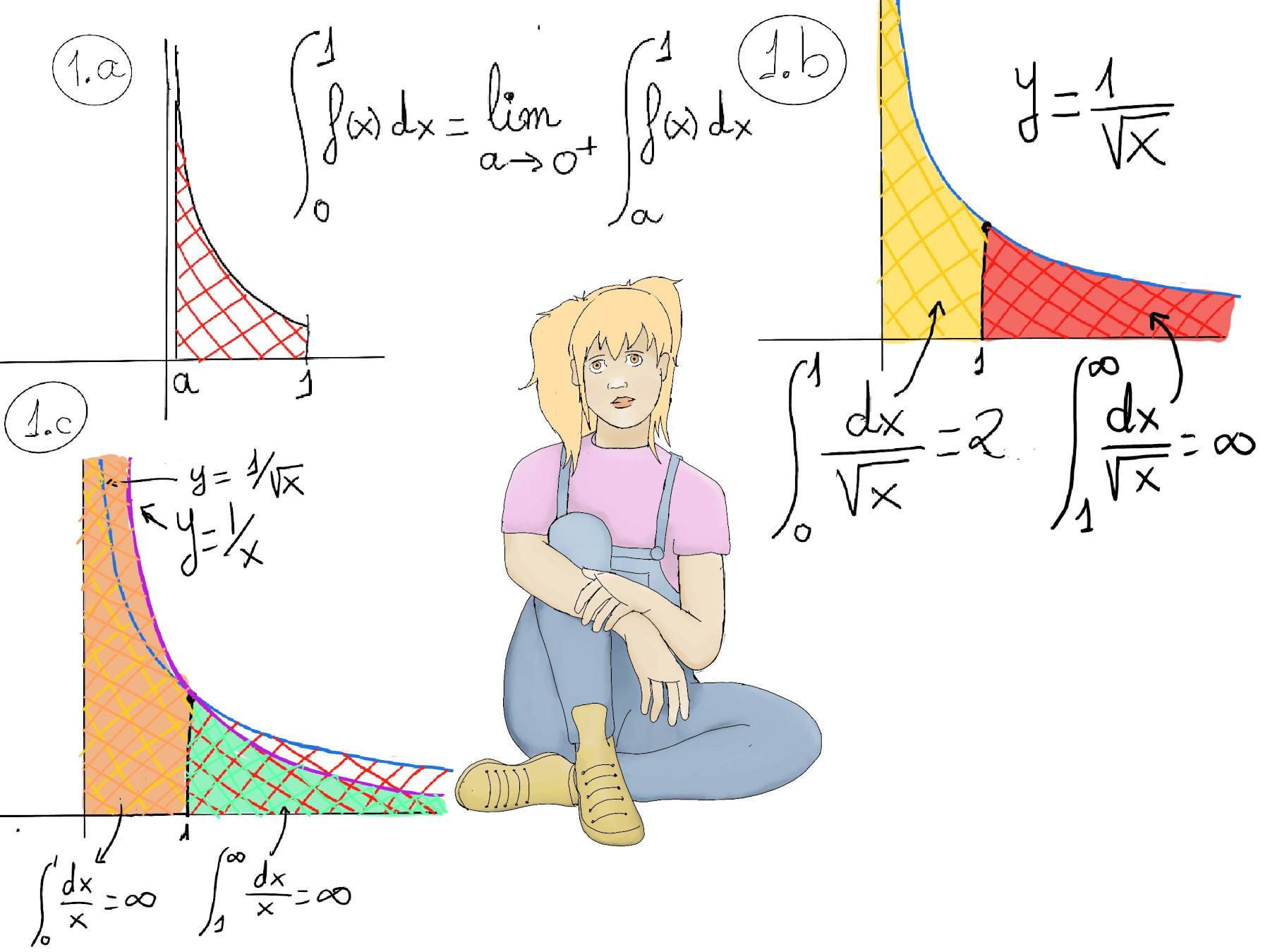
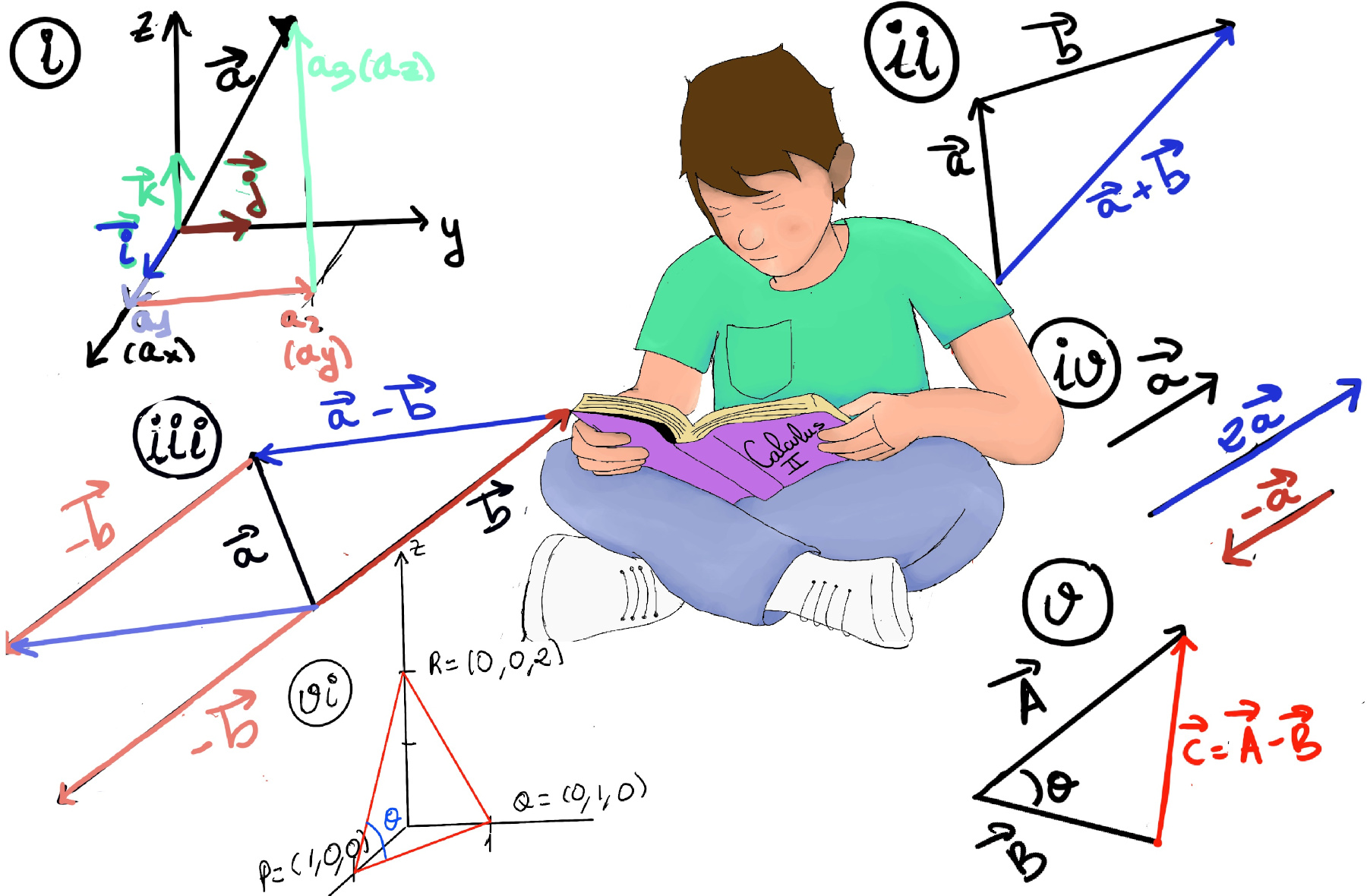
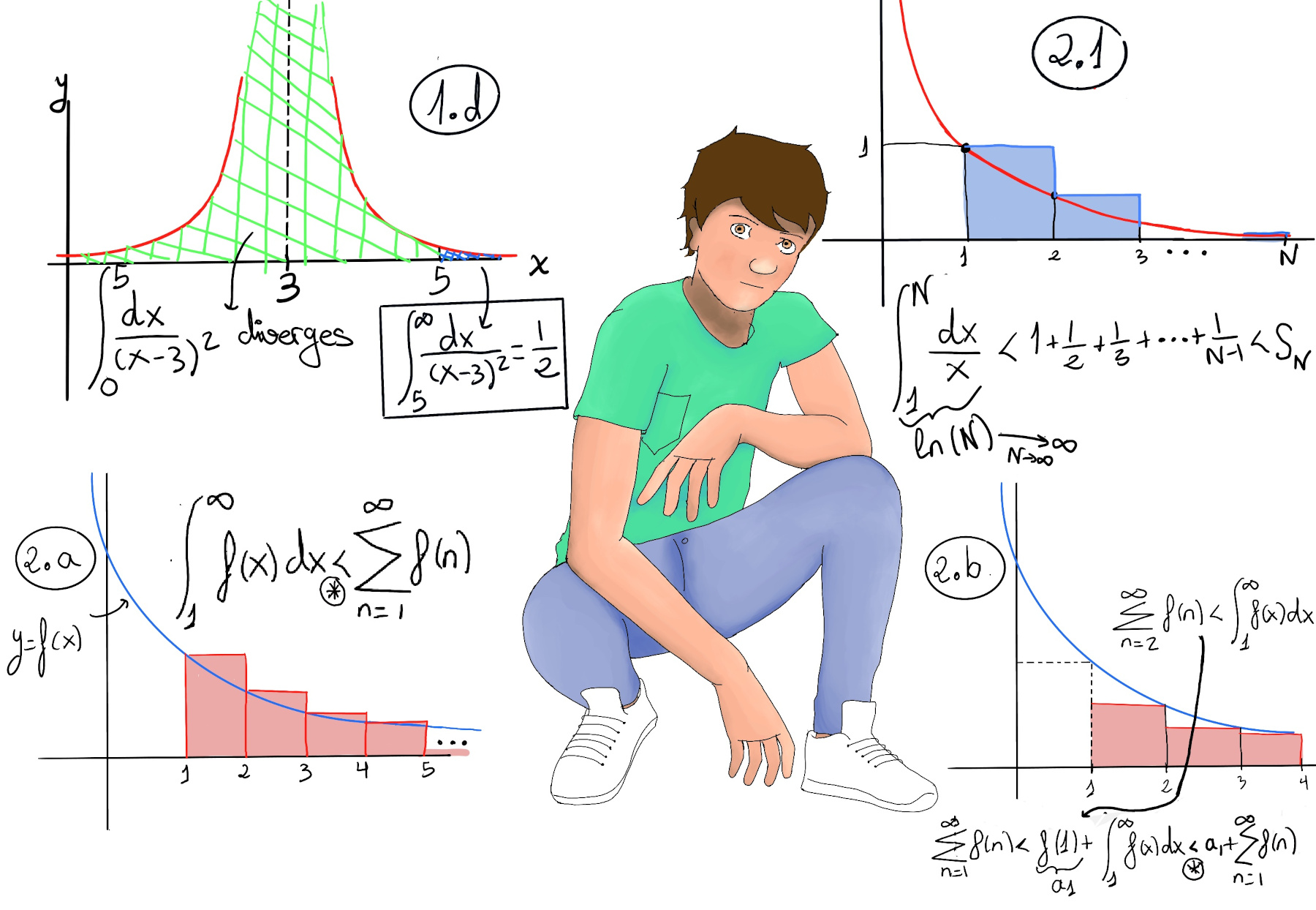
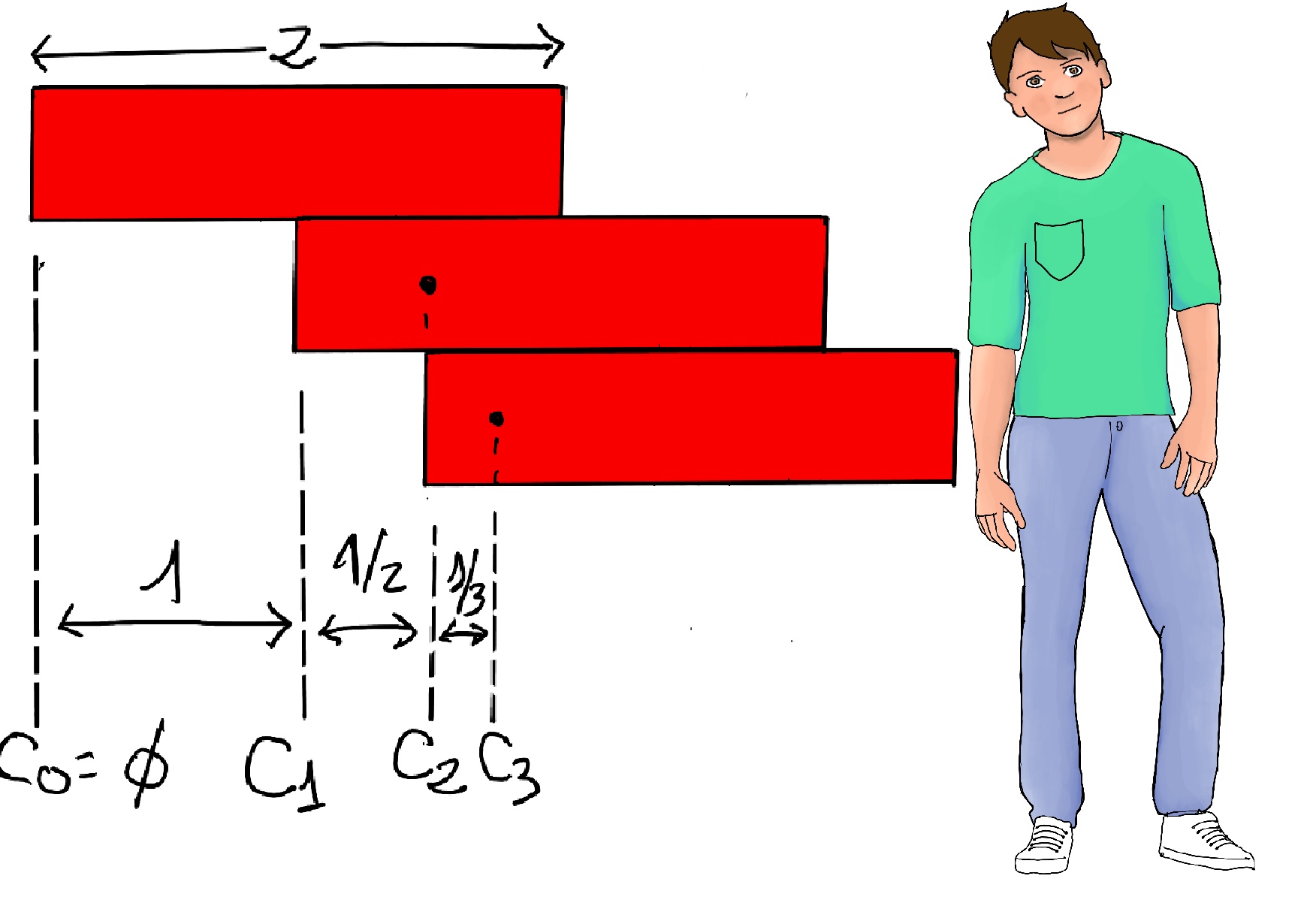
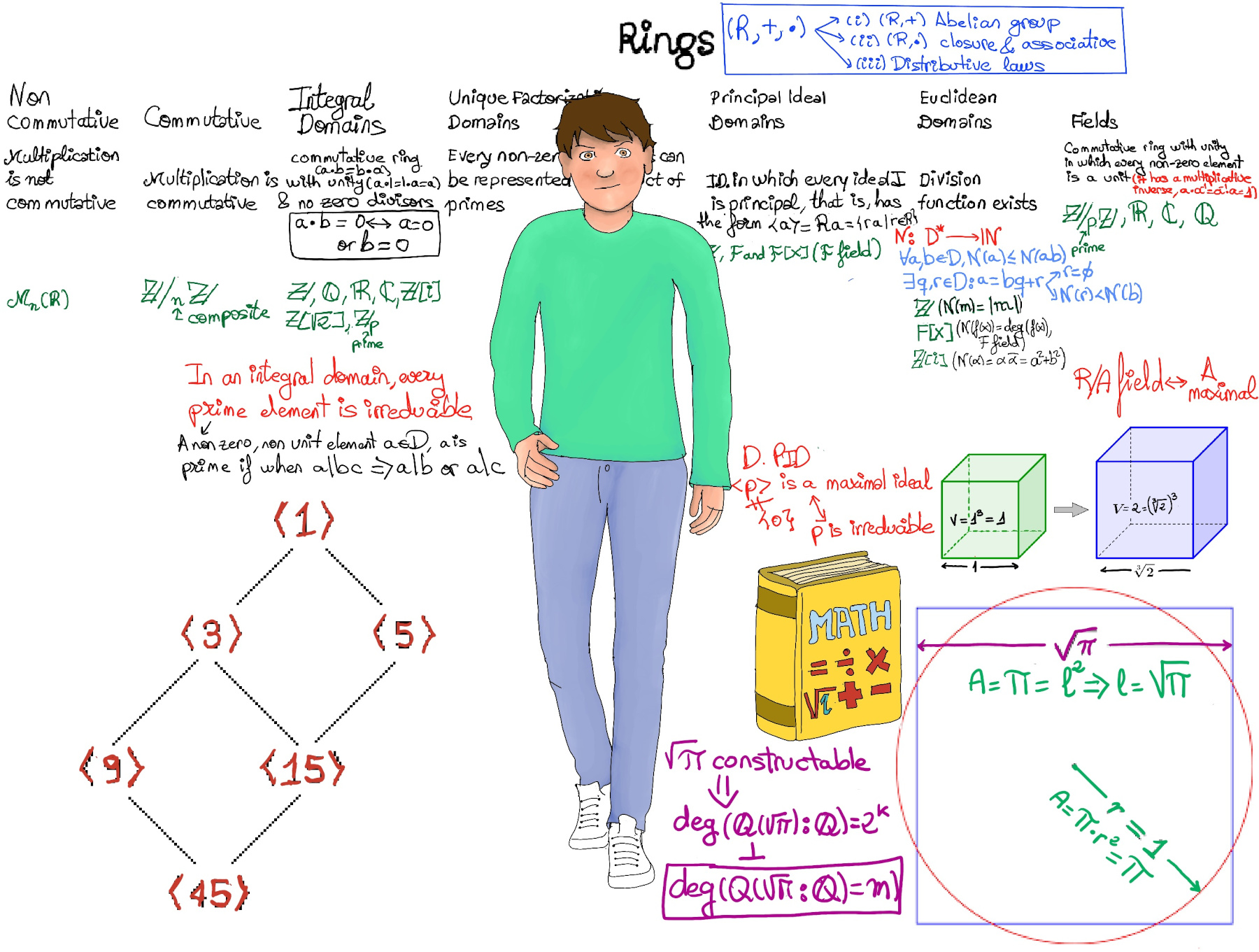
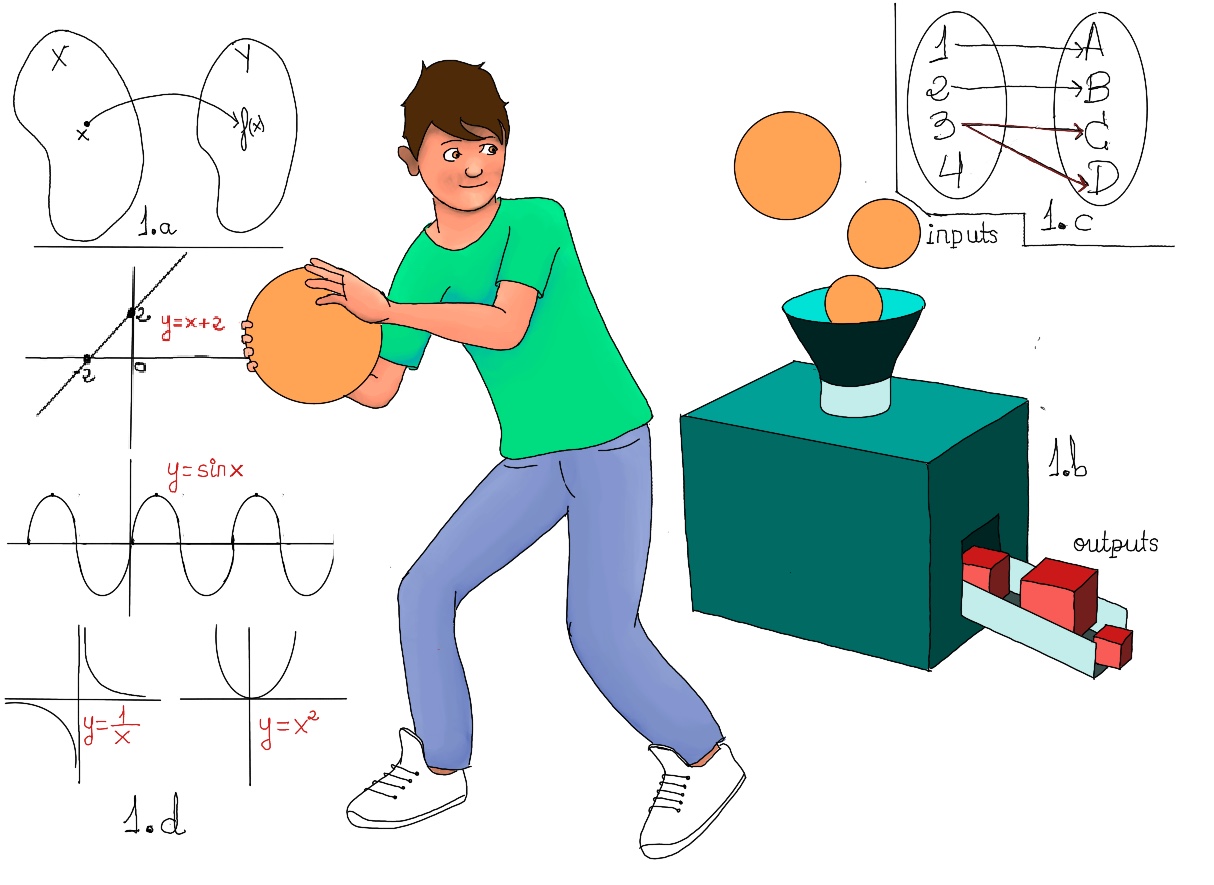
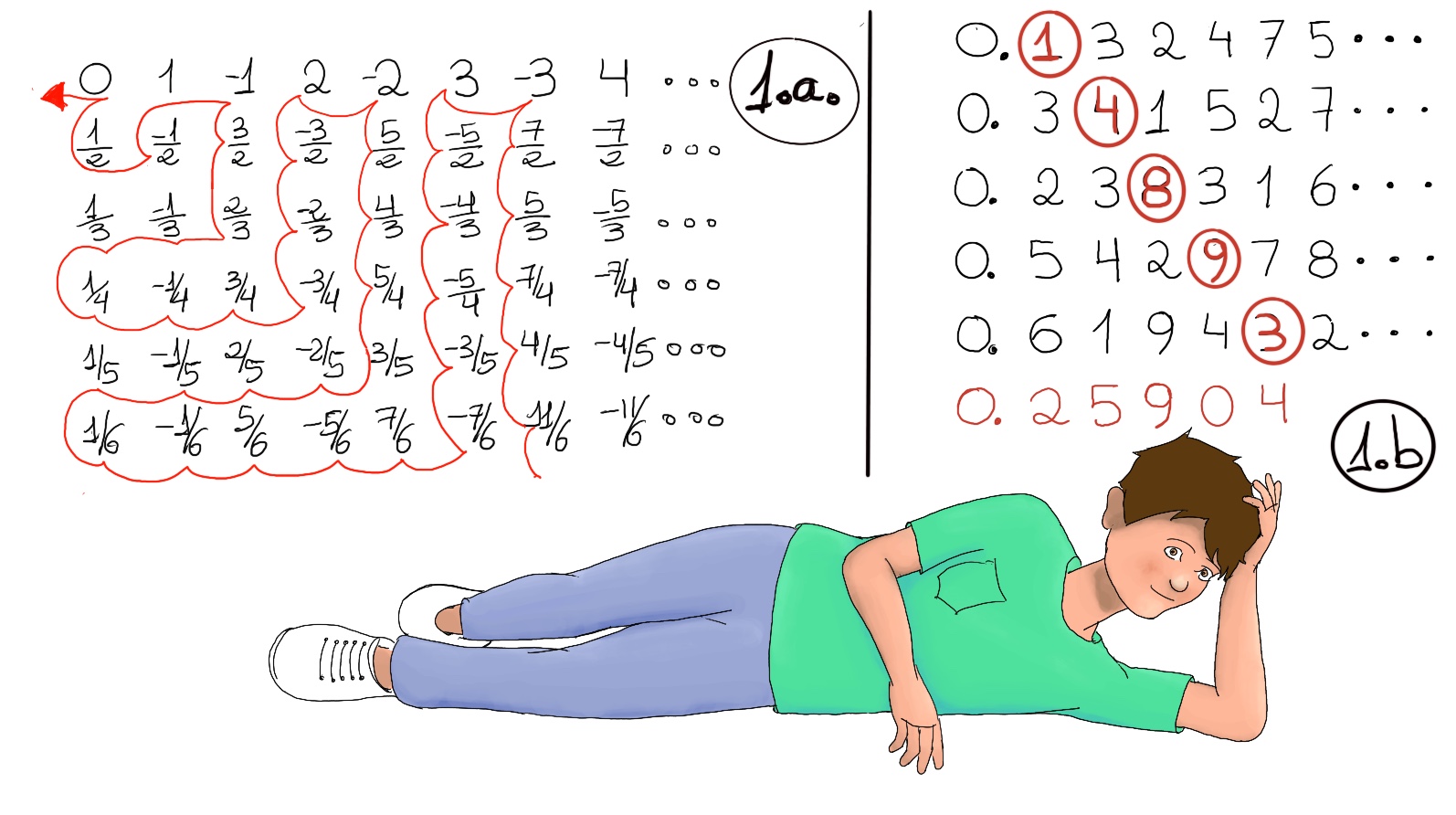
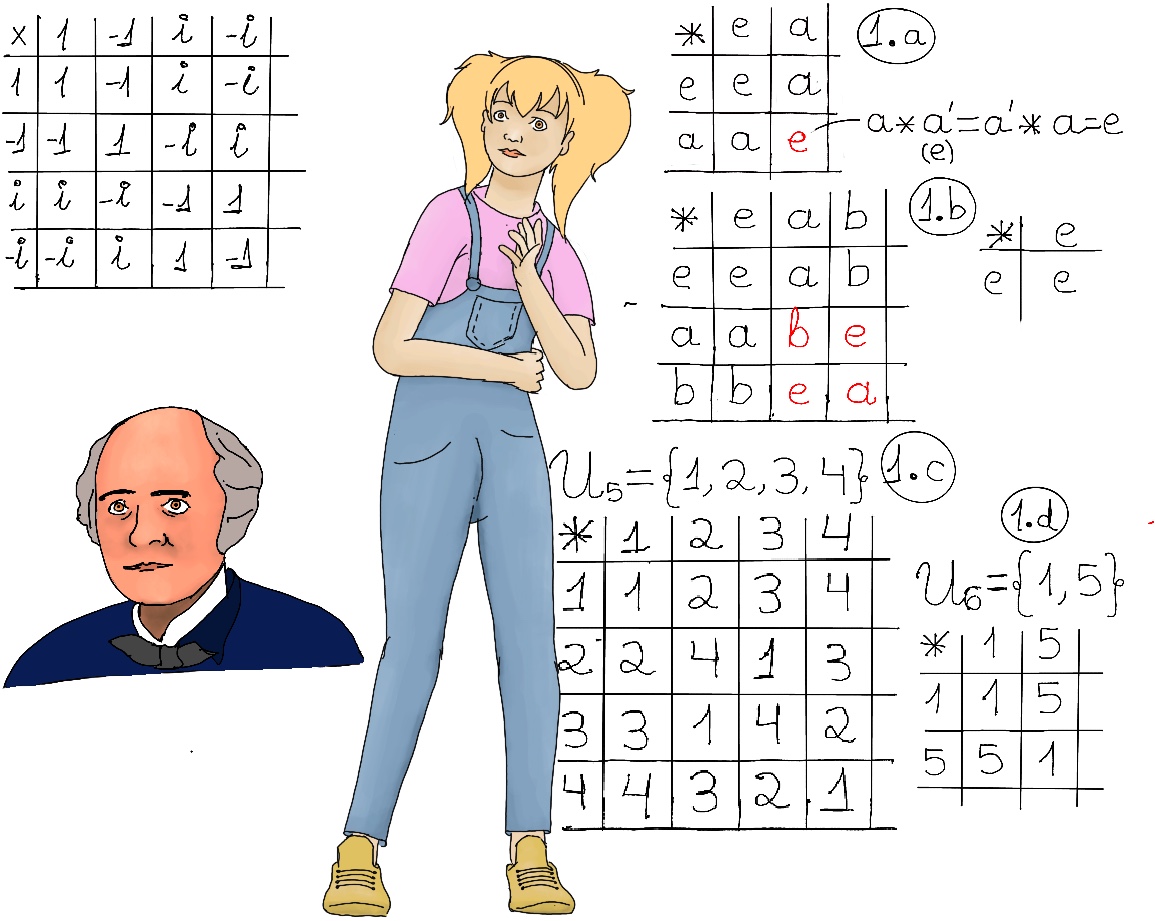
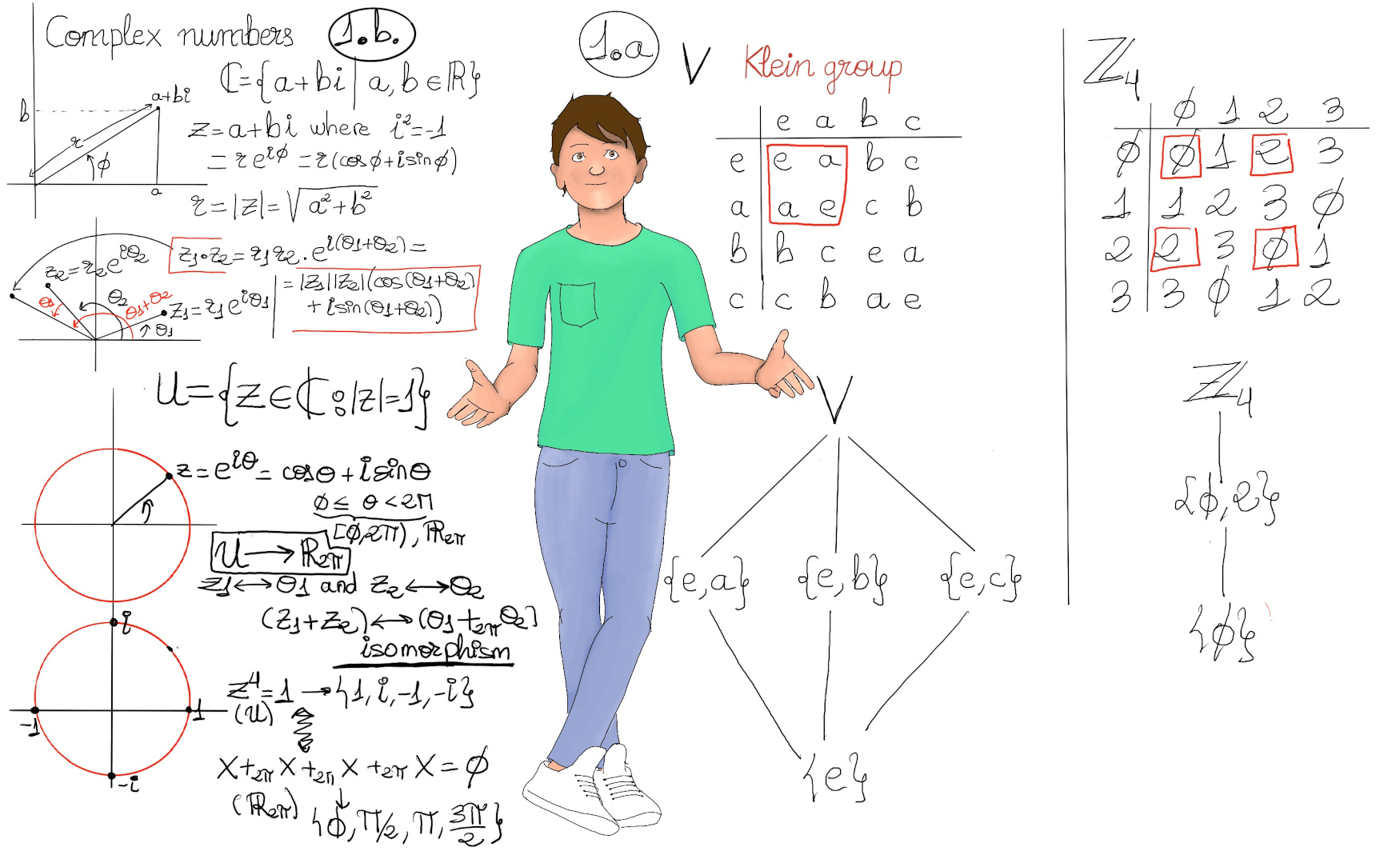
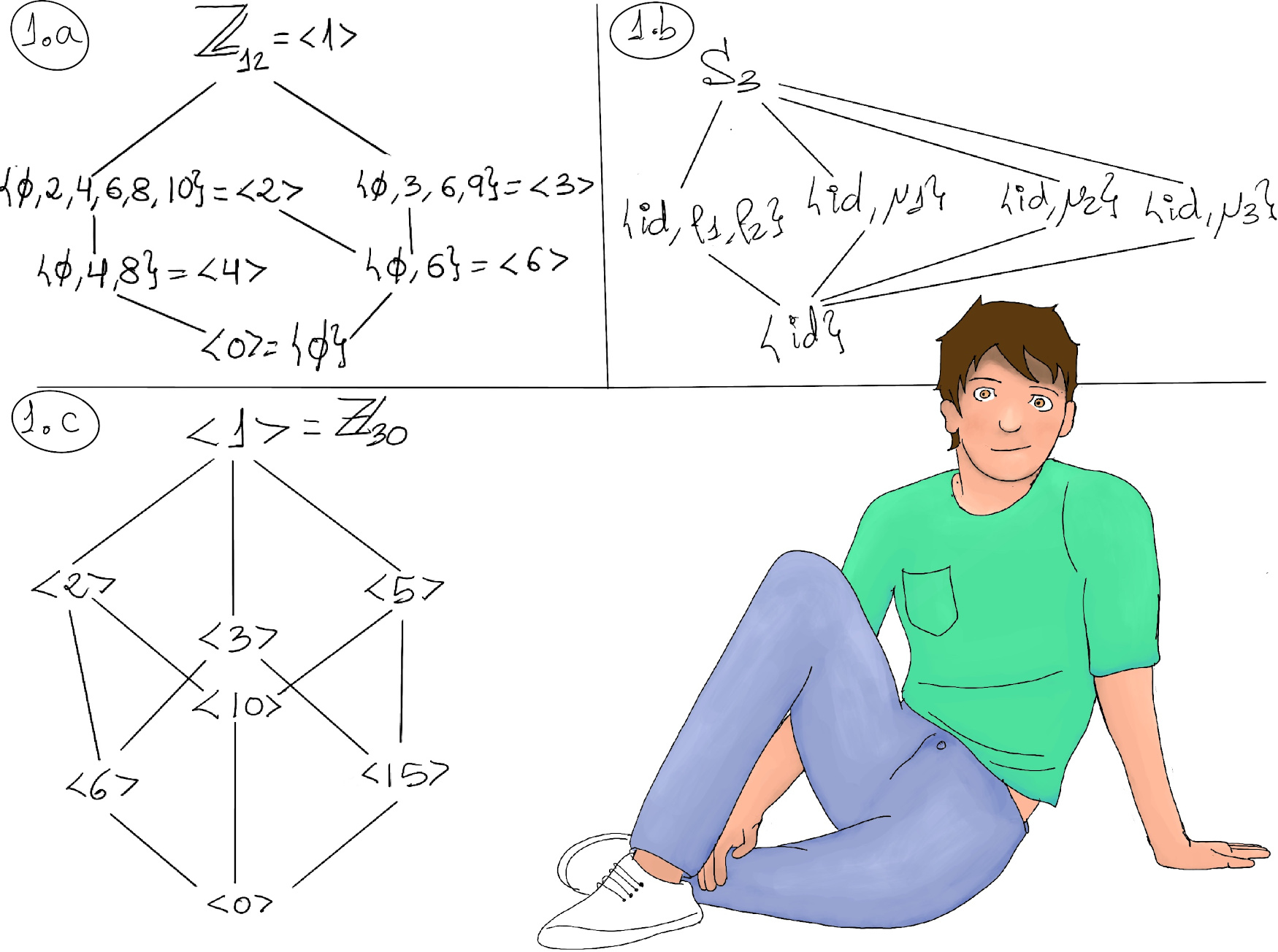
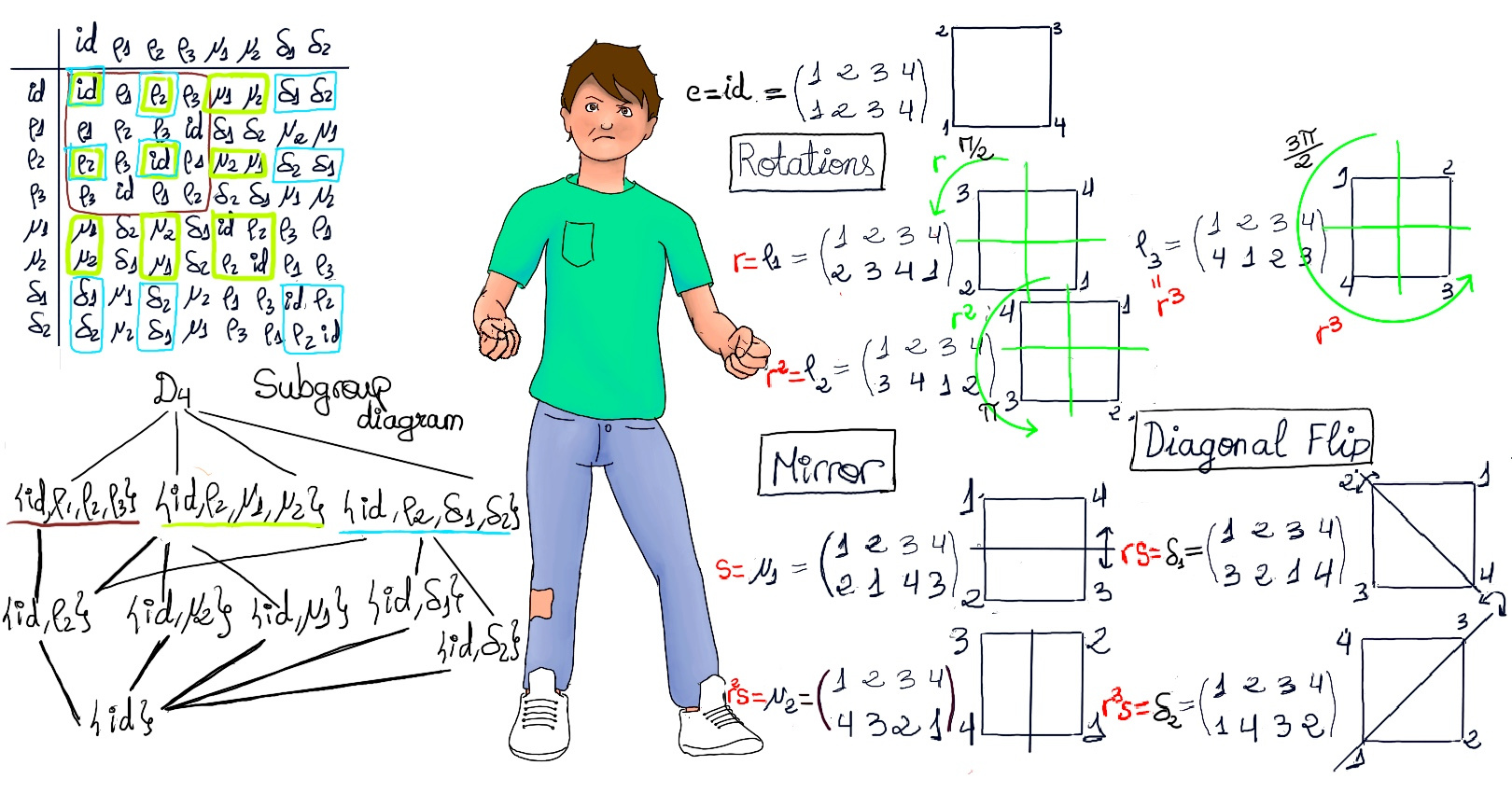
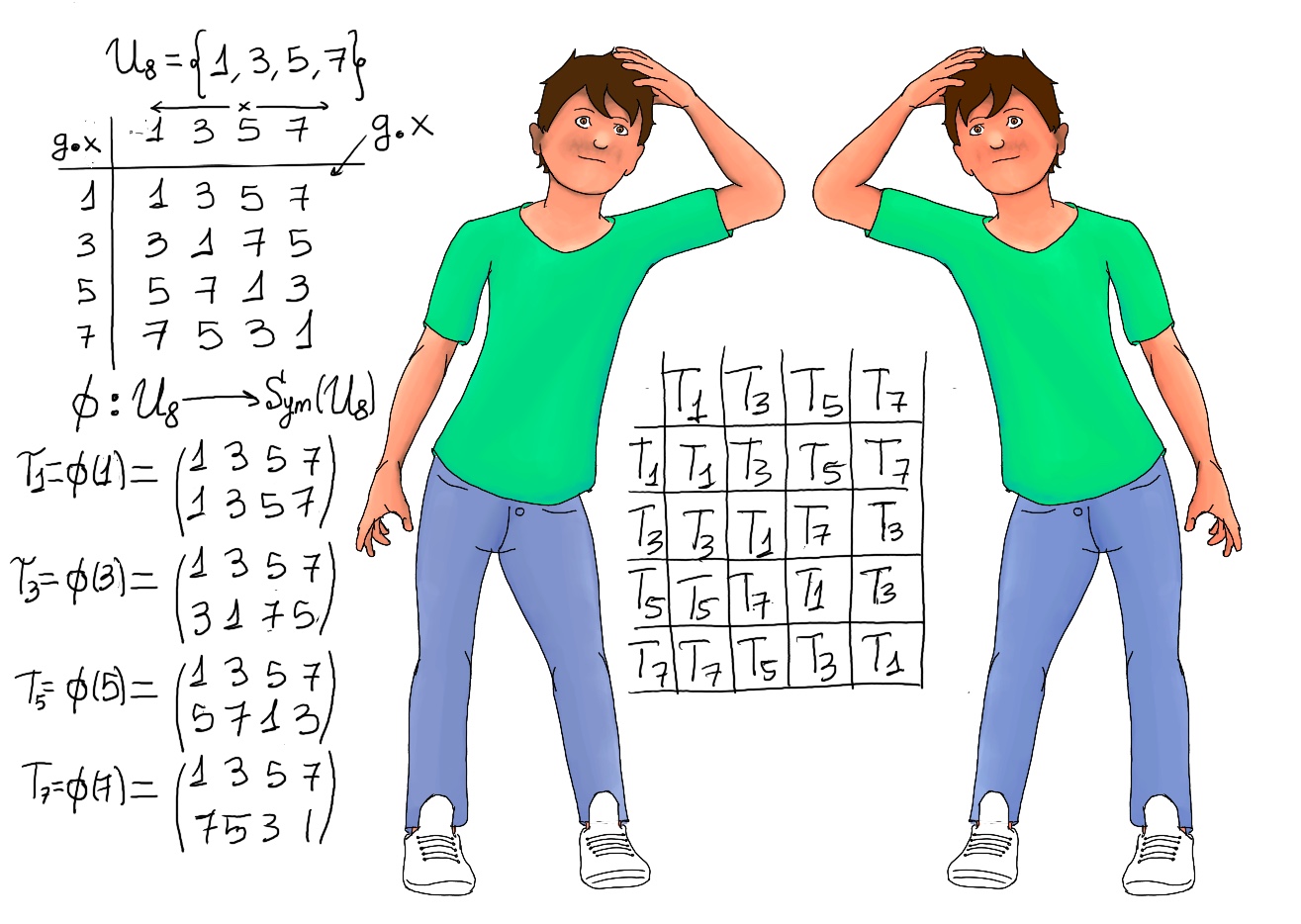
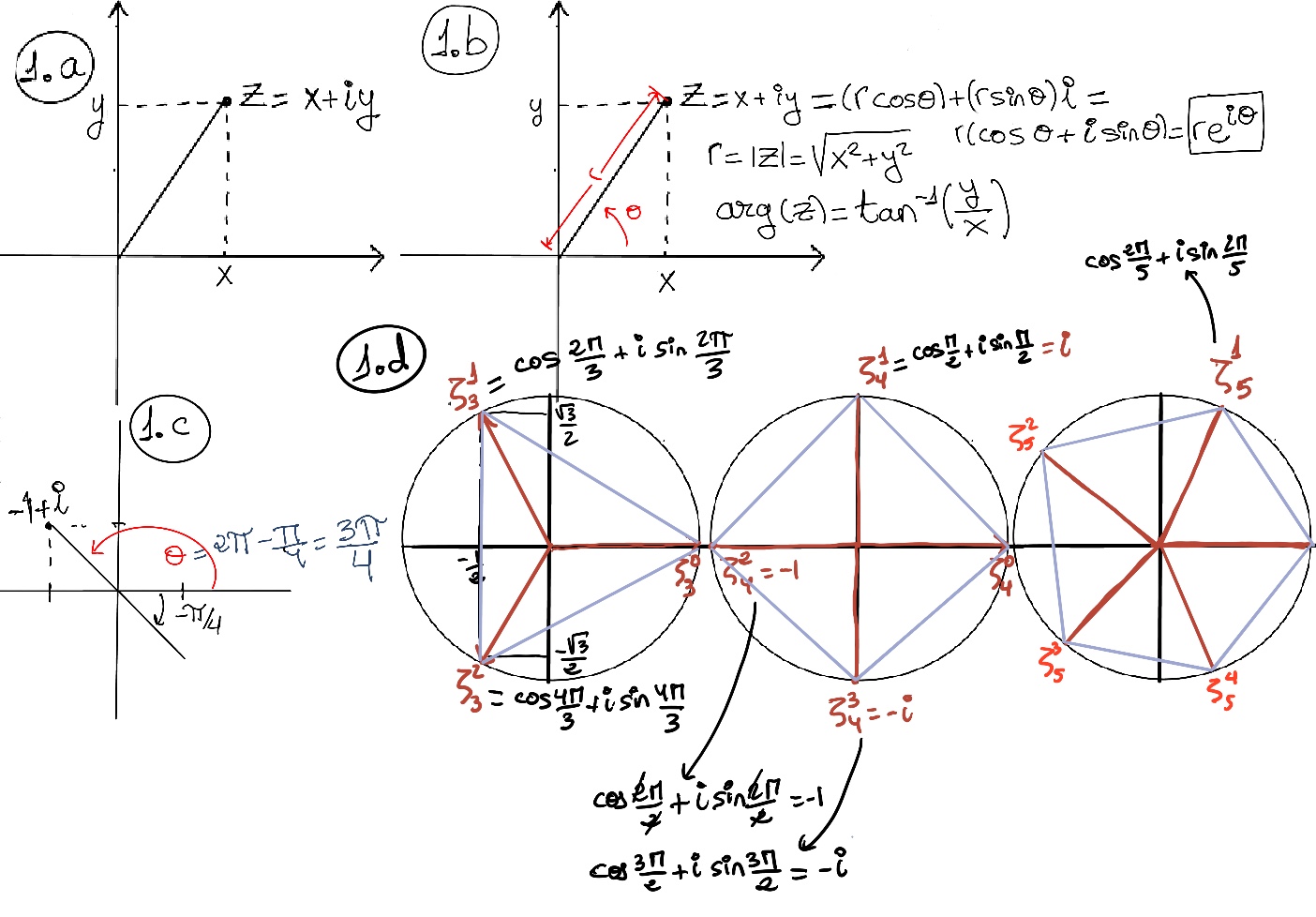
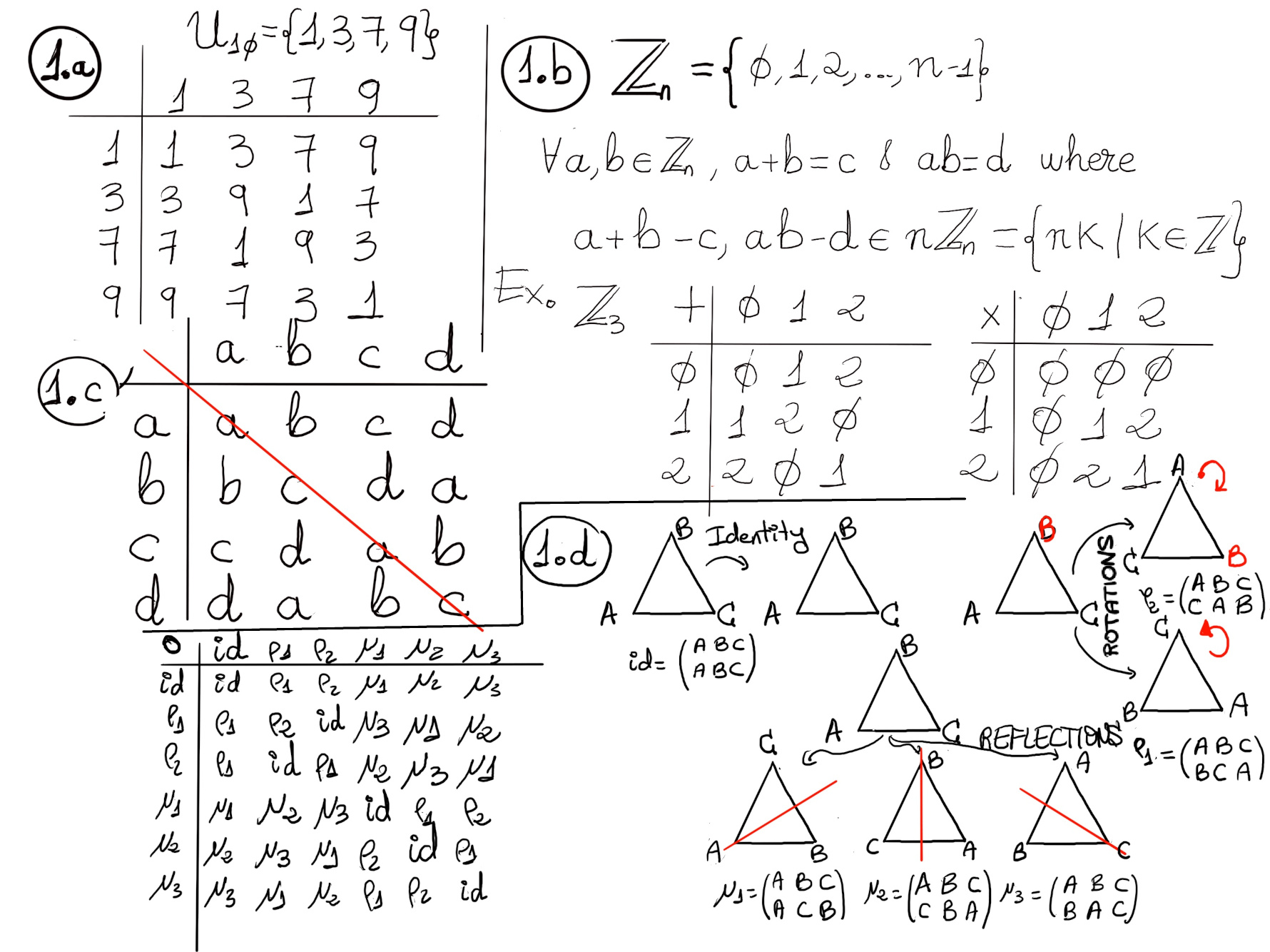
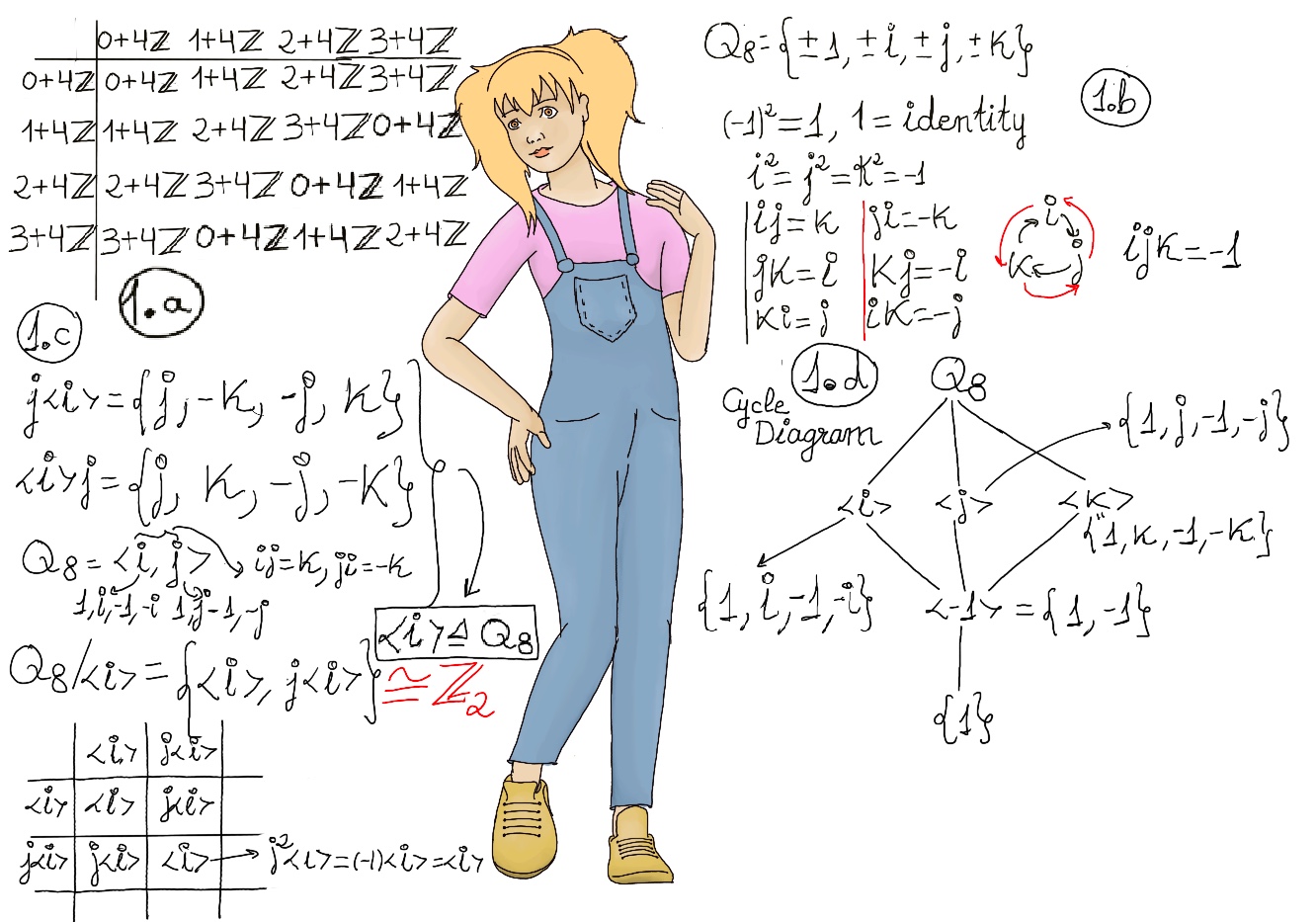
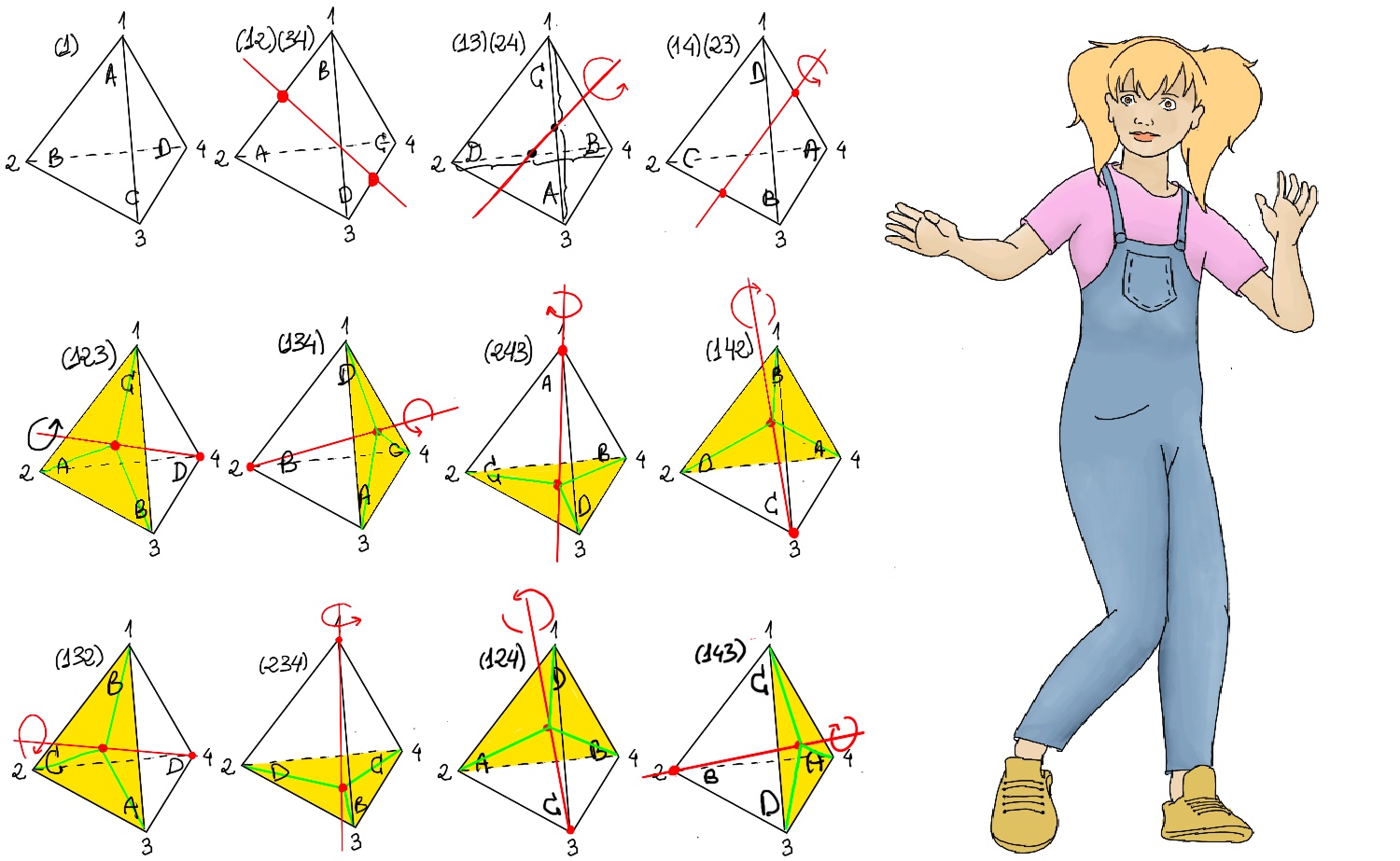
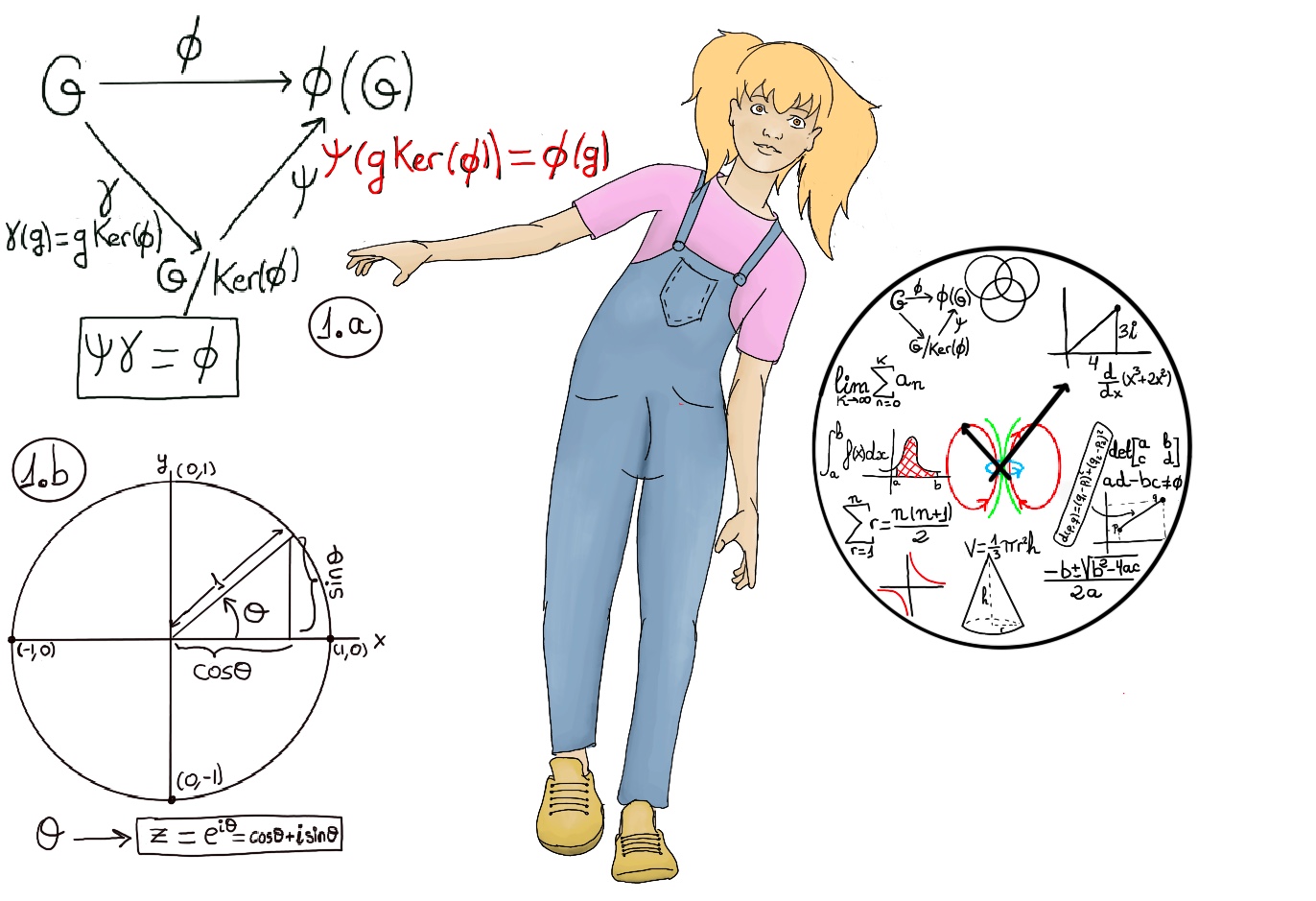
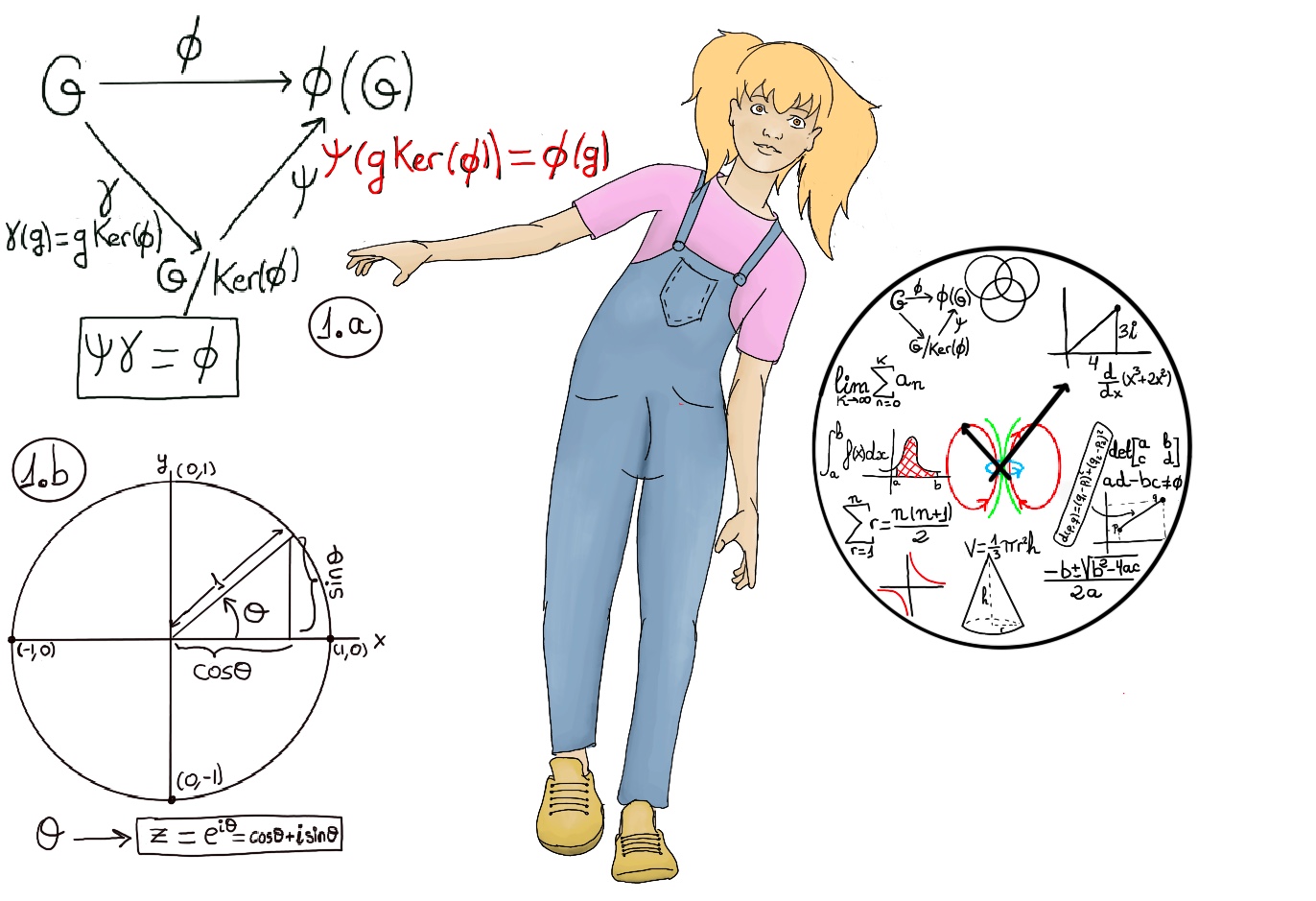
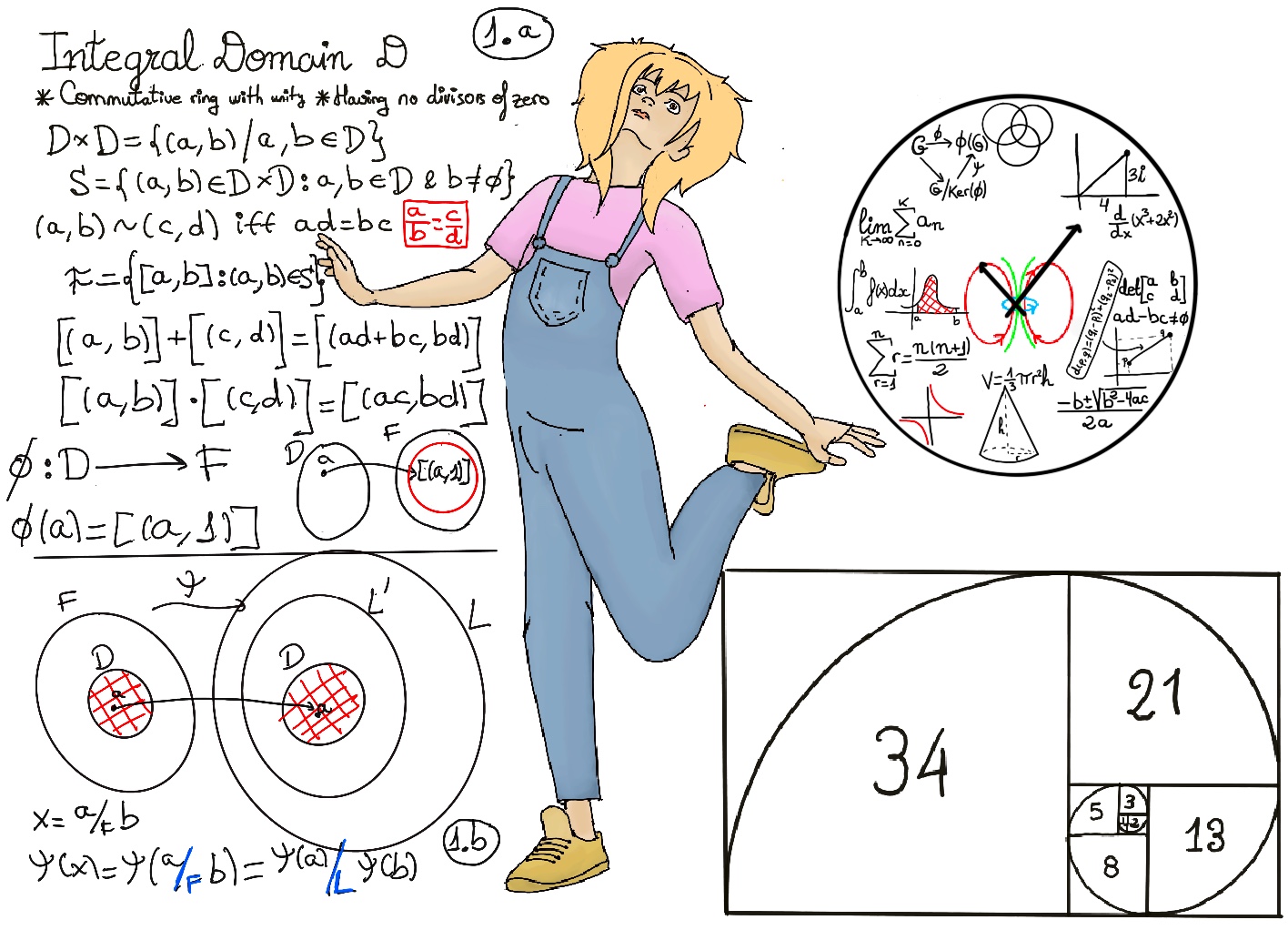
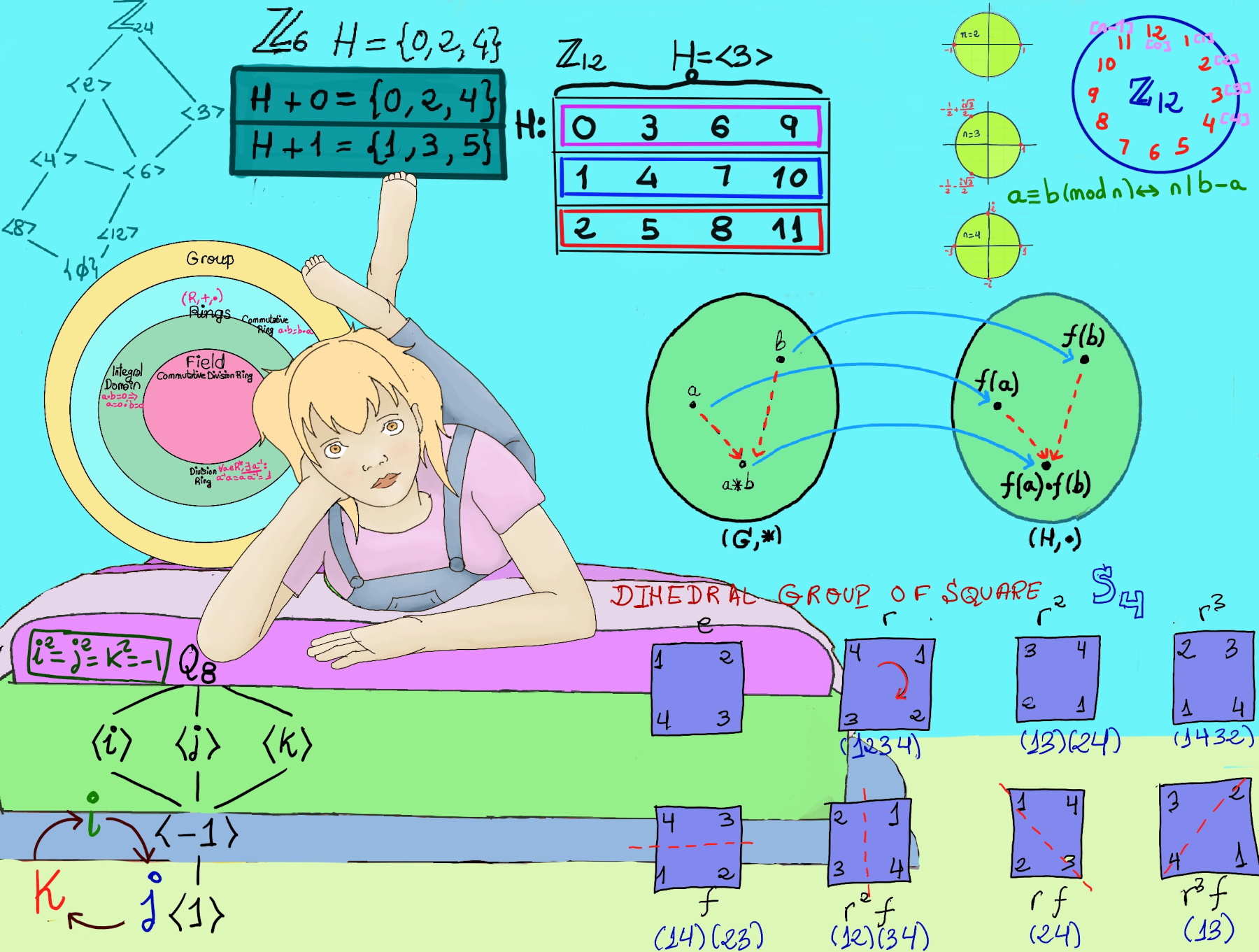
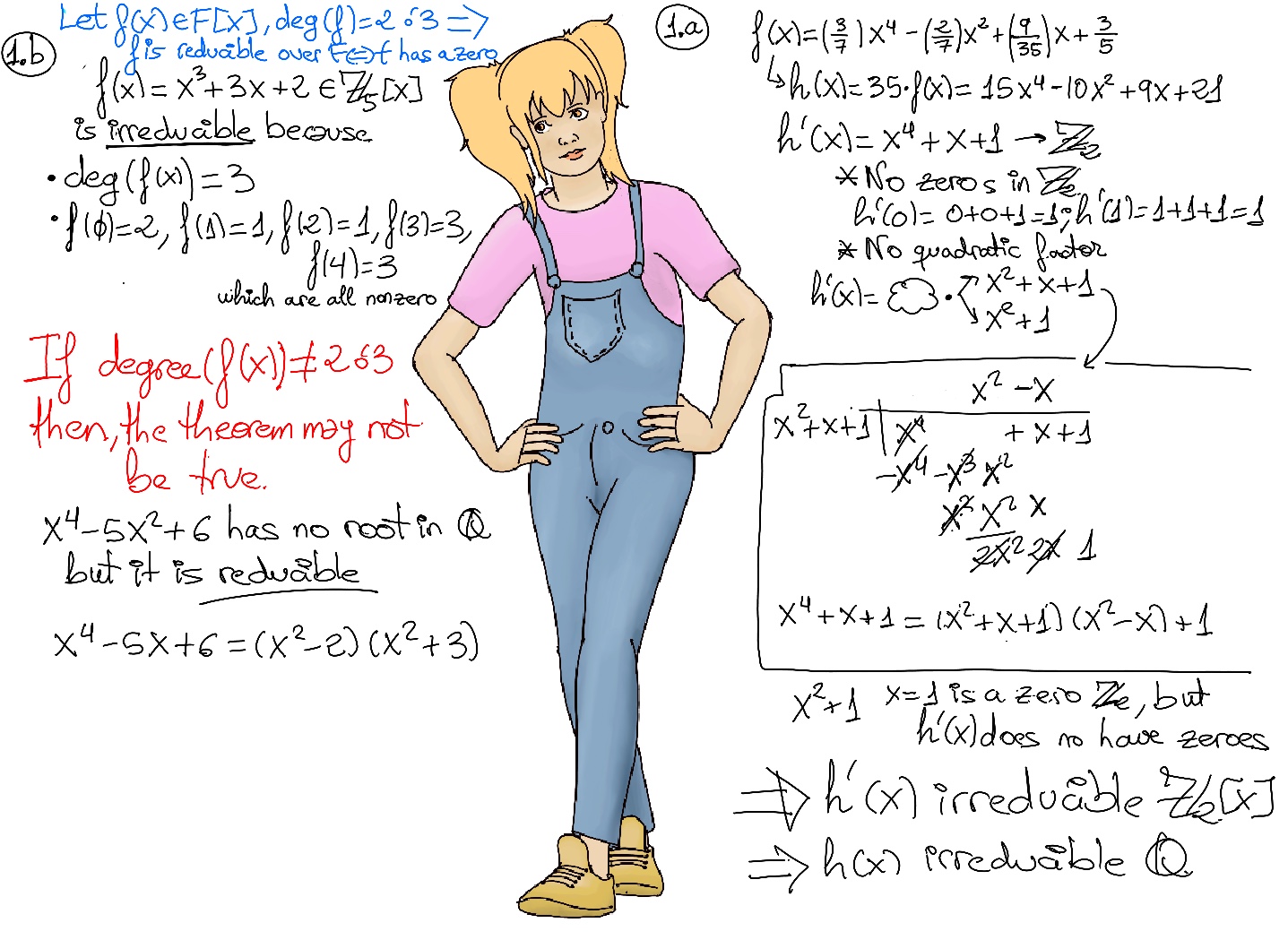
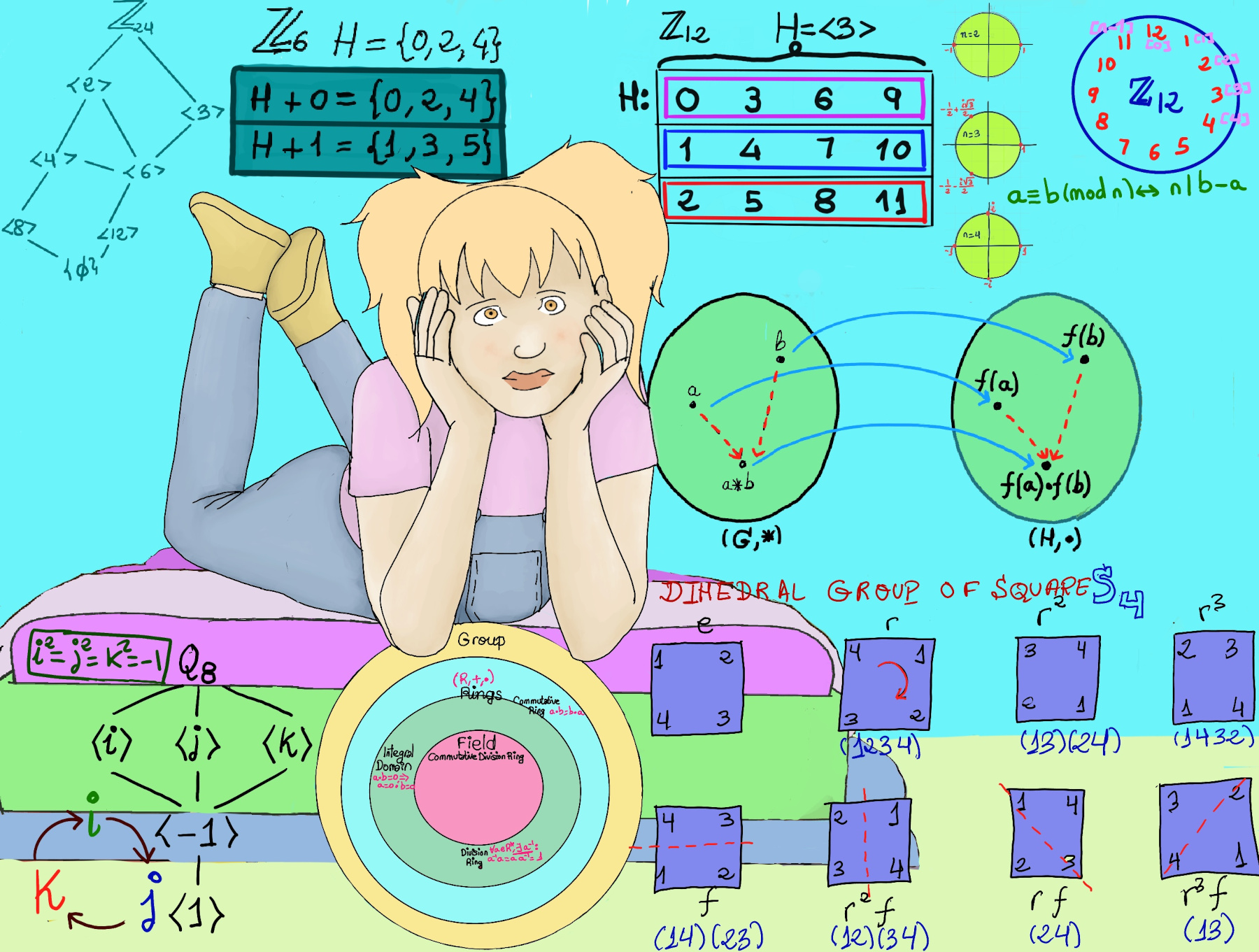
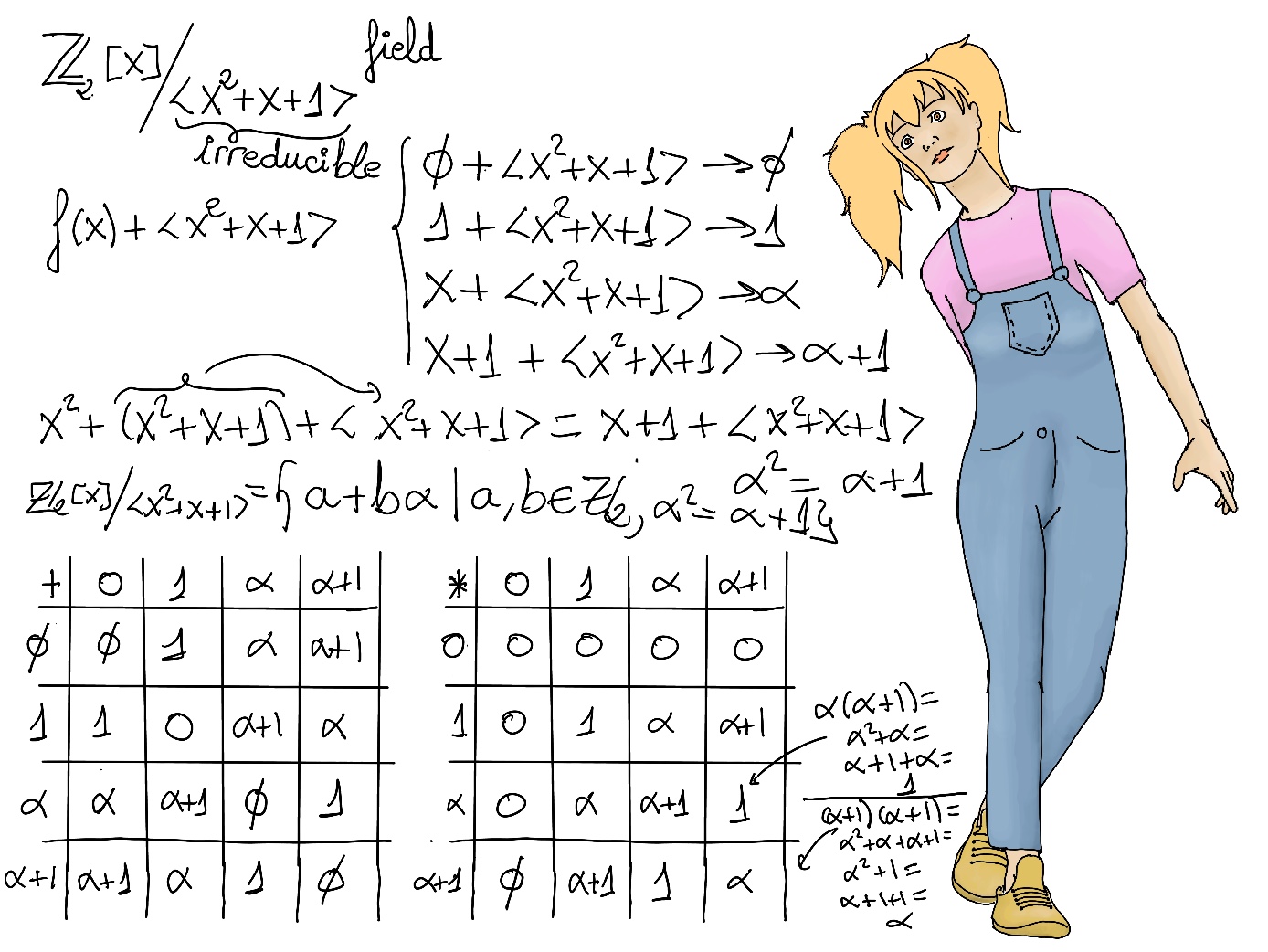
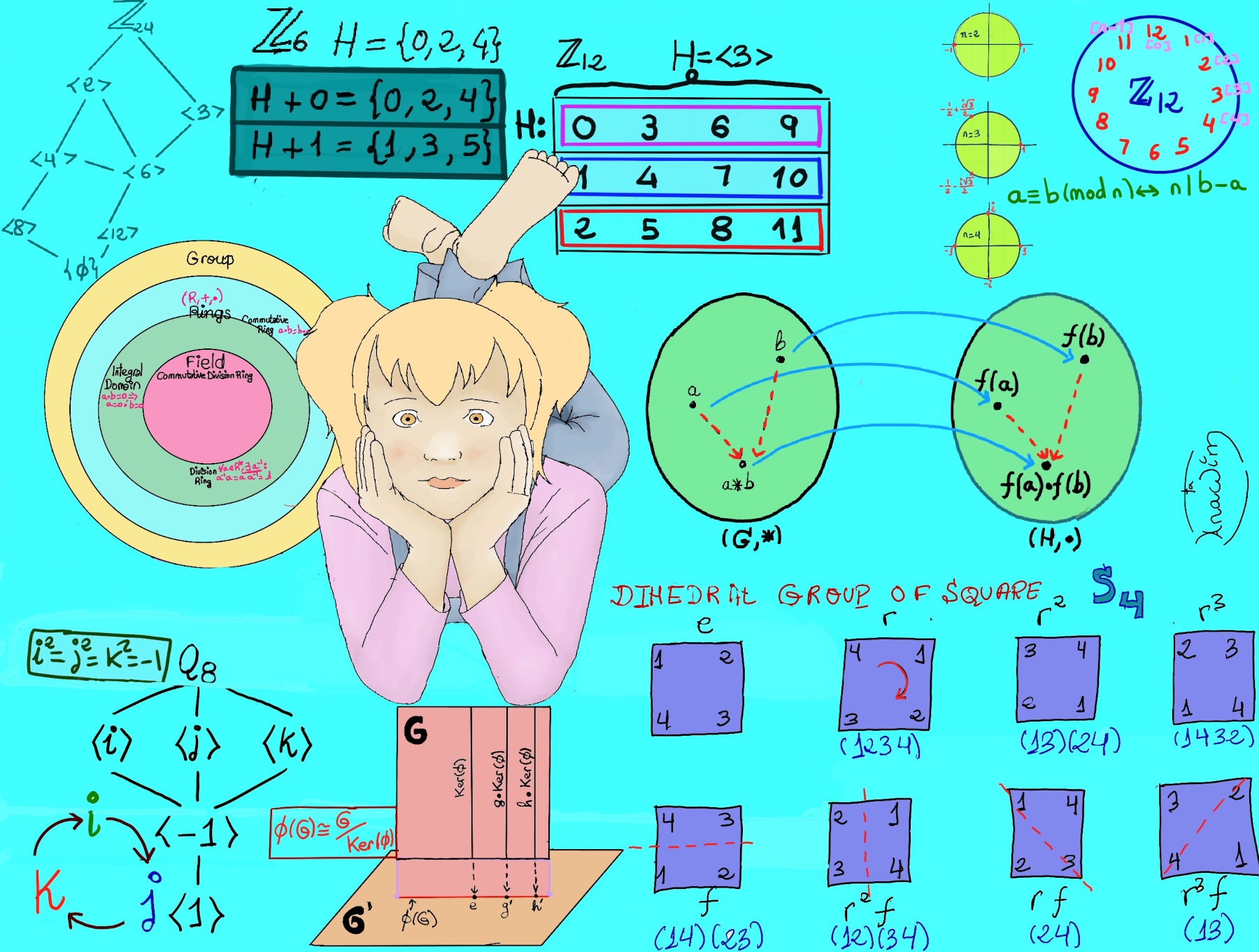
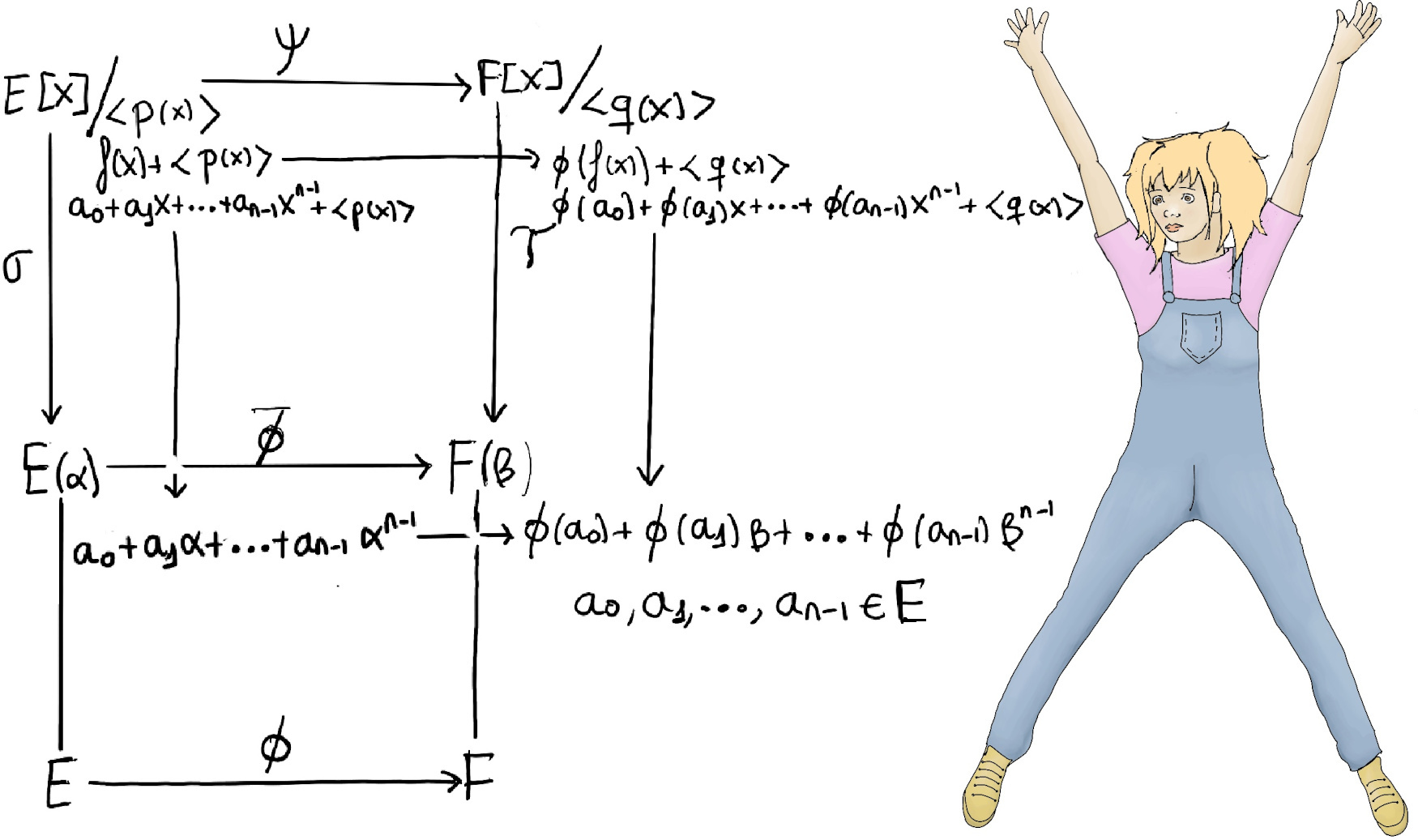
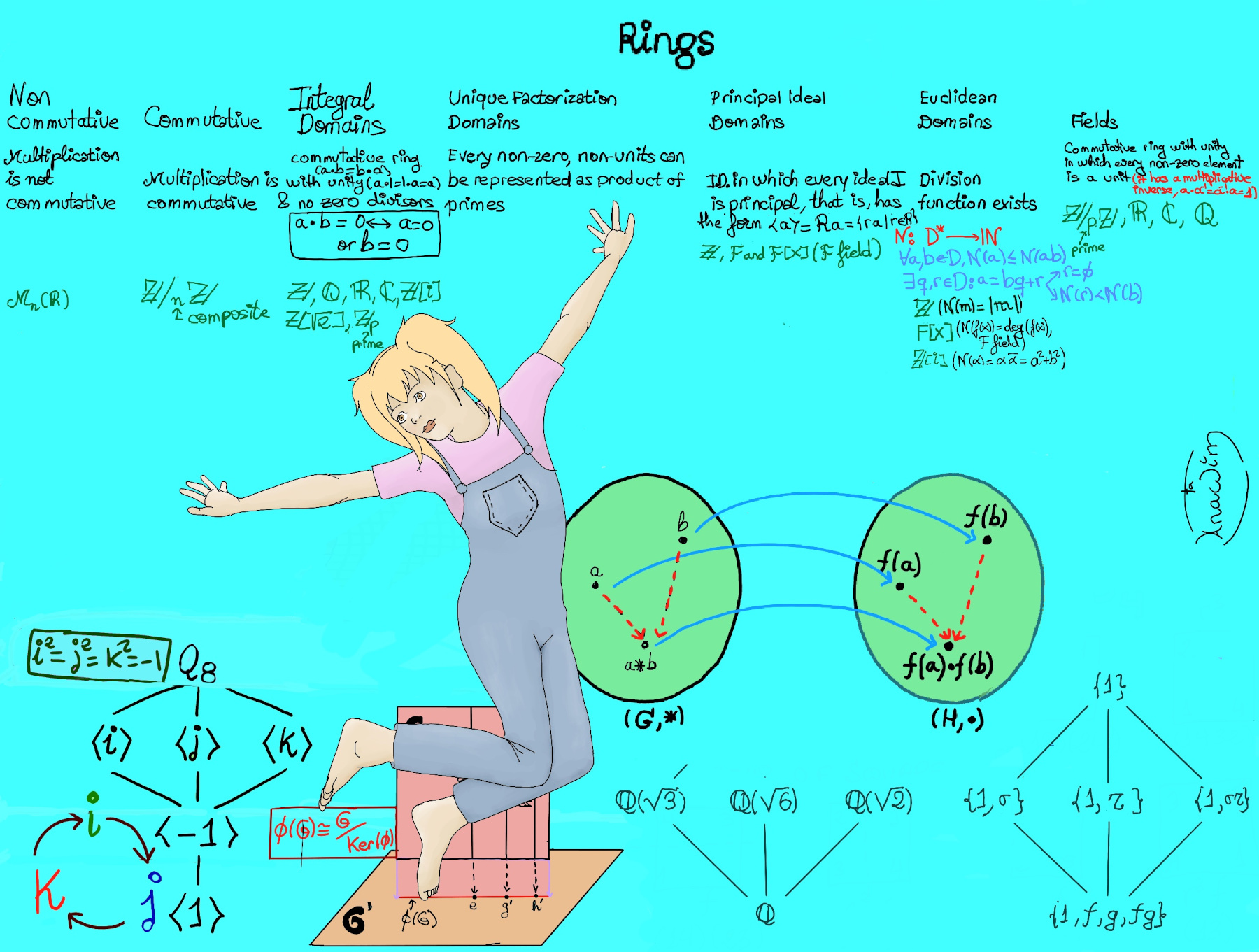
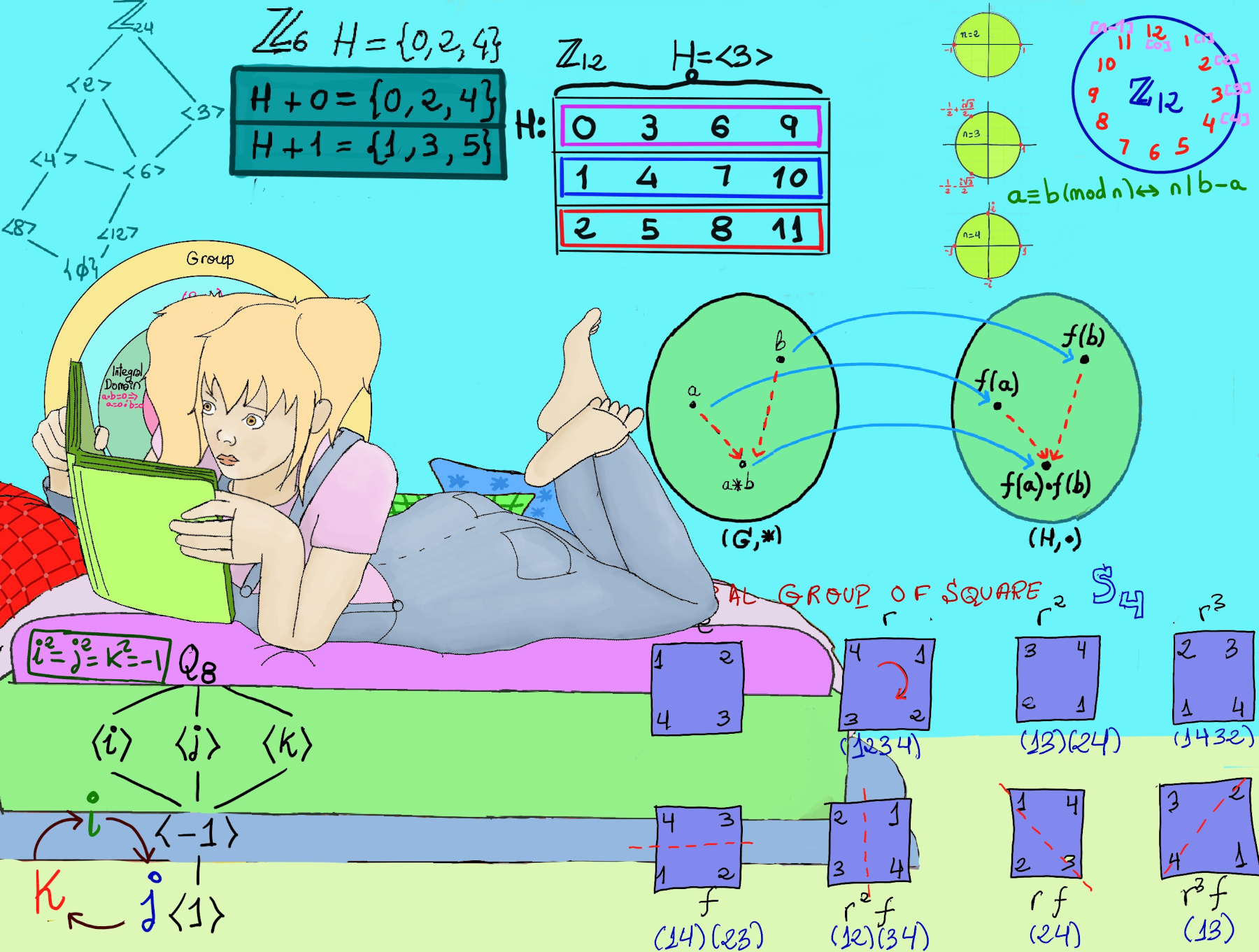
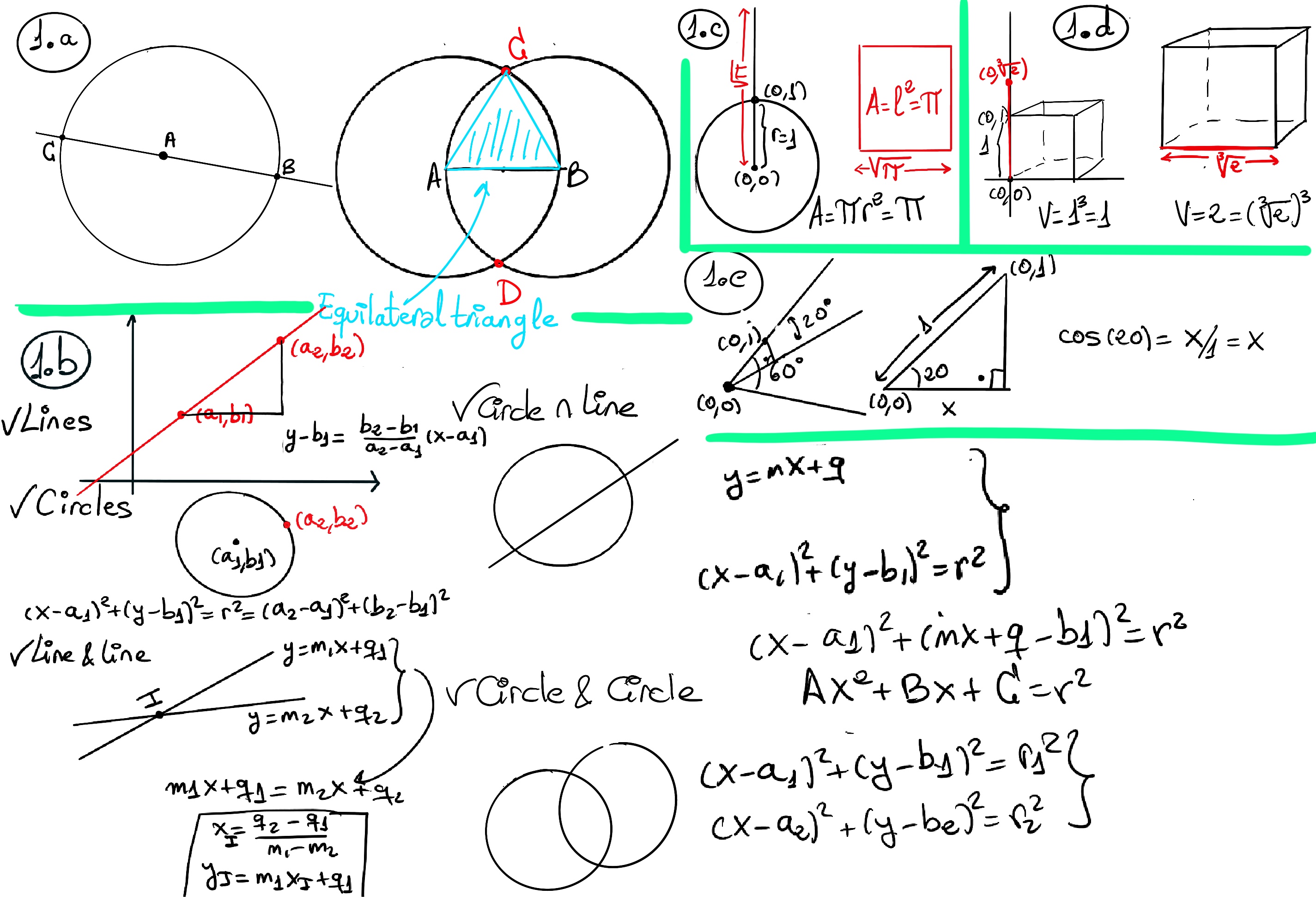
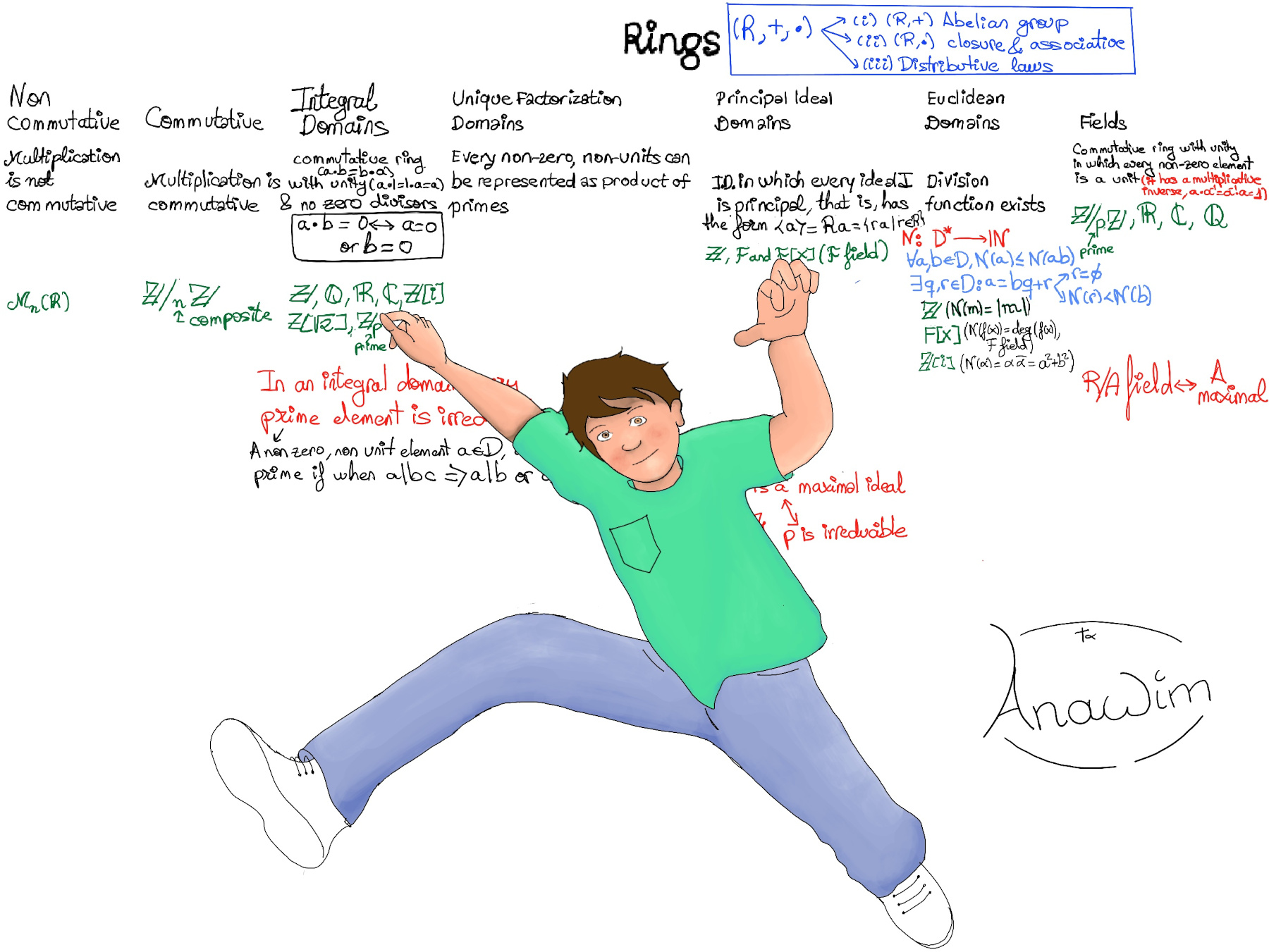
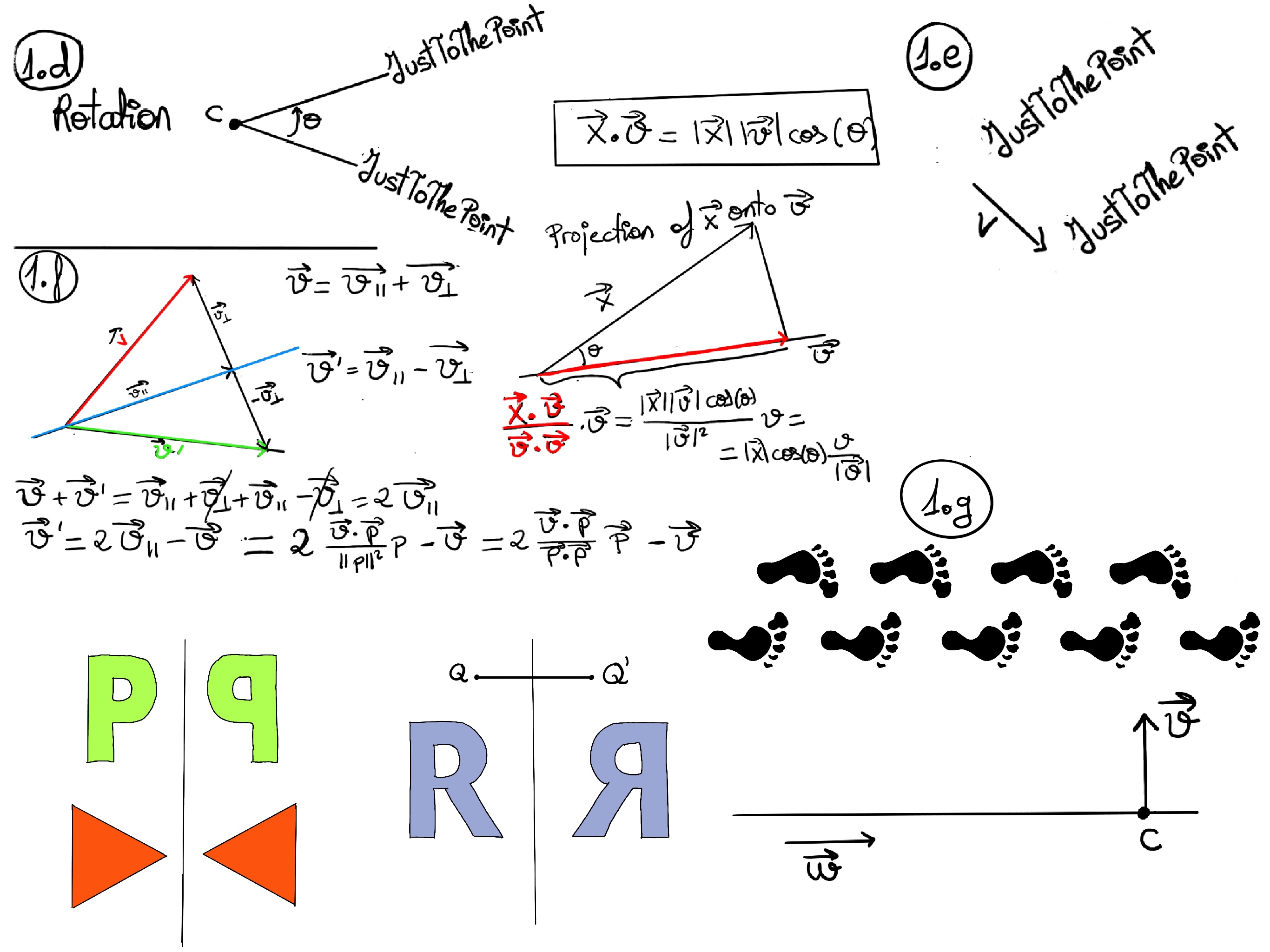
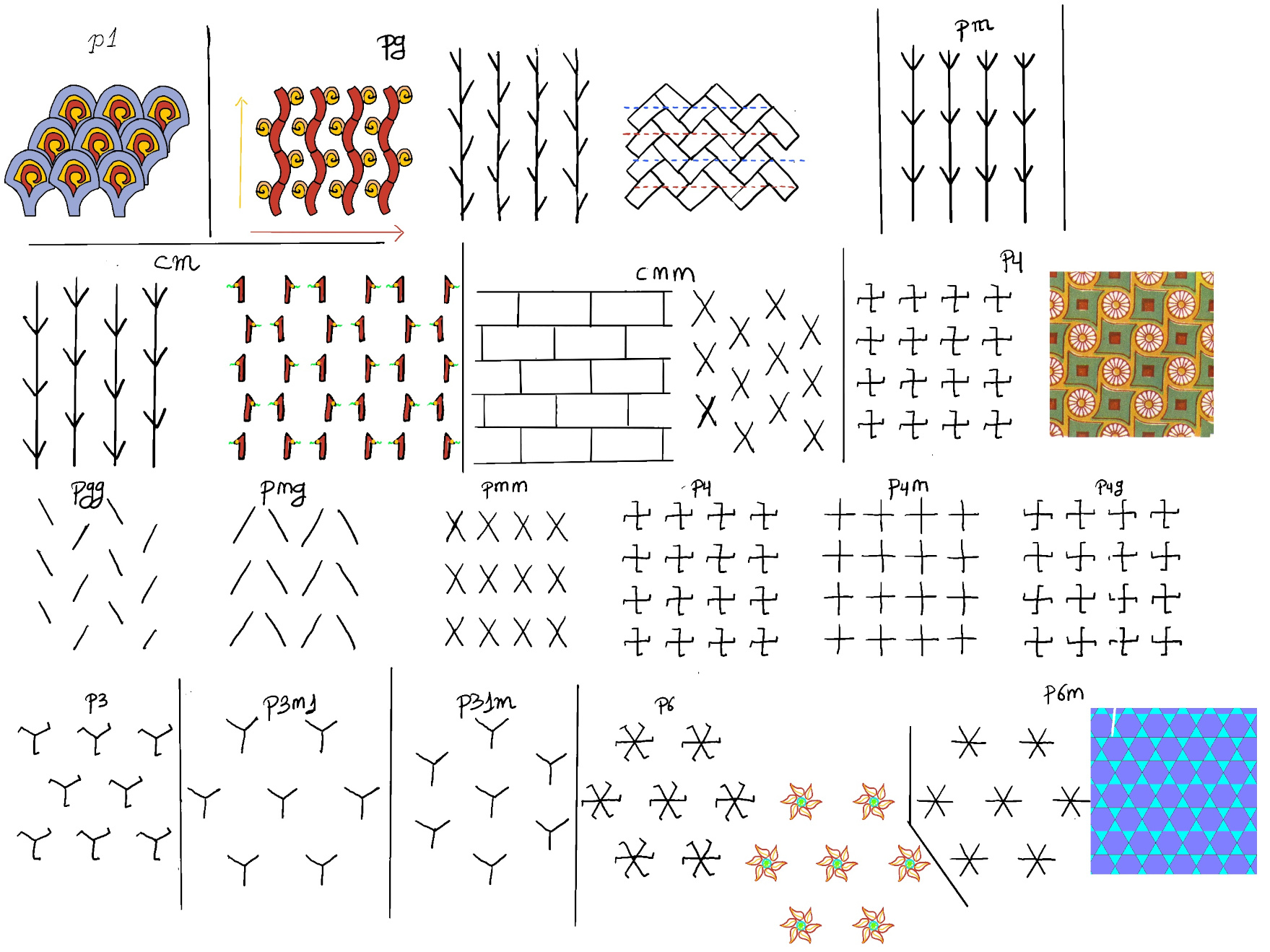
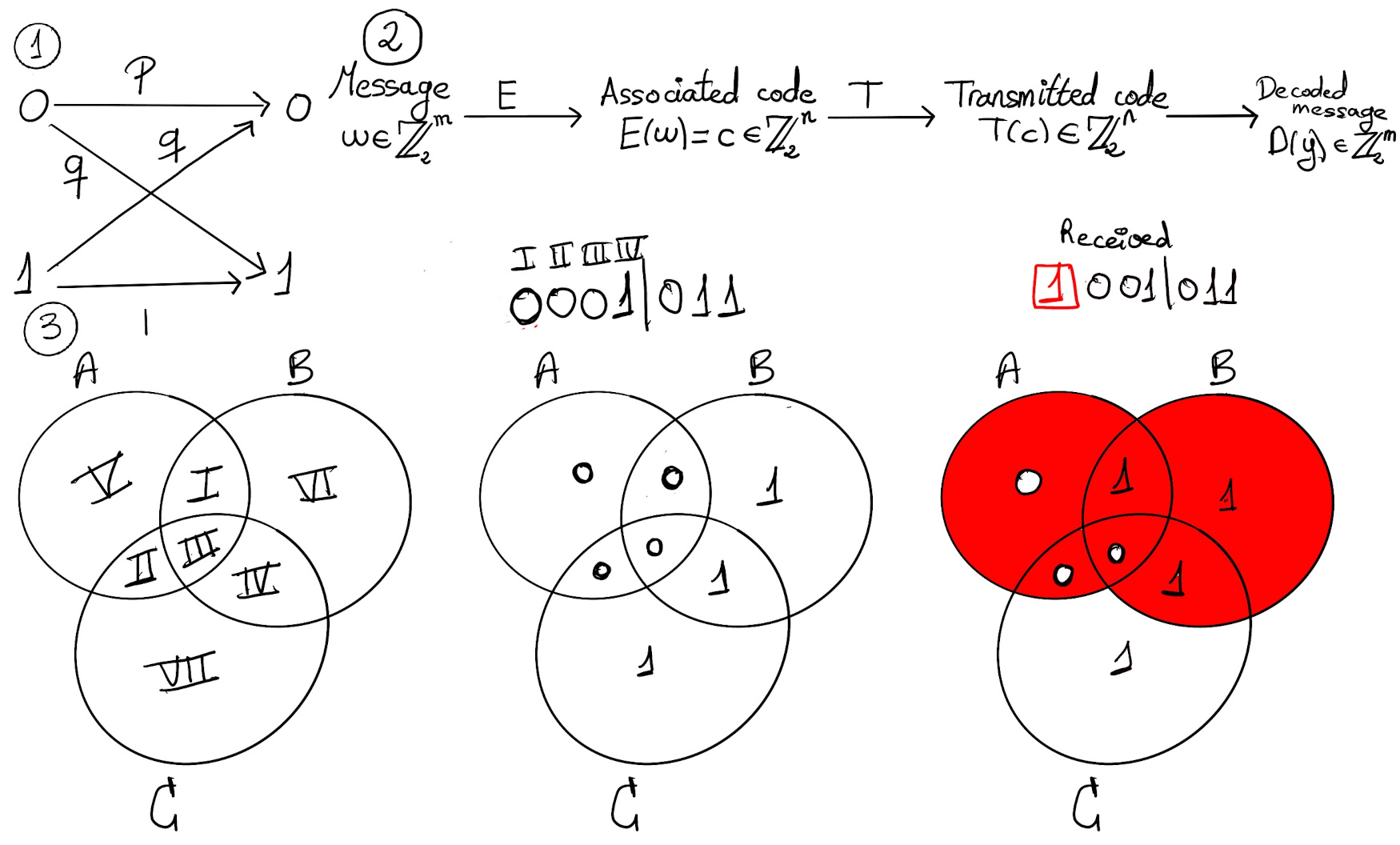
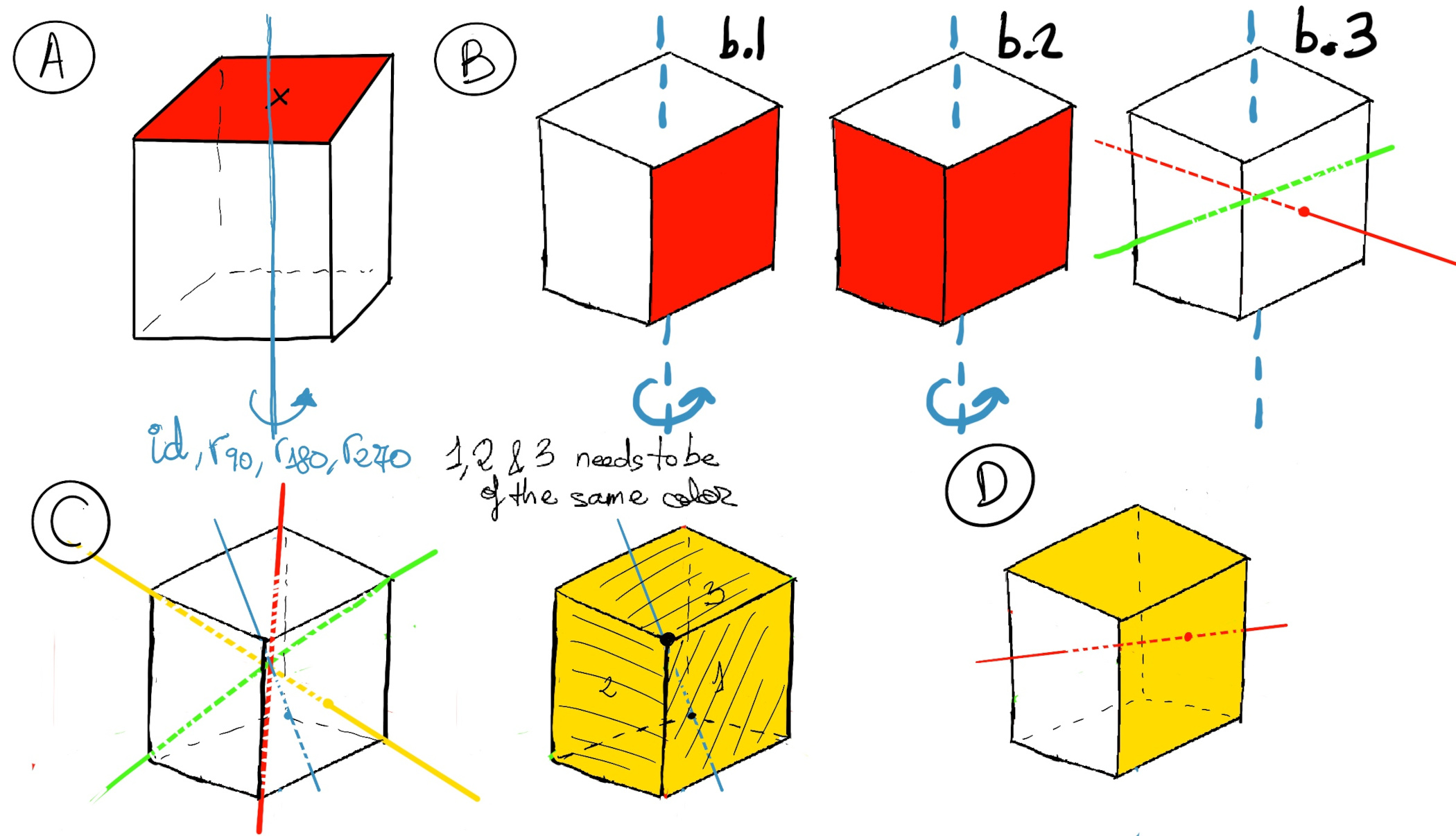
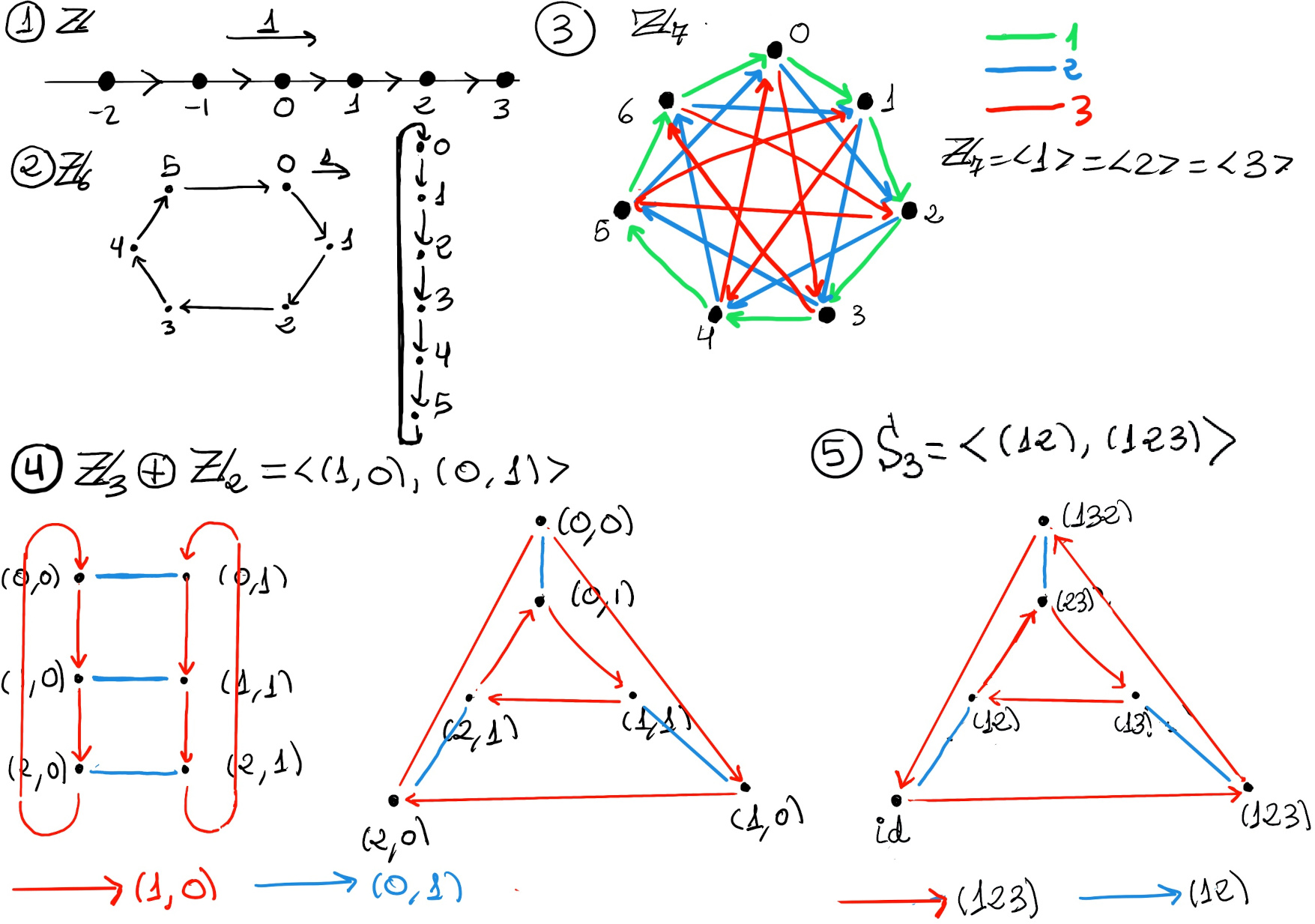
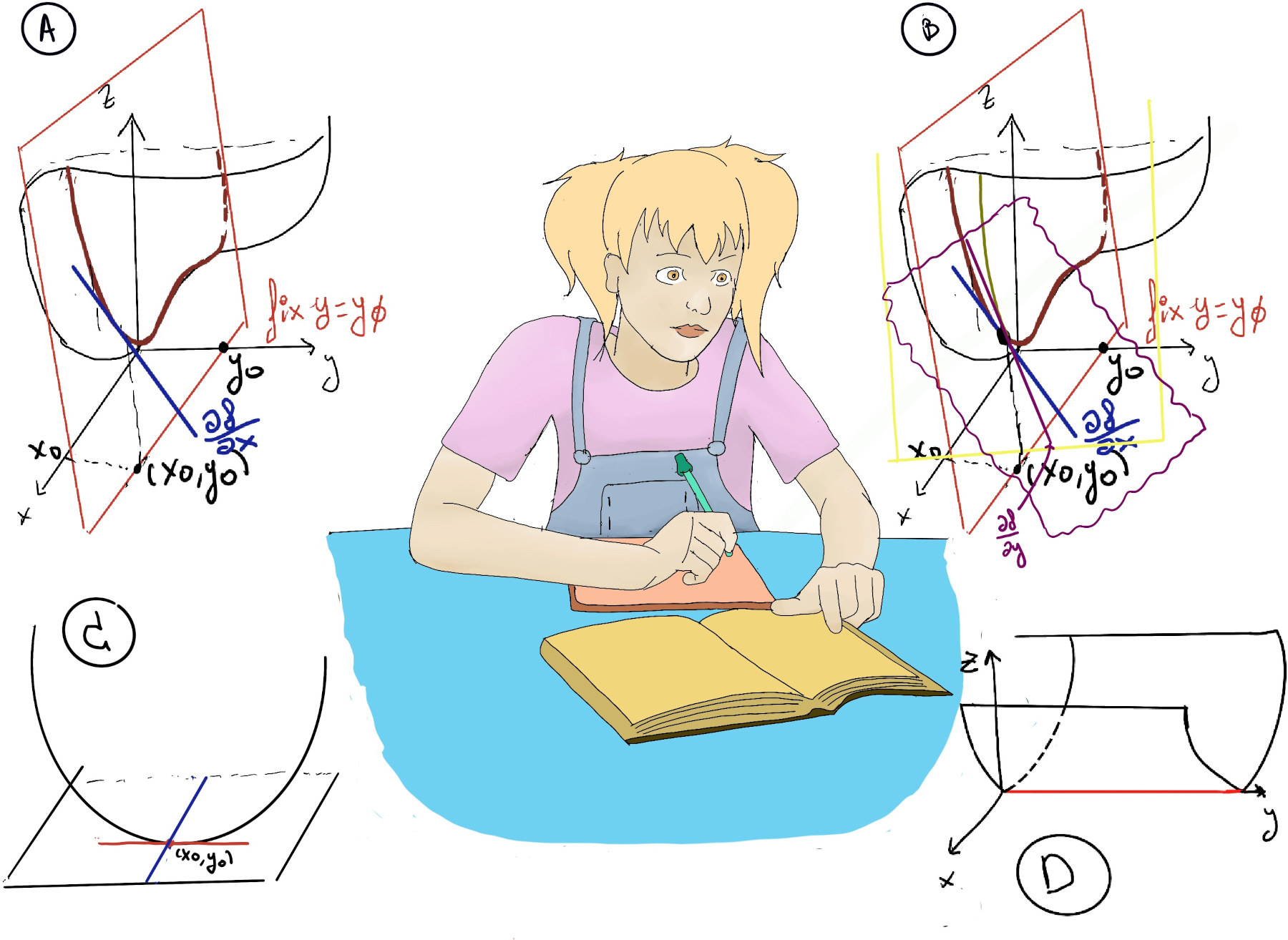
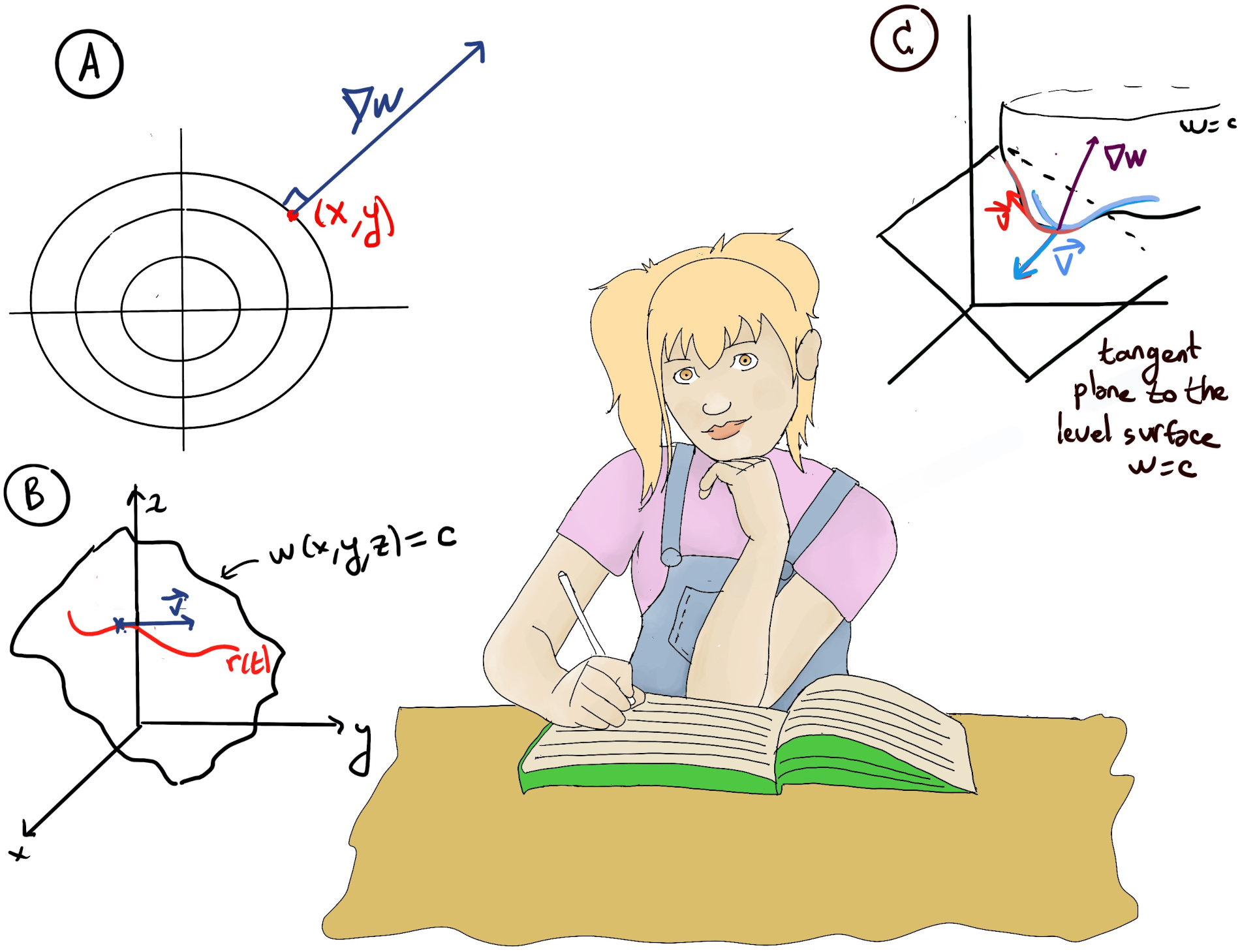
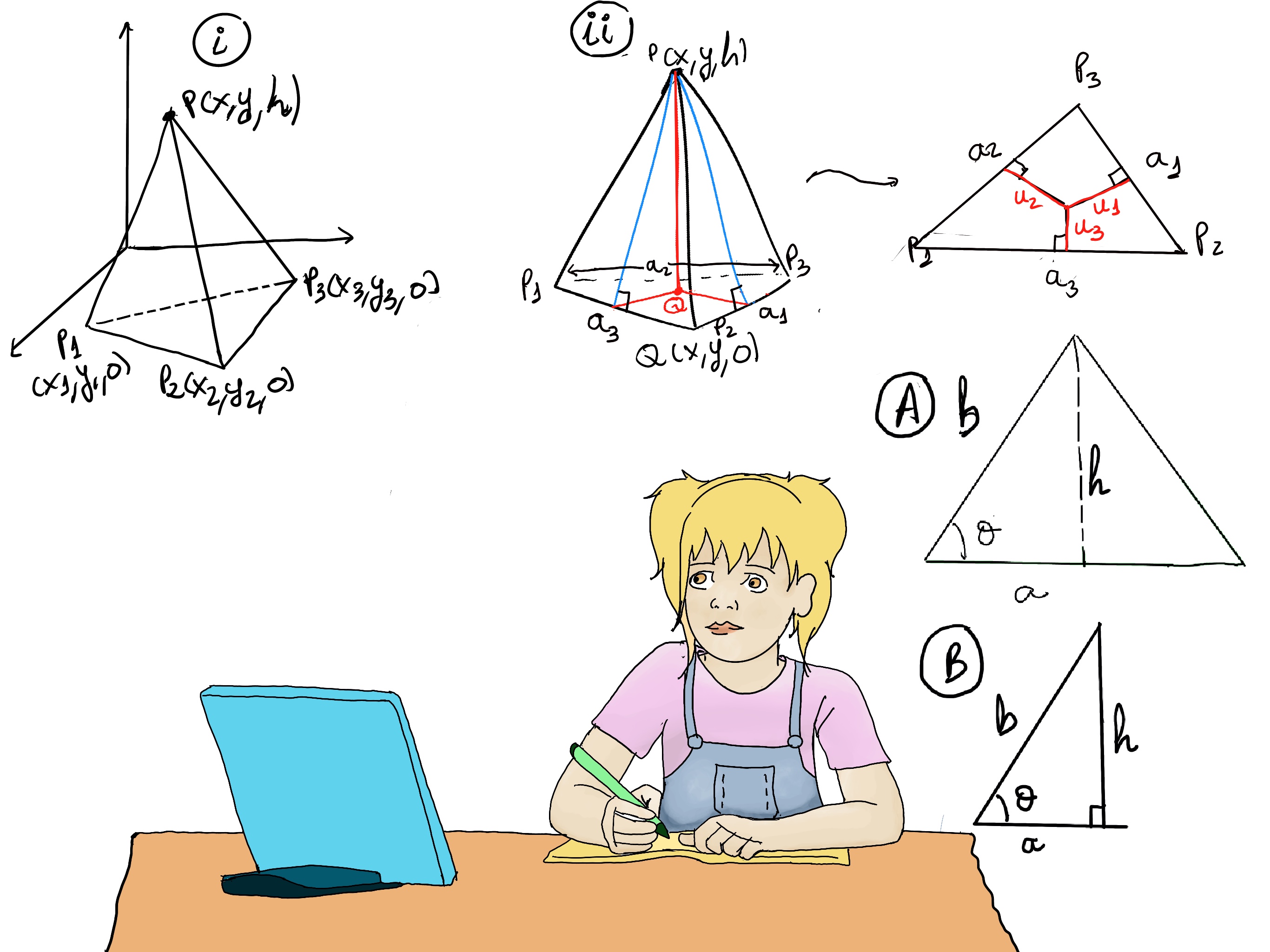
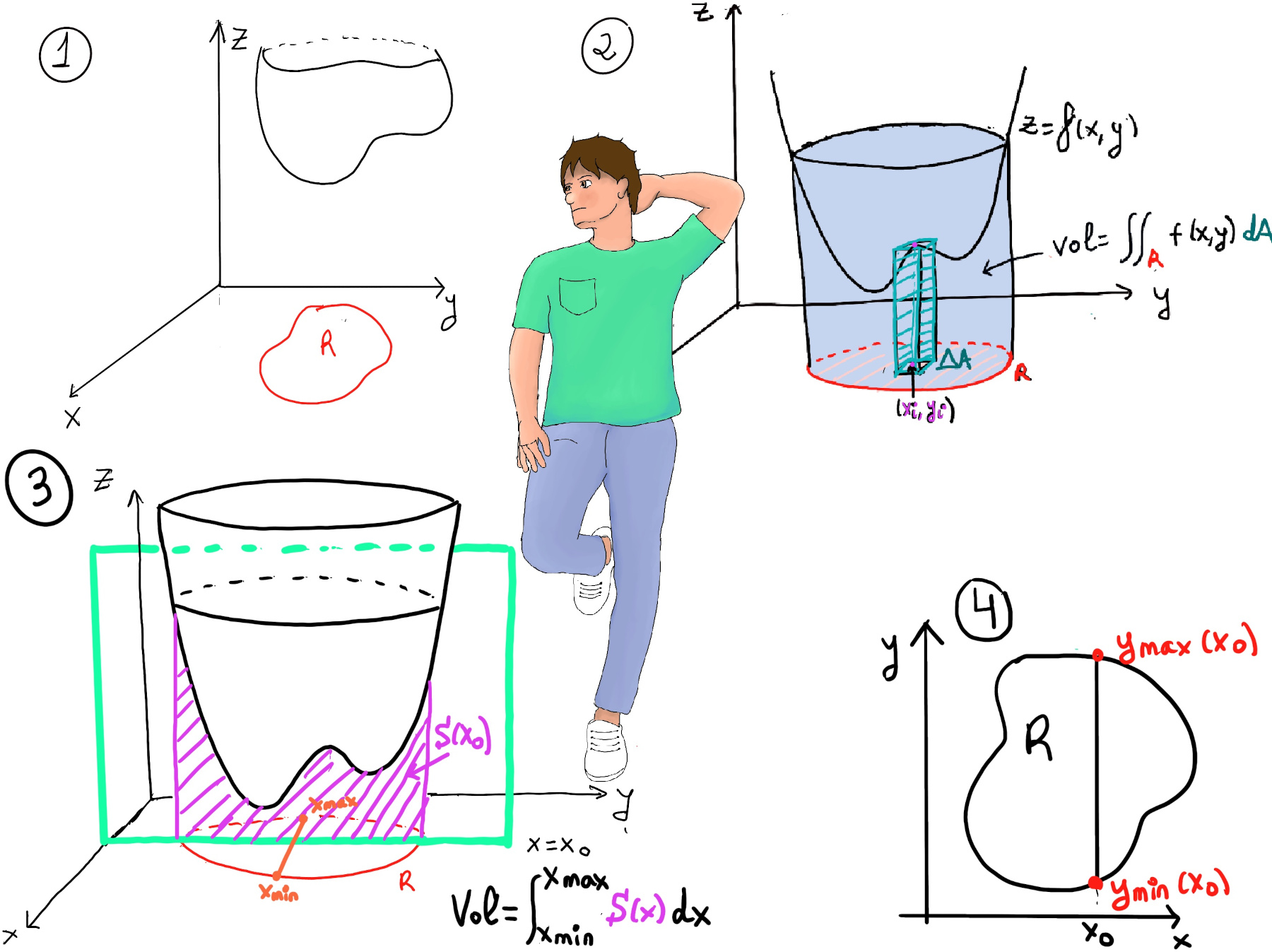
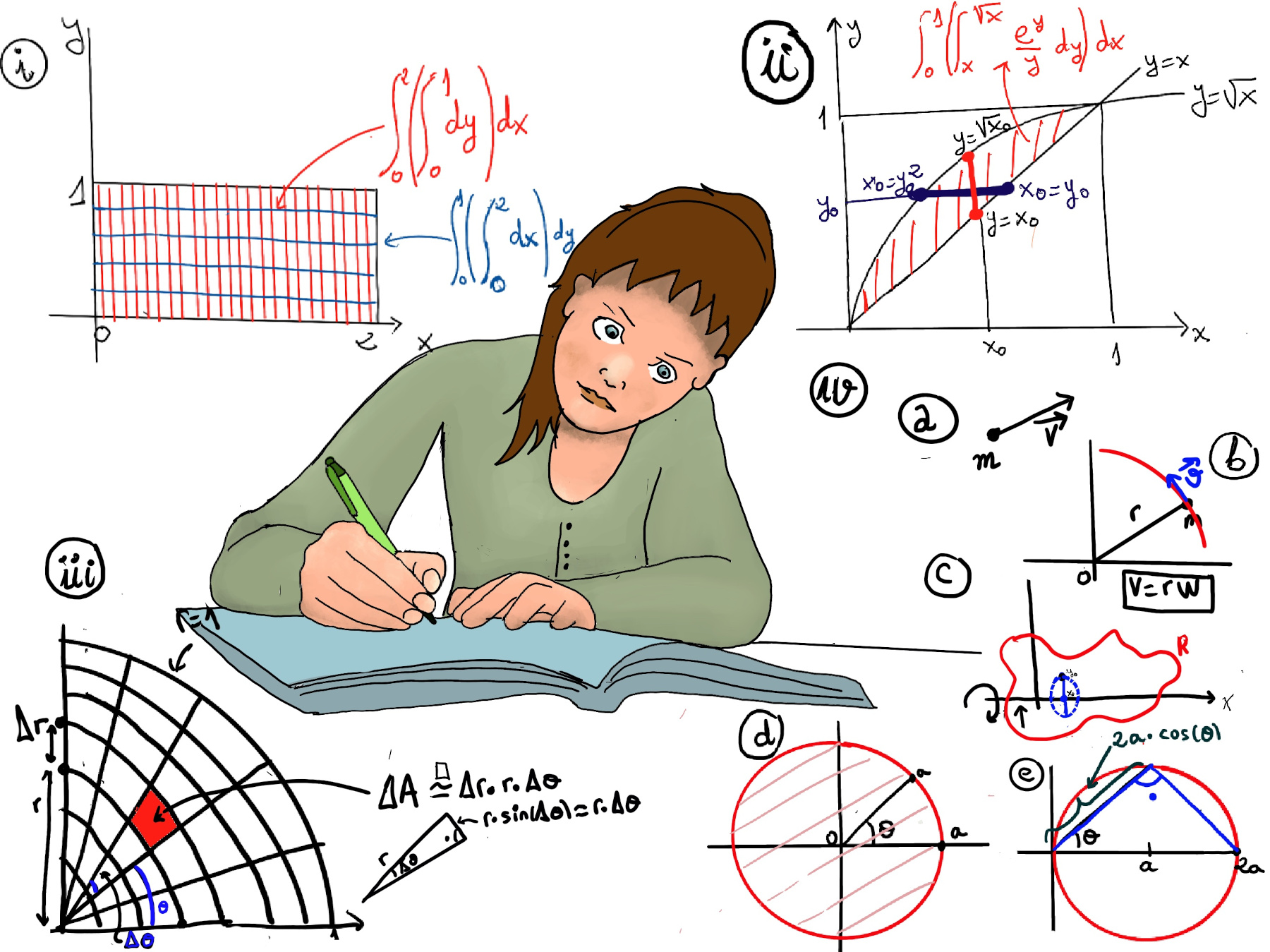
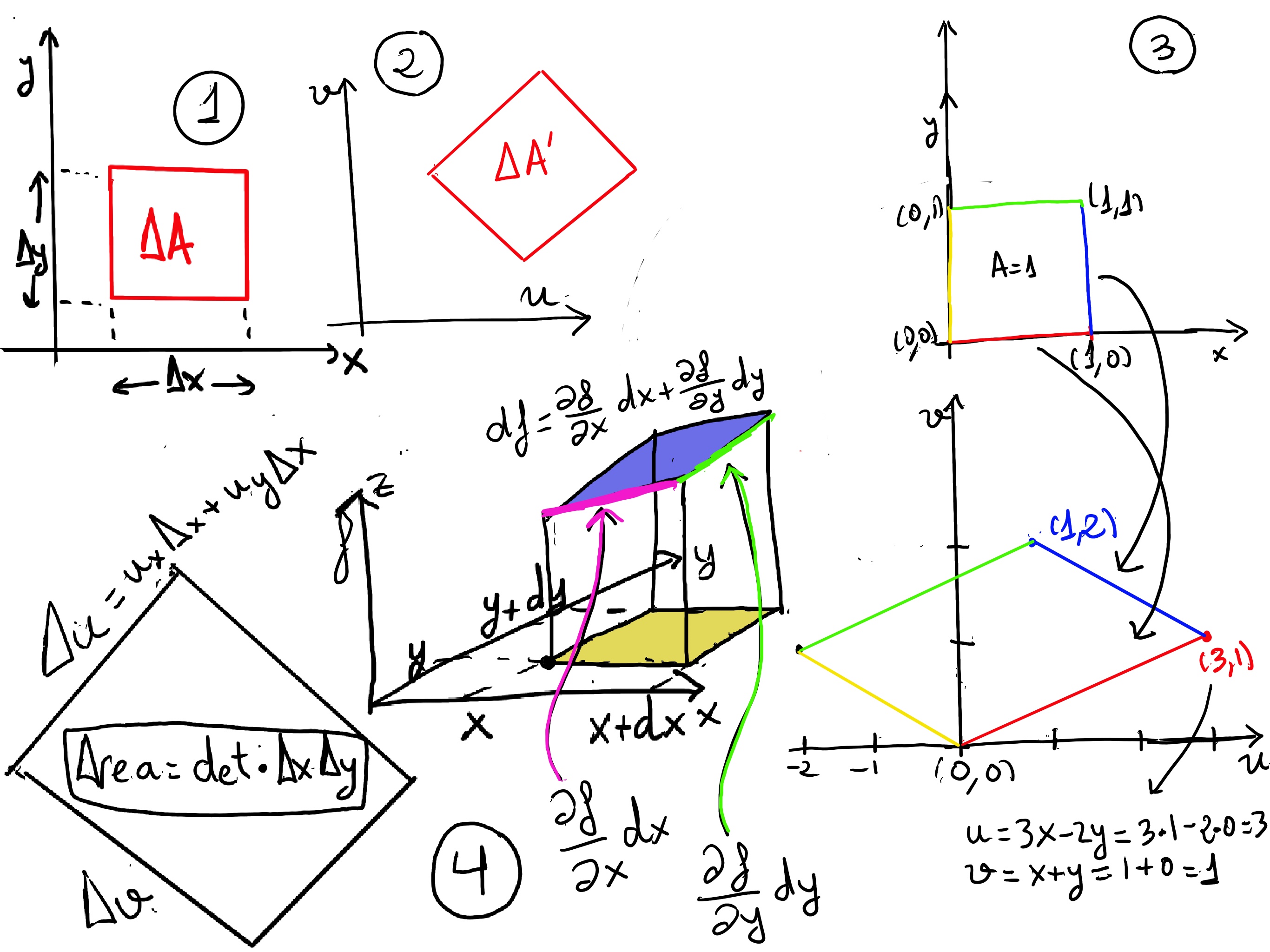
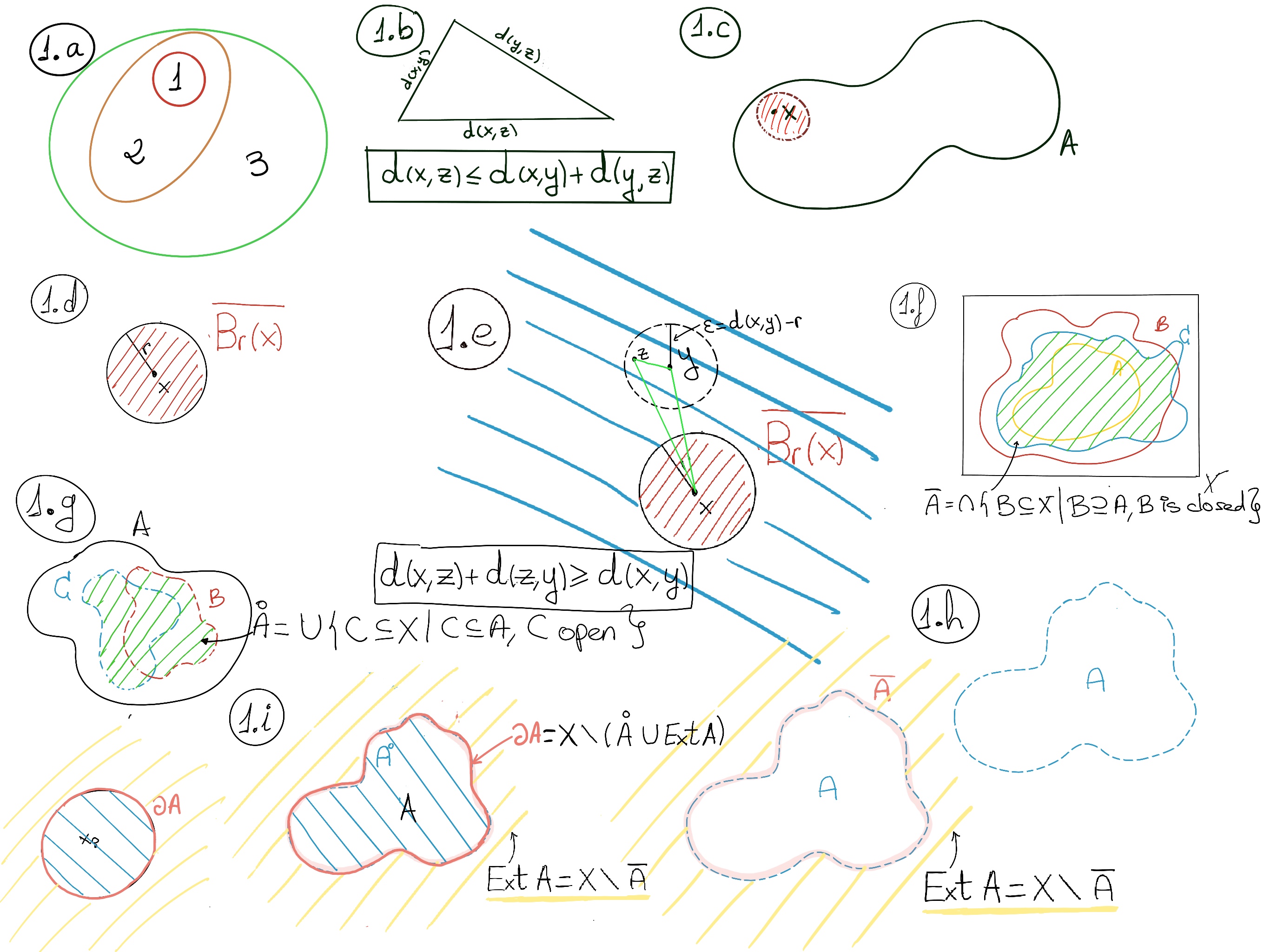
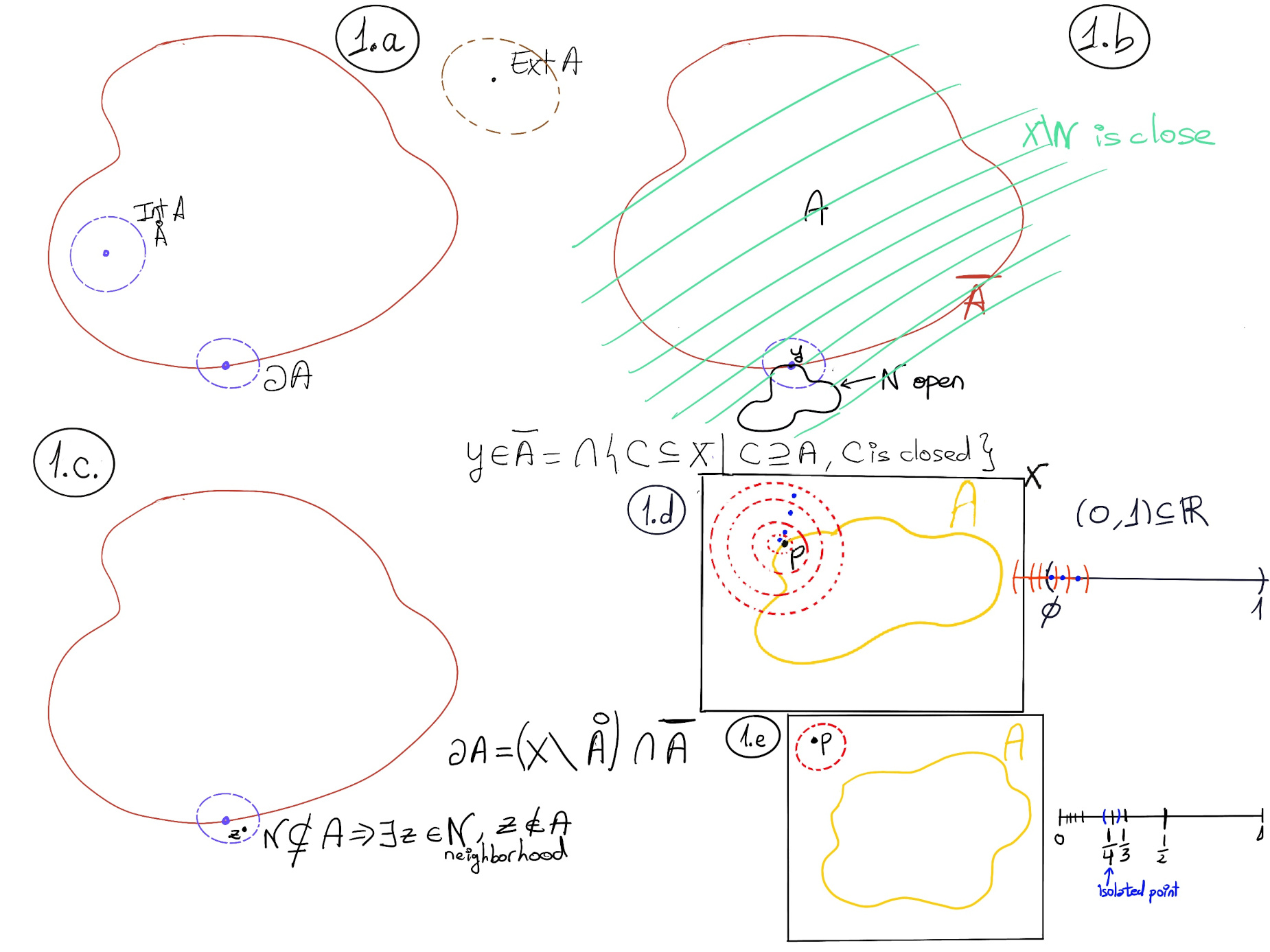
JustToThePoint Copyright © 2011 - 2024 Anawim. ALL RIGHTS RESERVED. Bilingual e-books, articles, and videos to help your child and your entire family succeed, develop a healthy lifestyle, and have a lot of fun. Social Issues, Join us.

This website uses cookies to improve your navigation experience.
By continuing, you are consenting to our use of cookies, in accordance with our Cookies Policy and Website Terms and Conditions of use.