System of linear equations

Definition: A system of linear equations is a set or collection of one or more linear equations involving the same variables of the following form: a₁x₁ + a₂x₂ + ··· + a_nx_n = b, where b and the coefficients a₁, a₂, ···, a_n are fixed numbers.

A solution to a linear system is an assignment of values to the variables such that all the equations are simultaneously satisfied. The solution set is the set of all solutions to a system of equations.

Two linear systems using the same set of variables are equivalent if each of the equations in the second system can be derived algebraically from the equations in the first system, and vice versa, and as a consequence they share the same solution set.  

Examples

• Trivial example. The system of one equation in one unknown, 6x = 18 has the solution x = 2.

A system of equations is said to be consistent or have a consistent solution if it has at least one solution, that is, there exists a set of values for the variables that satisfy all the equations in the system simultaneously. Otherwise, we call the system inconsistent.

A consistent linear system can have infinitely many solutions or a unique solution.

• The second simplest example involves two equations and two variables or unknowns, (Figure 1.a.)

$\begin{cases} 2x + 3y = 8\\\\ x + 4y = 9\end{cases}$

A linear equation of two real variables geometrically forms a line in the plane. The solution to this lineal system is the intersection between the two lines, (1, 2). This system is consistent.  

• This system of equations is inconsistent, that is, there is no solution because we can see that the two lines are parallel (Figure 1.b.)

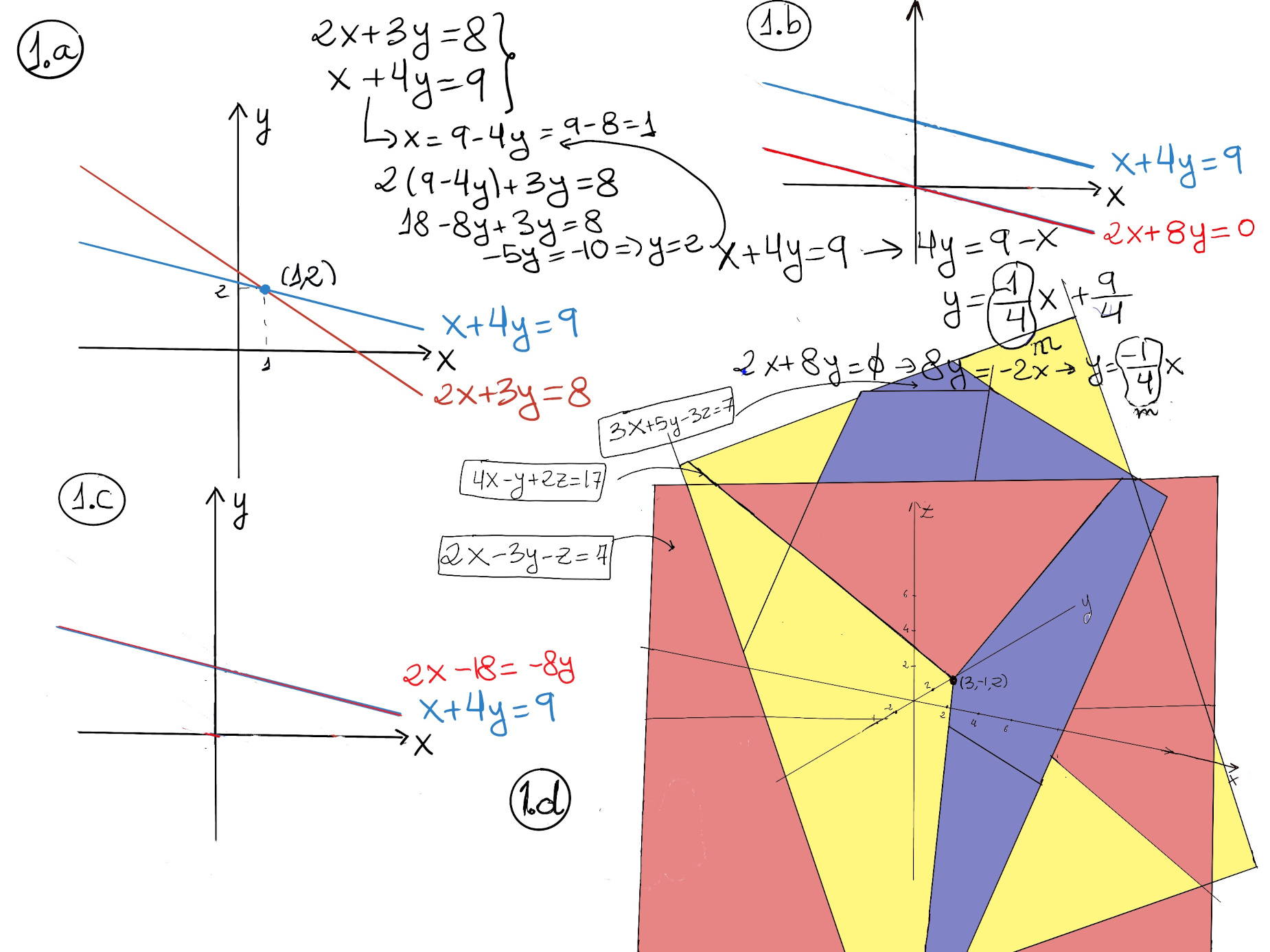
  Parallel lines have the same slope (m = ^-1⁄₄) and will never intersect.

$\begin{cases} x + 4y = 9\\\\ 2x + 8y = 0\end{cases}$

• This system of equation is consistent, but any solution that works for one equation will also work for the other equation, so there are infinite solutions to the system. (Figure 1.c.)

$\begin{cases} x + 4y = 9\\\\ 2x + -18 = -8y\end{cases}$

They two lines overlap or intersect everywhere on the line, the system is essentially expressing a single equation in multiple forms. One of the equations in the system is redundant and can be derived from the other equations, x + 4y = 9 (*2) ⇒ 2x + 8y = 18.

$\begin{cases} x + 4y = 9\\\\ 2x + 8y = 18\end{cases}$

System of two linear equations in two variables can be visually represented by graphing both equations simultaneously and the solutions to these systems of equations fall into three categories depending upon how the two lines representing each equation in the graph intersect:

1. If the lines intersect into a single point (they have different slopes), the system of two linear equations has a unique solution which corresponds to that very point (1, 2), Figure 1.a. This systems are consistent systems of independent equations.
2. A system composed of two distinct parallel lines has no solutions, and therefore it is inconsistent because these distinct parallel lines do not intersect, Figure 1.b.
3. A system can be composed of two identical lines has an infinite number of solutions because these identical lines intersect at an infinite number of points, Figure 1.c. The equations are dependent with an infinite number of solutions.

• Consider the following linear system with three variables or unknowns and three equations, figure 1.d.

$\begin{cases} 2x -3y -z = 7\\\\ 3x + 5y -3z = -2\\\\ 4x -y +2z = 17\end{cases}$

There is a solution, (3, -1, 2). Just as the graph of a linear equation in two variables creates a line, the graph of a linear equation in three variables creates a plane which extends infinitely in all directions. Therefore, a system of three linear equations in three variables can be represented as a group of three planes. Any point (3, -1, 2) which simultaneously fall on all three planes corresponds to a solution of the system.

There are different options: (1) There a no two planes parallel in the system, all planes intersect at one point, the solution to the system (Figure 2.a); (2) Two of the planes are not parallel, so they intersect in a line, and the third plane intersect the other two planes along this line, every point on this line is a solution to the system (Figure 2.b.), that is, there are infinite solutions -if the third plane is identical to one of the other two planes, the line where all planes intersect is still the solution to the system-; (3) If all planes are identical, there are also an infinite number of solutions, i.e., every point in this plane is a solution to the system (Figure 2.c.); (4) If the system has two distinct parallel planes, then there can be no solution, (Figure 2.d). Regardless of the third plane, the system is inconsistent. (5) The planes are not parallel, but they are orientated so that their intersection lie along three distinct parallel lines, and the system has no solution (Figure 2.e.)  

• Consider the following linear system with three variables or unknowns and three equations, figure 2.f.

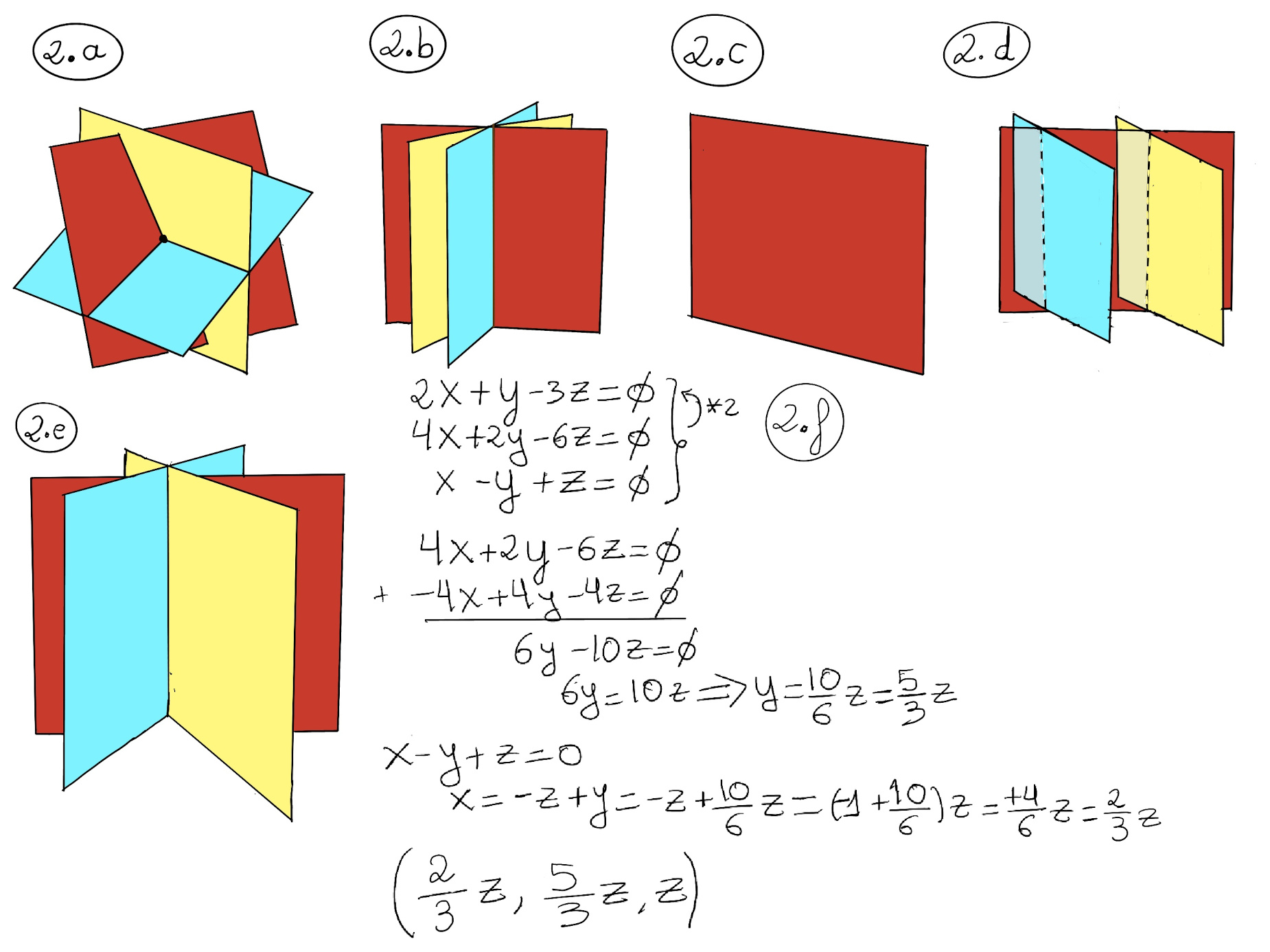
$\begin{cases} 2x + y - 3z = 0 \\\\ 4x + 2y - 6z = 0\\\\ x - y + z = 0\end{cases}$   This is the dependent (e.g., the first equation times 2 equals the second equation), consistent case. In this particular case, the three planes intersect along a common line, so any point of the form (²⁄₃z, ⁵⁄₃z, z) where the variable z can be assigned to any real arbitrary number, is a solution to the linear system. This is called the general solution to the system.

z is a free variable, that is, a variable that can be arbitrary assigned a value. On the other hand, the other two variables, x and y, are dependent variables because their values dependent upon the assignments of the free variables (in this particular case, z).

Definition. A homogeneous system of linear equations is one in which all of the constant terms are zero., that is, each equation is of the form a₁x₁ + a₂x₂ + ··· + a_nx_n = 0. Otherwise, the system is called non-homogeneous.

Example.

$\begin{cases} -x + y -z = 0 \\\\ 3x -y -z = 0\\\\ 2x + y -3z = 0\end{cases}$

This homogeneous system is consistent and has a unique solution (0, 0, 0).  

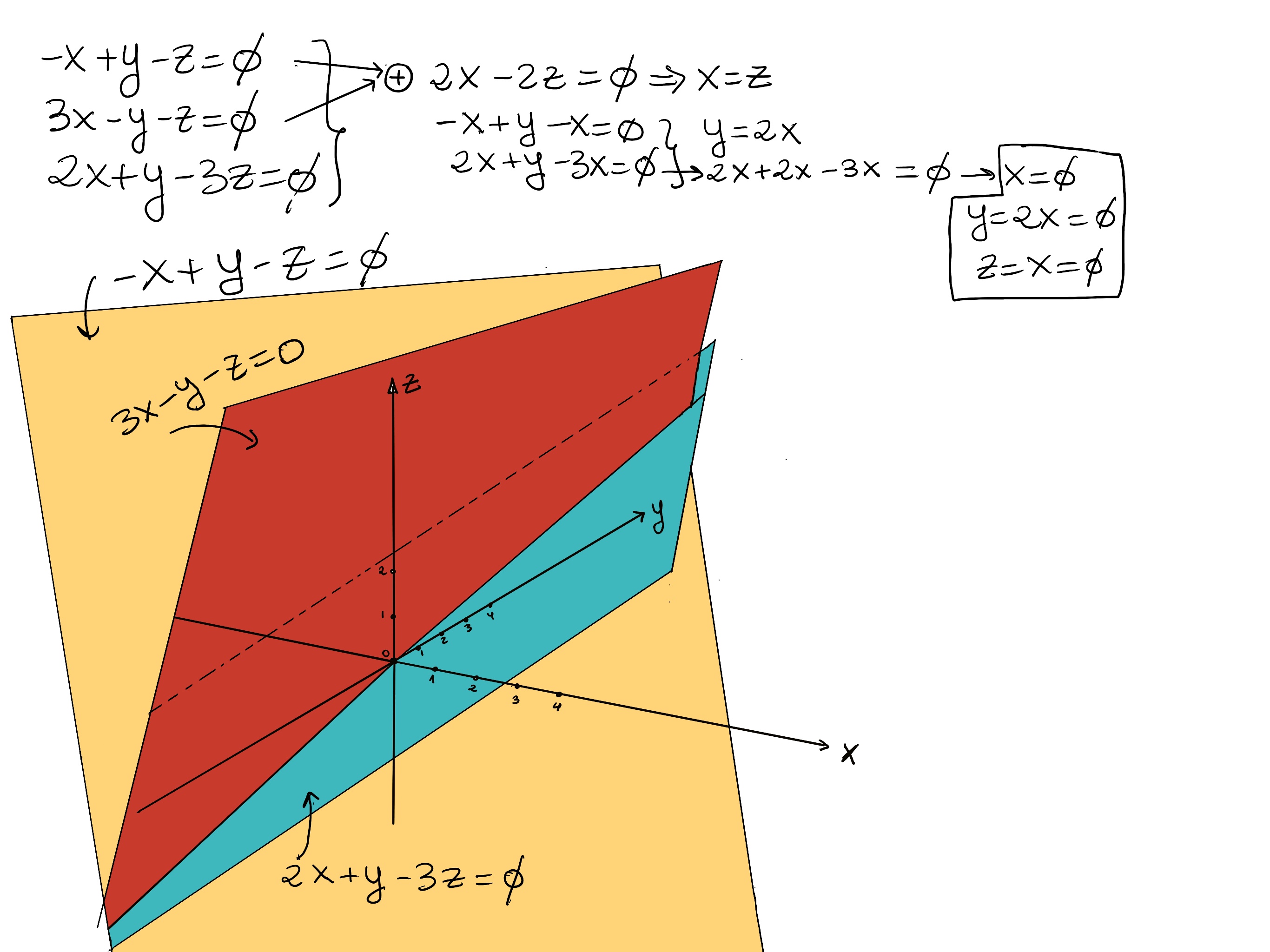
Proposition. A homogeneous system of equations is always consistent.