Convergence

Let X be a space and A ⊆ X. A point p ∈ X is a limit point of A if ever neighborhood of p contains a point of A other than p, (Fig 1.d.)  

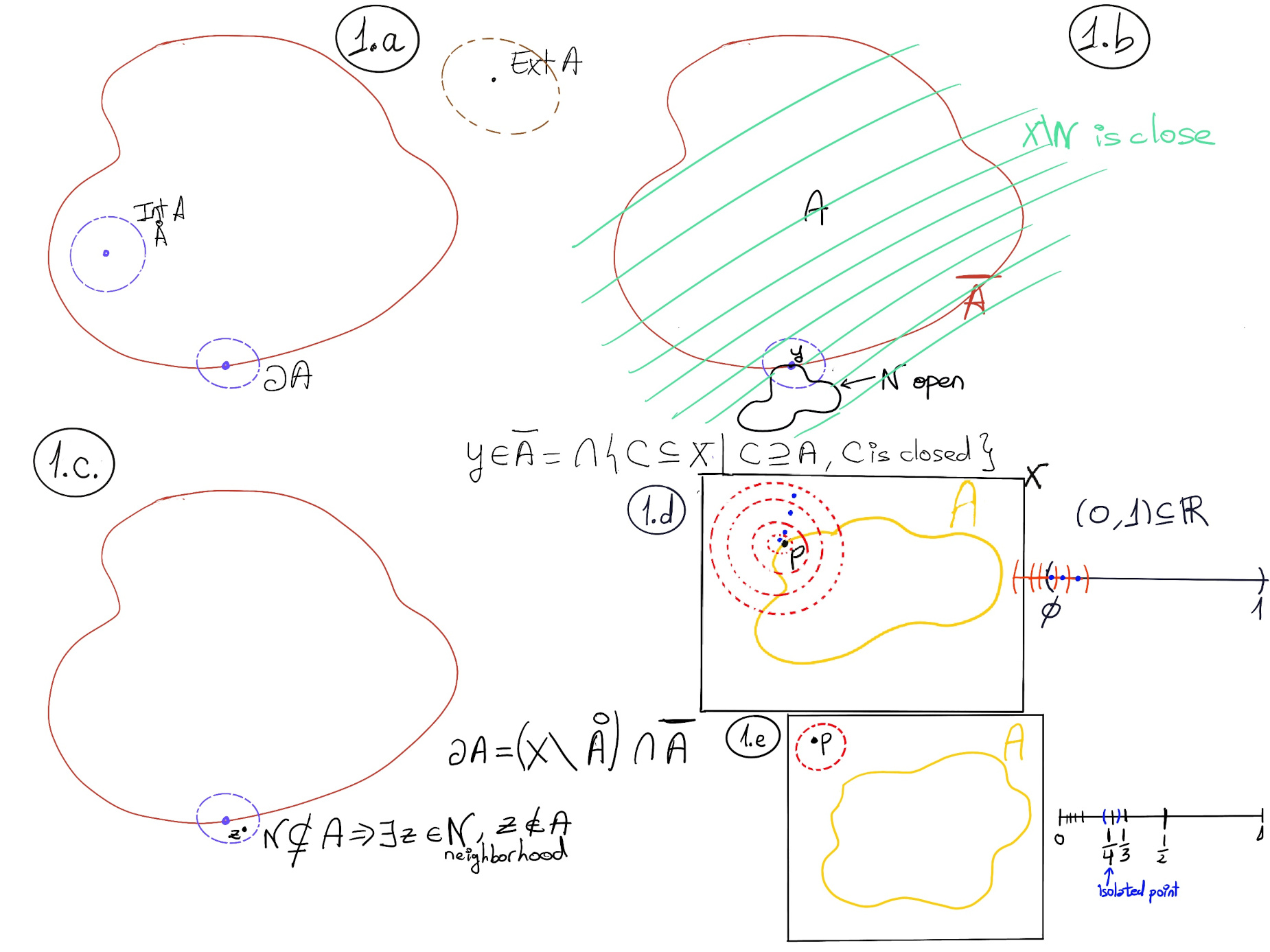
Example. (0, 1) ⊆ ℝ, their limits points are [0, 1]

Let X be a space and A ⊆ X. A point p ∈ A is an isolated point of A if p has a neighborhood U in X with U ∩ A = {p}, Figure 1.e.

Example. B = $\left.(\frac{1}{n})\right|_{n=1}^{∞}$ Every point of B is an isolated point and 0 is a limit point of B.

Definition. A subset A of a space X is dense in X if $\bar A=X,$e.g., ℚ is dense in ℝ because every real number either is a rational number or has a rational number arbitrary close to it.

Proposition. A subset B is dense in X iff every non-empty open set C, C ⊆ X contains a point of B.

Proof.

⇒ Suppose B is dense in X ⇒ $\bar B=X$. Let C be a non-empty (∅) open set, C ⊆ X. Let c ∈ C ⊆ X $=\bar B$ ⇒ Every neighborhood of c contains a point of B.

⇐ Suppose every non-empty open set C, C ⊆ X contains a point of B. We claim that $\bar B=X$. Let x ∈ X, we claim that x ∈ $\bar B=X$ ↭ every neighborhood of x contains a point of B.

x ∈ X, let U be an arbitrary neighborhood of x, therefore U is an open subset of X, U ≠ ∅ (x ∈ U) ⇒ [By assumption] it contains a point of B ⇒ x ∈ $\bar B=X$

Definition. If X is a space, $\left.(x_i)\right|_{i=1}^{∞}$ is a sequence of points in X, and x ∈ X, we say the sequence $\left.(x_i)\right|_{i=1}^{∞}$ converges to the limit x if for every neighborhood U of x there exist N ∈ ℕ such hat x_i ∈ U for all i ≥ N, (Figure 1.a)

Proposition. For A ⊆ X and $\left.(x_i)\right|_{i=1}^{∞}$ ⊆ A with x_i → x, then x ∈ $\bar A$.

Proof.

Let’s suppose that A ⊆ X and $\left.(x_i)\right|_{i=1}^{∞}$ ⊆ A with x_i → x. We claim that x ∈ $\bar A$ ↭ every neighborhood of x contains a point of A.

Let U be an arbitrary neighborhood of x ⇒ [By definition] there exist N ∈ ℕ such hat x_i ∈ U for all i ≥ N. In particular, x_N ∈ U, and U was selected arbitrary, so therefore x ∈ $\bar A$.