Extension Theorems II

I used to think that I was depressed, insane, self-absorbed, overthinking too much, left unsupervised for too long, and surrounded by assholes, dick-suckers, and jerks. Now, I am starting to realize that rock bottom has a basement and a cellar, the world is getting crazier, nastier, and more meaningless, and I have psychological problems beyond psychologists wildest nightmares and philosophers senseless mental masturbations, Apocalypse, Anawim, #justtothepoint.

Theorem. Let L/K be an algebraic extension. Every field homomorphism Φ: K → C where C is an algebraically closed field, can be extended to a homomorphism L → C

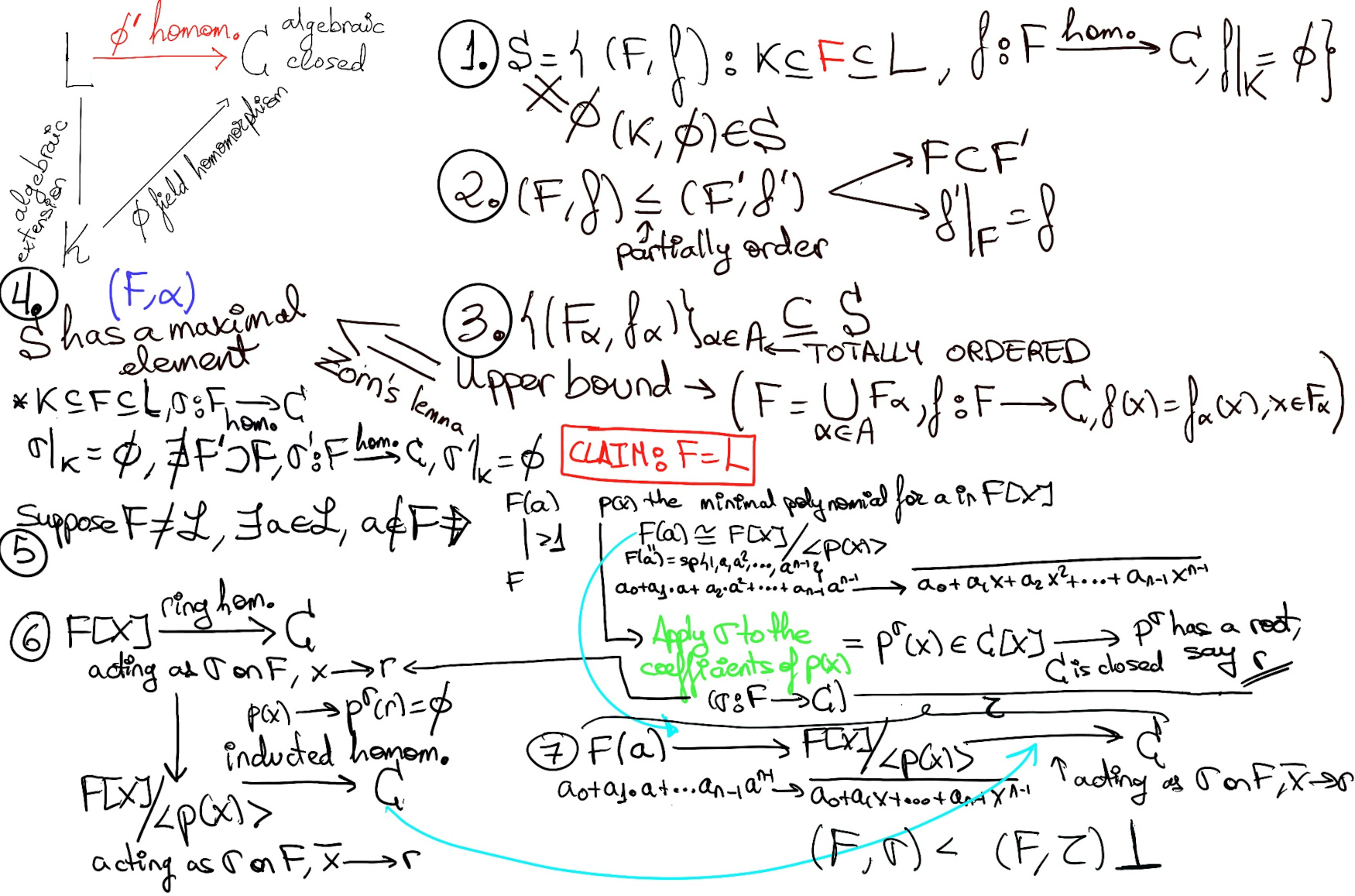
Proof.

Let S be the set of pairs (F, f) where F is an intermediate field between K and L, f: F → C is a field homomorphism such that f|_K = Φ. S = {(F, f): K ⊆ F ⊆ L, f: F → C, homomorphism, f|_K = Φ}.

• S ≠ ∅ because (K, Φ) ∈ S.
• We can define a partially order on S by declaring (F, f) ≤ (F’, f’) if F ⊆ F’ and f’|F = f.
• For a totally order subset {(F_α,fα)}_{α ∈ A} in S, an upper bound can be obtained as follows. Let F = $\cup_{α∈A} F_α$. It is easy to see that F is a field. Since the F_α’s are totally ordered, f: F → C defined by f(x) = f_α(x) where x ∈ F_α is obviously an upper bound field homomorphism.
• f is well defined. Suppose f(x) = f_α(x) where x ∈ F_α and x ∈ F_β, too (Shits happens 😄), the question is f_α(x) = f_β(x)?

By assumption the subset {(F_α,fα)}_{α ∈ A} is totally order ⇒ (F_α, f_α) ≤ (F_β, f_β) or (F_β, f_β) ≤ (F_α, f_α). If (F_α, f_α) ≤ (F_β, f_β) ⇒ [By our order definition, f_β|_Fα = f_α] f_β(x) = f_α(x) ∀x ∈ F_α and we are done. The argument in the second case is completely the same (aka mutatis mutandis).

• Let x ∈ K ⇒ x ∈ F_α ∀α ∈ A (recall (F, f)∈ S ⇒[By definition] K ⊆ F ⊆ L) ⇒ f(x) = f_α(x) = [f_α|_K = Φ] Φ(x), and therefore f|_K = Φ
• f is a field homomorphism. Let x ∈ F_α, y ∈ F_α’ ⇒ [There is total ordering] We can suppose x, y ∈ F_β ⇒ x·y ∈ F_β ⇒ f(x·y) = [x·y ∈ F_β] f_β(x·y) = [f_β is a field homomorphism] f_β(x)·f_β(y) = [x, y ∈ F_β, and f|_Fβ = f_β because (F, f) is obviously an upper bound on all the (F_α, f_α)’s] f(x)·f(y).

By Zorn’s lemma, S has a maximal element (F, σ): F is a field between K and L (K ⊆ F ⊆ L), with a homomorphism σ: F → C such that σ|_K = Φ. Futhermore, it is a maximal element, so it means that there is no extension of σ to a homomorphism from a larger intermediate field to C. Claim: F = L, that is, Φ is extended to a homomorphism L → C by σ

Let’s suppose for the sake of contradiction, F ≠ L ⇒ [K ⊆ F ⊆ L] ∃ a ∈ L, a ∉ F ⇒ F(a)/F is a finite extension of degree greater than 1. Then, we could extend σ to a homomorphism F(a) → C. Let p(x) be the minimal polynomial for a in F[x], so there is an F-isomorphism F(a) ≋ F[x]/⟨p(x)⟩.

Applying σ to the coefficients of p(x) gives a polynomial p^σ(x) ∈ C[x] ⇒ [C is algebraically closed] p^σ(x) has a root in C, say r.

Let’s define a ring homomorphism F[x] → C, acting as σ on F, and x → r. It sends p(x) to p^σ(r) = [r is a root of p^σ] 0, so we get an induced homomorphism F(x)/⟨p(x)⟩ → C acting as σ on F and [$\bar x$ = x + ⟨p(x)⟩ → r] sending $\bar x$ to r. Composing the isomorphism F(a) ≋ F[x]/⟨p(x)⟩ with this induced homomorphism F(x)/⟨p(x)⟩ → C gives us a homomorphism τ: F(a) → C acting as σ on F ⇒ (F, σ) ≤ (F(a), τ) ⊥ (F, σ) is a maximal element, F ≠ F(a) (a ∉ F).

τ = F-isomorphism, F(a) → F[x]/⟨p(x)⟩ composed with F(x)/⟨p(x)⟩ → C, $\bar x$ = x + ⟨p(x)⟩ → r acting as σ on F.

Theorem. Let K be a field and i: K → L be a homomorphism to a field L such that L/i(K) is an algebraic extension. If ϕ is a field homomorphism ϕ: K → C, and C is an algebraically closed field, then there is a field homomorphism σ : L → C such that σ ◦ i = ϕ (it makes the following diagram commute)

Proof.

Since “i” is a field homomorphism ⇒ i is injective ⇒ K ≋ i(K). We can use the same argument as before but using:

1. S = {(F, f): F field, i(K) ⊆ F ⊆ L, f∘i: F → C, homomorphism, f∘i = Φ}.
2. Define a partially order on S by declaring (F, f) ≤ (F’, f’) if F ⊆ F’ and f’|F = f.
3. For a totally order subset {(F_α,fα)}_{α ∈ A} in S, an upper bound can be obtained as follows. Let F = $\cup_{α∈A} F_α$, F is a field (since the F_α’s are totally ordered) f: F → C defined by f(x) = f_α(x) when x ∈ F_α.
4. By Zorn’s lemma, S has a maximal element (F, σ): F is a field between i(K) and L (i(K) ⊆ F ⊆ L), with a homomorphism σ: F → C such that σ∘i = Φ. Futhermore, it is a maximal element, so it means that there is no extension of σ to a homomorphism from a larger intermediate field to C. Claim: F = L ⇒ σ: L → C such that σ∘i = Φ (it is left to the reader as an exercise).

• A field F is algebraically closed if every non-constant polynomial f(x) ∈ F[x] has a zero in F. A field F is algebraically closed iff every non-constant polynomial in F[x] factors into linear polynomials over F[x]

Proof.

Assume F is algebraically closed, let f(x) ∈ F[x] be non-constant ⇒ ∃α ∈F: f(α) = 0 ⇒[Factor Theorem, F field, f ∈ F[x], α ∈ F is a zero or root of f, i.e., f(α) = 0 ↭ (x -α)|f(x)] f(x) = (x -α)g(x) for some g(x) ∈ F[x].

If g(x) is not constant ⇒ ∃β ∈ F: g(β) = 0, hence g(x) = (x -β)h(x) and f(x) = (x -α)(x -β)h(x) for some h(x) ∈ F[x]. If we continue this process, we can express f(x) as a product of linear polynomials.

• Corollary. Let F be an algebraically closed field, and let f(x) ∈ F[x] be irreducible. Then, f(x) is linear.

Proof. If f(x) is not linear, then we can write it as a product of more than one linear factor, which means that it is not irreducible

• Any algebraically closed field F has no proper algebraic extensions.

Proof.

Suppose for the sake of contradiction, E is a proper algebraic extension of F. Let α ∈ E an algebraic element, α ∉ F ⇒[Corollary. Let F be an algebraically closed field, and let f(x) ∈ F[x] be irreducible. Then, f(x) is linear] The irreducible polynomial of α, irr(α, F) ∈ F[x] must be linear, and since α is a zero of irr(α, F) we must have irr(α, F) = x - α ⇒[irr(α, F) = x - α ∈ F[x]] α ∈ F ⊥ Hence, E = F.

Theorem. All algebraic closures of a field are isomorphic. Let C₁ and C₂ be algebraic closures of a field K with embeddings i₁ : K → C₁ and i₂ : K → C₂ respectively, then there is a field isomorphism σ that makes the following diagram commute.

Proof. Since C₂ is algebraically closed and C₁ is an algebraic extension of i₁(K) ⇒ [i: K → L homomorphism, L/i(K) is an algebraic extension. ϕ field homomorphism: K → C, and C is an algebraically closed field, then there is a field homomorphism σ : L → C such that σ ◦ i = ϕ] There is a field homomorphism σ: C₁ → C₂ such that σ ◦ i₁ = i₂

The image σ(C₁) is an algebraically closed field that contains σ(i₁(K)) = i₂(K). Since C₂ is an algebraic extension of i₂(K) ⇒ C₂/σ(C₁) is an algebraic extension of an algebraically closed field ⇒ [Any algebraically closed field F has no proper algebraic extension] the extension C₂/σ(C₁) is trivial ⇒ σ(C₁) = C₂ ⇒ σ: C₁ → C₂ is not just a field homomorphism (injective), but a field isomorphism ⇒ σ ◦ i₁ = i₂ is a field isomorphism, and the diagram commute.

Exercise. Let p be a prime number, find the splitting field of X^p -2 over ℚ and its degree over ℚ.

Solution.

Let K be the splitting field fo x^p -2 over ℚ. Its roots are $ξ_p^i\sqrt[p]{2}∈\mathbb{R}$, where ξ_p is a primitive pth root of unity, 0 ≤ i ≤ p-1 ⇒ K = ℚ($ξ_p, \sqrt[p]{2}$), e.g., K = $ℚ(\sqrt[3]{2}, w)$ is the splitting field of x³ -2 over ℚ

By Eisenstein criteria X^p -2 is irreducible polynomial over ℚ, and the irreducible polynomial of ξ_p is not x^p -1 because it factors (x -1)(x^p-1 + x^p-2 + x² + x +1 ), but it is indeed (x^p-1 + x^p-2 + x² + x +1 ) that is irreducible (Corollary For any prime p, the pth cyclotomic polynomial Φ_p(x) = $\frac{x^p-1}{x-1}=x^{p-1}+x^{p-2}+···+x+1$ is irreducible over ℚ.) ⇒ [$\mathbb{Q}(\sqrt[p]{2}): ℚ$] = p, [ℚ(ξ_p): ℚ] = p -1.

n = [K : $\mathbb{Q}(\sqrt[p]{2})$][$\mathbb{Q}(\sqrt[p]{2}) : \mathbb{Q}$] = [K : $\mathbb{Q}(\sqrt[p]{2})$]·p ⇒ p | n and n ≤ p(p -1) that’s because K = $(\mathbb{Q}\sqrt[p]{2})(ξ_p)$ ⇒ [K : $\mathbb{Q}(\sqrt[p]{2})$] ≤ p-1.

Analogously, n = [K : ℚ(ξ_p)][$\mathbb{Q}(ξ_p) : \mathbb{Q}$] = [K : ℚ(ξ_p)]·(p-1) ⇒ (p-1) | n. Then, p | n, (p-1) | n, n ≤ p(p -1), p prime ⇒ n = p(p-1).

Proposition. Let K/F be an algebraic extension, let σ: K → K be an F-homomorphism. Then, σ is an isomorphism. Every F-homomorphism between K to itself is an isomorphism.

Proof.

By assumption σ is an F-homomorphism ⇒ it is injective [σ(a) = σ(b) ⇒ σ(a)-σ(b) = σ(a -b) = 0 = σ(0). If u = (a-b) = 0 ⇒ we are done, a = b. Otherwise, u ≠ 0 ⇒ σ(u)σ(u^-1) = σ(1) = 1, but that means σ(u)σ(u^-1) =[σ(u) = σ(a-b) = 0] 0σ(u^-1) = 1 ⊥

Let α ∈ K be an arbitrary element. K/F is an algebraic extension, therefore α is algebraic over F, so let us consider its irreducible polynomial f ∈ F[x] over F. Let A = {α = α₁, α₂, ···, α_n} be the set of all roots of f in K (it may not be the set of all roots of f -f does not necessarily splits completely in K-, but at least there is an element, α itself).

⇒ Theorem [K, L be two extension fields of F. α ∈ K is algebraic over F. Let σ: K → L be an F-homomorphism of fields. Then, σ(α) is algebraic over F, too and its irreducible polynomial over F is the same as the irreducible polynomial of α over F] σ(α_i) = α_j, ∀i, j = 1,···, n, and therefore σ(A) ⊆ A. Let’s restrict σ to A, σ_A = σ|A, it is well defined because σ(A) ⊆ A, it is injective because σ is an injective map from K to K, and it is surjective because it is an injective map from a finite map to itself ⇒ ∃α_i ∈ A: σ(α_i) = α₁ = α, and therefore σ: K → K is surjective (∀α∈ K, ∃α_i ∈ A ⊆ K, σ(α_i) = α₁ = α), hence an isomorphism∎

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.