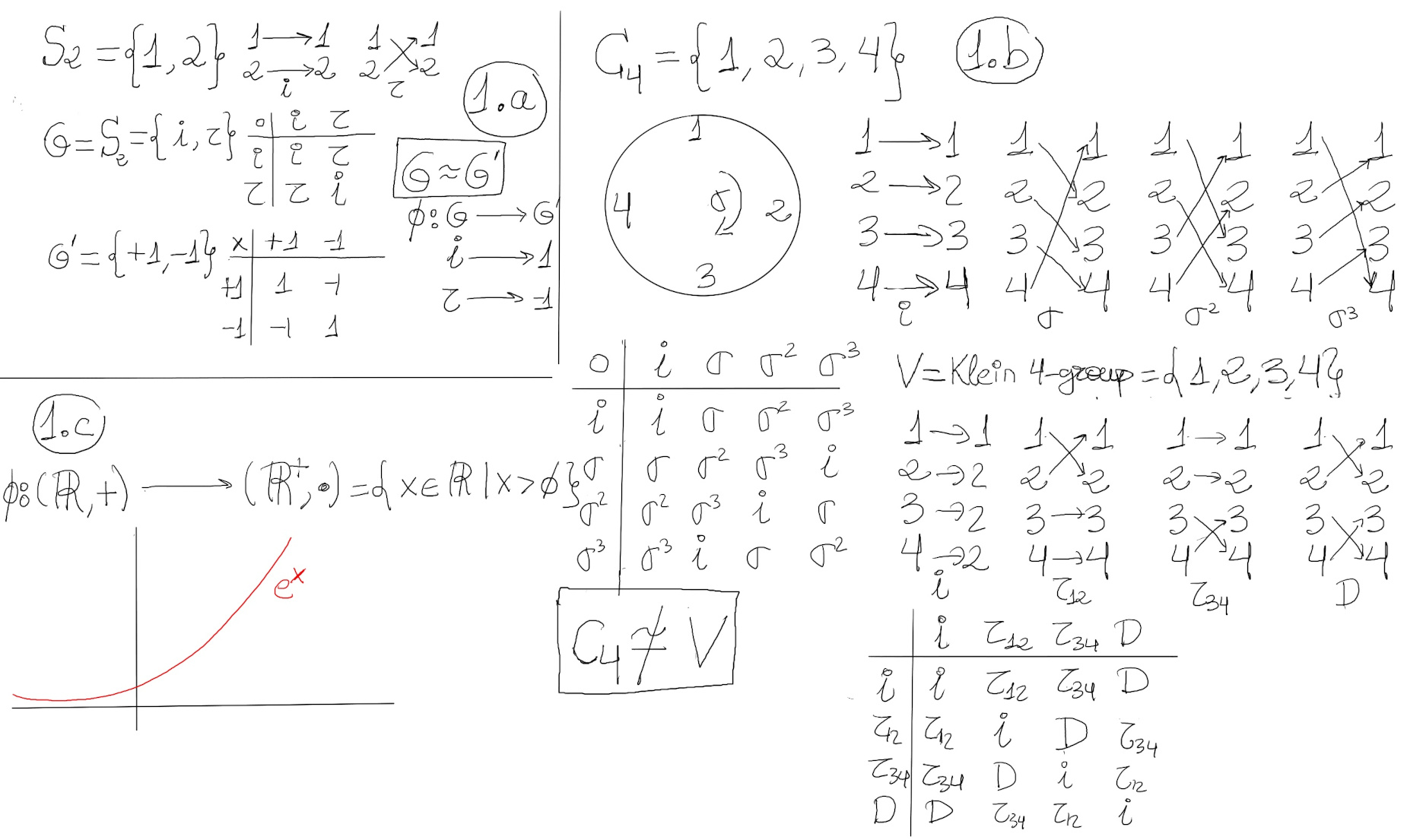Don’t worry if people think you’re crazy. You are crazy. You have that kind of intoxicating insanity that lets other people dream outside of the lines and become who they’re destined to be, Jennifer Elisabeth, Born Ready: Unleash Your Inner Dream Girl.
Let (A, *) and (B, ⋄) be two binary algebraic structures. A homomorphism is a structure-preserving map between two algebraic structures of the same type (groups, rings, fields, vector spaces, etc.) or, in other words, a map ϕ: A → B, such that ∀x, y ∈ S : ϕ(x ∗ y) = ϕ(x) ⋄ ϕ(y).
Notice that ϕ may not be one to one (injection), nor onto (surjection). An isomorphism is a bijective homomorphism, i.e., one-to-one and onto. In other words, let (S, *) and (S’, ⋄) be two binary algebraic structures of the same type. An isomorphism of S with S' is a 1-1 function ϕ mapping from S onto S′ such that the homomorphism property holds: ∀x, y ∈ S : ϕ(x ∗ y) = ϕ(x) ⋄ ϕ(y). S and S’ are said to be isomorphic binary structures and we denote or write it by S ≃ S’ or S ≋ S'.
In particular, two groups (G, *) and (G', ⋄) are isomorphic if there exist a bijective homomorphism, i.e., a one-to-one and onto map Φ: G → G’ such that the group operation is preserved, that is, ∀x, y ∈ G : ϕ(x ∗ y) = ϕ(x) ⋄ ϕ(y). Isomorphic groups are equivalent, that is, they share the same algebraic and group theoretic properties.
Examples
- For any group G, G ≋ G.
- S2 is isomorphic to C2 (it is also denoted as ℤ2 and ℤ/2ℤ) = {1, -1}, the cyclic group of order 2, i.e., the multiplicative group comprising 1 and -1 (1.a).
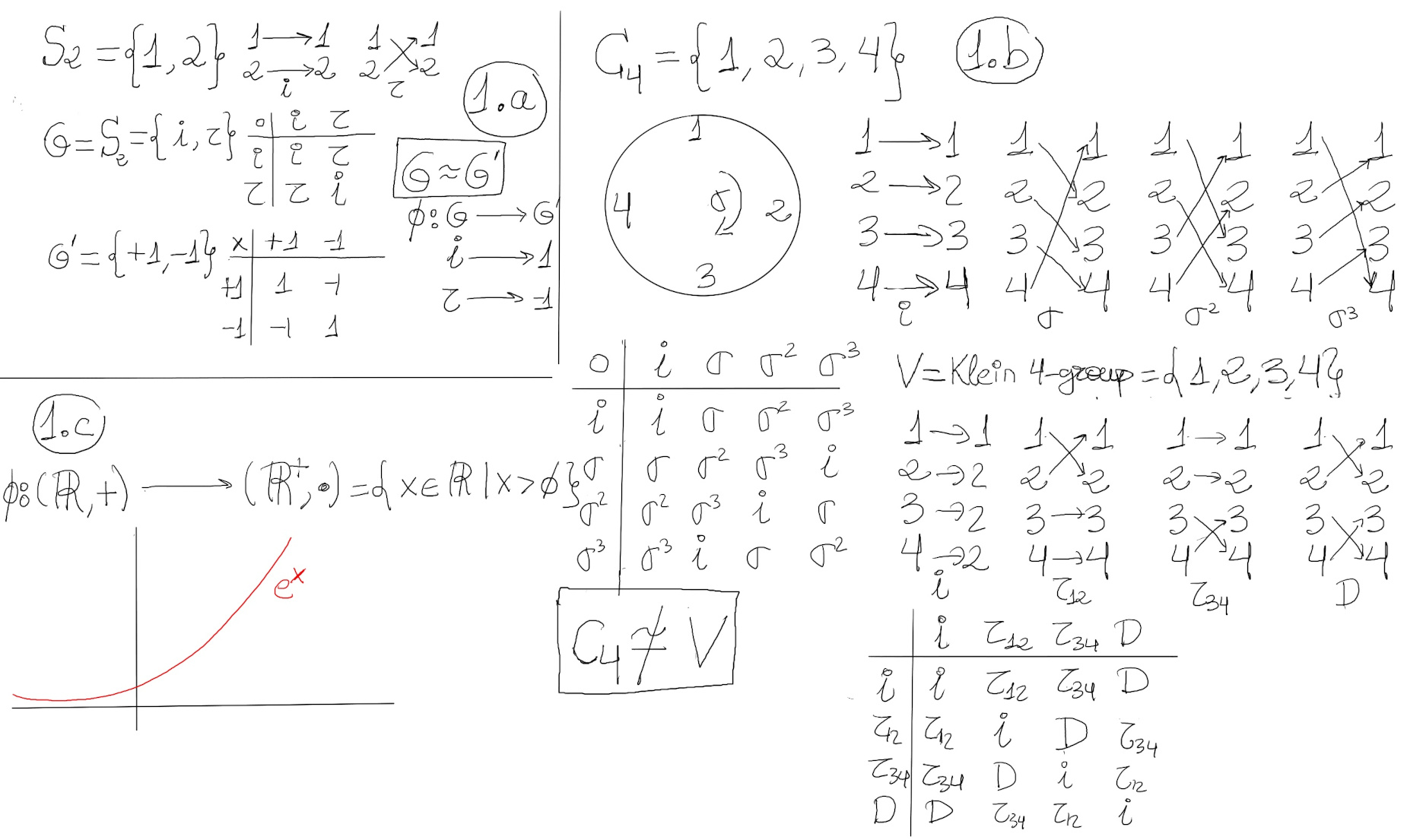
- ℤ4 = {0, 1, 2, 3}, ℤ4 = ⟨1⟩, ℤ4 ≋ ⟨i⟩ = {1, -1, i, -i}, Φ: ℤ4 → ⟨i⟩ defined by Φ(n) = in, 0 → 1, 1 → i, 2 → -1, 3 → -i, so it is obviously one-to-one and onto. Besides, Φ(m + n) = im+n = im·in = Φ(m)·Φ(n).
- Let C4 = ⟨σ⟩ = {i, σ, σ2, σ3}, i = (), σ = (1234) -1.b.- The Klein 4-group K4 and the cyclic group of order 4, C4, are not isomorphic because the Klein four-group is a group with four elements, in which each element is self-inverse (composing it with itself produces the identity). However, σ·σ = σ2 ≠ identity. Suppose for the sake of contradiction, Φ: C4 → K4 isomorphism ⇒ Φ(σ2) = Φ(σ)·Φ(σ) = Φ(σ)2 = [Each element in K4 has order 2] id. Φ(i) = Φ(i·i) = Φ(i)2 = [Each element in K4 has order 2] id. Therefore, Φ(σ2) = Φ(i) = id ⊥ Φ is an isomorphism (Φ is not one to one).
If Φ: G → G’ is a group homomorphism, then ∀a ∈ G, |Φ(a)| = |a|. In particular, σ = (1234), |σ| = 4, but K4 has no elements of order 4⊥
- (ℤ, +) is isomorphic to (2ℤ, +) where 2ℤ = {2n | n ∈ ℤ}.
- First, we define the function ϕ: ℤ → 2ℤ, ϕ(n) = 2n.
- Let’s see that ϕ is a one-to-one function. ϕ(n)=ϕ(m) ⇒ 2n = 2m ⇒ n = m.
- ϕ is onto S’. ∀n ∈ 2ℤ, then ∃m ∈ ℤ: n = 2m, ϕ(m) = 2m = n.
- ϕ(m+n) = 2(m+n) = 2m + 2n = ϕ(m) + ϕ(n).
- (ℝ, +) is isomorphic to (ℝ+, ·). Fig. 1.c.
- First, we define the function ϕ: ℝ → ℝ+. ϕ(x) = ex.
- Let’s see that ϕ is a one-to-one function. ϕ(n)=ϕ(m) ⇒ en = em ⇒ ln(en) = ln(em) ⇒ n = m.
- ϕ is onto S’. ∀r’ ∈ ℝ+, ∃r ∈ ℝ such that r = ln(r’), and obviously ϕ(r) = er = eln(r’) = r'.
- ϕ(r+s) = er+s = eres = ϕ(r)ϕ(s).
- Conversely, we could have demonstrated that (ℝ+, ·) is isomorphic to (ℝ, +).
- First, we define the function ϕ: ℝ+ → ℝ. ϕ(r) = ln(r).
- Let’s see that ϕ is a one-to-one function. ϕ(n)=ϕ(m) ⇒ ln(n) = ln(m) ⇒ eln(n) = eln(m) ⇒ n = m.
- ϕ is onto S’. ∀r ∈ ℝ, ∃r’ ∈ ℝ+ such that r’= er, and obviously ϕ(r’) = ln(er) = r.
- ϕ(r+s) = ln(r+s) = ln(r) + ln(s) = ϕ(r) + ϕ(s).
- The circle group, $\Tau$ = {z ∈ ℂ: |z|=1} is a proper subgroup of ℂ*. It is the multiplicate group of all complex numbers with absolute value 1, that is, the unit circle in the complex plane. It has infinite order.
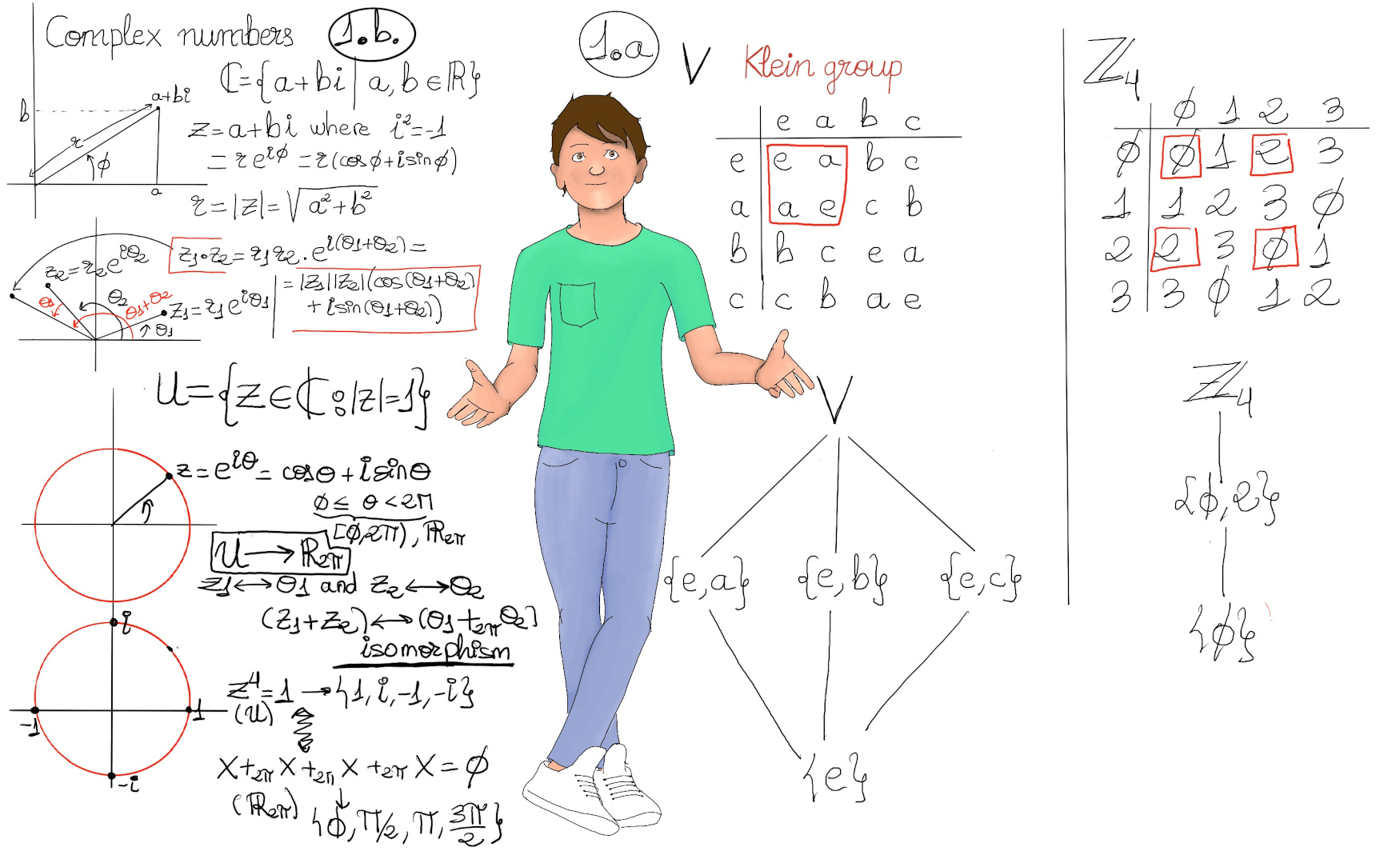
There is an homomorphism between ℂ* and $\Tau$, ϕ: ℂ* → $\Tau$, ϕ(reiθ) = eiθ.
Let z = reiα, w = seiβ ⇒ ϕ(zw) = ei(α+β) = (eiα)(eiβ) = ϕ(z)ϕ(w), but it is not obviously onto because for every point in the unit circle, there are infinite number of complex numbers which map to it.
However, there is an isomorphism between U = $\Tau$ and ℝ2π with addition modulo 2π. z1 = eiθ1 (z1 ↔ θ1), z2 = eiθ2 (z1 ↔ θ1) then z1 + z2 ↔ θ1 + θ2.
In other words, the algebraic properties of U and ℝ2π are the same, e.g., z4 = 1 has four solutions in U, namely 1, i, -1, -i, and x +2π + x +2π + x +2π x = 0 has four solutions in ℝ2π (0, π, π/2, 3π/2), too.
-
Let G be a cyclic group with generator a. If the order of G is infinite, then G is isomorphic to (ℤ, +). Otherwise, G is isomorphic to (ℤn, +n) As a result, U10 ≋ ℤ4, U7 ≋ ℤ6, and U5 ≋ ℤ4 because U10 and U5 are both cyclic of order 4, and U7 is cyclic of order 6. Therefore, for every n, there is really only one cyclic group of order n (up to isomorphism).
G = ⟨a⟩. If (G, ·) is infinite, ∀m ∈ ℤ, m ≠ 0, am ≠ e, Φ: (G, ·) → (ℤ, +), Φ(am) = m, Φ is an isomorphism. If (G, ·) is finite, ∃m ∈ℤ: am = e. Let n be the smallest positive integer such that an = e, then Φ: (G, ·) → (ℤn, +n) defined by Φ(ai) = i is an isomorphism.
-
There is no isomorphism from (ℚ, +) to (ℚ*, ·)
Proof by contradiction: Suppose that Φ were such a mapping, there would be an a ∈ ℚ: Φ(a) = -1 ⇒ -1 = Φ(a) = Φ(a/2 + a/2) = Φ(a/2)Φ(a/2) = Φ(a/2)2 ⇒ there would be an a ∈ ℚ: -1 = Φ(a/2)2 ⊥
- There is no isomorphism from U12 to U10.
U12 = {1, 5, 7, 11}. Assume there is an isomorphism Φ: U10 → U12, Φ(9) = Φ(3·3) = Φ(3)Φ(3) = (Φ(3))2 = [Observe that x2 = 1 ∀x ∈ U12] 1. Similarly, Φ(1) = Φ(1·1) = Φ(1)Φ(1) = (Φ(1))2 = 1. Therefore, Φ(9) = Φ(1), that is, Φ is not one to one, ⊥
- Let G = SL(2, ℝ) the group of two by two real matrices with determinant one. Let M be any arbitrary two by two matrix with determinant one and let’s define a mapping ΦM: SL(2, ℝ) → SL(2, ℝ), ΦM(A) = MAM-1. ΦM is indeed an isomorphism:
- ΦM(A) = MAM-1 ∈ SL(2, ℝ)? det(MAM-1) = (det M)(det A)(det M)-1 = 1 · 1 · 1 = 1.
- ΦM(A) = ΦM(B) ⇒ MAM-1 = MBM-1 ⇒ [∴ SL(2, ℝ) is a group and cancellation laws do apply] A = B.
- B ∈ SL(2, ℝ), we must find a matrix A: ΦM(A) = MAM-1 = B, but this is really trivial, it is indeed A = M-1BM.
- ΦM(AB) = M(AB)M-1 = MA(M-1M)BM-1 = (MAM-1)(MBM-1) = ΦM(A)ΦM(B).
- Let’s define Φ :D6 → S3, Φ(r) = a, Φ(s) = b. It is an homomorphism.
- S3 is generated by a and b (it is left as an exercise) ⇒ Φ is surjective.
- |D6| = |S3| = 6 ⇒ Φ is isomorphism, D6 ≋ S3.
Cayley’s Theorem
Cayley’s Theorem. Every group G is isomorphic to a subgroup of a symmetric group. In particular, every finite group is isomorphic to a subgroup of Sn.
Recall: The symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group Sn defined over a finite set of n symbols consists of all the permutations that can be performed on the n symbols.
Proof.
- ∀g ∈ G, consider the function fg: G → G, defined by fg(x) = g · x. By the existence of inverses, fg has an inverse fg-1, defined as fg-1(x) = g-1·x.
Note that ∀x ∈G, fgfg-1(x) = fg(fg-1(x)) = fg(g-1·x) = g·(g-1·x) = [Associative] (g·g-1)·x = e·x = x. Similarly, ∀x ∈G, fg-1fg(x) = x
Theorem. A function is bijective if and only if has an inverse. Therefore, fg is bijective ⇒ fg is a permutation of G ⇒ fg ∈ Sym(G).
- The set K = {fg: g ∈ G} is a subgroup of Sym(G) that is isomorphic to G. Let’s prove K ≤ Sym(G).
- Associative. The operation of function composition is associative.
- Close under function composition. ∀g, h, x ∈ G: fg·fh(x) = fg(fh(x)) = fg(h·x) = g·(h·x) = [G group. Associative] (g·h)·x = fgh(x), gh ∈ G (G is a group, ∀g, h, gh ∈ G) ⇒ fgh ∈ K.
- fe is the identity.
- ∀g ∈ G, (fg)-1 = fg-1 (it was previously proven).
- We are going to establish a map Φ between G and K = {fg: g ∈ G}.
-
First, we define the function Φ: G → K, Φ(g) = fg.
-
Φ is a group homomorphism, Φ(g·h) = fg·h = [*1] fg·fh = Φ(g)·Φ(h)
[*1]fg·fh(x) = fg(fh(x)) = fg(h·x) = g·(h·x) =[(G, ·) group ⇒ Associativity] (g·h)·x = fg·h(x) ∀x ∈G
-
Φ(g) = Φ(h) ⇒ fg = fh ⇒ ∀x ∈ G, fg(x) = fh(x) ⇒ ∀x ∈ G, g·x = h·x. The identity element, e ∈ G ⇒ g·e = h·e ⇒ g = h ⇒ Φ is one-to-one.
-
By the way K = {fg: g ∈ G} was constructed, Φ is obviously onto∎
Definition. The map Φ in the proof of Cayley’s Theorem is the left representation of G.
Examples of the regular group representation.
- (ℤ2, +mod2) = {0, 1}. 0 corresponds to the identity permutation → (), 1 → (12).
- (ℤ3, +mod3). 0 corresponds to the identity permutation, 1 → (123) -f1(x) =[Additive notation] 1 +mod 3 x-, and 2 → (132) -f2(x) = 2 +mod 3 x-.
- ℤ4, +mod4. 0 corresponds to the identity permutation, 1 → (1234), 2 → (13)(24), and 3 → (1432).
- Let’s calculate a group of permutations that is isomorphic to U8 = {1, 3, 5, 7}, U’8 = {T1, T3, T5, T7}. Observing Cayley's Tables, it is obvious that U8 and U'8 are algebraically or structurally the same.
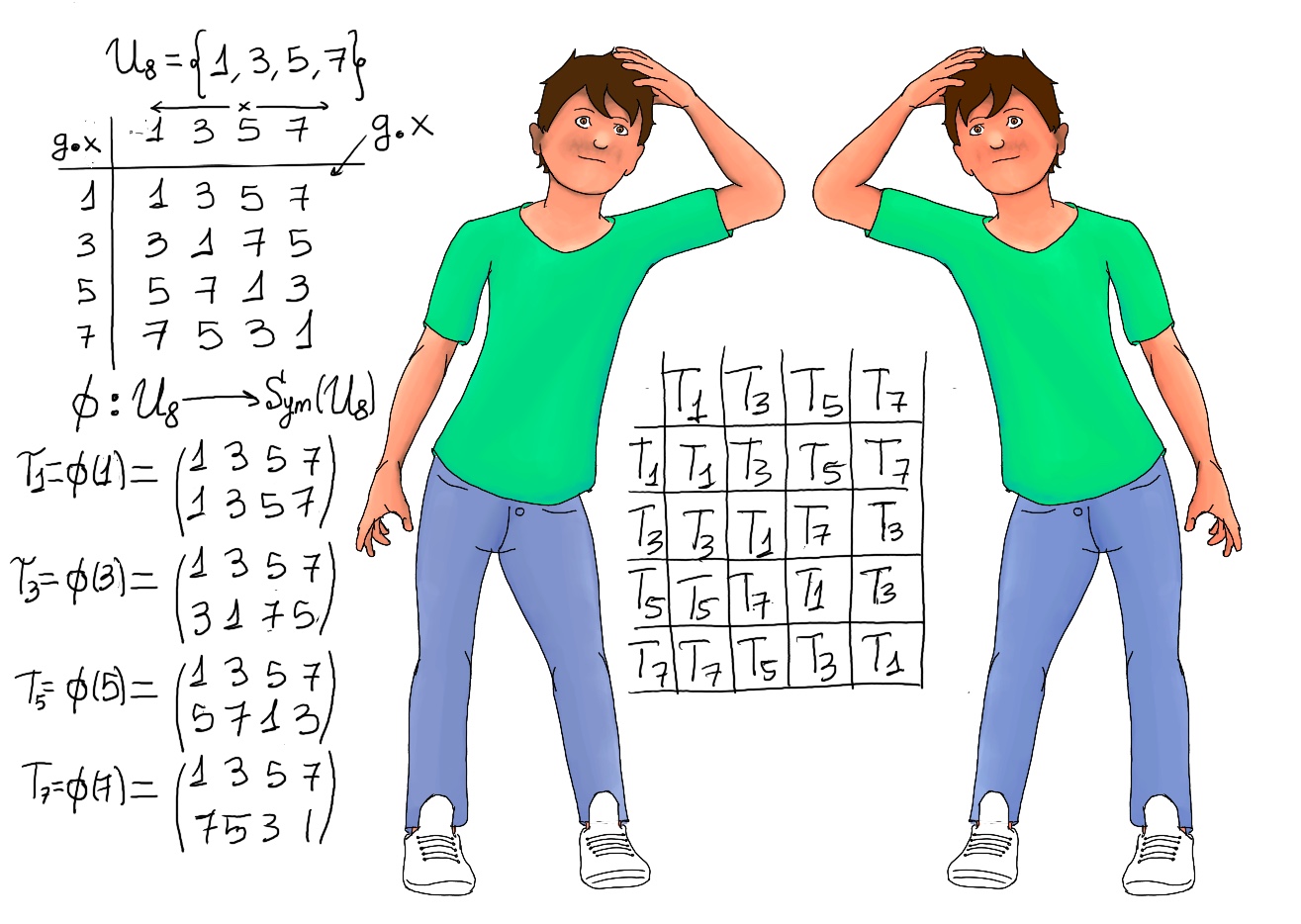
- Klein four-group {e, a, b, c} corresponds to e, (12)(34) -fa(x) = a·x, fa(e) = a, fa(a) = e, fa(b) = c, fa(c) = a, (ea)(bc)-, (13)(24), and (14)(23).
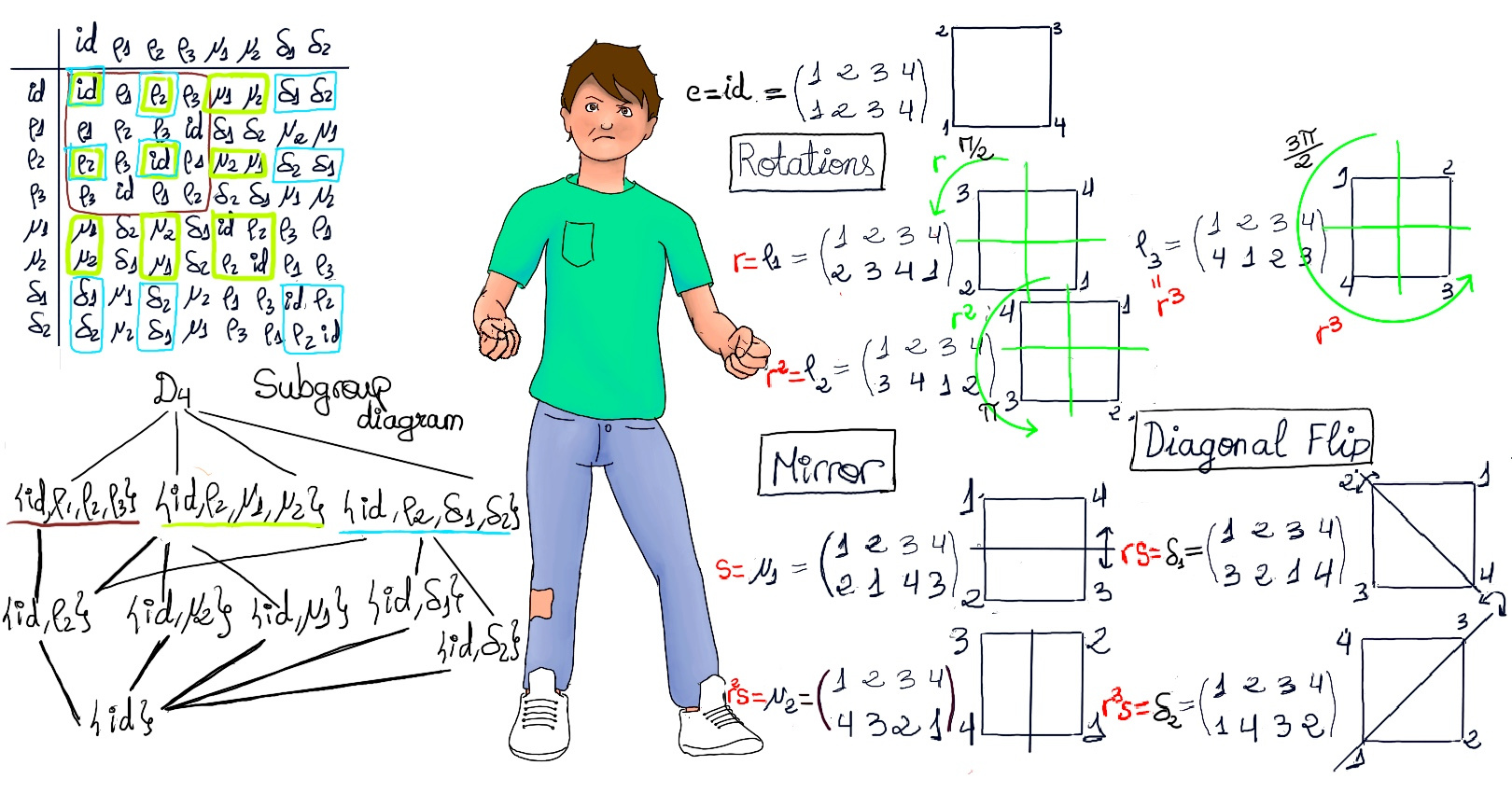
- D6 = {id (e), rotations (ρ1 -90° around the center anticlockwise-, ρ2 -180°-, and ρ3 -270°-), reflections or mirror images in the x -horizontal- and y -diagonal- axes (μ1, μ2), and reflections in the diagonal δ1 and δ2} = {e, s, rs, r2s, r2, r3s, r, r3 where rs = sr3} → e, (12)(35)(46) -fs(x) = s·x, fs(e) = s, fs(s) = e, fs(rs) = srs = ssr3 = r3, fs(r3) = sr3 = rs, fs(r2s) = sr2s = srrs = s(rs)r3 = ssr3r3 = r2, fs(r2) = sr2 = sr2r4 = sr3r3 = rsr3 = r2s -, (13)(26)(45), (14)(25)(36), (156)(243), (165)(234).
Bibliography
This content is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. This post relies heavily on the following resources, specially on
NPTEL-NOC IITM, Introduction to Galois Theory, Michael Penn, and Contemporary Abstract Algebra, Joseph, A. Gallian.
- NPTEL-NOC IITM, Introduction to Galois Theory.
- Algebra, Second Edition, by Michael Artin.
- LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
- Field and Galois Theory, by Patrick Morandi. Springer.
- Michael Penn (Abstract Algebra), and MathMajor.
- Contemporary Abstract Algebra, Joseph, A. Gallian.
- Andrew Misseldine: College Algebra and Abstract Algebra.