
|
 |
 |
|
 |
For many weeks I was absorbed in improving Judith. I didn’t want to think about my next medical revision, and yet being stubbornly selective about the reality I am willing to accept comes with a high price tag. You know, for whatever unexpected, unholy, and mysterious reason that I cannot fathom, it does not change the facts and finally the day arrived …
“Body scans show that your thyroid cancer has indeed spread to your lungs…” “If you can dream it, you can do it, bullshit! Anything is possible if you believe in yourself, bullshit! You deserve whatever you want, all the good things that happen to you, bullshit! Fuck them all, their books, most psychologists and life coaches, and all their uplifting, feel good, and deceiving bullshit. Let them all burn slowly and merciless in hell for all eternity and that’s obviously a long, very long time,” I thought bitterly. Apocalypse, Anawim, #justtothepoint.
A field homomorphism between two fields E and F is a function f: E → F such that ∀x, y ∈ E: f(x + y) = f(x) + f(y), f(xy) = f(x)f(y), f(1) = 1. It implies: f(0) = 0, f(x-1) = f(x)-1, and f is injective.
Let K/F and L/F be two extensions of F. An F-homomorphism of extensions of F is a field homomorphism σ: K → L such that σ(a) = a ∀a ∈F.
Proposition. Let F be a field, let K and L be two extension fields of F. Suppose α ∈ K is algebraic over F. Let σ: K → L be an F-homomorphism of fields. Then, σ(α) is algebraic over F, too, and its irreducible polynomial over F is the same as the irreducible polynomial of α over F, e.g., K = $\mathbb{Q}(\sqrt{2})→ L = \mathbb{C}, F = \mathbb{Q}$. Then we know that $σ(\sqrt{2})=\sqrt{2}~ or~ -\sqrt{2}$ because its irreducible polynomial x2 -2 has only these two roots.
Proof:
α is algebraic over F ⇒ α is a root of some non-zero polynomial with coefficients in F, say f ∈ F[x], let f(x) be anxn + an-1xn-1 + ··· + a1x + a0, where ai ∈ F, let σ(α)= β [σ: K → L] ∈ L
f(β) = anβn + an-1βn-1 + ··· + a1β + a0 = [σ(α) = β ∈ L] anσ(α)n + an-1σ(α)n-1 + ··· + a1σ(α) + a0 = [σ is an homomorphism] anσ(αn) + an-1σ(αn-1) + ··· + a1σ(α) + a0 = [σ is an F-homomorphism, σ(ai) = ai ∀i] σ(anαn + an-1αn-1 + ··· + a1α + a0) = [α is a root of f] σ(0) = 0, therefore β is a root of f ⇒ β is algebraic over the same irreducible polynomial of α.
Corollary. If K, L are field extensions of ℚ, then any field homomorphism between K and L is a ℚ-homomorphism.
Example. Let K = L = ℚ($\sqrt{2}, \sqrt{3}$), σ defined by $\sqrt{2} → -\sqrt{2}, \sqrt{3} → \sqrt{3}$ is a field homomorphism, so it is a ℚ-homomorphism, it is an ℚ($\sqrt{3}$)-homomorphism, but it is not an ℚ($\sqrt{2}$)-homomorphism because $σ(\sqrt{2}) = -\sqrt{2}$ is not a root of x2-2.
Give K a field, a polynomial p(x) ∈ K[x]. We want to find an extension field L of K such that “all roots of p are in L”, more precisely p factors into linear factors in L[x]. Futhermore, we want to find the “smallest extension”, i.e., one that is generated by the roots of p. L is called the splitting field of K.
Examples
Let α = x + ⟨x2 +1⟩ and -α be f(x)’s root, then (x2 +1) = (x -α)(x +α).
Let’s check this. Consider (x -α)(x +α) = x2 -α2 = x2 -(x2 + ⟨x2 +1⟩)= 0 + ⟨x2 +1⟩ ⇒ [x2 + 1 + ⟨x2 +1⟩ = 0 + ⟨x2 +1⟩ ⇒ -1 + ⟨x2 +1⟩ = x2 + ⟨x2 +1⟩ and we could abuse notation and identify -1 and -1 + ⟨x2 +1⟩, an element with its coset] (x -α)(x +α) = x2 -(x2 + ⟨x2 +1⟩)= x2 -(-1 + ⟨x2+1⟩) = x2 +1. Thus, x2 +1 can be written as a product of linear factors in some extension of ℚ. Splitting field is one such extension in which a polynomial is reduced to linear factors.
p(x) = x2 + a1x + a0 = 0, a0, a1 ∈ K. Suppose p is irreducible. L = K[x]/⟨p⟩ is a field and contains a root of p, say α. Futhermore, p = (x -α)(x - β) and doing some very basic calculations we know that α + β = -a1 ∈ K ⇒[By assumption, α ∈ L] β ∈ L, so L contains all roots of p, i.e., L is a splitting field.
f(x) = x5 + 2x2 + 2x + 2 ∈ ℤ3[x]. The irreducible factorization of f over ℤ3[x] is (x2 +1)(x3 +2x +2). Therefore, we have two field extensions in which f has a root: ℤ3[x]/⟨x2 +1⟩ and ℤ3[x]/⟨x3 +2x +2⟩.
Let f(x) be a polynomial in F[x] of degree ≥ 1. Then, an extension K of F is called a splitting field of f(x) over F if:
Let f(x) = x3 -1 be the minimal polynomial over ℚ. We know x = 1 is its root ∴ (x3 -1) = (x -1)(x2 + x + 1). Let p(x) = x2 + x + 1 be the minimal polynomial over ℚ, having “w” as it root ∴ Q[x]/⟨x2 + x + 1⟩ ≋ ℚ(w), and [ℚ(w):ℚ] = degree of minimal polynomial of w over ℚ = degree of x2 + x + 1 = 2, and the elements in its basis are {1, w}. Hence, ℚ(w) forms the splitting field of polynomial f(x) over ℚ.
If deg(p(x)) = n, and u is a root of this polynomial, the element of the basis are {1, u, u2, ···, un-1}
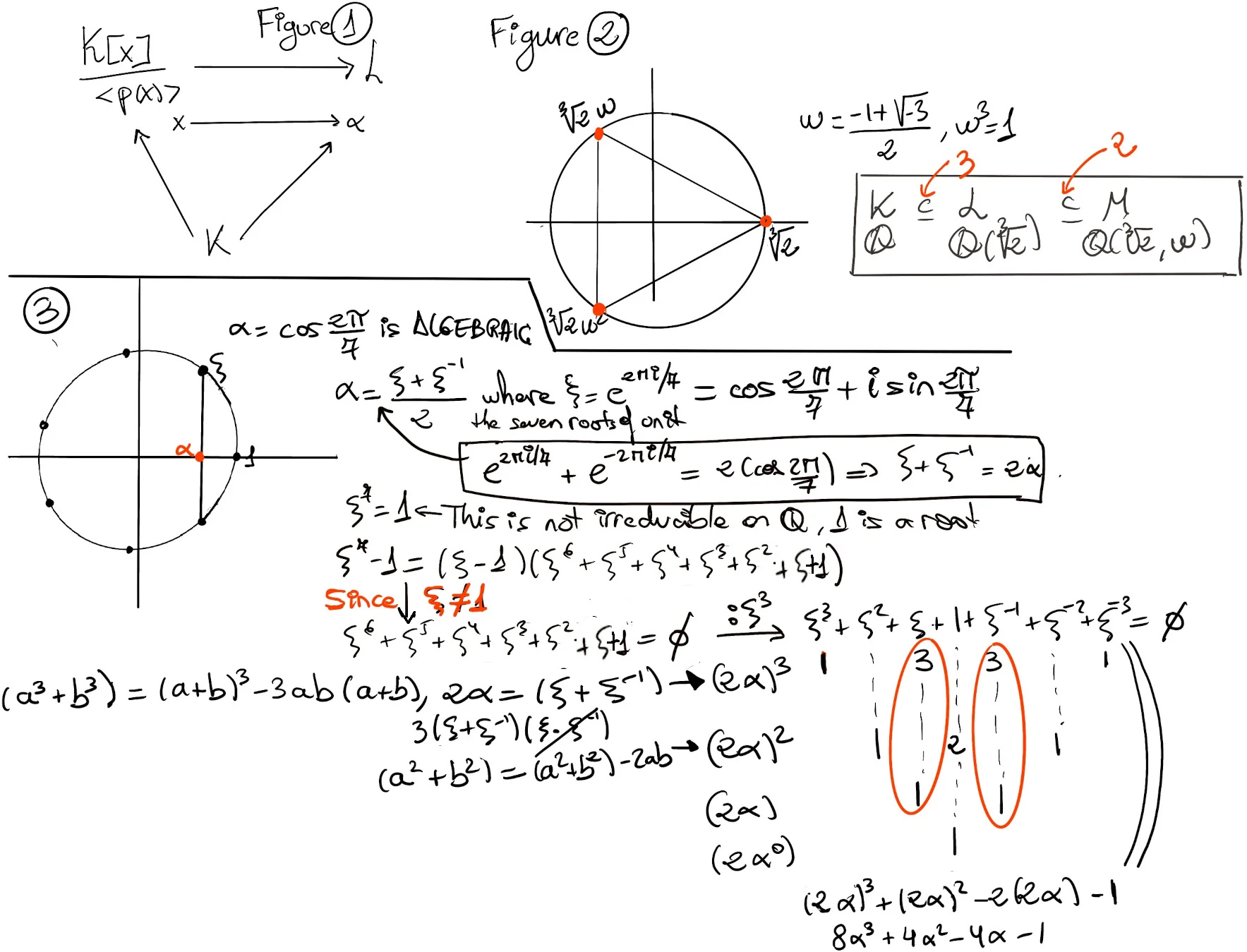
a3-b3=(a-b)(a2 + ab +b2), a = x, b = $\sqrt[3]{2}$, we get $x^3-2=(x-\sqrt[3]{2})(x^2+\sqrt[3]{2}x+\sqrt[3]{2}^2)$
p = $x^3-2=(x-\sqrt[3]{2})(x^2+\sqrt[3]{2}x+\sqrt[3]{2}^2),~ (x^2+\sqrt[3]{2}x+\sqrt[3]{2}^2)$ is irreducible over L. Let M = L[y]/⟨$(y^2+\sqrt[3]{2}y+\sqrt[3]{2}^2)$⟩. Therefore, K = ℚ ⊆ L (= ℚ($\sqrt[3]{2}$)) ⊆ M (= ℚ($\sqrt[3]{2}, w$)), and [M: K] = [M:L]·[L:K] = 3·2 = 6.

Because of cos(2θ) = 2cos2θ -1 ⇒ cos(4π⁄7) = 2(cos2π⁄7)2 -1, so if we add a root (say α = cos(2π⁄7)) of the polynomial p, then it automatically adds the other roots, and therefore ℚ[x]/⟨p(x)⟩ is the splitting field of p and its degree over ℚ is 3.
Let us consider f(x) = x4 -x2 -2 = (x2 -2)(x2 + 1) over the rational numbers ℚ. The zeros of f(x) are to be found in ℂ, namely $±\sqrt{2}, ±i$. Therefore, a splitting field f(x) over ℚ is ℚ$(\sqrt{2}, i) = ℚ(\sqrt{2})$(i) = {α + βi | α, β ∈ ℚ($\sqrt{2}$)} = {(a + b$\sqrt{2}$) + (c + d$\sqrt{2}$)i | a, b, c, d ∈ ℚ}
Show that the degree of the extension of the splitting field of f(x) = x3 - 2 ∈ ℚ[x] is 6.
By Eisentein’s criterion, f(x) is irreducible over ℚ because it exists p = 2 such that 2 | a0 = -2, 2 | a1 = 0, 2 | a2 = 0, 2 ɫ a3 = 1, 2 ɫ a02 = 4 ⇒ f(x) is irreducible over ℚ ⇒ ⟨x3 -2⟩ is a maximal ideal, ℚ[x]/⟨x3 -2 ⟩ ≋ ℚ($\sqrt[3]{2}$) (where $\sqrt[3]{2}$ is the root of x3 -2) is a field, and [ℚ($\sqrt[3]{2}$) : ℚ] = 3 because degree(x3 -2) = 3.
As one of the root of x3 - 2 is $\sqrt[3]{2}$ ⇒ (x-$\sqrt[3]{2}$) is a factor. Using long division we get (x3 -2) = (x-$\sqrt[3]{2}$)(x2 + $\sqrt[3]{2}$x + 2$\sqrt[3]{2^2}$)
Let p(x) = (x2 + $\sqrt[3]{2}$x + 2$\sqrt[3]{2^2}$). If α, $\bar α$ are the roots of p(x), then, ℚ($\sqrt[3]{2}$)[x]/⟨p(x⟩⟩ ≋ ℚ($\sqrt[3]{2}$, α). Since the degree of the minimal polynomial over α = deg(p(x)) = 2, then [ℚ($\sqrt[3]{2}$, α) :ℚ($\sqrt[3]{2}$)] = 2. Hence, [ℚ($\sqrt[3]{2}$, α) : ℚ] = [ℚ($\sqrt[3]{2}$, α) : ℚ($\sqrt[3]{2}$)] · [$\sqrt[3]{2}$) : ℚ] = 2 x 3 = 6, because the basis of ℚ($\sqrt[3]{2}$) = {1, $\sqrt[3]{2}$, $\sqrt[3]{2^2}$} and the basis of ℚ($\sqrt[3]{2}$, α) = {1, α}.
The basis elements of ℚ($\sqrt[3]{2}$, α) are {1, $\sqrt[3]{2}$, $\sqrt[3]{2^2}$, α, α·$\sqrt[3]{2}$, α·$\sqrt[3]{2^2}$, so any element of ℚ(21/3, α) is a linear combination of these six elements.

Theorem. Existence of Splitting Fields. Let F be a field and let f(x) be a non-constant polynomial of F[x]. Then, there exists a splitting field E for f(x) over F, e.g., x2 + 1 ∈ ℚ[x] splits over ℂ and ℚ(i).
Proof.
Let’s apply induction on the degree of f(x), say n = deg(f(x))
If n = 1, i.e., deg(f(x)) = 1 ⇒ f(x) is a linear polynomial. Hence, the splitting field of f(x) is F itself.
Let’s assume the result holds true for all polynomials with degree less than n, i.e., all polynomials with degrees n-1, n-2, ···, 2, and 1 have a splitting field over F. Of course, we are going to use strong induction.
Recall. Krnoecker’s Theorem. Existence of extension. Let F be a field and let f(x) be a non-constant polynomial in F[x]. Then, there exists an extension E of F in which f(x) has a root or zero.
We know, every non-constant polynomial has an extension field E having a root, say a1.
Then, we can write our non-constant polynomial f(x) = (x -a1)g(x), where g(x) ∈ E[x] and deg(g(x)) < deg(f(x)) ⇒ [By induction on g(x)], there is an extension field K of g(x) over E in which all roots, say a2, ···, an of g(x) are available, g(x) = (x -a2)(x -a3) ··· (x -an), hence f(x) = (x -a1)g(x) = (x -a1)(x -a2) ··· (x -an), i.e., K = E(α2, ···, αn) = F(α1, α2, ···, αn) is the splitting field of f(x) over F∎
Theorem. Let F be a field and let p(x) ∈ F[x] be an irreducible polynomial over F, deg(p(x)) = n. If a is a root of p(x) in some extension E of F, then F(a) is isomorphic to F[x]/⟨p(x)⟩, F(a) ≋ F[x]/⟨p(x)⟩. Moreover, F(a) is a vector space over F with a basis {1, a, ···, an-1}, i.e., every member of F(a) can be written in the form cn-1an-1 + cn-2an-2 + ··· + c1a + c0, where c0, c1, ···, cn-1 ∈ F (Figure 1.g.)
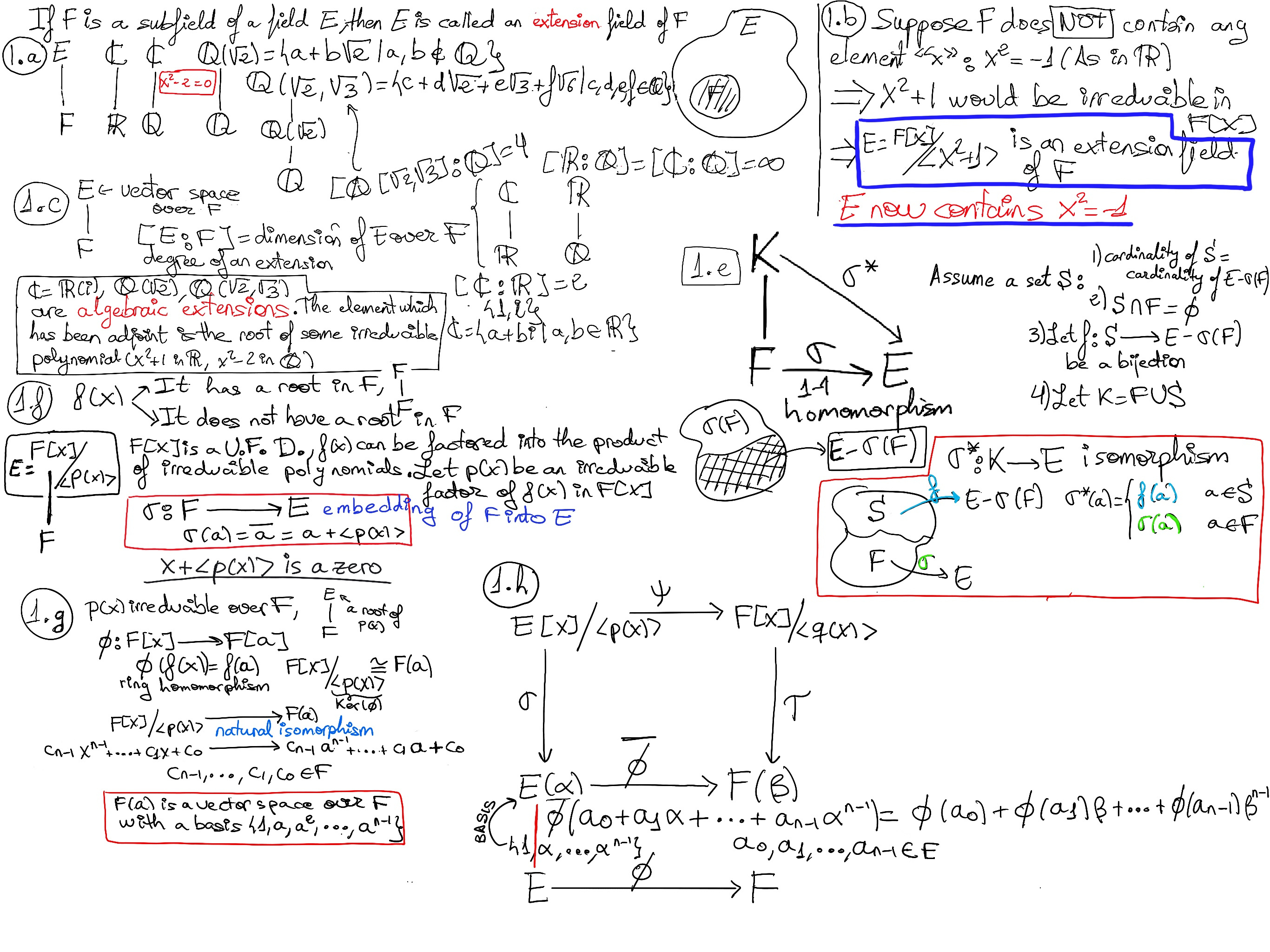
A basis for a n-dimensional vector space over a field F is a set of n vectors, {v1, v2, ···, vn} such that every member of the vector space can be expressed or written as a linear combination of the basis vectors in a unique way, i.e.,uniquely in the form a1v1 + a2v2 + ··· anvn. Therefore, the theorem says that if a is a root of an irreducible polynomial over F of degree n, then the set {1, a, ···, an-1} is a basis for F(a) over F.
Proof.
Let Φ: F[x] → F(a), Φ(f(x)) = f(a), Φ is obviously a ring homomorphism.
We claim that Ker(Φ) = ⟨p(x)⟩.
We have an isomorphism F[x]/⟨p(x)⟩ with its image under Φ, contained in F(a), i.e. F[x]/Ker(Φ) = F[x]/⟨p(x)⟩ ≋ Φ(F[x]) = F(a).
F[x]/⟨p(x)⟩ is a field ⇒ Φ(F[x]) is a field, too -besides that we know that Φ(F[x]) is a subfield of F(a)-. It contains both F and a, and therefore contains the smallest subfield that contains both F and a, that is, F(a), hence Φ(F[x]) = F(a).
Notice that every element of F[x]/⟨p(x)⟩ can be expressed uniquely in the form cn-1xn-1 + cn-2xn-2 + ··· + c1a + c0 + ⟨p(x)⟩ where c0, c1, ···, cn-1 ∈ F and the natural isomorphism from F[x]/⟨p(x)⟩ to F(a) carries ckxk + ⟨p(x)⟩ to ckak ⇒ every member of F(a) can be uniquely expressed in the form cn-1an-1 + cn-2an-2 + ··· + c1a + c0, where c0, c1, ···, cn-1 ∈ F∎
Degree of Splitting Field. For any field F and any polynomial p ∈ F[x] of degree n, there exists a splitting field K/F for p, and [K : F] ≤ n!
Proof.
We are going to use induction on n = deg(p(x)).
Base case, n = 1 ⇒ p(x) = ax + b = a(x + b·a-1) ⇒ There is a single root, namely -b·a-1 ∈ F. Therefore, K = F is a splitting field of p, [F : F] = 1 ≤ 1!
Inductive step. Suppose that any polynomial of degree n -1 over any field has a splitting field extension of degree at most (n-1)!, and let p ∈ F[x], deg(p) = n. Obviously, we are going to use strong induction.
Choose any irreducible factor q ∈ F[x] of p of degree k ≤ n, and define the field K = F[x]/⟨q(x)⟩. Then, [K : F] = k. Besides, we denote the element x + ⟨q(x)⟩ by α, then q(α) = 0🔑 (x -α is a linear factor of q), so since q divides p, we could write p = (x -α)·p1(x) for a polynomial p1(x)∈ K[x] of degree n-1.
🔑 F field, q ∈ F[x] irreducible, K = F[x]/⟨q(x)⟩. Then, K is a simple algebraic extension F[α] of F, and α = x + ⟨q(x)⟩ has minimum polynomial q over F. Hint: for each polynomial f = a0 + a1x + a2x2 + ··· anxn ∈ F[x], f(α) = a0 + a1α + a2α2 + ··· anαn = a0 + a1(x + ⟨q(x)⟩) + a2(x + ⟨q(x)⟩)2 + ··· an(x + ⟨q(x)⟩)n = a0 + a1(x + ⟨q(x)⟩) + a2(x2 + ⟨q(x)⟩) + ··· an(xn + ⟨q(x)⟩) = a0 + a1x + a2x2 + ··· anxn + ⟨q(x)⟩ = f + ⟨q(x)⟩ ⇒ Therefore, ∀f ∈ F[x], f(α) = f + ⟨q(x)⟩. If f(α) = 0 (i.e., α is a root of f) ↭f ∈ ⟨q(x)⟩ ↭ q(x)|f. Therefore, q(x) is the irreducible polynomial of α - the polynomial of lowest degree having coefficients in the field, such that α is a root of the polynomial-, and in particular, q(α) = 0.
By the induction hypothesis, there exists a splitting field for p1(x) over K, say L, of degree at most (n-1)! ⇒ [L : F] = [L : K]·[K : F]≤ (n-1)!·k ≤ (n-1)!·n = n!, and p(x) splits completely in L, say as p(x) = c(x -α)(x - r1)(x -r2)···(x -rn-1). The subfield F(α, r1,···, rn-1) of L is a splitting field for p, and its degree is at most n!∎
Corollary. Let F be a field and let p(x) ∈ F[x] be irreducible over F. If a is a zero of p(x) in some extension E of F and b is a zero of p(x) in some other extension E' of F, then both fields F(a) and F(b) are isomorphic.
Proof.
Recall, theorem. Let F be a field and let p(x) ∈ F[x] be an irreducible polynomial over F, deg(p(x)) = n. If a is a root of p(x) in some extension E of F, then F(a) ≋ F[x]/⟨p(x)⟩.
😃 A simple line proof, F(a) ≋ F[x]/⟨p(x)⟩ ≋ F(b)
Example. f(x) = x6 -2 over ℚ. We know that $\sqrt[6]{2}$ is a zero of f(x), and therefore the set {1, $\sqrt[6]{2}, \sqrt[6]{2^2}, \sqrt[6]{2^3}, \sqrt[6]{2^4}, \sqrt[6]{2^5}$} is a basis for ℚ($\sqrt[6]{2}$) over ℚ. ℚ($\sqrt[6]{2}$) = {$a_0 + a_1\sqrt[6]{2} + a_2\sqrt[6]{2^2}, + a_3\sqrt[6]{2^3} + a_4\sqrt[6]{2^4} + a_5\sqrt[6]{2^5}$| ai ∈ ℚ} ≋ ℚ[x]/⟨x6 -2⟩.
Observe that any ring isomorphism Φ from F to F’ has a natural extension from F[x] to F’[x], we will use Φ to denote this mapping, too, given by Φ(cnxn + cn-1xn-1 + ··· + c1x + c0) = Φ(cn)xn + Φ(cn-1)xn-1 + ··· + Φ(c1)x + Φ(c0).