Relations

The Cartesian product of two sets A and B, denoted A x B, is the set of all possible ordered pairs (a, b), where the first element of each pair, a, is an element of A, and the second, b, is an element of B. We could express this in a more mathematical or formal language as A x B = {(a, b): a ∈ A and b ∈ B}, e.g., {1, 2} x {red, yellow, blue} = {(1, red), (1, yellow), (1, blue), (2, red), (2, yellow), (2, blue)}

We define the Cartesian product of n sets to be, $\prod_{i=1}^n A_i=A_1x···xA_n=$ {(a₁,···,a_n) | a_i ∈ A for i = 1,···n}, we often write Aⁿ for A x ··· (n times) x A, e.g., A = {a, b, c}, B = {0, 1}, A x B = {(a, 0), (a, 1), (b, 0), (b, 1), (c, 0), (c, 1)}, A x ∅ = ∅ x A = ∅, |A x B| = |A|·|B| = 3·2 = 6.

It is written in latex as \prod_{i=1}^n A_i.

Fact: A x B ≠ B x A, that is, the order really matters, e.g., (b, 0) ∈ A x B, but (b, 0)∉ B x A because b ∉ B.

Definition. A relation R on a set S is a subset of S x S, that is, a set of ordered pairs.If (a, b) ∈ R, we express it or write it as a R b or a ~ b.

Thus, a relation between the sets A and B is a subset of their Cartesian product A x B, i.e., R ⊆ A x B. For any two arbitrary elements a ∈ A and b ∈ B, we say that a is related to b with respect to R, denoted as a R b or a ~ b, if and only if (a, b) ∈ R.

Examples:

• Country/Capital: {(USA, Washington), (China, Beijing), (France, Paris), (Spain, Madrid), …}
• A = {1, 2, 3}, R is less than or equal. 1 ≤ 1, 1 ≤ 2, 1 ≤ 3, 2 ≤ 2, 2 ≤ 3, 3 ≤ 3. R = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 3)}.
• {(x, y) ∈ ℕ²: x = y}, 1 ~ 1, 2 ~ 2, 3 ~ 3.
• {(x, y) ∈ ℕ²: x > y}, 2 ~ 1, 3 ~ 2, 3 ~ 1.
• {(x, y) ∈ ℕ²: x ≥ y}, 2 ~ 1, 2 ~ 2, 3 ~ 2, 3 ~ 1.
• {(m, n) ∈ ℝ²: m divides n} = {(m, n) ∈ ℝ²: ∃d ∈ ℕ n = md}. 2 ~ 6, 3 ~ 6, 7 ~ 56.

Typically, in these last examples, we write m > n, m ≥ n and m|n instead of m R n or m ~ n if (m, n) ∈ R.

Let S be any set and let R be equality, x R y or (x, y) ∈ R ↭ x = y. R = {(a, a)| a ∈ A}. Example. S = {1, 2, 3}, R = {(1, 1), (2, 2), (3, 3)}

Properties of relations

Given a set S, a relation R on S, and x, y, z ∈ S.

1. R is reflexive if each element of the set S is related or linked to itself, i.e., x R x ∀x ∈ S (for every x in S). Otherwise, R is said to be non-reflexive. The relations =, | and ≤ are reflexive.
   Let S = {a, b}, R = {(a, a), (a, b)}. S is neither reflexive, nor anti-reflexive. R is called irreflexive or anti-reflexive if not x ~ x ∀x ∈ S.
2. R is symmetric if when a first element is related to a second then the reverse is also true, that is, the second element is related to the first, i.e. x R y ⇒ y R x; otherwise, R is non-symmetric. Equality is symmetric, but ≤ is not (3 ≤ 4 but 4 ≤ 3 is False)
3. R is antisymmetric if two distinct elements are never related in both directions. In other words, whenever x R y and y R x then x = y. The “less than” relation < is antisymmetric because if a < b, b is not less than a, so the premise of the definition is never satisfied. ≤ is also antisymmetric, a ≤ b, b ≤ a ⇒ a = b. The divides relation in a set of positive integer is anti-symmetric, too.
4. R is transitive if when a first element is related to a second which, in turn, is related to a third, then the first element is related to the third element, i.e., x R y and y R z ⇒ x R z; otherwise, R is nontransitive. The relations =, <, and ≤ are all transitive.

A relation is a partial order when it is reflexive, antisymmetric, and transitive. For example, (ℝ, ≤) and (ℕ, divisibility) = {(m, n) ∈ ℕ²: m divides n} are good examples: Reflexive (a|a ∀a∈ ℕ), Antisymmetric (if a|b and b|a then a = b), and Transitive (a|b and b|c, then a|c). The set of subsets of a given set (its power set, say P(S)) ordered by inclusion is another example.

A partial order relation that provides a way to compare between any two elements of a set is called a total order relation, that is, ∀ x, y ∈ S, either x R y or y R x (or both). For example, the set of integers over the relation “less than or equal to” is a totally ordered set because for every element a and b in the set of integers, either a ≼ b or b ≼ a.

Equivalence relations

In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. It is generally represented by the symbol “∼”.

Examples.

• Let A be any set. There are two trivial equivalence relations: equality (a, b) ∈ R ↭ a = b and R = {(a, b) ∈ R, ∀a, b ∈ A} = A x A.
• Let n ∈ ℤ, n ≥ 2, {(a, b) ∈ ℤⁿ: n divides (a-b)} = {(a, b) ∈ ℤⁿ: n | (a-b)} is an equivalence relation, you may often see it as a ∼ b and expressed as “a = b mod n”.

Proof.

Reflexive property. a R a because n (n ≥ 2) divides 0.
Symmetric property. a R b ⇨ ∃k ∈ Z: a - b = kn ⇨ b - a = -kn, and therefore, b R a.
Transitive property. a R b and b R c ⇨ ∃k,l ∈ ℤ: a - b = kn, b - c = ln ⇨ a - c = (a - b) + (b - c) = (k+l)n, and therefore, a R c.

• “is equal to” is an equivalent relation on ℝ as ∀a, b, c ∈ ℝ, ⇨ Reflexive property (a = a), Symmetric property (a = b ⇒ b = a), and Transitive property (a = b, b = c ⇒ a = c).

• ‘Has the same absolute value’ is an equivalence relation on ℂ. More formally, S = ℂ, with z ∼ w ⇔ |z| = |w|.

Proof:

∀a, b, c ∈ ℂ, Reflexivity property (|a| = |a|), Symmetric property (|a| = |b| ⇒ |b| = |a|), and Transitive property (|a| = |b| and |b| = |c| ⇒ |a| = |c|).

• Let S = M_n(ℝ), the set of n × n matrices with real coefficients. We define ∼ on M_n(ℝ) by saying A ∼ B if and only if there exists an invertible matrix P such that A = P^-1BP. A and B are said to be similar. In other words, matrix similarity is an equivalence relation.

  In linear algebra, an n-by-n square matrix is called invertible if the product of the matrix and its inverse is the identity matrix, that is, AA^-1=I_n. If A and B are two invertible matrices of the same order then (AB)^-1 = B^-1A^-1.

Proof:

∀A, B, C ∈ M_n(ℝ),
Reflexive property: A = I^-1AI, I is the identity matrix, that is, a square matrix having 1s on the main diagonal, and 0s everywhere else.
Symmetric property: A = P^-1BP ⇒ B = PAP^-1 = (P^-1)^-1AP^-1, i.e., B ∼ A for P^-1.
Transitive Property: A = P^-1BP and B = Q^-1CQ for some P, Q ⇒ A = P^-1Q^-1CQP = [If P and Q are invertible matrices of the same order, then (PQ)^-1 = Q^-1P^-1] (QP)^-1C(QP).

• Let S be the set of all triangles in a plane, a, b ∈ S, a ∼ b if a and b are similar. Then, ∼ is an equivalence relation on S.

  Two triangles are similar if their corresponding angles are equal. This implies that they are similar if and only if the corresponding sides are proportional.

• We could define an equivalence relation on the set of all ordered pairs of natural numbers (a, b), a, b ∈ ℕ as follows: (a, b) ~ (c, d) ↭ a + d = c + b. The set of integers is the set of all equivalence classes of such ordered pairs. ℤ = {[a, b]: (a, b) ∈ ℕ²}

We can define integer addition and multiplication as two maps +: ℤ x ℤ → ℤ, ·: ℤ x ℤ → ℤ,: [(a, b)] + [(c, d)] = [(a + c, b + d)], [(a, b)] · [(c, d)] = [(ac + bd, ad + bc)]

• Let S = {(a, b) | a, b ∈ ℤ, b ≠ 0}, (a, b), (c, d) ∈ S, (a, b) ∼ (c, d) if their fractions are equal, i.e., ^a⁄_b = ^c⁄_d, that is ad = bc. Then, ∼ is an equivalence relation.

Proof:

Reflexivity (a, b) ∼ (a, b) because ab = [Commutativity of multiplication] ba.
Symmetric (a, b) ∼ (c, d) ⇒ ad = bc ⇒ [Commutativity of multiplication] cb = da ⇒ (c, d) ∼ (a, b).
Transitivity (a, b) ∼ (c, d) and (c, d) ∼ (e, f) ⇒ ad = bc and cf = de ⇒ adf = bcf = bde ⇒ [∴ Commutativity of multiplication] afd = bed ⇒ [∴ We can cancel d because d ≠ 0] af = be ⇒ (a, b) ∼ (e, f)

S = {(a, b) | a, b ∈ ℤ, b ≠ 0}, (a, b), (c, d) ∈ S, (a, b) ∼ (c, d) ↭ ad = bc. ℚ = {[a, b] | a, b ∈ ℤ, b ≠ 0}, so the rational is the set of equivalence classes of ordered pairs of integers. Irreducible fractions (the numerator and denominator are integers that have no other common divisor than 1) are typically chosen for the representatives of these equivalence classes.

• A = {f | f: ℝ → ℝ and f is differentiable}, f R g ↭ f’ = g’.
• Counterexamples: (ℝ, >) is neither reflexive, nor symmetric, (ℝ, ≥) and (ℝ, ≤) are not symmetric, e.g., 2 ≥ 1 but 1 $\not\geq$ 2. Let S denote the set of people, S = {humans}, and ~ be the relation defined as x ~ y ↭ x is the brother of y. It is not reflexive (no person can be his or her own brother). If x ~ y (John -x- is the brother of Eva -y-) ⇒ it is not necessarily the case that -y- Eva is the brother of John -x- because Eva is a girl/woman. {humans}, x ~ y ↭ x loves y is neither reflexive (Some people do not love themselves), symmetric, nor transitive.

Equivalence Class

Definition. An equivalence class is a subset of S which includes all elements that are related or equivalent to each other by some equivalence relation. More formally, give an equivalent relation ∼ on S, and an element x ∈ S, the equivalence class of x, typically denoted by x or [x] is the subset x = {y ∈ S : y ∼ x}, and each element of the set is called a representative of the equivalence class.

Examples:

• Suppose that S is the set of all children playing in a garden. Then, if ~ is the equivalent relation ‘of the same age’ children, one equivalence class would be the set of all 7-year-olds, and another the set of all 5-year-olds.

• Let A be any set and let be R the equality =. ∀a ∈ A, [a] = {b ∈ A | a = b} = {a}

• Suppose that S is the set of all polygons. Then, if ~ is the equivalent relation defined as polygons with the same number of sides. Then, a few examples of equivalences classes would be the set of all triangles, the set of all quadrilaterals, the set of all pentagons, and so on.

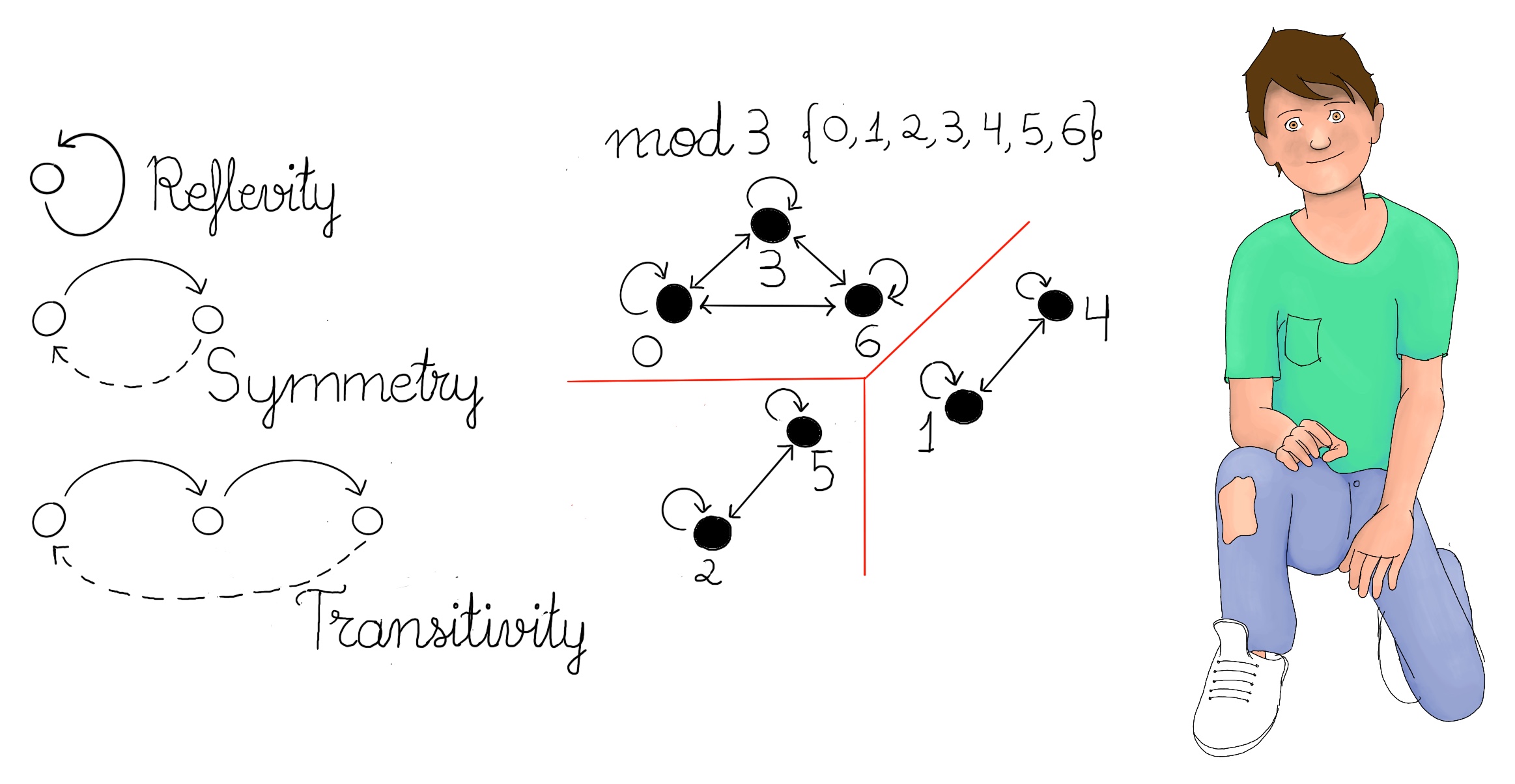
• If ~ is the equivalent relation “congruence module n”, n ∈ ℤ, n ≥ 2, {(a, b) ∈ ℤ²: n divides (a-b)}, the equivalence class of 1, 1 = {. . . , −n + 1, 1, n + 1, 2n + 1, . . .}; 2 = {. . . , −n + 2, 2, n + 2, 2n + 2, . . .};  

• Let S be the set of all polynomials with real coefficients. If f, g ∈ S, let’s define f ~ g ↭ f’ = g’. Then, ~ is an equivalence relation on S. f = [f] = {g ∈ S : f’ = g’} = {g ∈ S : (f - g)’ = 0} = {f + c | c ∈ ℝ}.

Partitions

A partition of a set S is a grouping of its elements into non-empty subsets A_i ≠ ∅, in such a way that every element is included in exactly one subset. In other words, it is a collection of non-empty subsets or parts A_i which are exhaustive (whose union is the entire set) and mutually exclusive (they are disjoint subsets). More formally, {A_i ⊆ S : i ∈ I} where I is an indexing set, with satisfies,

1. A_i ≠ ∅, ∀i ∈ I, that is, all the subsets are non-empty. The subsets are the cells of the partition.
2. ∪_i∈I A_i = S, that is, every member of S lies in one of the subsets. They are exhaustive, i.e., their union is the entire set.
3. A_i ∩ A_j = ∅ ∀i,j∈ I, i≠j, that is, they are disjoint subsets (they do no overlap). Figure 1.a.  

Examples.

• {1, 2} and {3} forms a partition of the set {1, 2, 3}. {1, 2}, {3, 5, 7}, {4, 6} forms a partition of the set {1, 2, 3, 4, 5, 6, 7}. Finally, {A, E, I, O, U}, {B, C, D, F, G, J, K, L, M, N, P, Q, S, T, V, X, Z} and {H, R, W, Y} forms a partition of the English alphabet.
• The set of naturals can be partitioned into two sets based on parity. {n ∈ ℕ : n is divisible by 2} and {n ∈ ℕ : n + 1 is divisible by 2} form a partition of ℕ into odds and evens.
• Congruence mod n partitions ℤ into n equivalence classes or partitions. These cells are the residue classes modulo n in ℤ, e.g., congruence mod 3 partitions the integers into 3 equivalence clases: {0, ±3, ±6, ±9, ±12…}, {1±3, 1±6, 1 ±9, ±12…}, and {2±3, 2±6, 2±9, ±12…}.
• The set of integers can be partitioned into three disjoint sets, Z = −ℕ ∪ {0} ∪ ℕ, where ℕ = {1, 2, 3,… } = Natural Numbers = Positive Integers.

Equivalence Classes and Partitions

For any equivalence relation ∼ on a set S, the equivalence classes of the equivalence relation on a set S form or constitute a partition of S. Conversely, for any partition P of S, there is an equivalence relation on S by relating elements if they lie in the same part or subset of the partition.

Basically, we can define an equivalence relation on S by saying x ~ y if and only if x and y are elements in the same part or subset of the partition P. Thus, the notions of equivalence relation and partition are essentially the same thing.

Proof:

Suppose that ∼ is an equivalent relation on S. If x∈S, let $\bar{x}$ = S(x) = {y ∈ X | y ∼ x}. Thus, S(x) is the equivalence class of x. By the reflexive property, x ∼ x, so x ∈ S(x) ⇨ S = ∪_x∈XS(x). However, some of the S(x)’s may be identical, so let’s get rid of the duplicates.

In other words, we have S = ∪_x∈YS(x) and Y is a subset of S. If x, y∈Y and x≠y, then by construction, S(x)≠S(y). ¿Do they intersect?

For the sake of contradiction, suppose x, y∈Y, x≠y, but z∈ S(x)∩S(y). z∈ S(x) ⇨ z ∼ x, and z∈ S(y) ⇨ z ∼ y. x ∼ z (by symmetry) and z ∼ y ⇨ x ∼ y (by transitivity).

Let’s see that S(x)=S(y). First, let’s prove that S(x) ⊆ S(y). Suppose w ∈ S(x) ⇒ w ∼ x, but we already know that x ∼ y ⇨ w ∼ y (by transitivity) ⇨ w ∈ S(y). Secondly, let’s prove that S(y) ⊆ S(x). Suppose w ∈ S(y), w ∼ y, y ∼ x (by symmetry) ⇨ w ∼ x (by transitivity) ⇨ w ∈ S(x), and by double inclusion, S(x)=S(y) ⊥ that is a contradiction because we threw out all the duplicates earlier.

Conversely, suppose {X_i}_i∈I is a partition of S. Let’s define a relation on S by saying x ∼ y if and only if x, y∈X_i for some i∈I.

1. Reflexive. If x∈S ⇨ x ∈X_i for some i∈I (every member of S lies in one of the subsets -Partition’s definition ii-). Obviously, x is in the same X_i than itself ⇨ x, x ∈X_i so x ∼ x.
2. If x ∼ y, then x, y ∈X_i for some i∈I, and obviously y, x ∈X_i, so y ∼ x.
3. If x ∼ y and y ∼ z, then x, y∈X_i and y, z ∈X_j ⇨ y ∈ X_i∩X_j, but the partition’s subsets are disjoint (Partition’s definition iii) ⇨ X_i = X_j ⇨ x, y, z ∈ X_i and in particular, x, z ∈ X_i ⇨ x ∼ z.

An important example

Let r ∈ ℤ, r ≥ 1. We know that n∼m iff r |(n-m) is a equivalent relation. We call $\frac{ℤ}{rℤ}$ = { equivalent classes [n] for r}, and define addition on $\frac{ℤ}{rℤ}$ by [n] + [m] = [n+m]. This operation is well-defined and $\frac{ℤ}{rℤ}$ is an Abelian group with this operation.