Irreducibility Tests

Doctors are semi-gods beings, completely infallible, only do good, and money does not corrupt medicine, so turn off this monkey brain of yours and outsource all of your thinking to them -you are welcome! Apocalypse, Anawim, #justtothepoint.

Recall

Definition. Let D be an integral domain. An irreducible polynomial is, roughly speaking, a polynomial that cannot be factored into the product of two non-constant polynomials. A non-zero and non-unit polynomial f(x) ∈ D[x] is said to be irreducible if it cannot be written or expressed as the product of two non-units. In other words, whenever f(x) is expressed as a product of two polynomials g(x)h(x) with g(x) and h(x) ∈ D[x], then either g(x) or h(x) is a unit in D[x].

A non-constant polynomial f(x) ∈ F[x], F field, is said to be irreducible if f(x) cannot be expressed a as a product of two polynomials g(x), h(x) ∈ F[x] of lower degree, that is, f(x) = g(x)h(x), deg(g(x)) < deg(f(x)) and deg(h(x)) < deg(f(x)).

Reducibility test for polynomials with degrees two or three. Let F be a field. If f(x) ∈ F[x] and deg(f(x)) = 2 or 3, then f(x) is reducible over F iff f has a zero in F or f(x) is irreducible over F iff f(α) ≠ 0 ∀α ∈ F.  

Theorem. Let f(x) ∈ ℤ[x]. If f(x) is reducible over ℚ, then it is reducible over ℤ.

Proof.

Suppose f is reducible over ℚ ⇒ ∃g(x), h(x) ∈ ℚ[x] such that f(x) = g(x)h(x) with both polynomials g(x) and h(x) having degree less than of f(x). We could assume that f is primitive because we can divide both f and g by the content of f.

Next, let a and b be the least common multiple of the denominators of the coefficients of g and h respectively, so abf(x) = ag(x)·bh(x), where ag(x) ∈ ℤ[x] and bh ∈ ℤ[x].

Now, let c and d be the content of ag(x) and bh(x) respectively ⇒ ag(x) = cg’(x) and bh(x) = dh’(x) where both g’(x) and h’(x) are primitives ⇒ abf(x) = (ag(x))·(bh(x)) = (cg’(x))(dh’(x)) = cdg’(x)h’(x), where both g’(x) and h’(x) are primitives polynomials in ℤ[x], so their product is primitive, and f is primitive, too ⇒ content(abf(x)) =[f is primitive] ab = content(cdg’(x)h’(x)) =[g’(h)h’(x) is primitive] cd ⇒[ab = cd & abf(x) = cdg’(x)h’(x) & Cancellation law applies] f(x) = g’(x)h’(x) where both g’(x) and h’(x) are primitives polynomials in ℤ[x] and deg(g’(x)) = deg(g(x)) and deg(h’(x)) = deg(h(x)) and both polynomials g’ and h’ having degrees less than of f, therefore f is reducible over ℤ ∎

Mod p Irreducibility Test. Let p be a prime, f(x) ∈ ℤ[x], and deg(f(x)) ≥ 1. Let f'(x) be the polynomial in ℤ_p[x] obtained from f(x) by reducing all the coefficients of f(x) modulo p. If f'(x) is irreducible over ℤ_p and deg(f'(x)) = deg(f(x)), then f(x) is irreducible over ℚ.

Proof.

Suppose f’(x) is irreducible over ℤ_p and deg(f’(x)) = deg(f(x)). For the sake of contradiction, let us assume f is reducible over ℚ ⇒[Theorem. Let f(x) ∈ ℤ[x], then f(x) is irreducible over ℚ, then it is reducible over ℤ.] f is reducible over ℤ, that is, ∃g(x), h(x) ∈ ℤ[x], f(x) = g(x)h(x) with both polynomials g(x) and h(x) having degree less than of f(x) ⇒[f is reducible] 1 ≤ deg(g)< deg(f) and 1 ≤ deg(h) < deg(f). Then, the idea is that the same relationship holds taking all coefficients modulo p.

Let f’, g’, and h’ be the polynomials obtained from f, g, and h by reducing all the coefficients modulo p.

Since deg(f) = deg(f’) ⇒ deg(g’) ≤ deg(g) < deg(f’) and deg(h’) ≤ deg(h) < deg(f’) and f’ = g’h’ ⇒ f’ = g’h’, deg(g’) < deg(f’) and deg(h’) < deg(f’) ⊥ Therefore, this contradicts our assumption that f’(x) is irreducible over ℤ_p, so f is irreducible over ℚ.

In fact, deg(g’) = deg(g) and deg(h’) = deg(h). Otherwise, deg(f’) = deg(g’h’) = deg(g’) + deg(h’) < deg(g) + deg(h) = deg(gh) = deg(f) ⊥ By assumption, deg(f) = deg(f’).

Examples.

• f(x) = x³ + x +1 ∈ ℤ[x], x³ + x +1 ∈ ℤ/2ℤ[x], 1³ +1 +1 = 3 = 1, 0³+0 +1 =1, deg(f) = 3 ⇒ It is irreducible over ℤ/2ℤ ⇒ It is irreducible over ℚ.
• f(x) = x⁵ +9x⁴ +12x² +6. f’(x) = x⁵ + x⁴ = x⁴(x + 1) over ℤ₂, f’ is reducible over ℤ₂, so we cannot apply Mod p = 2 Irreducible Test. f’(x) = x⁵ = x³·x² over ℤ₃, f’ is reducible over ℤ₃, so we cannot apply Mod p = 3 Irreducible Test. f’(x) = x⁵ +4x⁴ + 2x² + 1 over ℤ₅. Let’s evaluate f’(0) = 1 ≠ 0, f’(1) = 3 ≠ 0, f’(2) = 10 = 0 ⇒ f’(x) = (x-2) g(x) so f’ is reducible over ℤ₅, so we cannot apply Mod p = 5 Irreducible Test.
• f(x) = x³ + 7x + 16. f’(x) = x³ + 2x +1 over ℤ₅. Since it has degree 3 and has no root in ℤ₅[x], it is irreducible in ℤ₅[x] ⇒ f(x) is irreducible in ℚ[x].
• f(x) = 21x³ -3x² +2x +9. f’(x) = x³ +x² +1 over ℤ₂. Since it has degree 3 and has no root in ℤ₂[x] (f’(0) = f’(1) = 1), it is irreducible in ℤ₂[x] ⇒ f(x) is irreducible in ℚ[x]. However, f’(x) = 2x over ℤ₃, f' is irreducible but 💀 we cannot apply p = 3 Irreducible Test because deg(f(x)) ≠ deg(f'(x)).
• f(x)=(3/7)x⁴ -(2/7)x² + (9/35)x + 3/5. Let h(x) = 35f(x) = 15x⁴ -10x² + 9x +21. h’(x) = x⁴ +x +1 in ℤ₂[x]. It is irreducible over ℤ₂[x] because it has no zeros in ℤ₂[x] and has no quadratic factor either (There are two options: a) x² + x + 1 is not a factor; b) and x² + 1 has a zero in x=1, but h’ does not, so it is not possible h’ = (x² + 1)·h’’) ⇒ h(x) is irreducible over ℚ ⇒ f(x) is irreducible over ℚ. (Figure 1.a.)  

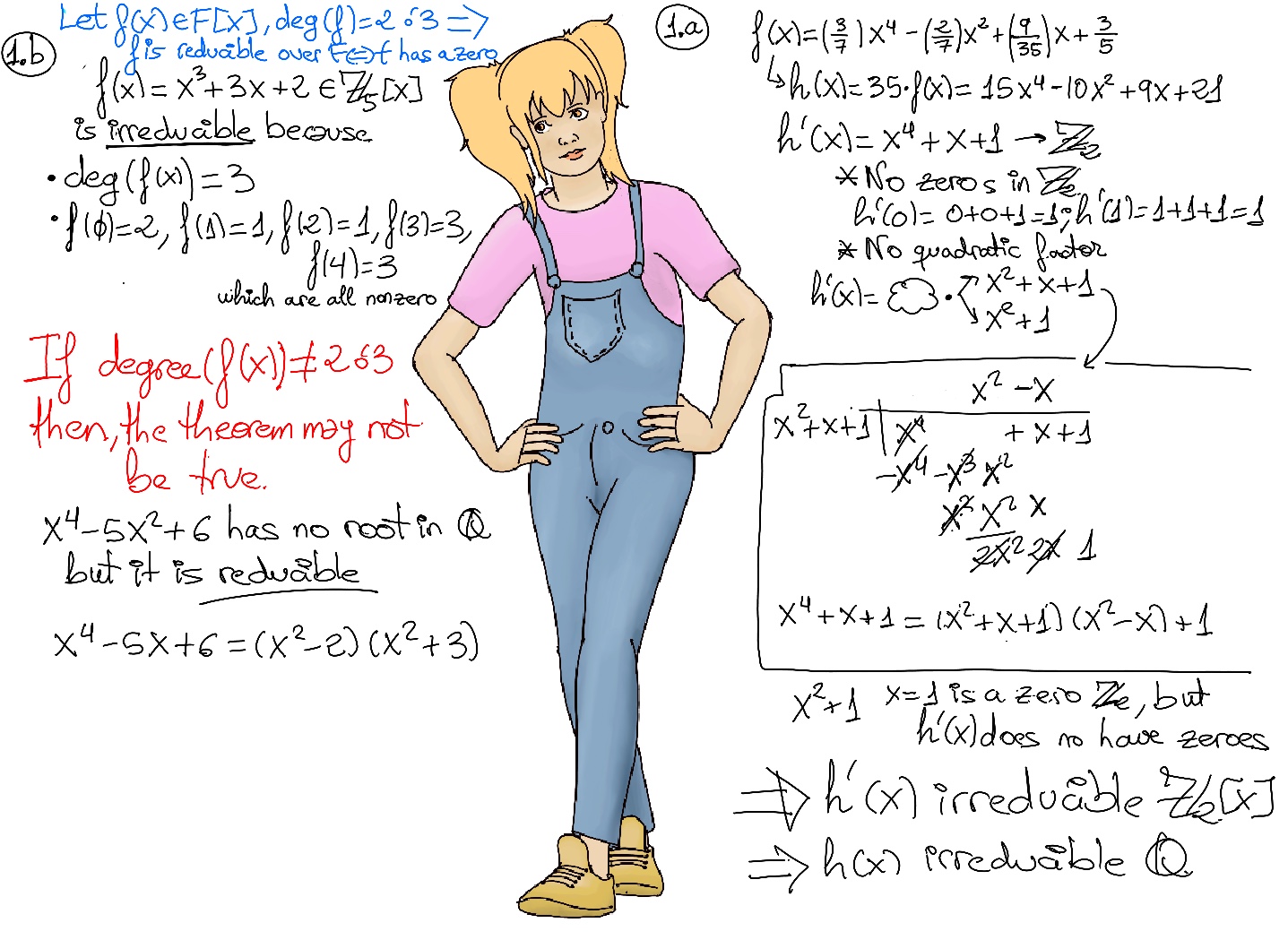
Eisenstein Criterion. Let p ∈ ℤ be a prime. If f(x) = a_nxⁿ + a_n-1x^n-1 + ··· + a₀ in ℤ[x] have degree ≥ 1 with

1. p divides all the coefficient, except the leading one, that is, p | a₀, p | a₁, ···, p | a_n-1
2. p does not divide the leading term, p ɫ a_n
3. p² ɫ a₀

Then, f(x) is irreducible in ℚ[x].

Proof:

This proof is by contradiction. Let’s assume that f is not irreducible. If f(x) is reducible over ℚ ⇒[Theorem. Let f(x) ∈ ℤ[x], then f(x) is irreducible over ℚ, then it is reducible over ℤ.] f is reducible over ℤ, that is, ∃g(x), h(x) ∈ ℤ[x]: f(x) = g(x)h(x) and the degrees of g and h are less than n.

Say g(x) = b_rx^r + ··· + b₀, h(x) = c_sx^s + ··· + c₀.

Since p | a₀, p² ɫ a₀, and a₀ = b₀c₀ ⇒ p divides b₀ or c₀, but not both. Let’s suppose p | b₀ and p ɫ c₀ without any loss of generality.

Since p ɫ a_n = b_rc_s ⇒ p ɫ b_r, but p | b₀, hence there is a least integer t such that p ɫ b_t (p | b_t-1, ··· p | b₁, p| b₀). Next, let us consider a_t = b_tc₀ + b_t-1c₁ + ··· + b₀c_t. Then, p | a_t (Notice that r = deg(g(x)) = deg(b_rx^r + ··· + b₀) < n ⇒ t ≤ r < n ), and p divides every summand on the right after the first term b_tc₀, that is, (b_t-1c₁ + ··· + b₀c_t) ⇒ p | b_tc₀, p prime ⊥ p ɫ b_t, p ɫ c₀

Examples

• f(x) = x⁵ +9x⁴ + 12x² +6, 3 ɫ 1, 3 | 9, 3 | 12, 3 | 6, 3² = 9 ɫ 6, then f(x) is irreducible over ℚ.
• f(x) = x⁴ + 3x² + 3, 3 ɫ 1, 3 | 3, 3 | 3, 3² ɫ 3, then f(x) is irreducible over ℚ.
• f(x) = 5x¹⁰ -3x⁷ -6x³ +15x² -9x +6 ∈ ℤ[x], then f(x) is irreducible over ℚ (p = 3).
• xⁿ-2 ∈ ℤ[x], n ≥ 2 is irreducible over ℚ (Eisenstein criteria, p=2) ∀n ≥ 2, so there are irreducible polynomials over ℚ of arbitrary high degree. This is not true over ℝ. We know that any irreducible polynomial over ℝ has degree 1 or 2.
• f(x) = x⁵ +3x³ -3x +6, 3 ɫ 1, 3 | 3, 3 | -3, 3 | 6, 3² = 9 ɫ 6, then f is irreducible over Q.
• f(x) = x² +x +2 ∈ ℤ[x]. By changing x → x + 3, f’(x) = x² + 6x + 9 + x + 3 + 2 = x² + 7x + 14 is irreducible over ℚ (Eisenstein p = 7)

  Eisenstein theorem applies after substitution x → x + a. If the polynomial after substitution (is is just an automorphism of the ring ℚ([x]), and automorphisms preserve algebraic properties) is irreducible then allows concluding that the original polynomial is irreducible as well.

Corollary. For any prime p, the pth cyclotomic polynomial Φ_p(x) = $\frac{x^p-1}{x-1}=x^{p-1}+x^{p-2}+···+x+1$ is irreducible over ℚ.

Proof. Let f(x) = Φ_p(x+1) = $\frac{(x+1)^p-1}{(x+1)-1}=x^{p-1}+(\begin{smallmatrix}p\\ 1\end{smallmatrix})x^{p-2}+(\begin{smallmatrix}p\\ 2\end{smallmatrix})x^{p-3}+···+(\begin{smallmatrix}p\\ p-2\end{smallmatrix})x+(\begin{smallmatrix}p\\ p-1\end{smallmatrix})1$

f(x) does satisfy the conditions of Eisenstein’s criterion because $(\begin{smallmatrix}p\\ k\end{smallmatrix})$ is divisible by p for 1 ≤ k ≤ p−1, p ɫ 1, and $(\begin{smallmatrix}p\\ p-1\end{smallmatrix})$ is not divisible by p² ⇒ Φ_p(x+1) is irreducible.

But if Φ_p(x) = g(x)h(x) were a nontrivial factorization of Φ_p(x) over ℚ, then so would Φ_p(x+1) be no trivially factored, Φ_p(x+1) = g(x+1)h(x+1) ⊥

Examples: p = 2, $\frac{x^2-1}{x-1}=x+1$ is irreducible over ℚ. p = 3, $\frac{x^3-1}{x-1}=$ x² + x + 1 is irreducible over ℚ.

Rational root test. Let f = a_nxⁿ +a_n-1x^n-1 + ··· + a₀ ∈ ℤ[x], a₀a_n ≠ 0. Each rational solution r/s written in lowest terms so that r and s are relatively prime, satisfies that r is a factor of the constant term a₀ (r | a₀) and s is a factor of the leading coefficient a_n (s | a_n).

Proof.

Let f = a_nxⁿ +a_n-1x^n-1 + ··· + a₀ ∈ ℤ[x], let r/s be a rational solution.

a_n^rn⁄_sⁿ + ··· + a₁^r⁄_s + a₀ = 0 ⇒ [Multiply by sⁿ] a_nrⁿ + a_n-1r^n-1s + ··· + a₁rs^n-1 + a₀sⁿ = 0 ⇒ r(a_nr^n-1 + ··· + a₁s^n-1) = -a₀sⁿ ⇒ r | a₀sⁿ ⇒ [r and s are coprime] r | a₀.

Similarly, a_nrⁿ + a_n-1r^n-1s + ··· + a₁rs^n-1 + a₀sⁿ = 0 ⇒ s(a_n-1r^n-1 + ··· + a₁rs^n-2 +a₀s^n-1) = -a_nrⁿ ⇒ s | a_nrⁿ ⇒ [r and s are coprime] s | a_n∎

Examples

• x³-x-1, x³-3x +1 are irreducibles because any root r/s must have r = ±1, s = ±1, but they are not roots.
• 3x³-11x²+5x-3. Possible roots can be ±1, ±3, ±¹⁄₃. The actual rational roots of the function are 1, 3, and ^-1⁄₃. 3x³-11x²+5x-3 = (x-1)·(x-3)·(3x+1)

• f(x) = x⁴ +3x² -2x + 1 ∈ ℚ[x] is irreducible. There are two options, f(x) = linear·cubic or quadratic·quadratic.

1. f(x) = linear·cubic ⇒ there exist a zero or root associated with the linear factor, but any root r/s must have r = ±1, s = ±1, but they are not roots of f(x). f(1) = 3 ≠ 0, f(-1) = 7 ≠ 0.
2. x⁴ +3x² -2x + 1 = quadratic·quadratic =[f(x) is monic] (x² +ax +b)(x² +cx +d) = x⁴ + (a + c)x³ + (b + ac + d)x² + (ad +bc)x + bd ⇒ bd = 1, a + c = 0, b + ac + d = 3, ad + bc = -2.

bd = 1 ⇒ b = d = 1 or b = d = -1.

If b = d = 1 ⇒[ad + bc = -2] a + c = -2 ⊥ a + c = 0. Otherwise, b = d = -1 ⇒[ad + bc = -2] -a -c = -2 ⇒ a + c = 2 ⊥ a + c = 0.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.