Isomorphism Theorems for Rings II

“If you are going through hell, be tough and keep going, but if you are in a big, deep, ugly shithole, stop digging,” Matthew retorted, but what he meant, not even he knew for sure, but it sounded cool and super positive though, Apocalypse, Anawim, #justtothepoint.

Definition

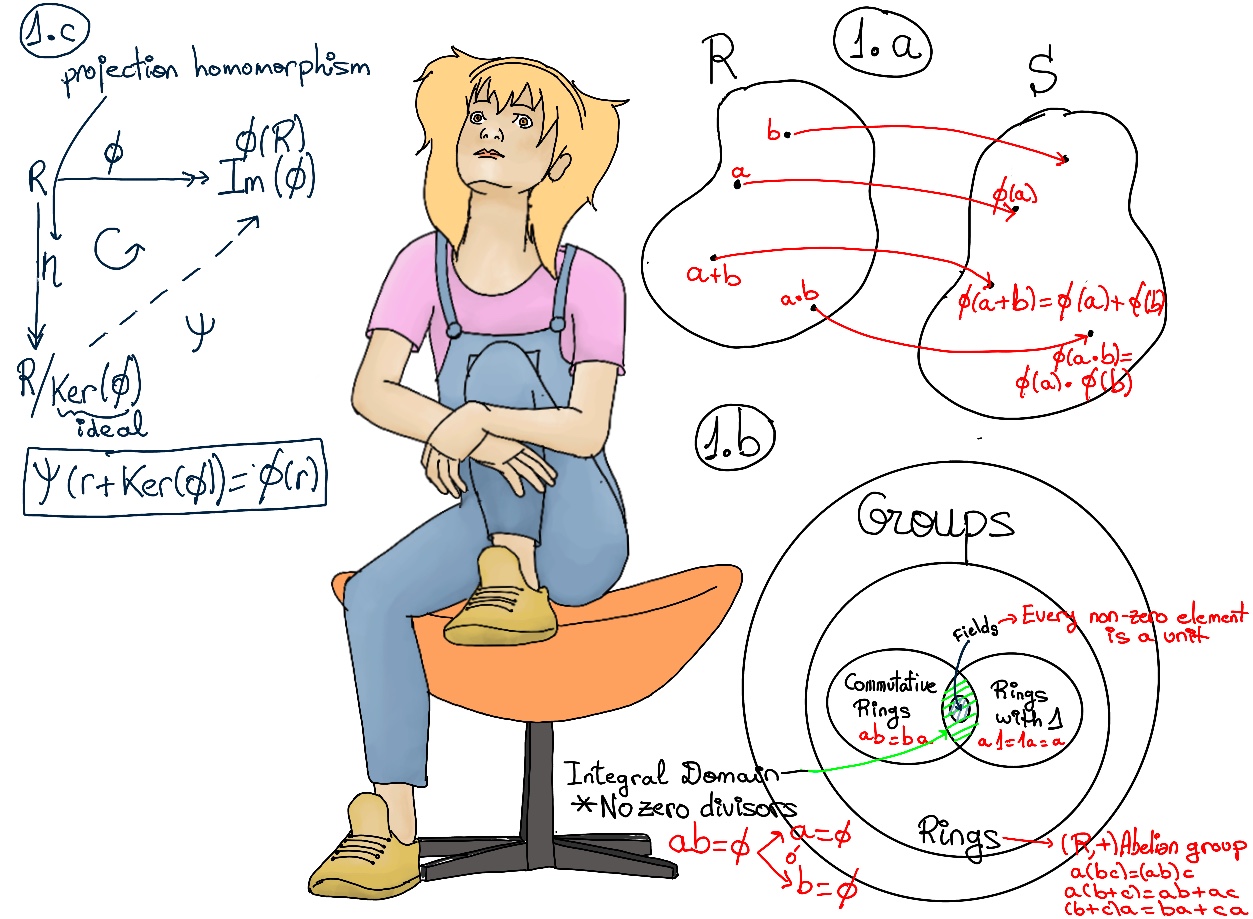
A ring homomorphism Φ from a ring R to a ring S is a structure-preserving function or mapping between two rings. More explicitly, it is a function Φ: R → S such that Φ is addition, multiplication, and unit (multiplicative identity) preserving, Φ(a + b) = Φ(a) + Φ(b), Φ(ab) = Φ(a)Φ(b), Φ(1_R) = 1_S, ∀a, b ∈ R. Figure 1.a.

💣In our original definition, a ring does no need to have a multiplicative identity, other authors define a ring to have a multiplicative identity and without the requirement for a multiplicative identity is instead called a rng, a non-unital ring or pseudoring. Φ(1_R) = 1_S only applies when a ring do have a multiplicative identity.

1. A ring isomorphism is a ring homomorphism that is both one-to-one and onto. It is used to show that two rings are algebraically identical.
2. The kernel of a ring homomorphism is the set of elements of R which are mapped to zero, Ker(Φ) = {r ∈ R| Φ(r) = 0}, where 0 is the additive identity.
3. The image of a ring homomorphism is the set of elements in the codomain S that are imaged of some elements in the domain R, im(Φ) = Φ(R) = {s ∈ S | s = Φ(r) for some r ∈ R}.  

Theorem. There is a unique or canonical ring homomorphism from the ring of integers to any ring. Let R be a ring with unity or multiplication identity 1 (or just a ring depending on your definition, ring versus rng - a non-unital ring or pseudoring-).

Proof.

1. There is at least one. The mapping Φ: ℤ → R defined by Φ(n) = n·1_R (where 1_R is the unit element in R) is a ring homomorphism. Φ(m + n) = (m + n)·1_R = m·1_R + n·1_R = Φ(m) + Φ(n). Φ(mn) = (mn)·1_R = (m·1_R)(n·1_R) = Φ(m)·Φ(n), Φ(1) = 1·1_R = 1_R.
2. Suppose Φ: ℤ → R is a ring homomorphism ⇒ Φ(1) = 1_R. Φ(0) = Φ(0 + 0) = Φ(0) + Φ(0) ⇒ Φ(0) = 0. Besides, 0 = Φ(0) = Φ(1 + (-1)) = Φ(1) + Φ(-1) ⇒ Φ(-1) = -Φ(1) = -1_R.
3. If n ∈ ℤ⁺, n = 1 + 1 + ··_{n times}·· + 1, Φ(n) = Φ(1) + Φ(1)+ ··_{n times}·· + Φ(1) = 1_R + 1_R+ ··_{n times}·· + 1_R = n·1_R
4. If n ∈ ℤ^-, Φ(-n) = -Φ(n) ⇒[-n ∈ ℤ⁺, Φ(-n) = (-n)·1_R] Φ(n) = -Φ(-n) = -(-n)·1_R = n·1_R∎ Uniqueness, Φ(n) = n·1_R ∀n ∈ ℤ.

Theorem. Every ring with unity has a subring isomorphic to either ℤ or ℤ_n. Let R be a ring (or a ring with unity depending on your definition). If Char(R) = n, then R contains a subring isomorphic to ℤ_n. If Char(R) = 0, then R contains a subring isomorphic to ℤ.

Proof.

Let 1 be the unity of R. The previous result shows that Φ: ℤ → R, Φ(n) = n·1_R is a homomorphism ⇒ [By the First Isomorphic Theorem for Rings] ℤ/Ker(Φ) ≋ Φ(ℤ).

Recall Let Φ: R → R' be a ring homomorphism and S be a subring of R ⇒ Φ(S) is a subring of R'. In particular, Φ(R) is a subring of R’.

Ker(Φ) = ⟨n⟩ where n is the additive order of 1_R, that is, Φ(n) = n·1_R = 1_R + 1_R + ··_{n times}·· + 1_R = 0_R ⇒ If Char(R) = n, Φ(ℤ) ≋ ℤ/⟨n⟩ ≋ ℤ_n, hence R contains a subring, namely Φ(ℤ), isomorphic to ℤ_n. Otherwise, if Char(R) = 0, Φ(ℤ) ≋ ℤ/⟨0⟩ ≋ ℤ.

Recall, by Characteristic of a Ring with Unity. If 1 has infinite order under addition, then char(R) = 0. If 1 has order n under addition, then char(R) = n.

Exercises

• Find all ring homomorphisms Φ: ℚ → ℚ. Let’s set Φ(1) = a. Then, a² = a·a = Φ(1)·Φ(1) = Φ(1·1) = Φ(1) = a, that is, a² = a ⇒[This equation in the rational numbers field has only two solutions] a = 0 or a = 1.

1. a = 0. ∀x ∈ ℚ, Φ(x) = Φ(x·1) = Φ(x)·Φ(1) = Φ(x)·a = Φ(x)·0 = 0, Φ is the trivial ring homomorphism.
2. a = 1. Take n ∈ ℕ, Φ(n) = Φ(1 + 1 + ··_{n times}·· + 1) = Φ(1) + Φ(1) + ··_{n times}·· + Φ(1) = nΦ(1) = n·1 = n.

Φ(0) =[Φ is a ring homomorphism] 0.
0 = Φ(n + (-n)) = Φ(n) + Φ(-n) = n + Φ(-n) ⇒ n + Φ(-n) = 0 ⇒ Φ(-n) = -n.
1 = Φ(1) = Φ(1/n + ··_{n times}·· + 1/n) = Φ(1/n) + ··_{n times}·· + Φ(1/n) = nΦ(1/n) ⇒ nΦ(1/n) = 1 ⇒ Φ(1/n) = 1/n.
∀m/n ∈ ℚ, Φ(m/n) = Φ(m·1/n) = Φ(m)Φ(1/n) = m·1/n = m/n, Φ is the identity. Therefore, a ring homomorphism over rational numbers is either the trivial homomorphism or the identity.

• Find all ring homomorphism Φ: ℤ₁₂ → ℤ₂₈.

Let’s set Φ(1) = a ⇒ a² = a·a = Φ(1)·Φ(1) = Φ(1·1) = Φ(1) = a ⇒ a² = a ⇒[An idempotent element of a ring is an element a such that a² = a, e.g., 0, 1, 3, and 4 are idempotent elements of ℤ/6ℤ. A trivial idempotent refers to either of the elements 0 and 1, which are always idempotent.] 0, 1, 8, and 21 are idempotent elements of ℤ₂₈, so a = Φ(1) = 0, 1, 8, or 21.

Recall (group abstract algebra and group homomorphisms) that |Φ(1)| | |1| and we are talking about the additive order (inside the additive group) of Φ(1) -ℤ₂₈- and 1 -ℤ₁₂- respectively ⇒ |Φ(1)| = |a| | 12 (= |1| in ℤ₁₂) ⇒ |a| ∈ {1, 2, 3, 4, 6, 12}.

Besides, recall (cyclic groups) that in ℤ_n, |k| = $\frac{n}{gcd(n, k)}$, and therefore n = 28, (a = 0, 1, 8 and 21), |0|_ℤ28 = 1, |1|_ℤ28 = 28 ∉ {1, 2, 3, 4, 6, 12}, |8|_ℤ28 = $\frac{n}{gcd(n, k)}= \frac{28}{gcd(28, 8)} = \frac{28}{4} = 7$ ∉ {1, 2, 3, 4, 6, 12}, and finally |21|_ℤ28 = $\frac{n}{gcd(n, k)}= \frac{28}{gcd(28, 21)} = \frac{28}{7} = 4$, so the only possibilities are a = 0 or 21.

1. Φ(1) = 0 ⇒ ∀n ∈ ℤ₁₂, Φ(n) = Φ(1 + 1 + ··_n·· + 1) = Φ(1) + Φ(1) + ··_n·· + Φ(1) = n·Φ(1) = n·0, and we are talking about the trivial ring homomorphism.
2. Φ(1) = 21 ⇒ ∀n ∈ ℤ₁₂, Φ(n) = 21n =[ℤ₂₈] -7n.

Corollary. ℤ_n is a homomorphic image of ℤ.

Proof.

There are two different approaches.

1. Consider the mapping Φ: ℤ → ℤ_n given by Φ(a) = a mod n = [a]. Since Φ(a + b) = [a + b] = [a] + [b] = Φ(a) + Φ(b), and Φ(ab) = [ab] = [a][b] = Φ(a)Φ(b) ∀a, b ∈ ℤ, Φ is a ring homomorphism from ℤ to ℤ_n. In fact, Φ is an epimorphism and ℤ_n is a homomorphic image of ℤ.

   If Φ: R → S ring homomorphism is also onto, then Φ is called an epimorphism and S is called a homomorphic image of R.

2. By the previous theorem’s proof, there is a unique or canonical ring homomorphism from the ring of integers to any ring. ∀n ∈ ℤ⁺, the map Φ: ℤ → ℤ_n given by Φ(a) = a mod n = [a] = a · 1 (e.g., in ℤ₄, 3·1 = 1 + 1 + 1 = 3 mod 4 = 3, 6·1 = 1 + 1 + 1 + 1 + 1 + 1 = 6 mod 4 = 2) is a ring homomorphism, and it is clearly onto.

Corollary. Every field has a subfield isomorphic either to ℤ_p or to ℚ. Let F be a field. If Char(F) = p, then F contains a subfield isomorphic to ℤ_p. If Char(F) = 0, then F contains a subfield isomorphic to ℚ.

Proof:

Recall that a field is a commutative ring with unity such that each nonzero element has a multiplicative inverse, e.g., every finite integral domain, ℤ_p (p prime), ℚ, ℝ, and ℂ. A field has characteristic zero or characteristic p with p prime.

By the previous result, if Char(F)=p, then F contains a subring isomorphic to ℤ_p and we are done.

If Char(F) = 0, then F has a subring S isomorphic to ℤ. Φ: ℤ → F, Φ(n) = n·1_F, Φ is a ring homomorphism, and by the first isomorphism theorem for rings, ℤ/⟨0⟩ ≋ ℤ ≋ Φ(ℤ), i.e., S = Φ(ℤ) is a subring of F isomorphic to ℤ. Therefore, S = {n·1_F: n ∈ ℤ} ⊆_{subring of} F.

Let T =[Since a field must have all multiplicative inverses of n·1_F, n ≠ 0] {ab^-1 | a, b ∈ S, b ≠ 0}. Claim: T is a subfield of F (it is left as an exercise) and T ≋ ℚ.

Recall that a field F is a commutative (the multiplication is commutative) division ring.

Let Φ be the mapping: T → ℚ, Φ(ab^-1) = a/b. More precisely, it would be (m·1_F)(n·1_F)^-1 → m/n.

1. Φ is well defined. Similar argument Φ is injective.

2. Φ is a ring homomorphism. Φ(ab^-1 + cd^-1) =[Since (F,·) is commutative, ab^-1 + cd^-1 = adb^-1d^-1 + bcb^-1d^-1] Φ((ad + bc)(bd)^-1) = (ad + bc)/bd = ad/bd + bc/bd = a/b + c/d = Φ(ab^-1) + Φ(cd^-1).

3. Φ((ab^-1)(cd^-1)) =[Since (F,·) is commutative] Φ(acb^-1d^-1) = Φ((ac)(bd)^-1) = ac/bd = (a/b)(c/d) = Φ(ab^-1)Φ(cd^-1)

4. Φ is injective. Suppose Φ(ab^-1) = Φ(cd^-1) ⇒ a/b = c/d ⇒ ad = cb ⇒ adb^-1 = cbb^-1 ⇒[Since (F,·) is commutative] ab^-1d = c ⇒ ab^-1 = cd^-1.

5. By construction, Φ is onto ∎

Since the intersection of all subfields of a field is a subfield, too, every field has a smallest subfield called the prime subfield of the field.

If Char(F)=p, the prime subfield is isomorphic to ℤ_p. Otherwise, if Char(F) = 0, the prime subfield is isomorphic to ℚ.

Third ring isomorphism theorem. Let R be a ring with ideals I ⊆ J ⊆ R. Then, $\frac{R/I}{J/I} ≋ R/J$.

Proof:

Let’s define a map Φ: R/I → R/J given by Φ(r + I) = r + J.

1. Φ is well-defined. Suppose a + I = b + I ∈ R/I ⇒ a - b ∈ I ⊆ J ⇒ a -b ∈ J ⇒ a + J = b + J ⇒ Φ(a + I) = Φ(b + I).
2. Φ is a ring homomorphism. Φ((a + I) + (b + I)) =[By definition of addition of cosets] Φ((a + b) + I) = (a + b) + J = (a + J) + (b + J) = Φ(a + I) + Φ(b + I). Φ((a + I)· (b + I)) =[By definition of multiplication of cosets] Φ(ab + I) = ab + J = (a + J) · (b + J) = Φ(a + I)·Φ(b + I).
3. ∀r + I ∈ Ker(Φ) ↭ Φ(r + I) = 0 + J ↭ r + J = 0 + J = J ↭ r ∈ J ↭ r + I ∈ J/I, and therefore, Ker(Φ) = J/I. By construction, Φ is onto.
4. By the first isomorphism theorem, $\frac{R/I}{J/I} ≋ R/J$.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.