Isomorphism Theorems for Rings

Then, she continued, “You’re a living proof against both evolutionary biologists and believers, that is, in itself, quite remarkable. You are physically repulsive, morally reprehensible and bankrupt, intellectually impaired, socially awkward, embarrassing, and inept, religiously condemned, psychologically handicapped, diagnosed as an incurable narcissist, subtle as a brick to the head, sensitive as an ATM machine, rude, gross, pathetic, and you even smell,” Apocalypse, Anawim, #justtothepoint.

The reader may want to recall that in the case of a homomorphism Φ of groups, Φ: G → G’, the cosets of ker(Φ) have the structure of a group (the quotient group, G/Ker(Φ)≋ Φ(G)). In this case, ker(Φ) is the identity of the associated quotient group. Futhermore, every kernel is a normal subgroup of the domain (Ker(Φ) ◁ G) and every normal subgroup can be realized as the kernel of some group homomorphism. Is there anything similar for rings?

Let (R, +, ·) be a ring, let A be an ideal of R. Let R/A be the coset space of R modulo A with respect to addition +. Let’s define two operations:

1. ∀r,s ∈ R: (r + A) + (s + A) = (r + s) + A
2. ∀r,s ∈ R: (r + A) · (s + A) = (r · s) + A The algebraic structure (R/A, +, ·) is called the quotient ring of R by A. In other words, the additive quotient group R/A is a ring under the previously defined operations.

Theorem. Every ideal of a ring R is the kernel of a ring homomorphism of R.

Proof.

Let A be an ideal of a ring R. The function η: R → R/A defined by η(r) = r + A is a ring homomorphism (it is called the canonical o natural homomorphism for A) and its kernel is A.

∀r, s ∈ A, η(r) + η(s) = (r + A) + (s + A) = (r + s) + A = η(r + s)

η(r)η(s) = (r + A)(s + A) = rs + A = η(rs), and therefore Φ is a ring homomorphism.

Futhermore, r ∈ ker(η) ↭ η(r) = 0_R + A = A ↭ η(r) = r + A = A ↭ r ∈ A ↭ Ker(μ) = A.

First Isomorphism Theorem for Rings. Let R and S be rings, and let Φ be a ring homomorphism from R to S. Then, R/Ker(Φ) ≋ Φ(R), i.e., the mapping ψ: R/Ker(Φ) → Φ(R), given by r + Ker(Φ) → Φ(r) is an isomorphism, (Figure 1.c).  

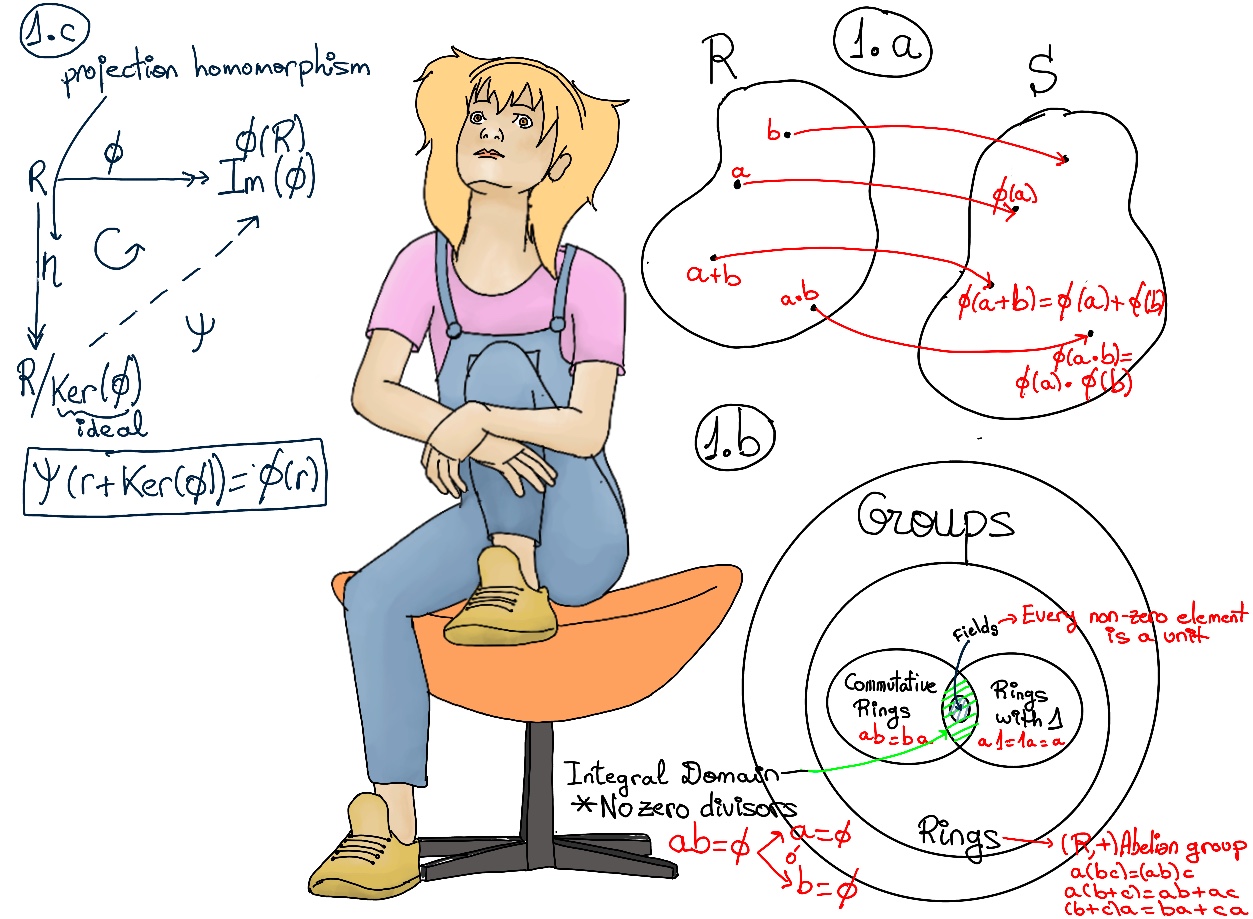
Proof: Let’s define the mapping ψ: R/Ker(Φ) → Φ(R) given by ψ(r + Ker(Φ)) = Φ(r).

1. Well-defined. Let’s take two representatives of the same cosets, so suppose that r + Ker(Φ) = r’ + Ker(Φ) ⇒ r’- r ∈ Ker(Φ) ⇒ Φ(r’ -r) = 0. ψ(r + Ker(Φ)) = Φ(r) = Φ(r) + 0 = [Φ(r’ -r) = 0] Φ(r) + Φ(r’ -r) = Φ(r + r’ -r) =[(R, +) is an Abelian group] Φ(r’) = ψ(r’ + Ker(Φ)).
2. Ring homomorphism. ψ((a + Ker(Φ) + (b + Ker(Φ)) = ψ((a + b) + Ker(Φ)) = Φ(a + b) = Φ(a) + Φ(b) = ψ(a + Ker(Φ)) + ψ(b + Ker(Φ)). Besides, ψ((a + Ker(Φ)) · (b + Ker(Φ)) = ψ((a · b) + Ker(Φ)) = Φ(a · b) = Φ(a) · Φ(b) = ψ(a + Ker(Φ)) · ψ(b + Ker(Φ)).
3. Injective. Suppose r + Ker(Φ) ∈ Ker(ψ) ⇒ ψ(r + Ker(Φ)) = 0, we also know that ψ(r + Ker(Φ)) = Φ(r), therefore Φ(r) = 0, hence r ∈ Ker(Φ) ⇒ r + Ker(Φ) = 0 + Ker(Φ). Ker(ψ) = 0 + Ker(Φ) = Ker(Φ), that is, the kernel is the trivial identity in the coset group R/Ker(Φ), so ψ is injective.
4. Surjective. Suppose an element from the image, Φ(r) ∈ Φ(R)=Im(Φ), obviously ψ(r + Ker(Φ)) = Φ(r), in other words, it was built-in to be surjective.

Examples

• Let Φ: ℤ → ℤ_n, Φ(m) = [m]_ℤn is clearly an onto (im(Φ) = ℤ_n) ring homomorphism. Ker(Φ) = {m ∈ ℤ: Φ(m) = [0]_ℤn} = {m ∈ ℤ: m ≡ 0 (mod n)} = nℤ. Therefore, by the First Isomorphism Theorem for Rings, ℤ/nℤ ≋ ℤ_n.

• Let Φ: ℤ[x] → ℤ given by Φ(f(x)) = f(0). It is a ring homomorphism with Ker(Φ) = ⟨x⟩, Φ is obviously onto (∀n ∈ ℤ, n ∈ ℤ[x] is a polynomial of degree zero and Φ(n) = n). Therefore, by the First Isomorphism Theorem for Rings, ℤ[x]/⟨x⟩ ≋ ℤ. ℤ is an integral domain but not a field, then the ideal ⟨x⟩ is prime (A is prime ↭ R/A integral domain) but not maximal (R/A is a field ↭ A is maximal) in ℤ[x].

  Ker(Φ) = {f(x) ∈ ℤ[x], f(x) = a₀+a₁x + ··· + a_nxⁿ| Φ(f(x)) = f(0) = a₀ = 0} = {f(x) ∈ ℤ[x], f(x) = a₁x + a₂x² + ··· + a_nxⁿ} = {f(x) ∈ ℤ[x], f(x) = x(a₁ + a₂x + ··· + a_nx^n-1)} = {xq(x)| q(x)∈ ℤ[x]} = ⟨x⟩.

• Fix an arbitrary real number a. Consider the evaluation map μ: ℝ[x] → ℝ, μ(f) = f(a). It is a surjective ring homomorphism, e.g., it is surjective, ∀b ∈ ℝ, let f(x) be the constant polynomial, f(x) = b, then μ(f) = f(a) = b.

Ker(μ) = {f ∈ ℝ[x] : μ(f) = f(a) = 0}. By the factor theorem, f(a) = 0 ↭ (x -a) is a factor of f, hence Ker(μ) = {(x -a)g(x) | g ∈ ℝ[x]} = ⟨x-a⟩. By the first isomorphism theorem, ℝ[x]/⟨x-a⟩ ≋ ℝ

• Φ: ℝ[x] → ℂ, given by f → f(i). Φ is a surjective ring homomorphism. ∀x ∈ ℂ, x = a + bi, consider the polynomial a + bx, Φ(a + bx) = a + bi = x, so Φ is surjective.

Claim: Ker(Φ) = ⟨x² + 1⟩

1. ⟨x² + 1⟩ ⊆ Ker(Φ). x² + 1 ∈ Ker(Φ) because Φ(x² +1) = i² + 1 = -1 + 1 = 0. Besides, ∀Φ ring homomorphism, Ker(Φ) is an ideal of R, in our particular case, ℝ[x], therefore every polynomial multiple of x² +1 is in the Kernel, so ⟨x² + 1⟩ ⊆ Ker(Φ)
2. f ∈ Ker(Φ) ⇒ By the division algorithm, f = (x² +1)q(x) + r(x) where r = 0 or deg(r) < 2. Let’s apply Φ, Φ(f) = Φ(x² +1)Φ(q(x)) + Φ(r(x)) ⇒[f and x²+1 are in the kernel] 0 = 0·Φ(q(x)) + Φ(r(x)) ⇒ Φ(r(x)) = 0 ⇒[deg(r)<2, r = a +bx, Φ(r) = a + bi = 0 ⇒ a = b = 0] r = 0 ⇒ f = (x² +1)q(x) ⇒ f ∈ ⟨x² +1⟩.

By the first isomorphism theorem for rings, ℝ[x]/⟨x²+1⟩ ≋ ℂ

Second Isomorphism Theorem for Rings. Let R be a ring, I be a subring of R, and J be an ideal of R. Then:

1. I + J = {i + j: i ∈ I, j∈ J} is a subring of R
2. I ∩ J is an ideal of I.
3. $\frac{I}{I ∩ J} ≋ \frac{I + J}{J}$

Proof.

• I + J is a subring of R. I is a subring (1 ∈ I), J is an ideal of R (an ideal is an Abelian subgroup of R, 0 ∈ J) ⇒ 1 = 1 + 0 ∈ I + J.

∀ i₁ + j₁, i₂ + j₂ ∈ I + J, (i₁ + j₁) - (i₂ + j₂) = (i₁ -i₂) + (j₁ -j₂) ∈ I + J. (i₁ + j₁)·(i₂ + j₂) = i₁i₂ + (i₁j₂ + j₁i₂ + j₁j₂) ∈ I + J because i₁i₂ ∈ I and i₁j₂ + j₁i₂ + j₁j₂ ∈ J (J is an ideal of R and it absorbs these products) ⇒ I + J is a subring of S.

• I ∩ J is an ideal of I. I ∩ J is not empty since 0 is contained in I and J. Besides, ∀a₁, a₂ ∈ I ∩ J, a₁ + a₂ ∈ I ∩ J since I and J are both closed under addition.

Suppose a ∈ I ∩ J, b ∈ I, ab ∈ I ∩ J and ba ∈ I ∩ J?

a ∈ I ∩ J ⇒ a ∈ I, a ∈ J, [J is an ideal of R] ab ∈ J, [I is subring, so there’s closure under multiplication, a ∈ I, b ∈ I] ab ∈ I ⇒ ab ∈ I ∩ J.

Mutatis mutandis, the same reasoning applies to ba ∈ I ∩ J.

• Let’s define the following map, Φ: I → I+J/J, Φ(a) = a + J.

1. Φ is homomorphism. Φ(a + b) = (a + b) + J = [By definition of addition in quotient ring] (a + J) + (b + J) = Φ(a) + Φ(b). Similarly, Φ(ab) = Φ(a)Φ(b).

2. Φ is onto. Suppose an arbitrary coset of the codomain a + J ∈ I + J/J, where a ∈ I + J, that is, a = i + j, i ∈ I, j ∈ J ⇒ a + J = (i + j) + J = [j ∈ J, aH = H ↭ a ∈ H] i + J. Therefore, Φ(i) = i + J = a + J.

3. Ker(Φ) = I ∩ J

   Suppose a ∈ I ∩ J ⇒ a ∈ I, a ∈ J. Because a ∈ I, our domain, it makes sense apply to it our homomorphism, Φ(a) = a + J = [a ∈ J] 0 + J = J, therefore a ∈ Ker(Φ) ⇒ I ∩ J ⊆ Ker(Φ)

   Suppose a ∈ Ker(Φ), Ker(Φ) is an ideal of the domain of Φ, that is, I, so a ∈ I. Besides Φ(a) = [Definition of the map Φ] a + J = [a ∈ Ker(Φ)] 0 + J = J ⇒ a ∈ J ⇒ a ∈ I ∩ J ⇒ Ker(Φ) ⊆ I ∩ J ⇒[We have previously demonstrated that I ∩ J ⊆ Ker(Φ)] Ker(Φ) = I ∩ J.

4. By the first Isomorphic Theorem of Ring, $\frac{I}{Ker(Φ)}=\frac{I}{I ∩ J} ≋ Im(Φ)$ = [Φ is onto] $\frac{I + J}{J}$ Therefore, $\frac{I}{I ∩ J} ≋ \frac{I + J}{J}$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.