Polynomial Rings II. Principal ideal domains.

My appearance had improved substantially, but my pictures could still be sold to scare people, summon the devil, and kill the elderly. I was notice immediately, so many of my coworkers felt embarrassed and avoid hanging with me like eating shit or alien foreskin, Apocalypse, Anawim, #justtothepoint.

Recall

Definition. Let R be a commutative ring. A polynomial ring is a ring formed from the set of polynomials in one or more indeterminates or variables with coefficients in R. R[x] = {a_nxⁿ + a_n-1x^n-1+ ··· + a₁x + a₀ | a_i ∈ R, n ∈ ℤ⁺}, e.g. 2x³+ 7x² +4∈ ℤ[x], ²⁄₃x² + 4x -7 ∈ ℚ[x].

Division Algorithm. Let F be a field, f(x), g(x) ∈ F[x], g(x) ≠ 0. Then, there exists unique polynomials q(x) and r(x) ∈ F[x] such that

1. f(x) = g(x)q(x) + r(x)
2. Either r(x) = 0 or deg(r(x)) < deg(g(x))., e.g., in ℤ₂[x], f(x) = x⁴ + x³ +x +1, g(x) = x² + x, f(x) = x⁴ + x³ +x +1 = (x² + x)x² + (x + 1) where deg(x + 1) < 2; or in ℤ₅[x], f(x) = x³ + 2x² +3x +4, g(x) = x² +1, x³ + 2x² +3x +4 = (x² + 1)(x + 2) + (2x + 2) and deg(2x + 2) < 2.

Definition. Let F be a field, let f, g ∈ F[x]. We say that g divides f (written g | f) or g is a factor of f if r is the zero polynomial.

Definition. A root of f(x) ∈ F[x] is an element α ∈ F such that f(α) = 0. Remark: f(x) ∈ ⟨x⟩ ↭ 0 is a root of f(x). Roots may exist in bigger or “extended” rings, e.g., 2x has no root in ℤ, but it has a root in ℚ, namely ¹⁄₂, x² +1 has no roots in ℝ, but it has roots in ℂ, $\sqrt{i}$.

Factor Theorem. Let F be a field, and f ∈ F[x]. An element α ∈ F is a zero or a root of f (that is f(α) = 0) if and only if (x -α)|f(x), that is, there exist some q ∈ F[x] such that f(x) = (x - α)q(x).

Proof. By the division algorithm f(x) = (x - α)q(x) + r(x) where either r(x) = 0 or deg(r)< deg(x -α) = 1 ⇒ deg(r) = 0 ⇒ r is a constant.

Futhermore, f(α) = (α - α)q(α) + r(α) = r(α) ⇒ α is a zero (f(α) = 0) if and only if r is the zero polynomial. ∎

This result is directly derived from the factor Theorem. Let F be a field, and f ∈ F[x]. If f(x) has degree n and r₁, r₂,…, r_n are the roots of f(x) in F, then f(x) can be uniquely represented as follows, f(x) = a_n(x - r₁)(x - r₂)···(x - r_n)where a_n is the leading coefficient of f(x).

Examples: f(x) = x² + 4 ∈ ℂ[x] has two roots, 2i and -2i ⇒ f(x) = (x - 2i)(x + 2i) -Figure 1.e.- g(x) = 2x² + 4x + 5 ∈ ℤ₇[x] has two roots, 2 and 3 ⇒ g(x) = 2(x -2)(x -3) where 2 = a₂ is the leading coefficient of g(x).

Remainder Theorem. Let F be a field, α ∈ F, and f ∈ F[x]. Then, f(α) is the remainder of the division of f(x) by x-α.

Proof. By the division algorithm f(x) = (x - α)q(x) + r(x) where r(x) = 0 or deg(r) < deg(x -α) = 1 ⇒ deg(r) = 0 ⇒ r is a constant.

Futhermore, f(α) = (α - α)q(α) + r(α) = r(α) ∎

Example: f(x) = x⁷ -6x⁵ +4x⁴ -x² +3x -7 ∈ ℚ[x], f(2) = -5 ⇒ f(x) = q(x)(x -2) -5 (Figure 1.d.). g(x) = x⁵ +3x⁴ + x³ + x² +2x +2 ∈ ℤ₅[x], 1 is root ⇒ g(x) = q(x)(x -1).  

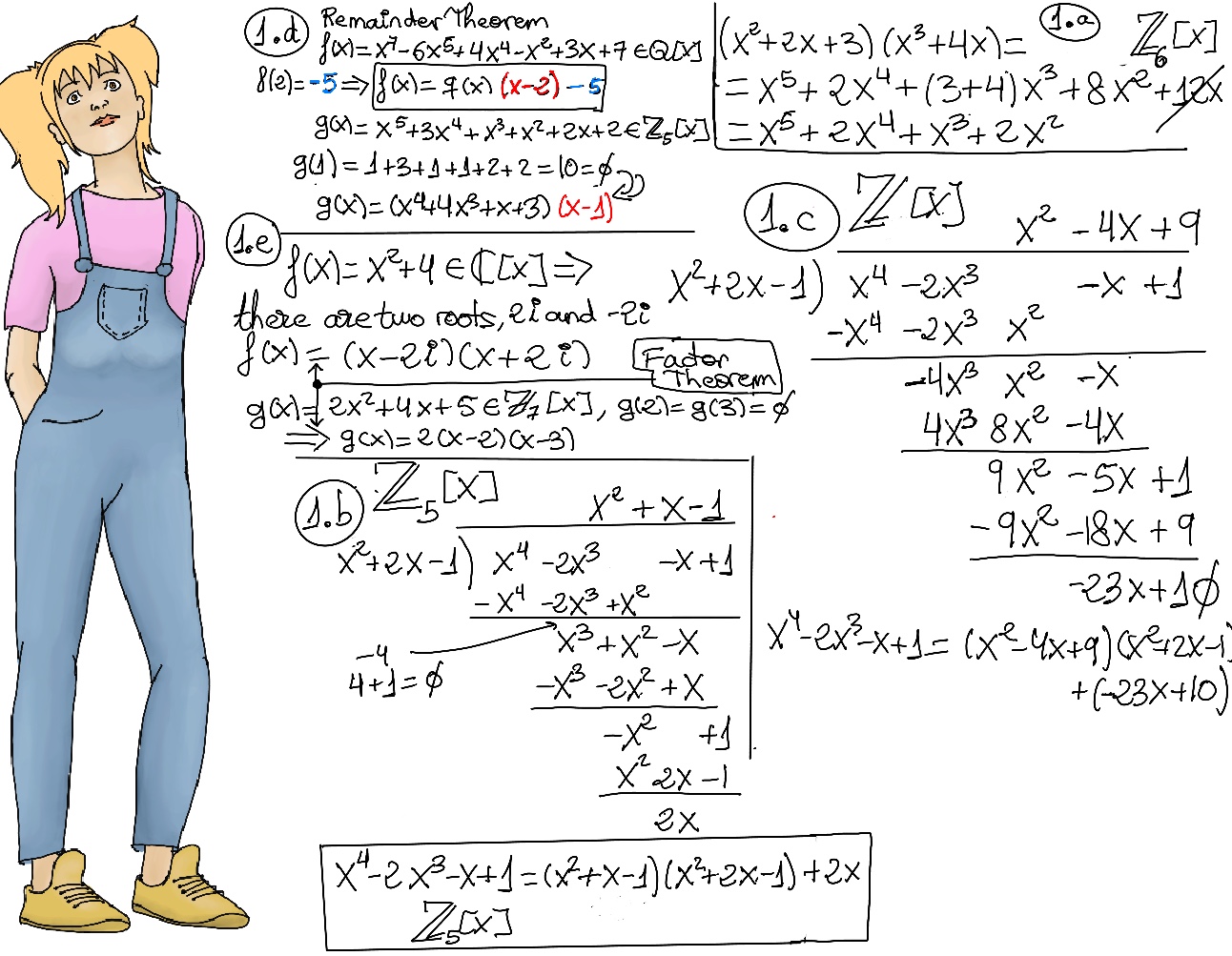
Corollary. A degree n polynomial over a field F has at most n distinct zeros in F, counting multiplicity.

Proof. Let’s proceed by induction on the degree of the polynomial, n.

A polynomial of degree n = 0 over a field has no zeros.

If deg(f(x)) = 1 ⇒ f(x) = ax + b, a ≠ 0. Suppose α, β ∈ F are zeros of f(x) ⇒ aα + b = f(α) = 0 = f(β) = aβ + b ⇒ aα + b = aβ + b ⇒[F field, the cancellation law applies] aα = aβ ⇒[F field, a ∈ F, a ≠ 0, a has an inverse, let’s multiply by a^-1] α = β ⇒ f has at most 1-zero.

Suppose, f(x) is a polynomial of degree n over a field F, a is a zero of multiplicity k ⇒ f(x) = (x -a)^kq(x) and q(a) ≠ 0 ⇒[F field ⇒ integral domain and def(f·g) = deg(f)+deg(g)] n = k + deg(q) ⇒ k ≤ n. There are two possibilities:

1. If f has no zeros other than a, we are done.
2. Let’s suppose there exist b ≠ a, b is zero of f ⇒ 0 = f(b) = (b - a)^kq(b) ⇒ b is a zero of q, too, with the same multiplicity as it has for f🚀, and by induction hypothesis q has at most deg(q) = n -k zeros, counting multiplicity ⇒ f has at most k + (n-k) zeros counting multiplicity ∎

   🚀 Let m be the multiplicity of b in q(x) ⇒ q(x) = (x-b)^ms(x), s(x) ∈ F[x], s(b) ≠ 0 ⇒ f(x) = (x-a)ⁿ(x-b)^ms(x) ⇒ b is a zero of f of multiplicity at least m. Suppose for the sake of contradiction, b is a zero of f of multiplicity greater than m ⇒ b is a zero of f(x)/(x-b)^m = (x-a)ⁿs(x) ⇒ 0 = (b -a)ⁿs(b) ⇒[b ≠ a] s(b) = 0⊥ Therefore, b is a zero of f of multiplicity m.

Examples:

• This result may not hold if F is not a field, e.g., in ℤ₁₂[x], f(x) = x² + 1, deg(f) = 2, but it has four distinct zeros, namely 1, 5, 7, and 11, and there is no a unique factorization, f(x) = (x -1)(x -11) = (x -5)(x -7).

• Let’s find all complex zeros of xⁿ -1.

De Moivre’s formula states that ∀x ∈ ℝ, n ∈ ℤ, (cosx + isinx)ⁿ = cos(nx) + isin(nx) where i is the imaginary unit (i² = -1) ⇒ A nth root of unit are e^(2kπi/n) = cos(2kπ/n) + isin(2kπ/n), k = 0, 1, ···, n -1, so there are already n, and by the previous corollary, we can see there are no other roots or zeroes of xⁿ - 1.

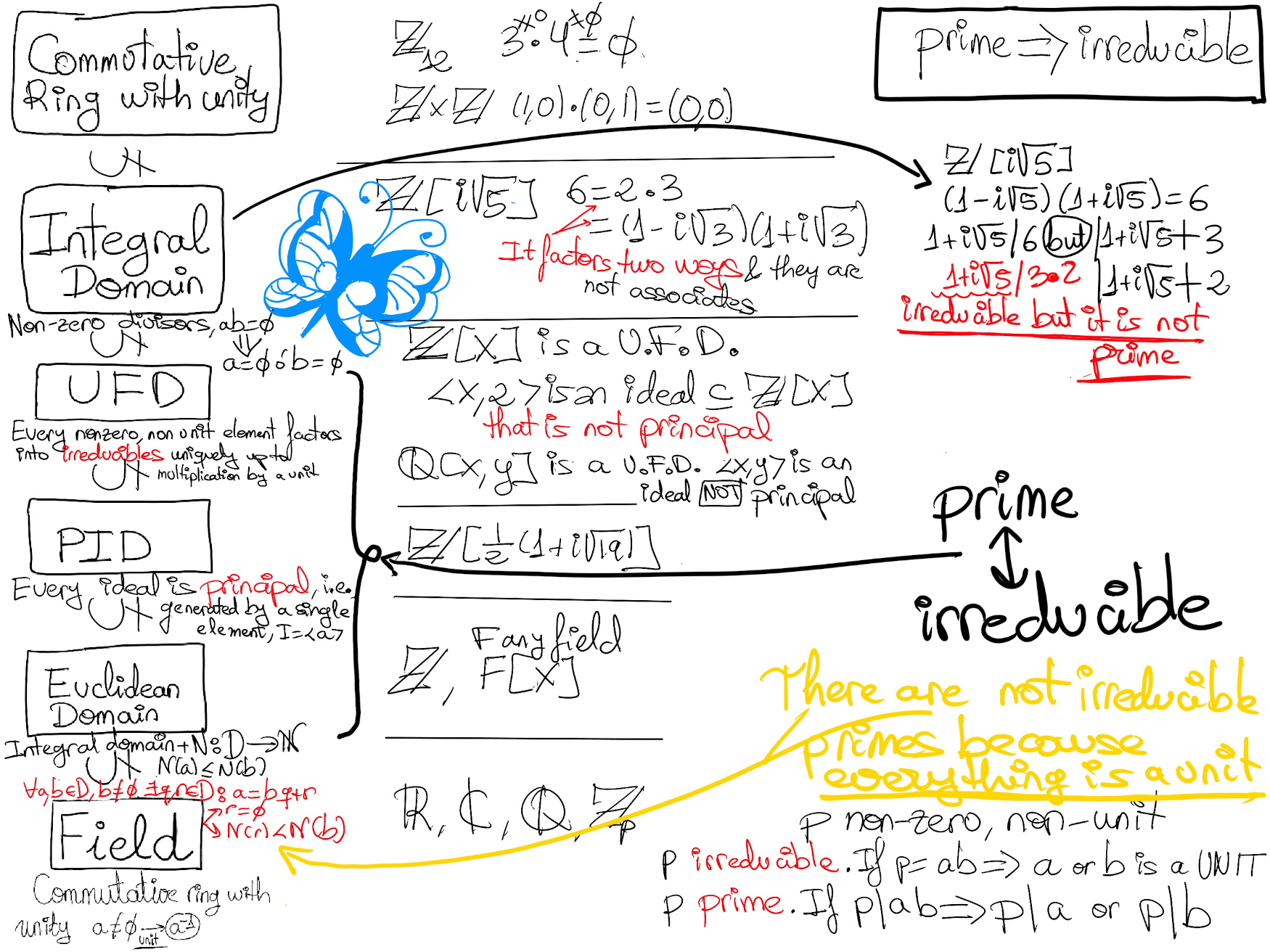
Definition. A principal ideal is an ideal generated by a single element a of R though multiplication by every element of R, ⟨a⟩ = Ra = {ra | r ∈ R} = {ar | r ∈ R}. A ring R is a principal ideal domain (PID) if it is an integral domain such that every ideal of R is a principal ideal, that is, has the form ⟨a⟩ = Ra = {ra | r ∈ R} = {ar | r ∈ R}, e.g., ℤ, and if F is a field, both F and F[x] are PIDs, but ℤ[x] or F[x₁, x₂,···, x_n], n ≥ 2 are not PIDs.

Proposition. The ring of integers ℤ is a PID.

Proof.

ℤ is a integral domain. Therefore, we only need to prove that every ideal of ℤ is principal.

Let I be an ideal of ℤ. If I = {0}, then I = ⟨0⟩, so I is a principal ideal.

Otherwise, I ≠ {0}, let a be the smallest integer such that a > 0 and a ∈ I. We claim that I = ⟨a⟩.

1. Since a ∈ I ⇒ [I is an ideal] ⟨a⟩ ⊆ I.
2. Conversely, ∀b ∈ I, by the division algorithm, ∃q, r ∈ ℤ: b = aq + r, q, 0 ≤ r < q ⇒ r = b - aq ⇒ [b ∈ I, aq ∈ I because I is an ideal and a ∈ I] r ∈ I, since a is the smallest positive element of R ⇒ r = 0 ⇒ b = aq ⇒ b ∈ ⟨a⟩ ⇒ I ⊆ ⟨a⟩ ⇒ I = ⟨a⟩.

Proposition. If F is a field, then F is a PID.

Proof.

F field ⇒ F is an integral domain. Therefore, we only need to prove that every ideal of F is principal.

If I is a ring, and it has a non-zero element, say a ≠ 0, a ∈ I ⇒ ∀b ∈ F, b = [F is a field, every non-zero element has a multiplicative inverse ∃a^-1: a·a^-1 = a^-1·a = e_F, and obviously ba^-1 ∈ F, a ∈ I, I ideal] (ba^-1)a ∈ I ⇒ ∀b∈ F, b ∈ I ⇒ I = F. As a consequence, the only ideals of any field F are the trivial ideal and the entire field, {0} = ⟨0⟩ and F = ⟨1⟩.

Proposition. If F is a field, then the ring of polynomials F[x] is a PID.

Proof.

F field ⇒ F is an integral domain ⇒[Recall Let D be a commutative ring with unity 1. Then, D[x] is an integral domain if and only if D is an integral domain.] F[x] is an integral domain. Therefore, we only need to prove that every ideal of F[x] is principal.

Let I ∈ F[x] be an ideal. If I = {0}, then I = ⟨0⟩.

Otherwise, let g(x) ≠ 0 be a polynomial of minimum degree, that is, such that g(x) ∈ I, deg(g(x)) ≤ deg(p(x)) ∀p(x) ∈ I - {0}. We claim that I = ⟨g(x)⟩

1. Since g(x) ∈ I, I ideal ⇒ ⟨g(x)⟩ ⊆ I.
2. Let f(x) ∈ I, then by the division algorithm, f(x) = g(x)q(x) + r(x), where either r(x) = 0 or deg(r(x)) < deg(g(x)). Since r(x) = f(x) -g(x)q(x) ∈ I ⇒ [By assumption, g(x) is a polynomial of minimum degree] r(x) = 0 ⇒ f(x) = g(x)q(x) ⇒ f(x) ∈ ⟨g(x)⟩ ⇒ I ⊆ ⟨g(x)⟩ ⇒ I = ⟨g(x)⟩ ∎

Theorem. Let F be a field, I a nonzero ideal in F[x], and g(x) ∈ F[x]. Then, I = ⟨g(x)⟩ ↭ g(x) is a nonzero polynomial of minimum degree in I, that is, the smallest possible degree among the degrees of nonzero polynomials in I (the proof is provided for free on the previous theorem’s proof)

Counterexample: ℤ[x] is not a PID.

Proof. Let’s consider the ideal ⟨2, x⟩. This ideal is not principal.

Suppose for the sake of contradiction that I = <2, x> in ℤ[x] is principal ⇒ ∃f(x) ∈ ℤ[x] such that I = < f(x) >. As 2 ∈ I, there exists g(x) ∈ ℤ[x] such that 2 = f(x)g(x) ⇒ def(f(x)) + deg(g(x)) = deg(f(x)g(x)) = 0 ⇒ deg(f(x)) = deg(g(x)) = 0 ⇒ [2 = f(x)g(x)] ∃a, b ∈ ℤ: 2 = ab ⇒ f(x) = a = ±1 or ±2.

If a = ±1 then < 2, x > = < 1 > ⇒ ∃r(x), s(x) ∈ ℤ[x]: 1 = 2r(x) + xs(x). Evaluating these polynomials for x = 0, then 1 = 2r(0), so that r(0) = 1/2 ⊥ r(0) ∈ ℤ.

If a = ±2 then < 2, x > = < 2 > ⇒ ∃v(x) ∈ ℤ[x]: x = 2v(x). Then, v(x) = 1/2x ⊥ v(x) ∈ ℤ[x].

Definition. Let F be a field. Given two polynomials of F, say f(x), g(x) ∈ F[x], we say a monic polynomial d(x) (the coefficient of the leader term is equal to one) is the greatest common divisor of f and g, and we write it as d(x) = gcd(f(x), g(x)), if d(x)|f(x) and d(x)|g(x) and if ∃c(x) ∈ F[x] such that c(x)|f(x) and c(x)|g(x), then c(x)|d(x).

Definition. Let F be a field, two polynomials of F, say f(x), g(x) ∈ F[x]. If gcd(f(x), g(x)) = 1, then we say that both polynomials f and g are relatively prime.

Recall Bézout’s identity. Let a and b be integers with greatest common divisor d. Then there exist integers x and y such that ax + by = d. The following theorem shows that if F is a field, F[x] behaves quite a lot like ℤ.

Theorem. Given two polynomials of a non-empty field F, say f(x), g(x) ∈ F[x] with greatest common divisor d(x), d(x) = gcd(f(x), g(x)). Then, there exist two polynomials a(x), b(x) ∈ F[x] such that d(x) = a(x)f(x) + b(x)g(x).

Proof.

Consider S = {u(x)f(x) + v(x)g(x)| u(x), v(x)∈ F[x]} ≠ ∅ (e.g. u(x) = 1, v(x) = 0, ∀f(x) ∈ F[x], f(x) ∈ S and F is a non-empty field) and since the degrees of the elements in S are natural numbers (well-ordered), take d(x) ∈ S the monic polynomial of minimal degree ⇒ ∃a(x), b(x) ∈ F[x]: d(x) = a(x)f(x) + b(x)g(x).

1st Claim: d(x)|f(x).

By the division algorithm, f(x) = q(x)d(x) + r(x) where either r(x) = 0 or deg(r(x)) < deg(d(x)).

r(x) = f(x) -q(x)d(x) =[d(x) = a(x)f(x) + b(x)g(x)] f(x) -q(x)(a(x)f(x) + b(x)g(x)) = (1 -a(x)q(x))f(x) -q(x)b(x)g(x) ∈ S we only need to rename (1 -a(x)q(x)) = u(x), -q(x)b(x) = v(x) ⇒[By assumption, d(x) is the monic polynomial of minimal degree in S] r(x) = 0 ⇒ f(x) = q(x)d(x) ⇒ d(x)|f(x). Mutatis mutandis, d(x)|g(x).

2nd Claim: d(x) = gcd(f(x), g(x))

Suppose there exist c(x) ∈ F[x] such that c(x)|f(x) and c(x)|g(x) ⇒∃p(x), q(x) ∈ F[x], f(x) = c(x)p(x) and g(x) = c(x)q(x) ⇒ d(x) = a(x)f(x) + b(x)g(x) = a(x)c(x)p(x) + b(x)c(x)q(x) = c(x)(a(x)p(x) + b(x)q(x)) ⇒ d(x) = c(x)(a(x)p(x) + b(x)q(x)) ⇒ d(x)|c(x) ⇒ d(x) = gcd(f(x), g(x)).

3rc Claim: the gcd is unique.

Suppose d’(x) is also a greatest common divisor of f(x) and g(x) ⇒ d’(x)|f(x) and d’(x)|g(x) ⇒ ∃p(x), q(x) ∈ F[x]: f(x) = d’(x)p(x) and g(x) = d’(x)q(x) ⇒ d(x) = a(x)f(x) + b(x)g(x) = a(x)(d’(x)p(x)) + b(x)(d’(x)q(x)) = d’(x)(a(x)p(x) + b(x)q(x)) ⇒ d(x) = d’(x)(a(x)p(x) + b(x)q(x)) ⇒ deg(d(x)) = deg(d’(x)) + deg(a(x)p(x) + b(x)q(x)) ⇒[🚀deg(d(x)) = deg(d’(x))] deg(a(x)p(x) + b(x)q(x)) = 0 ⇒ a(x)p(x) + b(x)q(x) = α, α ∈ F, and d(x) = αd’(x) and d and d’ are monic polynomials ⇒ By considering the leader term, 1 = α ⇒ d(x) = d’(x)∎

🚀d(x)|f(x) and d(x)|g(x) ⇒[d’(x) = gcd(f(x), g(x))] d(x)|d’(x). Similarly, d’(x)|f(x) and d’(x)|g(x) ⇒[d(x) = gcd(f(x), g(x))] d’(x)|d(x) ⇒ d(x)|d’(x) and d’(x)|d(x) ⇒ deg(d(x)) = deg(d’(x))

• Example. f(x) = x² +2x +3 and g(x) = x² + 1. The reader could check that
  (x² +2x + 3) = (x² +1)·(1) + (2x + 2) ⇒ f(x) -g(x) = 2x +2
  (x² + 1) = (2x +2)(1/2·x -1/2) +2 ⇒ g(x) = (f(x)-g(x))(1/2·x -1/2) +2 ⇒ (-1/2·x +1/2)f(x) + (1/2·x+1/2·g(x)) = 2 ⇒ (-1/4·x +1/4)f(x) + (1/4·x+1/4·g(x)) = 1 = gcd(f(x), g(x)), and therefore they are relatively prime polynomials.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.