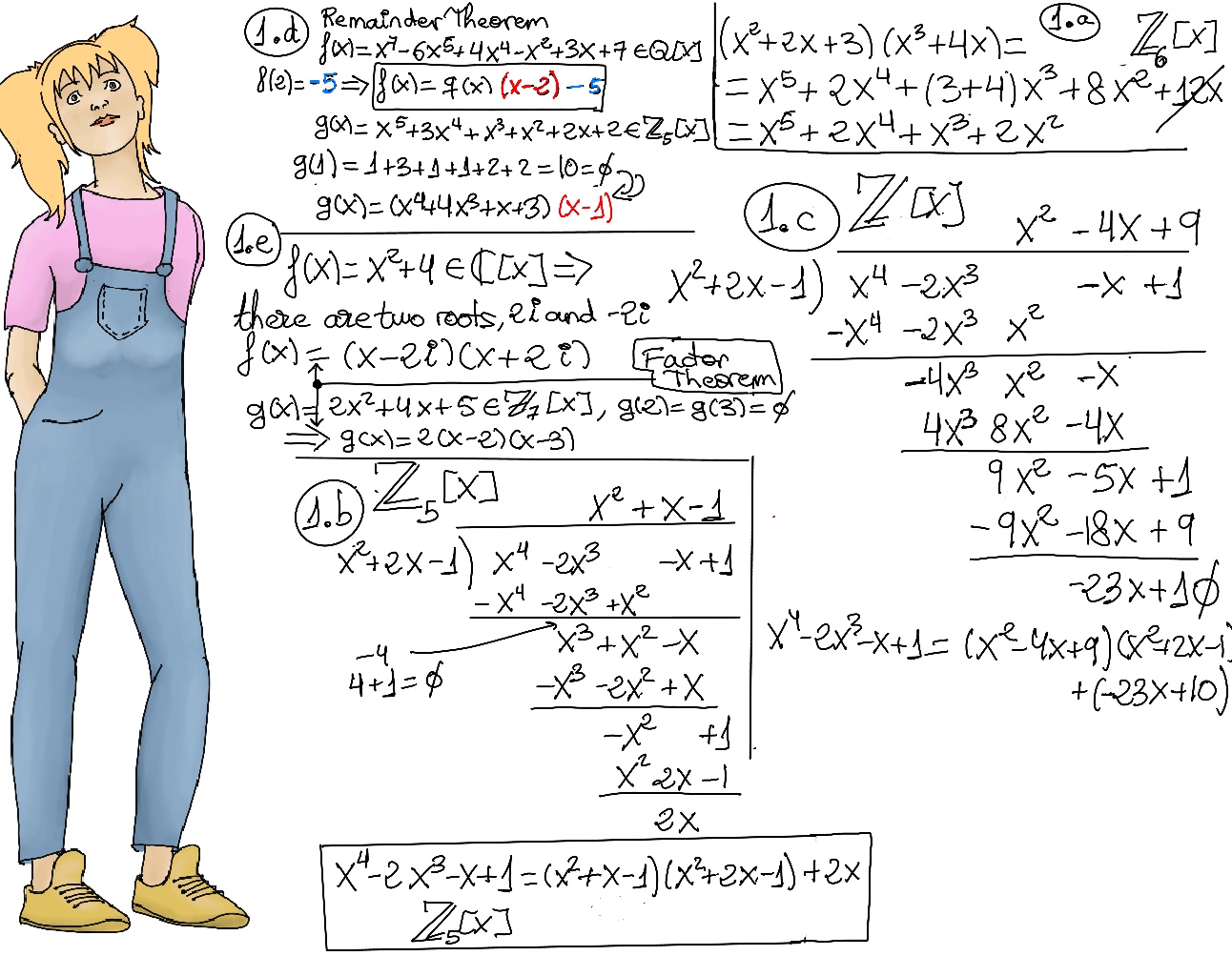Polynomial Rings. Division Algorithm.

“I hope you rot in the deepest, darkest, and filthiest pit of hell where you really belong, being tormented day and night watching CNN, MSNBC, and woke movies and series forever,” Apocalypse, Anawim, #justtothepoint.

Recall. A commutative ring is a ring in which the multiplication operation is commutative,i.e., ∀a, b ∈ R, a·b = b·a.

Definition. Let R be a commutative ring. A polynomial ring is a ring formed from the set of polynomials in one or more indeterminates or variables with coefficients in R. R[x] = {a_nxⁿ + a_n-1x^n-1+ ··· + a₁x + a₀ | a_i ∈ R, n ∈ ℤ⁺}, e.g. 2x³+ 7x² +4∈ ℤ[x], ²⁄₃x² + 4x -7 ∈ ℚ[x].

The degree of f(x) = a_nxⁿ + a_n-1x^n-1+ ··· + a₁x + a₀, expressed or written as deg(f(x)), is the largest k such that the coefficient of a_k is not zero. If a_n ≠ 0, we say that f(x) has degree n and its leading coefficient is a_n. A constant polynomial is either the zero polynomial or a polynomial of degree zero.

Two polynomials a_nxⁿ + a_n-1x^n-1+ ··· + a₁x + a₀ and b_mx^m + b_m-1x^m-1+ ··· + b₁x + b₀ are equal when the corresponding coefficients of x^k are equal, a_i = b_i ∀i ∈ ℤ⁺, a_i = 0 when m < i ≤ n, b_j = 0 when n < j ≤ m

Let R be a commutative ring, and let f(x) = a_nxⁿ + a_n-1x^n-1+ ··· + a₁x + a₀ and g(x) = b_mx^m + b_m-1x^m-1+ ··· + b₁x + b₀ ∈ R[x]. The polynomial ring R[x] is equipped with addition and multiplication,

1. f(x) + g(x) = $\sum_{i=0}^{max(m,n)} (a_i+b_i)x^i$ = (a_s + b_s)x^s + (a_s-1 + b_s-1)x^s-1+ ··· + (a₁ + b₁)x + a₀ + b₀, where s = max(m, n), a_i = 0 for i > n, b_i = 0 for i > m.
2. f(x)g(x) = = $\sum_{k=0}^{m + n} (\sum_{i=0}^k a_ib_{k-i})x^k$ = c_m+nx^m+n + c_m+n-1x^m+n-1+ ··· + c₁x + c₀ where c_k = a_kb₀ + a_k-1b₁ + ··· + a₁b_k-1 + a₀b_k, for k = 0,···, m+n

Examples

• f(x) = x² − 5x + 6 ∈ ℤ[x] and g(x) = 2x³ − 5 ∈ ℤ[x], f(x) + g(x) = 2x³ + x² − 5x + 1, and f(x)g(x) = 2x⁵ − 10x⁴ + 12x³ − 5x² + 25x − 30.
• f(x) = 2x³ + x² + 2x + 2, g(x) = 2x² + 2x + 1 ∈ ℤ₃[x], then f(x) + g(x)=[2x³ + 3x² + 4x + 3] 2x³ + x because addition and multiplication of the coefficients are done modulo 3. f(x)·g(x) = x⁵ + 2x³ + 2.

  $(2x^3+x^2+2x+2)(2x^2+2x+1) = 4x^5+(4+2)x^4+(2+2+4)x^3+(1+4+4)x^2+(2+4)x+2=x^5+2x^3+2$

• (x² + 2x + 3)(x³ + 4x) = x⁵ + 2x⁴ + x³ + 2x² in ℤ₆[x] (Figure 1.a.)  

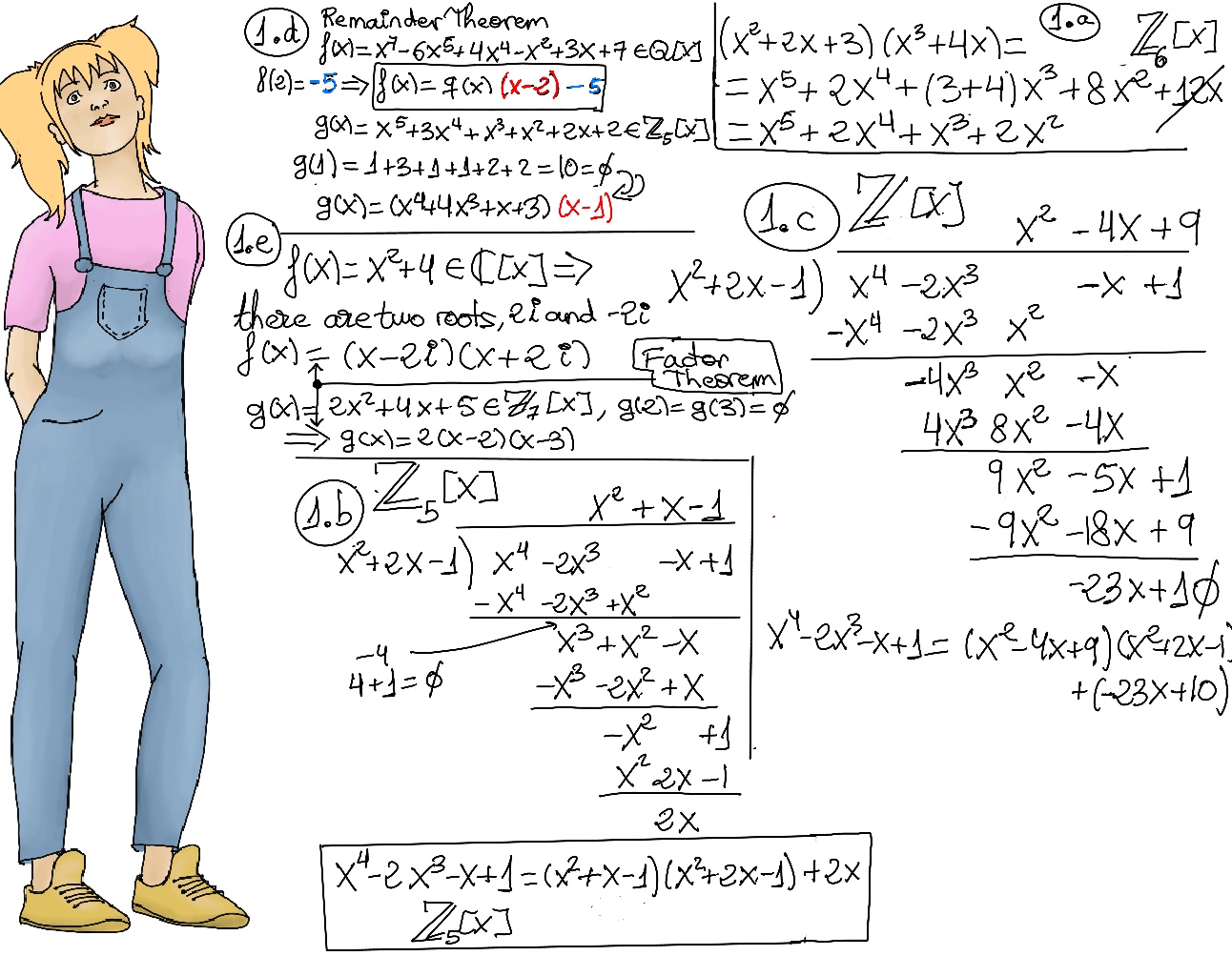
Theorem. Let R be a commutative ring with unity 1. R[x] is a commutative ring under the operations of polynomial addition and multiplication with unity (1, 0, 0, ···).

Proof.

It is left to the reader to verify that (R[x], +, ·) is a commutative ring with unity (1, 0, 0, · · ·). Besides, (0, 0, · · ·) is the zero element of R[x] and the addition inverse of (a₀, a₁, ···, a_n) is (-a₀, -a₁, ···, -a_n).

Futhermore, the mapping a → (a, 0, 0, ···) is a monomorphism (an injective homomorphism) of the ring R into R[x]. Thus (R ≋ Φ(R[x])), R can be considered as a subring of R[x] and we no longer need to distinguish between a and (a, 0, 0, ···).

Theorem. Let D be a commutative ring with unity 1. Then, D[x] is an integral domain if and only if D is an integral domain.

Proof.

Recall that an integral domain is a commutative ring with unity in which the product of any two nonzero elements is nonzero.

⇒ ) Suppose D[x] is an integral domain. D is a subring of D[x] (D ⊆ D[x]), then it is obvious that D must also be commutative ring with unity(🚀) and has no zero divisors (∀x, y ∈ D with x·y = 0, x, y ∈ D[x] ⇒[D[x] is an integral domain] x = 0 or y = 0).

🚀 Consider the map, Φ:R[x] → R, such that Φ(f(x)) = Φ(a₀ + a₁x + ··· + a_nx_n) = a₀. Φ is an onto homomorphism (it is left as an easy exercise) ⇒ R is a homomorphic image of R[x], a ring with unity and [A homomorphic image of a ring with unity is a ring with unity] Φ(e(x)) will be the unity of R where e(x) is the unity of R[x].

⇐ ) Conversely, suppose D be an integral domain.

1. We already know that D[x] is a ring.
2. D is a commutative ring ⇒ D[x] is a commutative ring, too.
3. Futhermore, f(x) = 1 is the unity element.
4. Let’s prove that D[x] has no zero-divisors. Suppose that f(x) = a_nxⁿ + a_n-1x^n-1+ ··· + a₁x + a₀ and g(x) = b_mx^m + b_m-1x^m-1+ ··· + b₁x + b₀ ∈ D[x] are non-zero polynomials, that is, a_n ≠ 0, b_m ≠ 0 for some n and m positive integers.

f(x)·g(x) = c_m+nx^m+n + c_m+n-1x^m+n-1+ ··· + c₁x + c₀ where c_k = a_kb₀ + a_k-1b₁ + ··· + a₁b_k-1 + a₀b_k, for k = 0,···, m+n

Its leading coefficient is c_m+n = a_nb_m ≠ 0 because D is an integral domain. Therefore, f(x) ≠ 0 and g(x) ≠ 0 ⇒ f(x)·g(x) ≠ 0, hence D[x] has no zero-divisors.

Theorem. Let R be an integral domain, let f and g be two nonzero polynomials in R[x], then deg(fg) = deg(f) + deg(g).

Proof:

Suppose f(x) = a_nxⁿ + a_n-1x^n-1+ ··· + a₁x + a₀ and g(x) = b_mx^m + b_m-1x^m-1+ ··· + b₁x + b₀ are nonzero polynomials of degree n and m respectively, i.e., a_n, b_m ≠ 0_R ⇒ the highest possible degree of fg is n + m and the coefficient of x^n+m is a_nb_m.

Since R is an integral domain, a_nb_m = 0_R if and only if a_n = 0_R or b_m = 0_R. Therefore, a_n, b_m ≠ 0_R ⇒ a_n·b_m ≠ 0_R ⇒ deg(fg) = n + m = deg(f) + deg(g).

Theorem. Let R be an integral domain, then the units of R[x] are the units of R.

Proof:

Suppose f(x) = a_nxⁿ + a_n-1x^n-1+ ··· + a₁x + a₀ is a unit ⇒ there exist g(x) ∈ R[x], say deg(f(x)) = n, and deg(g(x)) = m, such that f(x)·g(x) = 1 ⇒[deg(fg) = deg(f) + deg(g), f(x)·g(x) = 1] n + m = 0 ⇒ n = m = 0 ⇒ f(x) = u ∈ R, g(x) = v ∈ R, u·v = 1, and therefore u and v are units in R.

Theorem. If I is an ideal of a ring R, define I[x] = {i₀ +i₁x +··· + i_nxⁿ| i_j∈ I}. Then, R[x]/I[x] ≋ (R/I)[x]

Proof.

Consider Φ: R[x] → (R/I)[x] given by Φ(a₀ +a₁x +··· + a_nxⁿ) = (a₀ + I) +(a₁ + I)x +··· + (a_n + I)xⁿ

Φ is a surjective homomorphism.

∀f(x), g(x) ∈ R[x], f(x) = a_nxⁿ + a_n-1x^n-1+ ··· + a₁x + a₀ and g(x) = b_mx^m + b_m-1x^m-1+ ··· + b₁x + b₀

Φ(f(x) + g(x)) = Φ($\sum_{i=0}^{max(m,n)} (a_i+b_i)x^i$) = $\sum_{i=0}^{max(m,n)} (a_i+b_i+I)x^i$ =[By the definion of coset addition] $\sum_{i=0}^{max(m,n)} (a_i+I)x^i+\sum_{i=0}^{max(m,n)} (b_i+I)x^i$ = Φ(f(x)) + Φ(g(x))

Similarly, Φ(f(x) · g(x)) = Φ(f(x))·Φ(g(x)). Futhermore, Φ is onto. Let F[x] ∈ (R/I)[x], then F[x] = $\bar a_0 + \bar a_1x + ··· + \bar a_nx^n,\bar a_0 = a_0 + I, \bar a_1 = a_1 + I, ···, \bar a_n = a_n + I, a_0, a_1, ···, a_n ∈ R$. Set f(x) = a₀ + a₁x + ··· + a_nxⁿ ∈ R[x], and obviously Φ(f(x)) = F[x] and F[x] was taken an arbitrary element of (R/I)[x].

f(x) = a₀ + a₁x + ··· + a_nxⁿ ∈ Ker(Φ) ↭ a_k + I = 0 + I ∀0 ≤ k ≤ n ↭ a_k ∈ I ∀0 ≤ k ≤ n ↭ f(x) ∈ I[x], hence ker(Φ) = I[x]. Finally, by the First Isomorphism Theorem for rings, R[x]/I[x] ≋ (R/I)[x]

Theorem. P ⊆ R is a prime ideal if and only if P[x] ⊆ R[x] is a prime ideal.

Proof.

Recall: A prime ideal A of a commutative ring R is a proper ideal of R such that if a, b are two elements of R, and whenever their product ab is an element of A, then either a is in A, b is in A or both, i.e., a, b ∈ R, ab ∈ A ⇒ a ∈ A or b ∈ A. Example: ⟨x⟩ ⊆ ℤ[x] is a prime ideal, but ⟨x²⟩ is not, because x² ∈ ⟨x²⟩ but x ∉ ⟨x²⟩.

P ⊆ R is a prime ideal ↭[Theorem. Let R be a commutative ring with unity, and let A be an ideal of R. Then, A is a prime ideal iff R/A is an integral domain.] R/P is an integral domain ↭[Theorem. Let D be a commutative ring with unity 1. Then, D[x] is an integral domain if and only if D is an integral domain.] (R/P)[x] is an integral domain ↭[Theorem. If I is an ideal of a ring R, define I[x] = {i₀ +i₁x +··· + i_nxⁿ| i_j∈ I}. Then, R[x]/I[x] ≋ (R/I)[x]] R[x]/P[x] is an integral domain ↭ P[x] is a prime ideal ∎

Division Algorithm. Let F be a field, f(x), g(x) ∈ F[x], g(x) ≠ 0. Then, there exists unique polynomials q(x) and r(x) ∈ F[x] such that

1. f(x) = g(x)q(x) + r(x)
2. Either r(x) = 0 or deg(r(x)) < deg(g(x)).

Proof.

We first prove the existence of the polynomials q and r. There are three possibilities:

1. Suppose f = 0, then the proposition is true with q = r = 0_F[x] (q(x) = r(x) = 0).
2. Suppose deg(f) < deg(g), then the proposition is true with q = 0_F[x] and r = f.
3. Suppose deg(f) ≥ deg(g), then the proof of existence is obtained by induction on the degree of f.

3.1 If deg(f) = 0 ⇒ deg(g) = 0 ⇒ f = a, g = b, for some nonzero elements a and b, a, b ∈ F ⇒ [F is a field, and by assumption, b = g(x) ≠ 0, and therefore b is a unit, ∃b^-1: bb^-1 = b^-1b = 1] f = a = b(b^-1a) = g(b^-1a), the theorem holds with q = b^-1a, and r = 0_F

3.2 Let’s assume that the proposition holds whenever deg(f) < n. We must show that it is true when f(x) has degree n, say f(x) = a_nxⁿ + a_n-1x^n-1+ ··· + a₁x + a₀ with a_n ≠ 0_F. The divisor g(x) = b_mx^m + b_m-1x^m-1+ ··· + b₁x + b₀, b_m ≠ 0_F, and m ≤ n.

b_m ≠ 0 (By assumption, g(x) ≠ 0), F is a field ⇒ b_m is an unit. Next, we multiply the divisor g by a_nb_m^-1x^n-m (n -m ≥ 0) to obtain (a_nb_m^-1x^n-m·g) = a_nxⁿ + a_nb_m^-1b_m-1x^n-1 + ··· + a_nb_m^-1b₀x^n-m

Since the leading term of this polynomial is identical to that of f, namely a_n, the difference of f - a_nb_m^-1x^n-m·g is a polynomial of degree less than n, and we can apply the induction hypothesis with g as the divisor polynomial and f - a_nb_m^-1x^n-m·g as the dividend ⇒ ∃ polynomials q₁ and r:

f - a_nb_m^-1x^n-m·g = q₁g + r, r = 0_F or deg(r) < deg(g).

f = (a_nb_m^-1x^n-m + q₁)·g + r, r = 0_F or deg(r) < deg(g) ∎

To prove that q and r are unique, suppose that q’ and r’ are polynomials satisfying f = q’g + r’, r’ = 0_F and deg(r’) < deg(g).

qg + r = f = q’g + r’ ⇒ g(q - q’) = r’ - r.

If q - q’ ≠ 0_F ⇒ the degree of the polynomial on the right hand size of the last equation (r’ - r) is greater than or equal to the degree of g [deg(r’-r) ≥ deg(g) + deg(q -q’) ⇒ deg(r’-r) ≥ deg(g)]. But this is not possible since the polynomials r’ and r are either zero or have degree strictly less that of g ⇒ q’ = q ⇒[By assumption, g(x) ≠ 0] r’ = r ∎

Example: x⁴ -2x³ -x +1 = (x² + x -1)(x² +2x -1) + 2x in ℤ₅[x] (Figure 1.b.). x⁴ -2x³ -x +1 = (x² - 4x +9)(x² +2x -1) + (-23x + 10) in ℤ (Figure 1.c.)  

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.