Integration by parts II

Winners never quit and quitters never win. Football is like life - it requires perseverance, self-denial, hard work, sacrifice, dedication and respect for authority, Vince Lombardi.

Recall

Antiderivatives are fundamental concepts in calculus. They are the inverse operation of derivatives.

Given a function f(x), an antiderivative, also known as indefinite integral, F, is the function that can be differentiated to obtain the original function, that is, F’ = f, e.g., 3x² -1 is the antiderivative of x³ -x +7 because $\frac{d}{dx} (x^3-x+7) = 3x^2 -1$. Symbolically, we write F(x) = $\int f(x)dx$.

The process of finding antiderivatives is called integration.

The Fundamental Theorem of Calculus states roughly that the integral of a function f over an interval is equal to the change of any antiderivate F (F'(x) = f(x)) between the ends of the interval, i.e., $\int_{a}^{b} f(x)dx = F(b)-F(a)=F(x) \bigg|_{a}^{b}$

Integration by parts

It is a technique used in calculus to evaluate integrals of the form $\int uv’dx$. Recall that (uv)’ = u’v + uv’ ⇒ uv’ = (uv)’ -u’v ⇒ $\int uv’dx = uv -\int u’vdx$, e.g., $\int lnx dx =$[u = lnx, u’ = 1/x, v = x, v’ = 1] xlnx -$\int \frac{1}{x}xdx = xlnx -x + C.$ 🚀

Solved exercises

• $\int \frac{ln(x)}{x^2}dx$ =[Integration by parts, ∫udv = uv - ∫vdu. u = ln(x), v’ =1/x², u’ = dx/x, v =-1/x] $ln(x)·\frac{-1}{x}-\int \frac{dx}{x}\frac{-1}{x} = \frac{-ln(x)}{x}+\int \frac{dx}{x^2} = \frac{-ln(x)}{x} -\frac{1}{x} + C = -\frac{ln(x)+1}{x}+C.$

• $\int xsec^2(x)dx =$ [Integration by parts, ∫udv = uv - ∫vdu. u = x, v’ = sec²(x)dx, u’ = dx, v = tan(x). Integration formulas for trigonometry] x·tan(x) - $\int tan(x)dx = xtan(x) -(-ln(|cos(x)|)) + C = xtan(x) +ln|cos(x)| + C.$

• $\int e^xsin(x)dx$ =[Integration by parts, ∫udv = uv - ∫vdu. u = sin(x), v’=e^xdx, u’ = cos(x)dx, v = e^x] $e^xsin(x)-\int e^xcos(x)dx$ =[u = cos(x), v’ = e^xdx, u’ = -sin(x)dx, v = e^x] $e^xsin(x)-(e^xcos(x)-\int e^x(-sin(x))) ⇒ \int e^xsin(x)dx = e^xsin(x)-e^xcos(x)-\int e^xsin(x) ⇒ 2\int e^xsin(x)dx = e^xsin(x)-e^xcos(x) ⇒ \int e^xsin(x)dx = \frac{1}{2}e^x(sin(x)-cos(x)) + C.$

• $\int_{1}^{4} x^{\frac{1}{2}}ln(2x)dx$ =[Integration by parts, ∫udv = uv - ∫vdu. u = ln(2x), v’=x^1/2dx, du = ²⁄_2xdx = ¹⁄_x, v = ²⁄₃x^3⁄₂] $\frac{2}{3}x^{\frac{3}{2}}ln(2x) -\int_{1}^{4} \frac{2}{3}x^{\frac{3}{2}}·\frac{1}{x}dx = \frac{2}{3}x^{\frac{3}{2}}ln(2x) -\frac{2}{3}\int_{1}^{4} x^{\frac{1}{2}}dx =\frac{2}{3}x^{\frac{3}{2}}ln(2x) -\frac{2}{3}\frac{2}{3}x^{\frac{3}{2}} = \frac{2}{3}x^{\frac{3}{2}}ln(2x) -\frac{4}{9}x^{\frac{3}{2}}\bigg|_{1}^{4} = (\frac{2}{3}8ln(8) -\frac{32}{9})-(\frac{2}{3}ln(2) -\frac{4}{9}) = (\frac{2}{3}8ln(2^3) -\frac{32}{9})-(\frac{2}{3}ln(2) -\frac{4}{9}) = (16ln(2) -\frac{32}{9})-(\frac{2}{3}ln(2) -\frac{4}{9}) = 16ln(2) -\frac{32}{9}-\frac{2}{3}ln(2)+\frac{4}{9} = \frac{46}{3}ln(2)-\frac{28}{9} ≈ 7.51$

• $\int arcsin(x)dx$ =[Integration by parts, ∫udv = uv - ∫vdu. u = arcsin(x), v’ = dx, u’ = $\frac{1}{\sqrt{1-x^2}}dx$, v = x] $x·arcsin(x)-\int \frac{x}{\sqrt{1-x^2}}dx$ =[U-substitution, u = 1 -x², du = -2xdx] $x·arcsin(x)+\frac{1}{2}\int \frac{1}{\sqrt{u}}dx = x·arcsin(x)+\frac{1}{2}2\sqrt{u} = x·arcsin(x)+\sqrt{u} = x·arcsin(x)+\sqrt{1-x^2}+C.$

• Find the volume of an exponential wineglass, that is, y = e^x rotated around the y-axis between y = 1 and y = e.

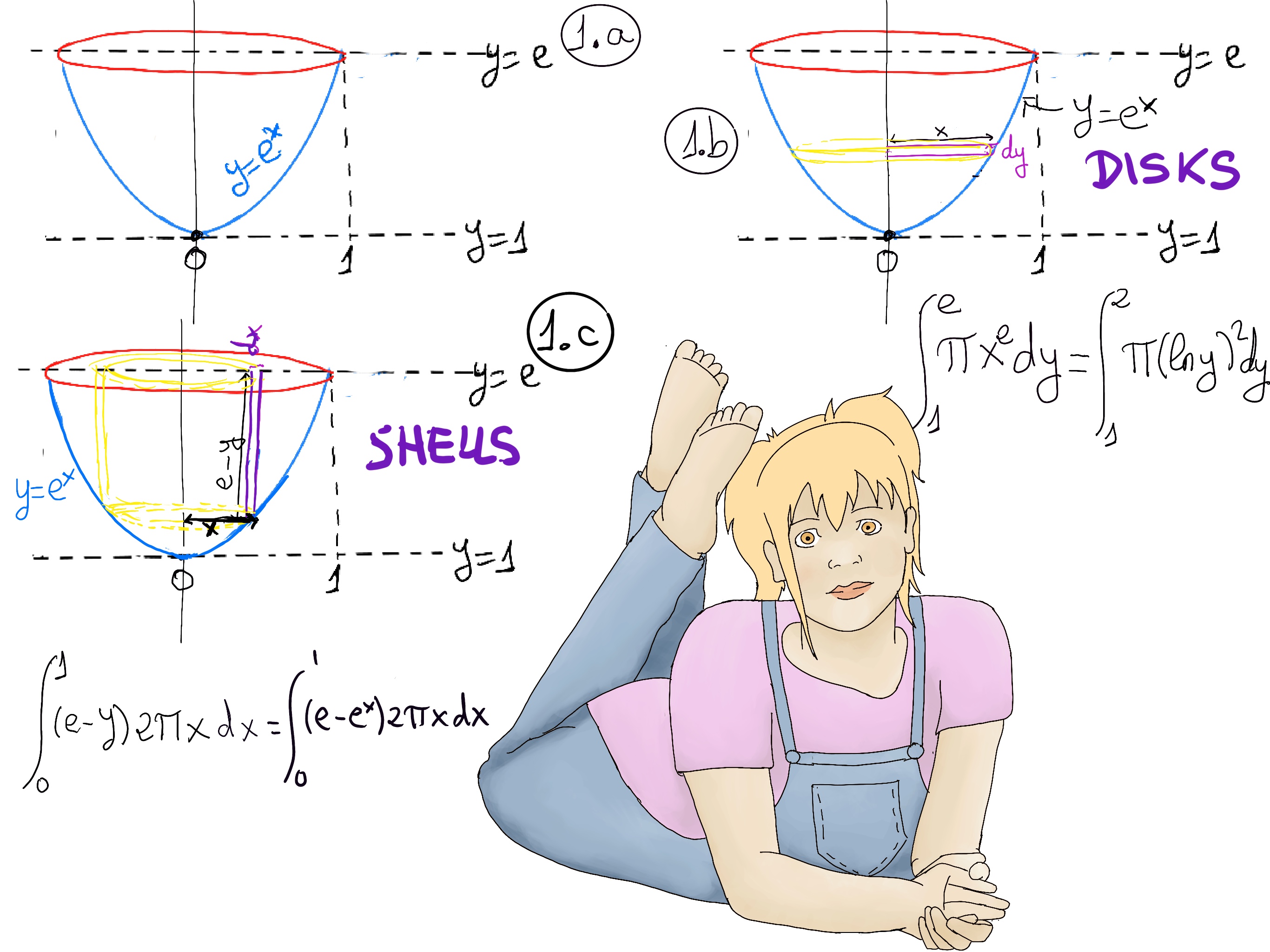
The obvious answer is -horizontal slicing- $\int_{1}^{e} πx^2dy$ =[y = e^x, x = lny] π$\int_{1}^{e} (lny)^2dy = πF_2(y)\bigg|_{1}^{e}$ =

Considering a previous exercise = $π(y(lny)^2-2(ylny -y)) \bigg|_{1}^{e} = π(e·1^2)- 2π(e·1-e) -π(1·0^2-2(1·0-1))= πe -0 -2π= π(e-2)$.

Analogously, the answer is -vertical slicing- $\int_{0}^{1} (e-y)2πxdx = \int_{0}^{1} (e-e^x)2πxdx = \int_{0}^{1}2πexdx -2π\int_{0}^{1} xe^xdx $=[A previous exercise]$ 2πe\frac{x^2}{2} -2πxe^x +2πe^x\bigg|_{0}^{1} = 2πe\frac{1}{2}-2πe+2πe-2π = πe -2π = π(e-2).$

• $\int xtan^{-1}(x)dx$ =[v’=xdx, u = tan^-1x, u’ = ¹⁄_1+x², v = x²/2] = $\frac{x^2}{2}tan^{-1}(x) - \int \frac{x^2}{2}\frac{1}{1+x^2}dx = \frac{x^2}{2}tan^{-1}(x) - \frac{1}{2}\int \frac{x^2}{1+x^2}dx$ = [^x²⁄_1+x² = ^x²+1-1⁄_1+x² = 1-¹⁄_1+x² ] = $\frac{x^2}{2}tan^{-1}(x)-\frac{1}{2}x+\frac{1}{2}tan^{-1}x + C.$

• $\int x^3ln(x)dx =$[u = ln(x), v’= x³dx, u’ = ¹⁄_xdx, v = ^x4⁄₄] $ln(x)\frac{x^4}{4}-\int \frac{x^4}{4}\frac{1}{x}dx = ln(x)\frac{x^4}{4}-\frac{1}{4}\int x^3dx = ln(x)\frac{x^4}{4}-\frac{1}{4}\frac{x^4}{4}+C = \frac{1}{4}(x^4ln(x)-\frac{x^4}{4})+C.$

• Prove that $\int_{0}^{∞} x^ne^{-x}dx = n!$ for all n ≥ 0.

Case base, n = 0, $\int_{0}^{∞} x^ne^{-x}dx = \int_{0}^{∞} e^{-x}dx = \lim_{t \to ∞} -e^{-x}\bigg|_{0}^{t} =$

$\lim_{t \to ∞} (-\frac{1}{e^t}+1) = 1 = 0!.$

Induction hypothesis, for k ≥ 0, the equality holds, $\int_{0}^{∞} x^ke^{-x}dx = k!$

Let’s consider $\int_{0}^{∞} x^{k+1}e^{-x}dx$ =[u = x^k+1, du = (k+1)x^kdx, dv = e^-xdx, v = -e^-x] = [1] + [2]

[1] $-x^{k+1}e^{-x}\bigg|_{0}^{∞} = 0 -0 = 0$. And the key is to understand that the exponent term e^-x goes to zero much faster than any power of x grows to infinity.

Another way of seeing it, $\lim_{x \to ∞} \frac{x^k}{e^{x}} =$[L’Hôpital’s rule] $\lim_{x \to ∞} \frac{kx^{k-1}}{e^{x}} = \lim_{x \to ∞} \frac{k(k-1)x^{k-2}}{e^{x}} = ··· = \lim_{x \to ∞} \frac{some~constant}{e^{x}} = 0$

[2] $+ (k+1)\int_{0}^{∞} x^ke^{-x}dx = $[Induction hypothesis, for k ≥ 0, the equality holds, $\int_{0}^{∞} x^ke^{-x}dx = k!$] (k+1)k! = (k+1)!, hence $\int_{0}^{∞} x^ne^{-x}dx = n!$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.