Integration of Trigonometric Functions

Beneath this mask there is more than flesh. Beneath this mask there is an idea, Mr. Creedy, and ideas are bulletproof, V for Vendetta.

Recall

In calculus, an antiderivative or indefinite integral, G, of a function g, is the function that can be differentiated to obtain the original function, that is, G’ = f.

G(x) = $\int f(x)dx$

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles.

Here are some of the main important trigonometric definitions and formulas:

• Functions of Right Triangles. $\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}, \cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}}, \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}, \cot(\theta) = \frac{1}{\tan(\theta)}, \sec(\theta) = \frac{1}{\cos(\theta)}, \csc(\theta) = \frac{1}{\sin(\theta)}$

• Pythagorean Identities: $\sin^2(θ) + \cos^2(θ) = 1, 1 + \tan^2(θ) = \sec^2(θ), 1 + \cot^2(θ) = \csc^2(x)$

• Complementary angles: $\sin\left(\frac{\pi}{2} - x\right) = \cos(x), \cos\left(\frac{\pi}{2} - x\right) = \sin(x), \tan\left(\frac{\pi}{2} - x\right) = \cot(x), \cot\left(\frac{\pi}{2} - x\right) = \tan(x), \sec\left(\frac{\pi}{2} - x\right) = \csc(x), \csc\left(\frac{\pi}{2} - x\right) = \sec(x).$

• Addition and Subtraction Formulas: $\sin(x \pm y) = \sin(x)\cos(y) \pm \cos(x)\sin(y), \cos(x \pm y) = \cos(x)\cos(y) \mp \sin(x)\sin(y), \tan(x \pm y) = \frac{\tan(x) \pm \tan(y)}{1 \mp \tan(x)\tan(y)}.$

• Double Angle Formulas: $\sin(2θ) = 2\sin(θ)\cos(θ), \cos(2θ) = \cos^2(θ) - \sin^2(θ) = 2\cos^2(θ) - 1 = 1 - 2\sin^2(θ), tan(2θ) = \frac{2\tan(θ)}{1 - \tan^2(θ)}.$

cos(2θ) = cos²(θ) -sin²(θ) =[sin²(θ) + cos²(θ) = 1] cos²(θ) -(1 - cos²(θ)) = 2cos²(θ) -1 ⇒ cos²(θ) = ^{(1 + cos(2θ))}⁄₂. Similarly, sin²(θ) = ^{(1 - cos(2θ))}⁄₂.

• Half-Angle Formulas: $\sin^2\left(\frac{θ}{2}\right) = \frac{1 - \cos(θ)}{2} ↭ \sin(\frac{θ}{2}) = ±\sqrt{\frac{1 - \cos(θ)}{2}}, \cos^2\left(\frac{θ}{2}\right) = \frac{1 + \cos(θ)}{2} ↭ \cos(\frac{θ}{2}) = ±\sqrt{\frac{1 + \cos(θ)}{2}}, \tan\left(\frac{θ}{2}\right) = \frac{1 - \cos(θ)}{\sin(θ)} = \frac{\sin(θ)}{1 + \cos(θ)}.$

• Derivatives of Trigonometric Formulas: sin’(x) = cos(x), cos’(x) = -sin(x), tan’(x) = sec²(x), sec’(x) = sec(x)tan(x), $\csc’(x) = -\csc(x) \cot(x), \cot’(x) = -\csc^2(x)$.

• Integration formulas for trigonometry: $\int \sin(x)dx = -\cos(x) + C; \int \cos(x)dx = \sin(x) + C; \int \tan(x)dx = -\ln|\cos(x)| + C; \int \cot(x)dx = \ln|\sin(x)| + C; \int \sec(x)dx = \ln|\sec(x) + \tan(x)| + C; \int \csc(x)dx = -\ln|\csc(x) + \cot(x)| + C, \int sec(x)tan(x)dθ = sec(x) + C$

sec²(x) = $\frac{1}{cos^2(x)} = \frac{cos^2(x)+sin^2(x)}{cos^2(x)} = 1 + tan^2(x)$. Similarly, $\frac{d}{dx}tan(x) = \frac{d}{dx}\frac{sin(x)}{cos(x)} = \frac{cos^2(x)+sin^2(x)}{cos^2(x)} = \frac{1}{cos^2(x)}=sec^2(x)$. Besides, $\frac{d}{dx} sec(x) = \frac{d}{dx} \frac{1}{cos(x)} = \frac{sin(x)}{cos^2(x)} = sec(x)tan(x).$

Trigonometry substitution for integrals.

Trigonometric substitution is a powerful technique used in calculus to simplify and solve integrals involving radical expressions.

1. Identify the form of the radical expression in the integral.
2. Choose a trigonometric function based on the form of the expression, e.g., if $\sqrt{a^2-x^2}$ is present consider using x = acos(θ) or x = asin(θ) to get asin(θ) or acos(θ) respectively. Similarly, if $\sqrt{a^2+x^2}$ is present, consider taking x = atan(θ) to get asec(θ) (Recall sec²(x) = 1 + tan²(x) ⇒ a²+x² = a²(1 + tan²(θ)) = a²sec²(θ)). Finally, if $\sqrt{x^2-a^2}$ is present consider using x = asec(θ), because x²-a² = a²sec²(θ) -a² = a²(sec²(θ)-1) = a²tan²(θ).
3. Substitute the chosen trigonometric function into the expression, expressing the indefinite variable x in terms of the trigonometric function.
4. Adjust the differential dx based on the chosen substitution, e.g., if x = asin(θ), dx = acos(θ)dθ.
5. Substitute and simplify the expression involving trigonometric functions and the adjusted differential into the original integral.
6. Integrate the simplified expression with respect to the new variable ($\theta$). After integration is completed, back-substitute the original variable x in terms of θ. Simplify the expression further, if necessary, and include any constants of integration.

Completing the square

It is another technique often used in calculus to simplify complex expressions to make integration more manageable.

1. Identify the “problematic” expression, e.g., if the integral is $\int \frac{dx}{\sqrt{x^2+4x}}$, the difficult expression would be x² + 4x.
2. If the coefficient of the quadratic term is not 1, factor it out, that is, divide every term by the coefficient of the quadratic term.
3. Complete the square, rewrite our expression as (x + a)² + c, e.g., x² + 4x = (x + 2)² -4.
4. Make the substitution, e.g., u = x +2, du = dx, so x² + 4x = (x + 2)² -4 = u² -4, and rewrite the integral, $\frac{du}{\sqrt{u^2-4}}$.
5. Simplify the integral, integrate, and back-substitute the original variable. In our case, we use trigonometric substitution, as it was previously mentioned, u = 2sec(θ), du = 2sec(θ)tan(θ)dθ. $\int \frac{du}{\sqrt{u^2-4}}$ =[$u^2-4 = 4sec^2(θ)-4=4(sec^2(θ)-1)=4tan^2(θ)$] $\int \frac{2sec(θ)tan(θ)dθ}{\sqrt{4tan^2(θ)}} = \int \frac{2sec(θ)tan(θ)dθ}{2tan(θ)} = \int sec(θ)dθ$ =[🚀] $ln|sec(θ)+tan(θ)| + C =$[$u=2sec(θ)⇒ sec(θ)=\frac{u}{2}, u^2-4 = 4tan^2(θ)⇒ tan^2(θ) = \frac{u^2-4}{4}$] $ln|\frac{u}{2}+\frac{\sqrt{u^2-4}}{2}| + C$ =[$u = x + 2$] $ln|\frac{x+2}{2}+\frac{\sqrt{x^2+4x}}{2}|+C.$

Exercises

• $\int tan(x)dx = \int \frac{sin(x)}{cos(x)}dx$ [Trigonometry substitution, u = cos(x), du = -sin(x)dx] =$\int \frac{-du}{u} = -ln|u| + C = -ln|cos(x)| + C.$

• $\int \sqrt{1-x^2}dx =$[Trigonometry substitution, x = sin(θ), dx = cos(θ)dθ] $\int \sqrt{1-sin^2(θ)}cos(θ)dθ = \int \sqrt{cos^2(θ)}cos(θ)dθ = \int cos^2(θ)dθ$ =[Double Angle Formulas, cos(2θ) = 2cos²(θ)-1 ⇒ $cos^2(θ) = \frac{1}{2}·(1+cos(2θ))$] $\frac{1}{2}\int (1+cos(2θ))dθ = \frac{1}{2}(θ+\frac{1}{2}sin(2θ))+C = \frac{1}{2}(θ+sin(θ)cos(θ))+C = \frac{1}{2}θ + \frac{1}{2}sin(θ)cos(θ)+C.$

Now, we need to backtrack our substitution (Figure 3), $x = sin(θ) ⇒ sin(θ)=\frac{x}{1} ⇒ θ = sin^{-1}(x), \int \sqrt{1-x^2}dx = \frac{1}{2}θ + \frac{1}{2}sin(θ)cos(θ)+C = \frac{1}{2}(sin^{-1}(x))+ \frac{1}{2}x\sqrt{1-x^2} + C.$

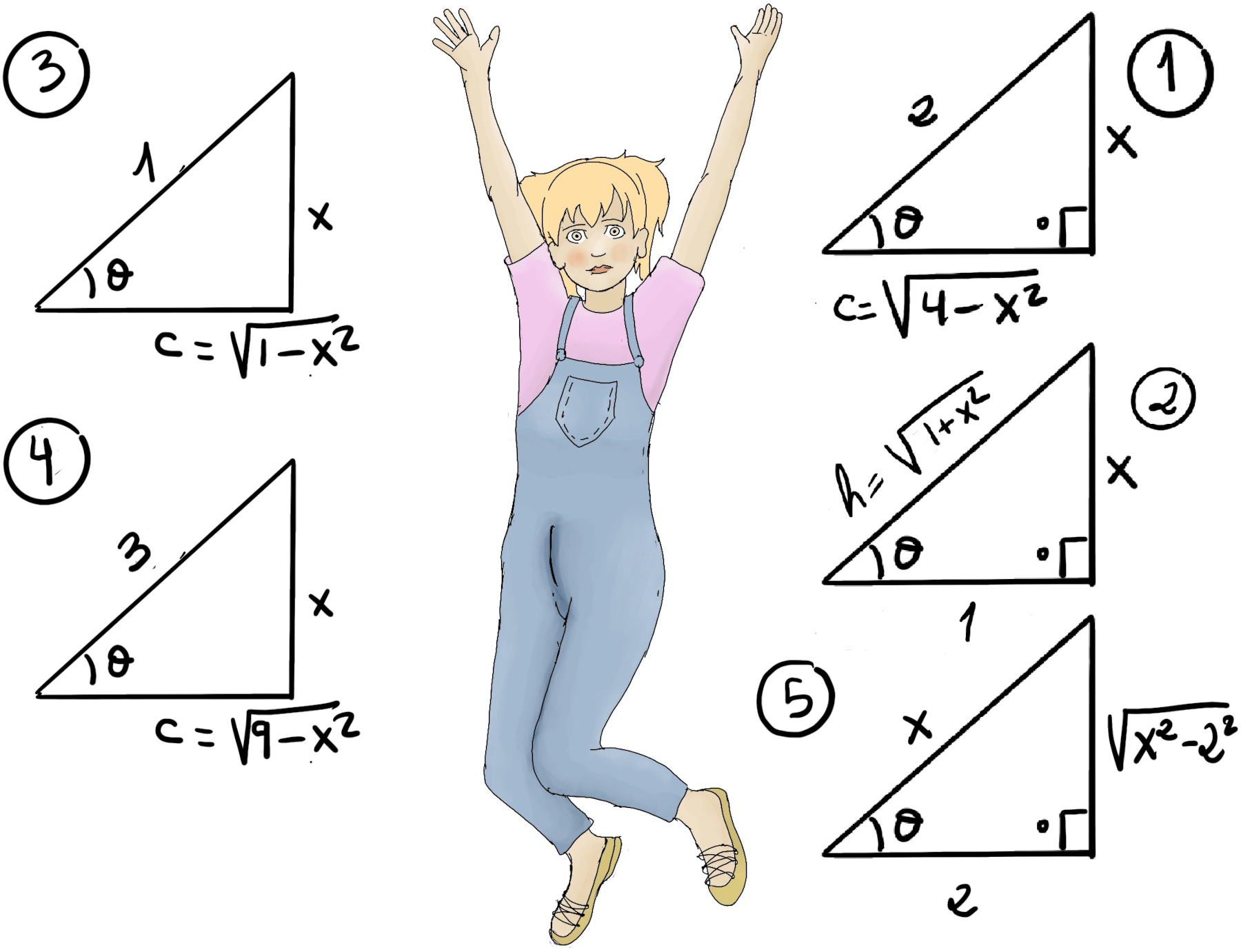
• $\int sec(x)dx$ [This is no an easy one to come up with 😃!. u = sec(x)+tan(x), Recall previous section, derivatives of Trigonometric Formulas, (sec(x)+tan(x))’=(sec(x)tan(x)+sec²(x))=(sec(x) +tan(x))·sec(x), u’ = u·sec(x) ⇒ sec(x) = ^u’⁄_u = ^d⁄_duln|u|] $\int sec(x)dx$ = ln|u| = ln|sec(x) + tan(x)| + C. [🚀]

• $\int \frac{\sqrt{x^2+1}}{x}dx =$[Trigonometry substitution, x = tan(θ), dx = sec²(θ)dθ] $\int \frac{\sqrt{tan^2(θ)+1}}{tan(θ)}sec^2(θ)dθ =$[Recall sec²(x) = 1 + tan²(x)] = $\int \frac{\sqrt{sec^2(θ)}}{tan(θ)}sec^2(θ)dθ = \int \frac{sec(θ)}{tan(θ)}sec^2(θ)dθ = \int csc(θ)(1+tan^2(θ))dθ = \int (csc(θ) + sec(θ)tan(θ))dθ = \int csc(θ)dθ + \int sec(θ)tan(θ)dθ$ =[Integration formulas for trigonometry, please notice that -ln|csc(θ)+cot(θ)| = ln|csc(θ)-cot(θ)|] $ ln|csc(θ)-cot(θ)| + sec(θ) + C.$

Now, we need to backtrack our substitution (Figure 2), $\frac{x}{1} = tan(θ).$ By the Pythagorean theorem, $1^2+x^2 = h^2 ⇒ h = \sqrt{1+x^2} ⇒ \int \frac{\sqrt{x^2+1}}{x}dx = ln|csc(θ)-cot(θ)| + sec(θ) + C = ln|\frac{\sqrt{1+x^2}}{x}-\frac{1}{x}|+\frac{\sqrt{1+x^2}}{1}+C = ln|\frac{\sqrt{1+x^2}-1}{x}|+\sqrt{1+x^2}+C.$

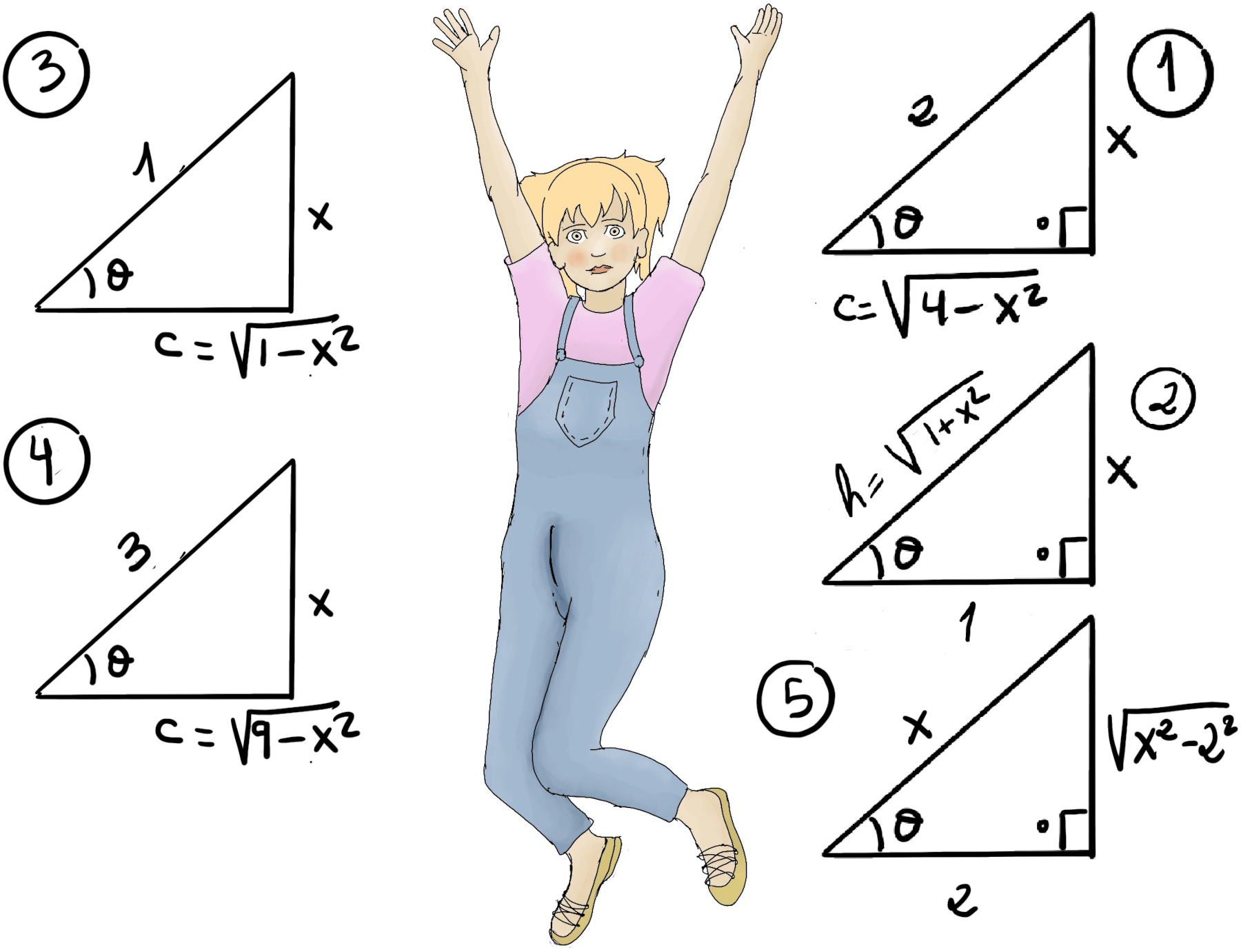
• Let’s try to solve $\int sin^n(x)cos^m(x)dx$, e.g., $\int sin^n(x)cos(x)dx$ =[Substitution u = sin(x), du = cos(x)dx] $\int u^ndu = \frac{u^{n+1}}{n+1} + C = \frac{sin^{n+1}(x)}{n+1} + C.$

• $\int sin^3(x)cos^2(x)dx$ =[sin²(θ) + cos²(θ) = 1] =$\int (1-cos^2(x))sin(x)cos^2(x)dx = \int (cos^2(x)-cos^4(x))sin(x)dx$ =[Substitution u = cos(x), du = -sin(x)dx] $\int (u^2-u^4)(-du) = -\frac{u^3}{3}+\frac{u^5}{5} + C= -\frac{cos^3(x)}{3}+\frac{cos^5(x)}{5} + C$.

• $\int sin^3(x)dx$ =[sin²(θ) + cos²(θ) = 1] =$\int (1-cos^2(x))sin(x)dx$ =[Substitution u = cos(x), du = -sin(x)dx] $\int (1-u^2)(-du) = \int (-1+u^2)du = -u + \frac{u^3}{3} + C = -cos(x)+\frac{cos^3(x)}{x} + C$.

• $\int cos^2(x)dx$ =[cos²(θ) = ^{(1 + cos(2θ))}⁄₂] $\int \frac{1+cos(2x)}{2}dx = \int \frac{1}{2}dx + \int \frac{cos(2x)}{2}dx$ =[U-substitution, 2x = u, 2dx = du] $\frac{x}{2} + \frac{sin(2x)}{4} + C$

• $\int sin^2(x)cos^2(x)dx$ =[$sin^2(x)cos^2(x) = \frac{1-cos(2x)}{2} \frac{1+cos(2x)}{2} = \frac{1-cos^2(2x)}{4} = \frac{1}{4}-\frac{1+cos(4x)}{8} = \frac{1}{8}-\frac{cos(4x)}{8}$] = $\int \frac{1}{8}-\frac{cos(4x)}{8}dx = \frac{x}{8}-\frac{sin(4x)}{8·4} + C = \frac{1}{8}(x -\frac{1}{4}sin(4x)) + C.$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
10. Professor Leonard.