Integration by parts

Failure is not an option. Failure is necessary…We try. We fail. We learn. We adjust, Craig Groeschel.

Recall

Antiderivatives are fundamental concepts in calculus. They are the inverse operation of derivatives.

Given a function f(x), an antiderivative, also known as indefinite integral, F, is the function that can be differentiated to obtain the original function, that is, F’ = f, e.g., 3x² -1 is the antiderivative of x³ -x +7 because $\frac{d}{dx} (x^3-x+7) = 3x^2 -1$. Symbolically, we write F(x) = $\int f(x)dx$.

The process of finding antiderivatives is called integration.

The Fundamental Theorem of Calculus states roughly that the integral of a function f over an interval is equal to the change of any antiderivate F (F'(x) = f(x)) between the ends of the interval, i.e., $\int_{a}^{b} f(x)dx = F(b)-F(a)=F(x) \bigg|_{a}^{b}$

There are several techniques used for integration, each suited to different types of integrals: U-Substitution or change of variables (The general form of an integrand which requires U-Substitution is ∫f(g(x))g’(x)dx. This can be rewritten as f(u)du. A big hint to use U-Substitution is that there is a composition of functions and there is some relation between two functions and their derivatives), Integration by Parts, Trigonometric Substitution and Integration by Trigonometric Identities, Partial Fractions decomposition, Improper integrals, and the use of some special functions.

Integration by parts

Integration by parts is a powerful technique used to integrate the product of two functions.

It is a technique used in calculus to evaluate integrals of the form $\int uv’dx$. The product rule states that the derivative of a product of two functions is the derivative of the first, times the second, plus the first times the derivative of the second, i.e., (uv)’ = u’v + uv’ ⇒ uv’ = (uv)’ -u’v ⇒ $\int uv’dx = uv -\int u’vdx$, e.g., $\int lnx dx =$[u = lnx, u’ = 1/xdx, v = x, v’ = dx] xlnx -$\int \frac{1}{x}xdx = xlnx -x + C.$ 🚀

One popular strategy to select which function to differentiate and which one to integrate is the LIATE mnemonic. It stands for “Logarithmic” (ln(x)), “Inverse trigonometric Functions” (arcsin(x), arccos(x), arctan(x)), “Algebraic” (xⁿ, x²+4, 3x +1), “Trigonometric” (sin(x), cos(x), tan(x)), and “Exponential” (e^x) functions. The term closer to E is the term usually integrated and the term closer to L is the term that is usually differentiated.

There is a second version, ILATE and this is the moral of the story: mnemonics are indeed useful guides, but they are aren’t set in stone, nothing replaces your intuition and experience.

Geometrical interpretation

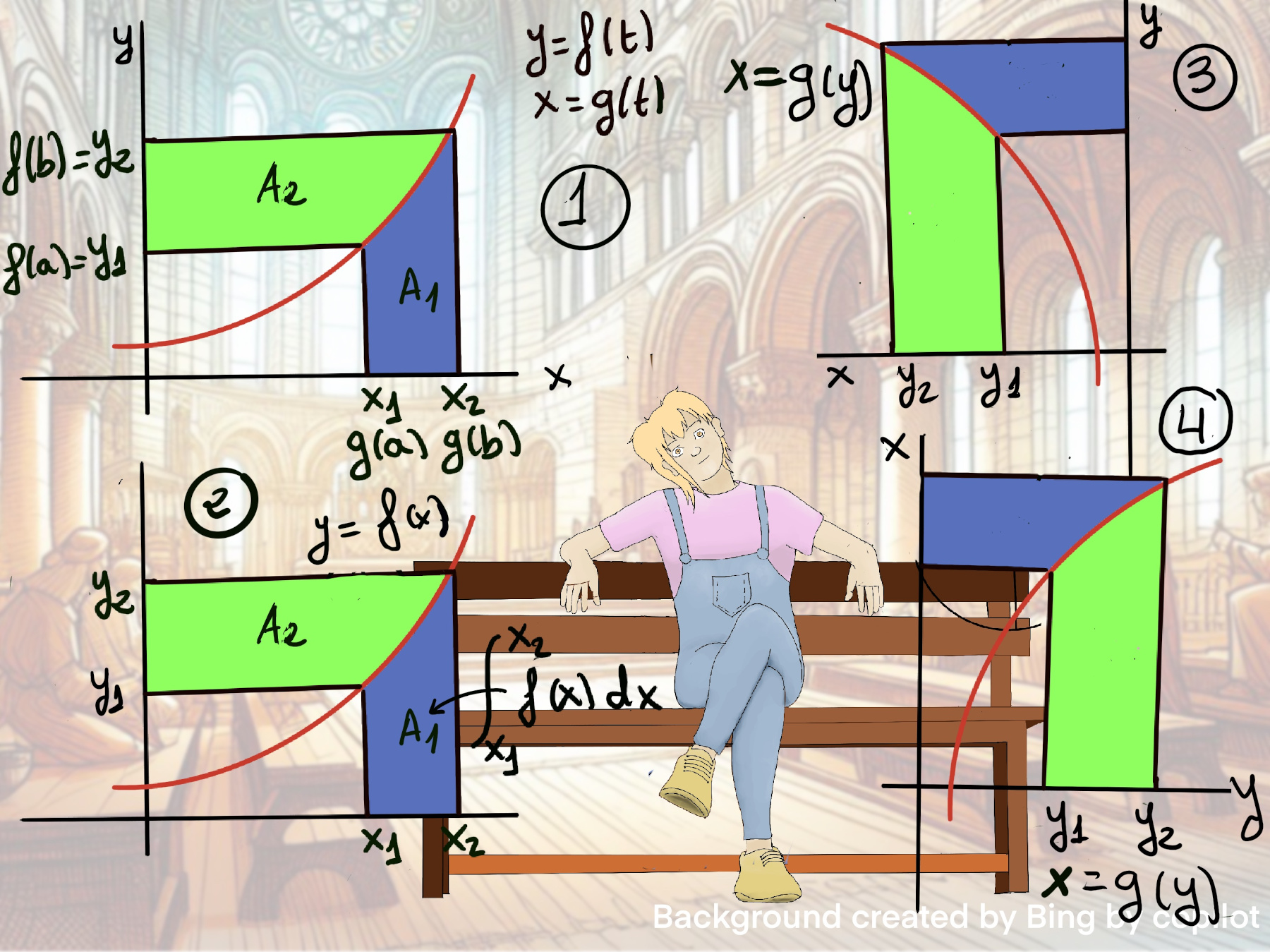
Let’s say we have a curve defined parametrically by y = f(t), x = g(t), and we want to find the areas between x₁ (=g(a), t = a) and x₂ -A₁- (=g(b), t = b) and between y₁ (=f(a), t = a) and y₂ (=f(b), t = b) -A₂- (Figure 1).

Notice that the sum of areas A₁ + A₂ = f(b)g(b) -f(a)g(a).

However, how we can compute these two areas individually? Well, let’s say that we have some function f(x) (Figure 2). $A_1=\int_{x_1}^{x_2} f(x)dx$.

And A₂? Let’s rotate our figure (Figure 3), and then flip it horizontally. Notice that the x and y axis have been swapped, hence this curve can be written x as a function of y, x = g(y) (Figure 4), and $A_2=\int_{y_1}^{y_2} g(y)dy = \int_{y_1}^{y_2} xdy$.

A₁ + A₂ = f(b)g(b) -f(a)g(a) ↭ $\int_{x_1}^{x_2} f(x)dx + \int_{y_1}^{y_2} xdy = f(b)g(b) -f(a)g(a) = f(t)g(t)\bigg|_{a}^{b}$ [🚀]

$\int_{x_1}^{x_2} f(x)dx + \int_{y_1}^{y_2} xdy = \int_{g(a)}^{g(b)} ydx + \int_{f(a)}^{f(b)} xdy$ =[Integration by substitution, y = f(t), x = g(t), dy = f’(t)dt, dx = g’(t)dt] $\int_{a}^{b} f(t)g’(t)dt + \int_{a}^{b} g(t)f’(t)dt =$[🚀] $f(t)g(t)\bigg|_{a}^{b}$

Rearrange this formula, $\int_{a}^{b} f(t)g’(t)dt= f(t)g(t)\bigg|_{a}^{b}$

$- \int_{a}^{b} g(t)f’(t)dt$

Solved exercises

• $\int 2x^2\sqrt{x+1}dx = \int 2x^2\sqrt{x+1}dx$ =[U-Substitution u = x+1, du = dx] $2\int (u-1)^2\sqrt{u}du = 2\int (u^2-2u+1)u^{\frac{1}{2}}du = 2\int (u^{\frac{5}{2}}-2u^{\frac{3}{2}}+u^{\frac{1}{2}})du = 2(\frac{2}{7}u^{\frac{7}{2}}-2\frac{2}{5}u^{\frac{5}{2}}+\frac{2}{3}u^{\frac{3}{2}}) = \frac{4}{7}(x+1)^{\frac{7}{2}}-\frac{8}{5}(x+1)^{\frac{5}{2}}+\frac{4}{3}(x+1)^{\frac{3}{2}}+C.$

• $\int xcos(x)dx$ =[Integral by parts, ∫udv = uv - ∫vdu. u = x, v’ = cos(x)dx, u’ = dx, v = sin(x)] $xsin(x)-\int sin(x)dx = xsin(x)+cos(x)+C.$

• $\int 3x^2(x^3+5)^7dx$= [Integrating using U-substitution, u = x³+5, du = 3x²dx] $\int u^7dx = \frac{u^8}{8} = \frac{(x^3+5)^8}{8}+ C.$

• $\int 6x^2ln(x)dx$ =[Integral by parts, ∫udv = uv - ∫vdu. u = ln(x), v’=6x²dx, u’ = ¹⁄_xdx, v = 2x³] $2x^3ln(x)-\int 2x^3\frac{1}{x}dx = 2x^3ln(x)-\int 2x^2dx = 2x^3ln(x)-\frac{2}{3}x^3+C.$

• $\int 2x(3x-2)^6dx$ =[Integral by parts, ∫udv = uv -∫vdu. u = 2x, v’ = (3x-2)⁶dx, u’ = 2dx, v = $\int (3x-2)^6dx = (Substitution,~ 3x-2 = u, 3dx = du) = \int \frac{1}{3}u^6du = \frac{1}{21}u^7= \frac{1}{21}(3x-2)^7$]= $2x\frac{1}{21}(3x-2)^7 -\int \frac{2}{21}(3x-2)^7dx$

$-\int \frac{2}{21}(3x-2)^7dx$ =[Substitution, 3x-2 = u, 3dx = du] $-\frac{2}{21}\int \frac{1}{3}u^7du = -\frac{2}{21}\frac{1}{3·8}(u)^8dx = -\frac{2}{21·3·8}(3x-2)^8 = -\frac{1}{252}(3x-2)^8$ ⇒ $\int 2x(3x-2)^6dx = 2x\frac{1}{21}(3x-2)^7 -\frac{1}{252}(2x-2)^8 = \frac{2x}{21}(3x-2)^7 -\frac{1}{252}(3x-2)^8+ C = \frac{24x}{252}(3x-2)^7 -\frac{3x-2}{252}(3x-2)^7+ C = \frac{21x+2}{252}(3x-2)^7 + C.$

• $\int x^2sin(x)dx$ =[u = x², v’ = sin(x)dx, u’ = 2xdx, v = -cos(x)] $x^2(-cos(x))-\int (-cos(x))2xdx = -x^2·cos(x)+2\int cos(x)xdx$ =[u = x, v’ = cos(x)dx, u’ = dx, v = sin(x)] = $-x^2·cos(x)+2(x·sin(x) -\int sin(x)dx) = -x^2·cos(x)+2(x·sin(x)-(-cos(x))) = -x^2cos(x)+2xsin(x)+2cos(x)+C.$

• $\int (lnx)^2 dx =$[u = (lnx)², u’=2(lnx)(1/x), v = x, v’ = dx] x(lnx)² -$\int 2(lnx)\frac{1}{x}xdx = x(lnx)^2 -\int 2(lnx)dx$ =[By the previous exercise, 🚀] x(lnx)² -2(xlnx -x) + C. 🚂

• In the general case, $\int (lnx)^n dx =$[u = (lnx)ⁿ, u’ = n(lnx)^n-1(1/x)dx, v = x, v’ = dx] x(lnx)ⁿ -n$\int (lnx)^{n-1}\frac{1}{x}x dx = x(lnx)^n -n\int (lnx)^{n-1}dx$.

If we define F_n(x) = $\int (lnx)^n dx$, F_n(x) = x(lnx)ⁿ -nF_n-1(x). Hence, F₀(x) = $\int (lnx)^0 dx = x$, F₁(x) = x(lnx) -F₀(x) = xlnx -x + C🚀, F₂(x) = x(lnx)² -2F₁(x) = x(lnx)² -2(xlnx -x) + C 🚂 and so on…

• $\int x^ne^xdx$ =[u = xⁿ, u’ = nx^n-1dx, v’ = e^xdx ⇒ v = e^x] xⁿe^x -$\int nx^{n-1}e^xdx$, so F_n(x) = $\int x^ne^xdx = x^ne^x -nF_{n-1}(x)$.

F₀(x) = $\int e^xdx = e^x + C.$ F₁(x) = $\int xe^xdx$ = xe^x -e^x + C, and so on…

• $\int x^5\sqrt{x^3+1}dx =$[u=x³, v’=$x^2\sqrt{x^3+1}dx$, u’=3x²dx, v =$\int x^2\sqrt{x^3+1}dx = $(x³+1 = r, 3x²dx = dr) =$\frac{1}{3}\int \sqrt{r}dr = \frac{1}{3}\frac{2}{3}r^{\frac{3}{2}} = \frac{2}{9}r^{\frac{3}{2}} = \frac{2}{9}(x^3+1)^{\frac{3}{2}}$] = $x^3\frac{2}{9}(x^3+1)^{\frac{3}{2}}-\frac{2}{9}\int 3x^2(x^3+1)^{\frac{3}{2}}dx = x^3\frac{2}{9}(x^3+1)^{\frac{3}{2}}-\frac{2}{3}\int x^2(x^3+1)^{\frac{3}{2}}dx =$[x³+1 = r, 3x²dx = dr] $\frac{2}{9}x^3(x^3+1)^{\frac{3}{2}}-\frac{2}{3}\frac{1}{3}\frac{2}{5}(x^3+1)^{\frac{5}{2}} = \frac{2}{9}x^3(x^3+1)^{\frac{3}{2}}-\frac{4}{45}(x^3+1)^{\frac{5}{2}}+C.$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.