Derivate 2: Exponential and Logarithms

A learning experience is one of those things that says, ‘You know that thing you just did? Don’t do that, Douglas Adams

Recall

The derivative of a function at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. It is the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable.

Definition. A function f(x) is differentiable at a point “a” of its domain, if its domain contains an open interval containing “a”, and the limit $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$ exists, f’(a) = L = $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$. More formally, for every positive real number ε, there exists a positive real number δ, such that for every h satisfying 0 < |h| < δ, then |L-$\frac {f(a+h)-f(a)}{h}$|< ε.

Basic important derivatives

1. Power Rule: $\frac{d}{dx}(x^n) = nx^{n-1}$.
2. Sum Rule: $\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))$
3. Product Rule: $\frac{d}{dx}(f(x) \cdot g(x)) = f’(x)g(x) + f(x)g’(x)$.
4. Quotient Rule: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f’(x)g(x) - f(x)g’(x)}{(g(x))^2}$
5. Chain Rule: $\frac{d}{dx}(f(g(x))) = f’(g(x)) \cdot g’(x)$
6. $\frac{d}{dx}(e^x) = e^x, \frac{d}{dx}(\ln(x)) = \frac{1}{x}, \frac{d}{dx}(\sin(x)) = \cos(x), \frac{d}{dx}(\cos(x)) = -\sin(x), \frac{d}{dx}(\tan(x)) = \sec^2(x), \frac{d}{dx}(\arcsin(x)) = \frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arccos(x)) = -\frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arctan(x)) = \frac{1}{1 + x^2}.$

Derivate of Exponential and Logarithms functions.

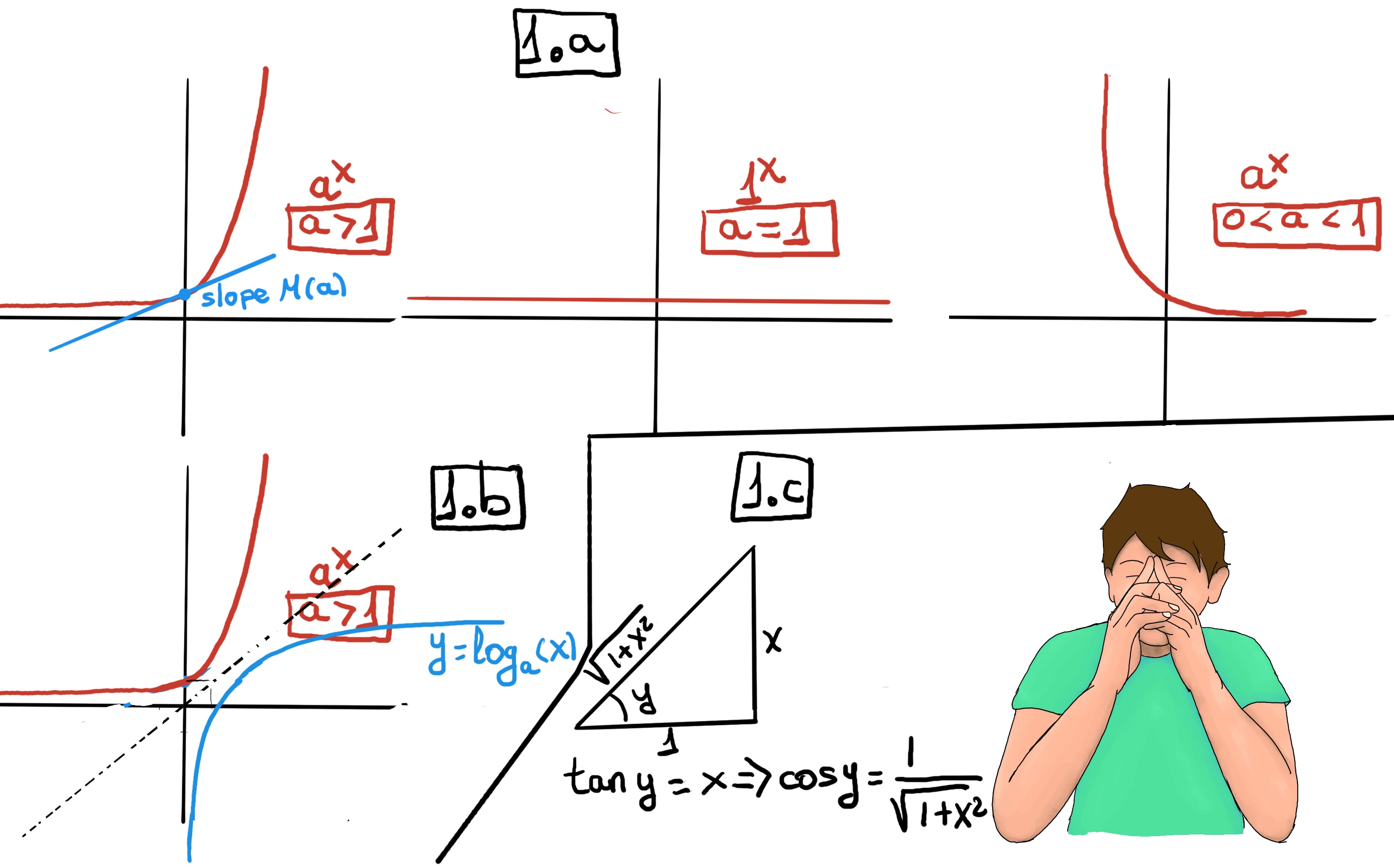
An exponential function is a function of the form f(x) = a^x, where “x” is a variable and “a” is a constant which is called the base of the function and it should be a positive real number (a>0).  

Recall that a^m/n= $\sqrt[n]{a^{m}}$

f(x)=a^x, let’s calculate $\frac{d}{dx}a^{x}$

f’(x) = $\frac{d}{dx}a^{x} =~ \lim_{h \to 0} \frac{a^{x+h}-a^{x}}{h} =$[Recall, a^xa^y=a^x+y] $\lim_{h \to 0}a^{x}\frac{a^h-1}{h} = a^{x}·\lim_{h \to 0}\frac{a^h-1}{h}$

Let’s define M(a) = $\lim_{h \to 0}\frac{a^h-1}{h}$. It is the slope of a^x at x = 0 because $\frac{d}{dx}a^{x} \vert_{x=0} =~ a^{0}M(a)=~ M(a)$

In conclusion, f'(x) = $\frac{d}{dx}a^{x} = M(a)a^{x}$.

Definition. The number e =2.71828182845905…, also known as Euler’s number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways.

1. e = $\lim_{n \to ∞}(1+\frac{1}{n})^n$
2. e = $\sum_{n=0}^\infty \frac{1}{n!}$
3. It is the unique positive number 'a' such that the graph of the function y=a^x has a slope of 1 at x = 0 ↭ M(e)=1 ↭ e is the unique positive number for which $\lim_{h \to 0}\frac{e^h-1}{h} = 1$ -1.a.-

Therefore, let a = e, $\frac{d}{dx}a^{x} = M(a)a^{x} ⇨$[M(e)=1] $\frac{d}{dx}e^{x} = e^{x}$. The exponential function, denoted as f(x)=e^x, has a unique property that its derivative is the same as the function itself.

As it was expected, f(x) = e^x, $f’(0)$ = $e^{x}|_{x=0}=1$

Let a=2, f(x)=2^x. Then, f(kx)=2^kx=(2^k)^x=b^x where b=2^k.

$\frac{d}{dx}b^{x} = \frac{d}{dx}f(kx)=$[Constant Multiple Rule (c·g(x))’ = c·g’(x)] $kf’(kx)$.

We evaluate at x = 0, $\frac{d}{dx}b^{x}|_{x=0}=kf’(0)$ [Recall f(x)=2^x, f’(x)=M(2)2^x] =$k·M(2)·2^0 = k·M(2)$. Therefore, b=e ↭ kM(2) = 1 ↭ k=$\frac{1}{M(2)}$

• We call the inverse of a^x the logarithmic function with base a, that is, log_ax=y ↔ a^y=x. The logarithm with base e is the natural logarithm. The natural logarithm is the inverse of e^x, that is, lnx=y ↔ a^y=x, -1.b.-

• Let w = lnx, we want to calculate $\frac{d}{dx}lnx$.

By definition (w = lnx), e^w = x, $\frac{d}{dx}e^{w}= \frac{d}{dx} x = 1$🚀

$\frac{d}{dx}e^{w}=\frac{d}{dw}e^{w}\frac{dw}{dx} = e^{w}\frac{dw}{dx} = $[🚀]1. Therefore, $\frac{dw}{dx}=\frac{1}{e^w}$ where w = lnx and obviously e^w=x ⇒$\frac{d}{dx}lnx=\frac{1}{x}$

• Let’s calculate $\frac{d}{dx}a^{x}$. $\frac{d}{dx}a^{x}=~ \frac{d}{dx}((e^{lna})^x)=~ \frac{d}{dx}e^{xlna}$=[The Chain rule] $e^{xlna}·lna=a^{x}·lna$

$\frac{d}{dx}a^{x}=(lna)a^{x}$, so M(a)=lna.

$(lnu)’=\frac{d}{dx}lnu = \frac{d}{du}lnu\frac{du}{dx} = \frac{1}{u}u’=\frac{u’}{u}$

Another way of getting the same result regarding $\frac{d}{dx}a^{x}$ is by using the substitution u = a^x, so lnu = ln(a^x) = x·lna, and therefore, (lnu)’=lna,

$(lnu)’=\frac{u’}{u}=lna~⇨~ u’=u·lna⇨~ \frac{d}{dx}a^{x} = (lna)·a^{x}$

• Let’s calculate $\frac{d}{dx} log_a(x)$. By definition, w = log_a(x), a^w = x, $\frac{d}{dx} a^w = \frac{d}{dx} x = 1.$ 🚀

$\frac{d}{dx} a^w = \frac{d}{dw}a^w\frac{dw}{dx} = a^w·ln(a)\frac{dw}{dx}$ =[🚀]1 ⇒ $\frac{dw}{dx} = \frac{1}{a^w·ln(a)}$ ⇒[a^w = x, w = log_a(x)] $\frac{d}{dx}log_a(x) = \frac{1}{x·ln(a)}$

• Let’s calculate $\lim_{n \to \infin}(1+\frac{1}{n})^{n}$

$ln((1+\frac{1}{n})^{n})$ = $n·ln(1+\frac{1}{n})$ =[Consider $\Delta x=\frac{1}{n}$] $\frac{1}{\Delta x}ln(1+\Delta x) =$[ln1 = 0] $\frac{1}{\Delta x}(ln(1+\Delta x)-ln1)$

And therefore, $lim_{n \to \infin} ln((1+\frac{1}{n})^{n}) = \lim_{\Delta x \to 0} \frac{1}{\Delta x}(ln(1+\Delta x)-ln1) = \lim_{\Delta x \to 0} \frac{ln(1+\Delta x)-ln1}{\Delta x}$, and this is $\frac{d}{dx} lnx|_ {x=1} =~ \frac{1}{x}|_{x=1} = 1$ 🚀

$\lim_{n \to \infin}(1+\frac{1}{n})^{n} = lim_{n \to \infin}e^{ln((1+\frac{1}{n})^{n})} =$[Power law for limits] $e^{lim_{n \to \infin} ln((1+\frac{1}{n})^{n})}=$[🚀] e¹ = e.

The number e =2.71828182845905…, also known as Euler’s number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. e could be defined as the limit of (1 + ¹⁄_n)ⁿ as n approaches infinity, e = $\lim_{n \to \infin}(1+\frac{1}{n})^{n}.$

• Let’s demonstrate the power rule for real exponents. If u(x)=x^r, then u’(x)=rx^r-1, ∀r ∈ ℝ.

$x^{r}=e^{ln(x^{r})}=e^{r·lnx}$ ⇨ $\frac{d}{dx}x^{r}$=[The chain rule]$\frac{r}{x}e^{rlnx}=\frac{r}{x}x^{r}=rx^{r-1}$

Another way of getting the same result is as follows, let $u=x^{r}, ~lnu=rlnx$ ⇨ $\frac{u’}{u}=\frac{r}{x}⇨~ u’=\frac{u}{x}r=\frac{x^r}{x}r = rx^{r-1}$

Summary

Exponential functions:

1. $\frac{d}{dx} e^x = e^x$
2. $\frac{d}{dx} a^x = a^x \cdot \ln(a)$, where a is a constant.

Logarithmic functions:

1. $\frac{d}{dx} \ln(x) = \frac{1}{x}$
2. $\frac{d}{dx} \log_a(x) = \frac{1}{x \cdot \ln(a)}$, where a is the base of the logarithm.

Solved exercises

• $\frac{d}{dx}ln(x)·sin(x) = ln(x)·cos(x)+\frac{sin(x)}{x}$

• $\frac{d}{dx} log_5x^2 = \frac{2x}{ln(5)·x^2} = \frac{2}{ln(5)·x}$

• $\frac{d}{dx}e^{xtan^{-1}x} = e^{xtan^{-1}x}(tan^{-1}x + \frac{x}{1+x^{2}})$

• $\frac{d}{dx} 3e^x+10x^3ln(x) = 3·e^x+30·x^2·ln(x)+10x^3\frac{1}{x} = 3·e^x+30·x^2·ln(x)+10x^2.$

• $\frac{d}{dx} (2x^4+1)^{tan(x)}$⇒[y = $(2x^4+1)^{tan(x)}$]ln(y) = $ln((2x^4+1)^{tan(x)}) = tan(x)ln(2x^4+1)$ ⇒[Differentiate both sides, tan’(x) = sec²(x)] $\frac{1}{y}\frac{dy}{dx} = sec^2(x)·ln(2x^4+1)+ \frac{8x^3}{2x^4+1}·tan(x)$ ⇒ $\frac{dy}{dx} = y·(sec^2(x)·ln(2x^4+1)+ \frac{8x^3}{2x^4+1}·tan(x)) = (2x^4+1)^{tan(x)}·(sec^2(x)·ln(2x^4+1)+ \frac{8x^3}{2x^4+1}·tan(x)).$

• $\frac{d}{dx}\frac{e^x+e^{-x}}{e^x-e^{-x}} =\frac{(e^x-e^{-x})·(e^x-e^{-x})-(e^x+e^{-x})(e^x+e^{-x})}{(e^x-e^{-x})^2} = \frac{(e^x-e^{-x})^2-(e^x+e^{-x})^2}{(e^x-e^{-x})^2} =$[a²-b² = (a-b)(a+b) where a = e^x-e^-x and b = e^x+e^-x] $\frac{(e^x-e^{-x}-e^x-e^{-x})(e^x-e^{-x}+e^x+e^{-x})}{(e^x-e^{-x})^2} = \frac{-2e^{-x}·2e^x}{(e^x-e^{-x})^2} = \frac{-4}{(e^x-e^{-x})^2}$

• $\frac{d}{dx} x^x$, let u=x^x, lnu=x·lnx ⇨ $(lnu)’=lnx + x\frac{1}{x} = lnx + 1 ⇨~ \frac{u’}{u}= lnx + 1⇨~ u’= u(lnx+1) = x^{x}(lnx+1).$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus.
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
9. blackpenredpen.