If you torture data long enough, it will confess to anything or, in other words, there are different types of lies: white lies, seemingly small exaggerations and half-truths, damn lies, out-of-context information, and misleading statistics, #Anawim, justtothepoint.com.
Recall
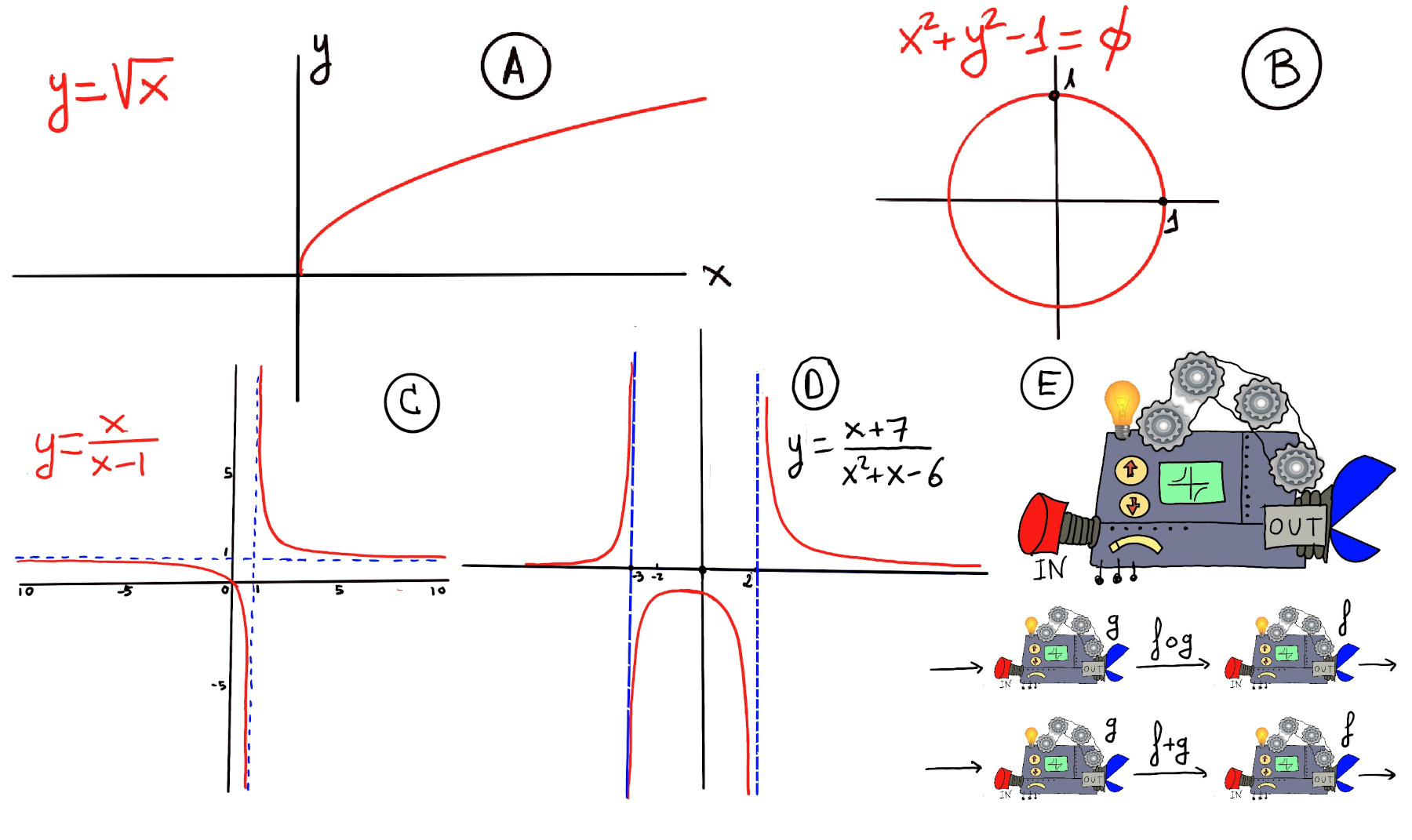
Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).
The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ. A mathematical function is like a black box that takes certain input values and generates corresponding output values (Figure E).
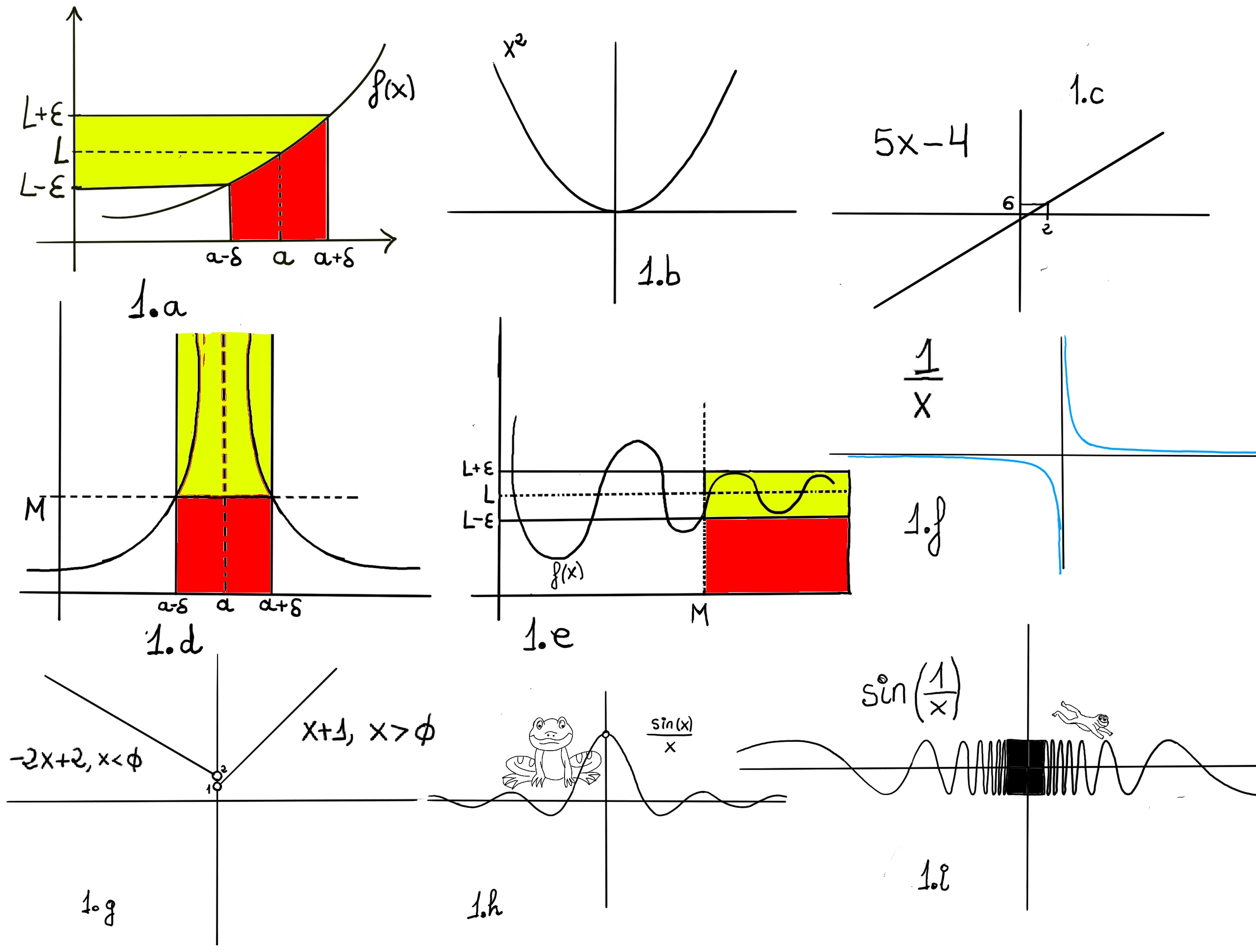
Very loosing speaking, a limit is the value to which a function grows close as the input get closer and closer to some other given value.
One would say that the limit of f, as x approaches a, is L, $\lim_{x \to a} f(x)=L$. Formally, for every real ε > 0, there exists a real δ > 0 such that for all real x, 0 < | x − a | < δ implies that | f(x) − L | < ε. In other words, f(x) gets closer and closer to L, f(x)∈ (L-ε, L+ε), as x moves closer and closer -approaching closer but never touching- to a (x ∈ (a-δ, a+δ), x≠a)) -Fig 1.a.-
 Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = L$ if
Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = L$ if
$\forall \epsilon>0, \exists \delta>0: 0<|x-a|<\delta, implies~ |f(x)-L|<\epsilon$
Or
$\forall \epsilon>0, \exists \delta>0: |f(x)-L|<\epsilon, whenever~ 0<|x-a|<\delta$
The Limit laws
Let f(x), g(x) be functions defined on an interval that contains x = a, except possibly at x = a, assume that L and M are real numbers such that $ \lim_{x \to a} f(x) = L$ and $\lim_{x \to a} g(x) = M$. Let c be a constant. Then, each of the following statements holds:
- Limit of a constant. The limit of a constant function is equal to the constant, $\lim_{x \to a} k = k$ where k is a constant, e.g., $lim_{x \to 12} 7 = 7$.
- Sum law for limits. It states that the limit of the sum of two functions equals the sum of the limits of both functions, that is, $\lim_{x \to a} (f(x)+g(x)) = lim_{x \to a} f(x) + lim_{x \to a} g(x) = L + M,$ e.g., $lim_{x \to 2}(2x+7) = lim_{x \to 2}(2x) + lim_{x \to 2}(7) = 4+7 = 11.$
Proof: Let $\epsilon>0$
$\exists \delta_1>0: 0<|x-a|<\delta_1, implies~ |f(x)-L|<\frac{\epsilon}{2}$
$\exists \delta_2>0: 0<|x-a|<\delta_2, implies~ |g(x)-M|<\frac{\epsilon}{2}$
Let’s choose $\delta = min (\delta_1, \delta_2).$
$\forall \epsilon>0, \exists \delta>0: 0<|x-a|<\delta$ ⇒[By the triangle inequality, |a+b|≤|a|+|b|] |f(x)+g(x)-L-M| ≤ |f(x)-L|+ |g(x)-M| $<\frac{\epsilon}{2} + <\frac{\epsilon}{2} = \epsilon$
- Difference law for limits. It states that the limit of the difference of two functions equals the difference of the limits of both functions, that is, $\lim_{x \to a} (f(x)-g(x)) = lim_{x \to a} f(x) - lim_{x \to a} g(x) = L - M,$ e.g., $lim_{x \to 2}(2x-7) = lim_{x \to 2}(2x) - lim_{x \to 2}(7) = 4-7 = -3.$
- Constant multiple law for limits. $\lim_{x \to a} c·f(x) = c·lim_{x \to a} f(x) = c·L,$ e.g., $\lim_{x \to 1} 7x^3 = 7·\lim_{x \to 1} x^3 = 7·1 = 7.$
- Product law for limits. It states that the limit of a product of two functions equals the product of the limits of both functions, that is, $\lim_{x \to a} (f(x)·g(x)) = lim_{x \to a} f(x) · lim_{x \to a} g(x) = L · M.$
$\lim_{x \to 2} x^2·(x+1) = \lim_{x \to 2} x^2·\lim_{x \to 2} x+1 = 4·3 = 12.$
$\lim_{x \to 2} (6x-x^3)·(x^2+3x-1) = \lim_{x \to 2} 6x-x^3·\lim_{x \to 2} x^2+3x-1 = 4·9 = 36.$
$\lim_{x \to 5} (2x^2-3x+4) = \lim_{x \to 5}(2x^2) - \lim_{x \to 5}(3x) + \lim_{x \to 5}(4) = 2·\lim_{x \to 5}(x^2) - 3·\lim_{x \to 5}(x) + \lim_{x \to 5}(4) = 2·5^2-3·5+4 = 39.$
Proof.
Let $\epsilon>0$
$\exists \delta>0: 0<|x-a|<\delta, implies~ |f(x)g(x)-LM|<\epsilon$
|f(x)g(x)-LM| = |f(x)g(x) -Lg(x) + Lg(x) -LM| = |g(x)(f(x)-L) + L(g(x)-M)| ≤[Triangle inequality] |g(x)(f(x)-L)| + |L(g(x)-M)| = |g(x)(f(x)-L)| + |L(g(x)-M)| = |g(x)||(f(x)-L)| + |L||(g(x)-M)|
This is the 🔑 tricky part:
- $lim_{x \to a} g(x)$ = M ⇒ Let $\frac{ε}{2(|L|+1)}, \exists \delta_1>0: 0<|x-a|<\delta_1, implies~ |g(x)-M|<\frac{ε}{2(|L|+1)}.$
- Let $ε = 1> 0, \exists \delta_2>0: 0<|x-a|<\delta_2, implies~ |g(x)-M|<1⇒|g(x)| = |g(x) -M +M| ≤ |g(x) -M| + |M|< 1 + |M|.$
- $lim_{x \to a} f(x)$ = L ⇒ Let $\frac{ε}{2(|M|+1)}, \exists \delta_3>0: 0<|x-a|<\delta_3, implies~ |f(x)-L|<\frac{ε}{2(|M|+1)}.$
We choose δ = min{δ1, δ2, δ3}
|f(x)g(x)-LM| ≤ |g(x)||(f(x)-L)| + |L||(g(x)-M)| < $(1+|M|)\frac{ε}{2(|M|+1)}+|L|\frac{ε}{2(|L|+1)}<\frac{ε}{2}+|L|\frac{ε}{2|L|} = \frac{ε}{2}+\frac{ε}{2} = ε$∎
- Quotient law for limits. $\lim_{x \to a} \frac{f(x)}{g(x)} = \frac{\lim_{x \to a} f(x)}{\lim_{x \to a} g(x)} = \frac{L}{M}$, e.g., $\lim_{x \to 2} \frac{x^2-1}{x-1} = \frac{\lim_{x \to 2} x^2-1}{\lim_{x \to 2} x-1} = \frac{3}{1} = 3.$
- Power law for limits. It states that the limit of the nth power of a function equals the nth power of the limit of the function, that is, $\lim_{x \to a} (f(x))^{n} = (\lim_{x \to a} f(x))^{n} = L^{n},$ e.g., $\lim_{x \to 5} (x+1)^{2} = (\lim_{x \to 5} x+1)^{2} = 6^{2} = 36.$
- Root law for limits. $\lim_{x \to a} \sqrt[n]{f(x)} = \sqrt[n]{\lim_{x \to a} f(x)} = \sqrt[n]{L} $ for all L if n is odd and for L≥0 if n is even.
$\lim_{x \to 2} \sqrt{x^2+3x-1} = \sqrt{\lim_{x \to 2} x^2+3x-1} = \sqrt{9} = 3$
$\lim_{x \to 2} \sqrt[3]{\frac{5x+22}{2x}} = \sqrt[3]{\lim_{x \to 2} {\frac{5x+22}{2x}}} = \sqrt[3]{\frac{5·2+22}{2·2}} = \sqrt[3]{8} = 2.$
- Limit of a polynomial. $\lim_{x \to a} a_nx^n + a_{n-1}x^{n-1} + \ldots + a_2x^2 + a_1x + a_0 = a_n·a^n + a_{n-1}·a^{n-1} + \ldots + a_2·a^2 + a_1·a + a_0$, e.g., $\lim_{x \to 2} 3x^2-5x+7 = 3·2^2-5·2+7 = 12-10+7 = 9$.
- Limit of a composite function. The limit of a composition is the composition of the limit, provided
the outside function is continuous at the limit of the inside function. $\lim_{x \to a} f ◦ g(x) = \lim_{x \to a} f(g(x)) = f(\lim_{x \to a} g(x))$ if f is continuous at
$\lim_{x \to a} g(x).$
$\lim_{x \to 1} sin(\frac{π}{x+1}) = sin(\lim_{x \to 1} \frac{π}{x+1}) = sin(\frac{π}{2}) = 1.$
$\lim_{x \to 0} ln(cos(x)) = ln(\lim_{x \to 0} cos(x)) = ln(1)=$ [Recall e0 = 1] 0.
$\lim_{x \to ∞} cos(\frac{1}{x}) = cos(\lim_{x \to ∞} \frac{1}{x}) = cos(0) = 1.$
$\lim_{x \to 0⁺} x^x = $[$e^{ln(x^x)}=e^{x·ln(x)}$] $\lim_{x \to 0⁺} e^{x·ln(x)} = e^{\lim_{x \to 0⁺} x·ln(x)} = e^{\lim_{x \to 0⁺} \frac{ln(x)}{\frac{1}{x}}}=$[ L’Hospital’s Rule] $e^{\lim_{x \to 0⁺} \frac{\frac{1}{x}}{\frac{-1}{x^2}}} = e^{\lim_{x \to 0⁺} -x} = e^0 = 1.$
Bibliography
This content is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
- NPTEL-NOC IITM, Introduction to Galois Theory.
- Algebra, Second Edition, by Michael Artin.
- LibreTexts, Calculus.
- Field and Galois Theory, by Patrick Morandi. Springer.
- Michael Penn, and MathMajor.
- Contemporary Abstract Algebra, Joseph, A. Gallian.
- YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
- Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
- blackpenredpen.







 Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = L$ if
Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = L$ if