Functions or Mappings

Brick walls are there for a reason. The brick walls are not there to keep us out. The brick walls are there to show how badly we want something. Because the brick walls are there to stop the people who don’t want something badly enough. They are there to keep out the other people, Randy Pausch.

Definitions.

Let A and B be two arbitrary sets.

1. The Cartesian product of two sets A and B, denoted A x B, is the set of all possible ordered pairs (a, b), where the first element of each pair, a, is an element of A, and the second, b, is an element of B. We could express this in a more mathematical or formal language as A x B = {(a, b): a ∈ A and b ∈ B}, e.g., {1, 2} x {red, yellow, blue} = {(1, red), (1, yellow), (1, blue), (2, red), (2, yellow), (2, blue)}
2. A relation R is a subset of the Cartesian product, R ⊆ A x B.
3. A function is a triplet (Φ, A, B), where A and B are sets, and Φ ⊆ A x B is a relation, function or mapping from A to B. A function Φ : A → B assigns to each element of a (for each a ∈ A or ∀ a ∈ A) exactly one element of B (f(a) ∈ B).The sets A, B are called the domain and codomain of the function respectively. Functions are also called maps or mappings (1.a).

A function is just a collection of ordered pairs of the form (a, b) where a ∈ A and b ∈ B that satisfies one condition: every element a in the domain A must be paired with exactly one element b in the codomain B. The first elements are called arguments, the second values.

A way of representing the set of ordered pairs which define a function is to use one of these notations: {(x,y)| y = f(x), x ∈ X} or {(x, f(x))| x ∈ X}.

Counterexamples

• 1.c’s diagram represents the set of pairs {(1, A), (2, B), (3, C), (3, D)}. It does not define a function because: (i) 3 is in more than one ordered pair, namely (3, C) and (3, D); (ii) 4 is not a first element (input) of any ordered pair.

• f = {(x, y) ∈ ℤ x ℤ | 2x -3y = 1} is not a function either because (1, y)∉f ∀y∈ℤ (1 is not a first element of any ordered pair). Suppose for the sake of contradiction, ∃y: 2·1 -3·y = 1 ⇒ -3·y = -1 ⇒ y = 1/3 ∉ ℤ ⊥

A function is most often denoted by letters such as f, g, or h. A function takes an input element from the set A (X) and produces an output in the set B (Y). We can image it as some sort of black box, device, or machine that does some kind of computation or transformation (1.b). You put some object into its input funnel, then the function machine will process that object or argument and turn it into some other object or value, which comes out as output.  

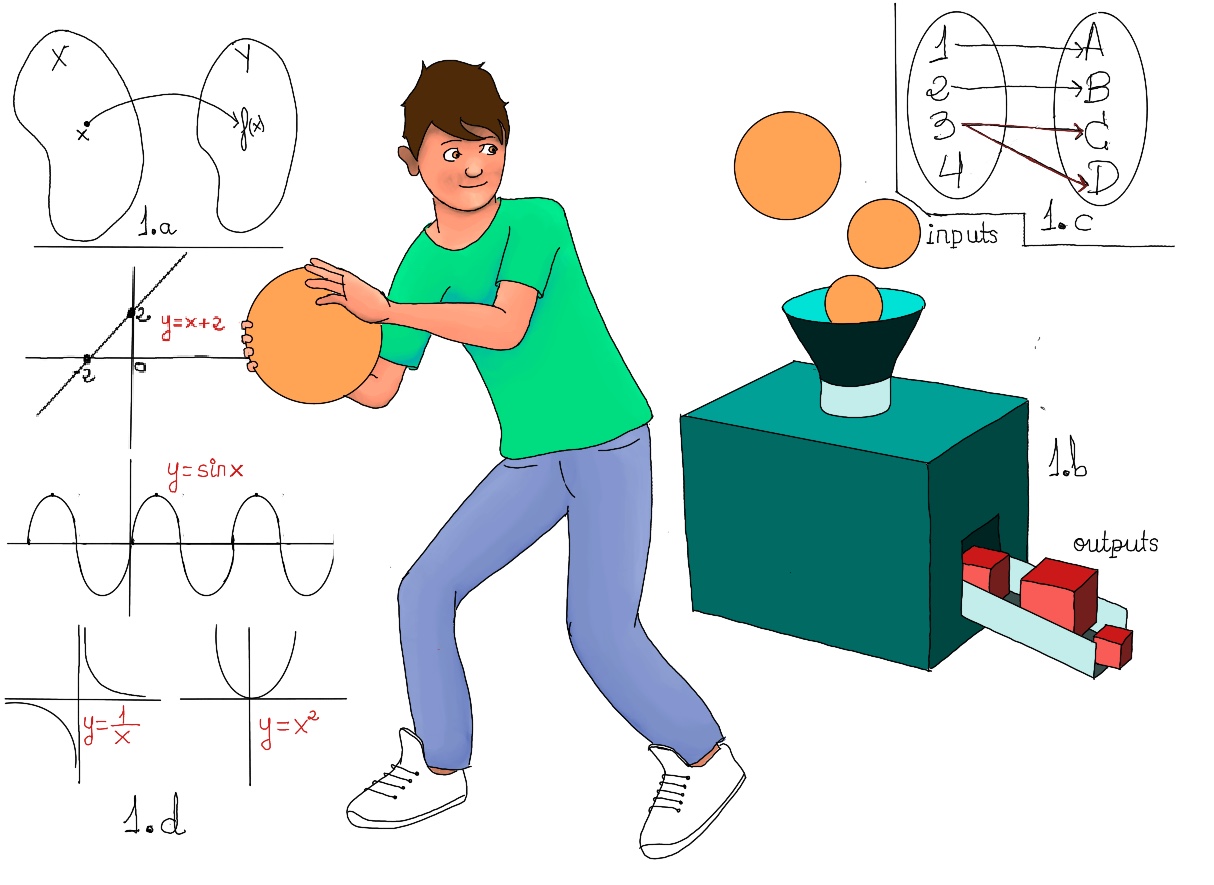
Let’s see some examples:

1. f: ℝ → ℝ, f(x)=x^2 is a well-defined function.
2. f: ℝ → ℝ, f(x)=x + 2 is a well-defined function. Besides, 2x + 3, 3x -1, x² + 2x +1, x³, x²+4x +3, etc. are all well-defined functions
3. A function is ill-defined if it is ambiguous what the output should be or there is no output for some given input, e.g., f: ℝ → ℝ, f(x)=¹⁄_x has no output for x = 0; f(x) = $\sqrt{x}$ is undefined for negative numbers; the tangent function is undefined for $\frac{π}{2}+2kπ, k∈\mathbb{Z}$; f(x) = y² is not well-defined because f(4) could be 2 (2² = 4) or -2 (2^-2 = 4). The logarithmic function log_b(x) (for any positive real number b≠1) is defined only for x > 0.
4. The identity function is a function that always returns the same value that was used as its argument, unchanged. id_X: X → X is defined by id_X(x) = x, ∀ x ∈ X.
5. Consider the function f: ℚ → ℤ given by f(p/q) = p. We know that 1/2 = 2/4 = 3/6 =··· then, what is it f(1/2)? This relation is not well-defined.
6. Let f = {(x, y) ∈ ℤ x ℤ | 4x -2y = 2}. f is a function, and can be rewritten as follows, 4x -2y = 2 ↭ y = 2x -1 ↭ {(x, 2x-1)| x ∈ ℤ}.
7. Let A = {a, b, c}, and let P(A) be the power set of A (the set of all subsets of the set A), P(A) = {∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}, and let f be the function “cardinality” that counts the number of element of any given set X (that is a subset of A): P(A) → ℕ, f(X) = |X|. ∅ → 0; {a}, {b}, {c} → 1; {a, b}, {a, c}, {b, c} → 2; {a, b, c} → 3.

The set A (or X) is called the domain of f, the set B (or Y) is called the codomain of f. The image or range of a function f: X → Y is simply the set of all possible outputs or values it may produce under the mapping or transformation given by f, that is, f(X) = {y | y = f(x), x ∈ X } ⊆ Y. The graph of the function is the set of all ordered pairs (x,y) in the plane that satisfies the equation y = f(x), i.e., {(x, y)| y = f(x), x ∈ X}. It represents a curve in the x, y-plane giving a pictorial representation of the function.

Types of functions

1. An injective or one-to-one function is a function that maps distinct elements of its domain to distinct elements of its codomain, that is, whenever Φ(a₁) = Φ(a₂) then a₁ = a₂. In other words, if we pick any element from the codomain, it is either connected to exactly one or no elements from the domain.

   f, g: ℝ → ℝ, then f(x) = 2x, and g(x) = 2x+1 are both injective, but x² is not, because f(-1) = 1 = f(1). A monotonic function is a function that is either always increasing or always decreasing on its domain. A strictly monotonic function is injective, since in this case x₁ < x₂ implies that f(x₁) < f(x₂) or f(x₁) > f(x₂). e^x is injective because e^x = e^y ⇒ x = y.  

2. A surjective or onto function is loosely speaking a function that “hits everything” or more formally, a function f such that for each element in the codomain there is at least one element in the domain that maps to it. Thus, if we choose any element from the codomain, we can find at least one element from the domain that it is connected to. It is one whose image covers the entire codomain, that is, for every b ∈ B, there exists a ∈ A such that Φ(a) = b (∀b ∈ B, ∃a ∈ A: Φ(a) = b).

   For any set X, the identity function id_X: X → X, id_X(x) = x, ∀ x ∈ X is surjective. f,g: ℝ → ℝ, f(x) = 2x +1 is surjective (∀ y∈ℝ, we have an x(^y-1⁄2) such that f(x)=y), but g(x)=x² is not surjective. However, g: ℝ → ℝ⁺, where ℝ⁺ = {x∈ℝ : x ≥ 0} and g(x)=x² is surjective.

   f: ℝ → ℝ defined by f(x) = $\frac{1}{x^2+1}$ is neither injective (f(1) = f(-1) = $\frac{1}{2}$) nor surjective (there is no element x ∈ ℝ: $\frac{1}{x^2+1}=2↭1=2x^2+2↭x^2=\frac{-1}{2}↭x=\sqrt{\frac{-1}{2}}, x ∈\mathbb{R}$ ⊥).

3. A bijective function is a relation that is both injective and surjective. It is a function that each element in the domain is mapped to exactly one element in the codomain and viceversa. Formally, if Φ(a₁) = Φ(a₂), then a₁ = a₂, and for every b ∈ Y, there exists a ∈ A such that f(a) = b.

   For any set X, the identity function id_X: X → X, id_X(x) = x, ∀ x ∈ X is bijective. Any lineal function over the real numbers, f: ℝ → ℝ, f(x) = ax + b, a ≠ 0 is a bijection. g: ℝ → (^-Π⁄₂, ^Π⁄₂), given by g(x) = arctan(x) is bijective. f: ℝ → ℝ, f(x) = x³ is bijective, too.

Pigeonhole principle

The Pigeonhole principle states that if n items or objects are put into m containers, with n > m, then at least one container must contain more than one item.

Proposition. Suppose that A and B are finite sets and f : A → B is any function. Then,

1. If |A| > |B|, then f is not injective.
2. If |A| < |B|, then f is not surjective.

Problem. Any city containing more than 100,000 people will certainly have at least two people who have the same number of hairs.

Let A be the citizens of a city with more that 100,000 people, B = {0, 1, 2, ···, 100,000}, and h (h stands for hairs or “hairy”): A → B, h(a) = # of hairs of a’s head ⇒ [If |A| > |B|, then f is not injective] h is not injective ⇒ ∃x, y ∈A: h(x) = h(y), so there are two people, x and y, with the same number of hairs∎