Derivatives as Rates of Change II

Perfect is the enemy of the good.

Recall

The derivative of a function at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. It is the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable.

Definition. A function f(x) is differentiable at a point “a” of its domain, if its domain contains an open interval containing “a”, and the limit $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$ exists, f’(a) = L = $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$. More formally, for every positive real number ε, there exists a positive real number δ, such that for every h satisfying 0 < |h| < δ, then |L-$\frac {f(a+h)-f(a)}{h}$|< ε.

1. Power Rule: $\frac{d}{dx}(x^n) = nx^{n-1}$.
2. Sum Rule: $\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))$
3. Product Rule: $\frac{d}{dx}(f(x) \cdot g(x)) = f’(x)g(x) + f(x)g’(x)$.
4. Quotient Rule: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f’(x)g(x) - f(x)g’(x)}{(g(x))^2}$
5. Chain Rule: $\frac{d}{dx}(f(g(x))) = f’(g(x)) \cdot g’(x)$
6. $\frac{d}{dx}(e^x) = e^x, \frac{d}{dx}(\ln(x)) = \frac{1}{x}, \frac{d}{dx}(\sin(x)) = \cos(x), \frac{d}{dx}(\cos(x)) = -\sin(x), \frac{d}{dx}(\tan(x)) = \sec^2(x), \frac{d}{dx}(\arcsin(x)) = \frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arccos(x)) = -\frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arctan(x)) = \frac{1}{1 + x^2}.$

The critical points of a function f are the x-values, within the domain (D) of f for which f’(x) = 0 or where f’ is undefined. Notice that the sign of f’ must stay constant between two consecutive critical points. If the derivative of a function changes sign around a critical point, the function is said to have a local or relative extremum (maximum or minimum) at that point. If f’ changes sign from positive (increasing function) to negative (decreasing function), the function has a local or relative maximum at that critical point. Similarly, if f’ changes sign from negative to positive, the function has a local or relative minimum.

Interpretation

f’(x) is the slope of the line tangent to the graph of f at that particular point (x, f(x)). f’(x) is also the rate of change of the function at x. The average rate of change is the process of calculating the rate at which the output (y-values) changes compared to its input (x-values). This can be visualized as the slope of a secant line passing between two points on a function. In differential calculus, the focus shifts to the instantaneous rate of change, which is found using the derivative of a function.

For example, Growth Rate = $\frac{Births-Deaths}{years}$. The rate of change in population is the derivative of the population function with respect to time, $\frac{dP}{dt}$.

How to solve rates of change problems

You should follow these general steps:

1. Understand the problem, draw a diagram, identify what quantity is changing and with respect to what other quantity(ies).
2. Label all quantities and their rates of change.
3. Relate all quantities in a single equation, that is, use the given information and the problem constraints to set up an equation that relates the quantities involved in the same equation.
4. Differentiate the equation: Calculate the derivative of the equation with respect to the relevant variable to obtain the rate of change.
5. Solve for the unknown: Plug in the known values and solve for the unknown rate of change to answer the question.

Related rates

• During a full-moon night run, an observer with plenty of time and nothing better to do is standing 80 meters away from a long, straight fence when he notices a runner running along it, getting closer to him. What the fork is she doing running so early?, he asked himself. He points her flashlight at him and keeps it on her as she runs. When the distance between him and the runner is 100 meters, he is running at 9 meter per second. At this very moment, at what rate is he turning the flashlight to keep her illuminated.

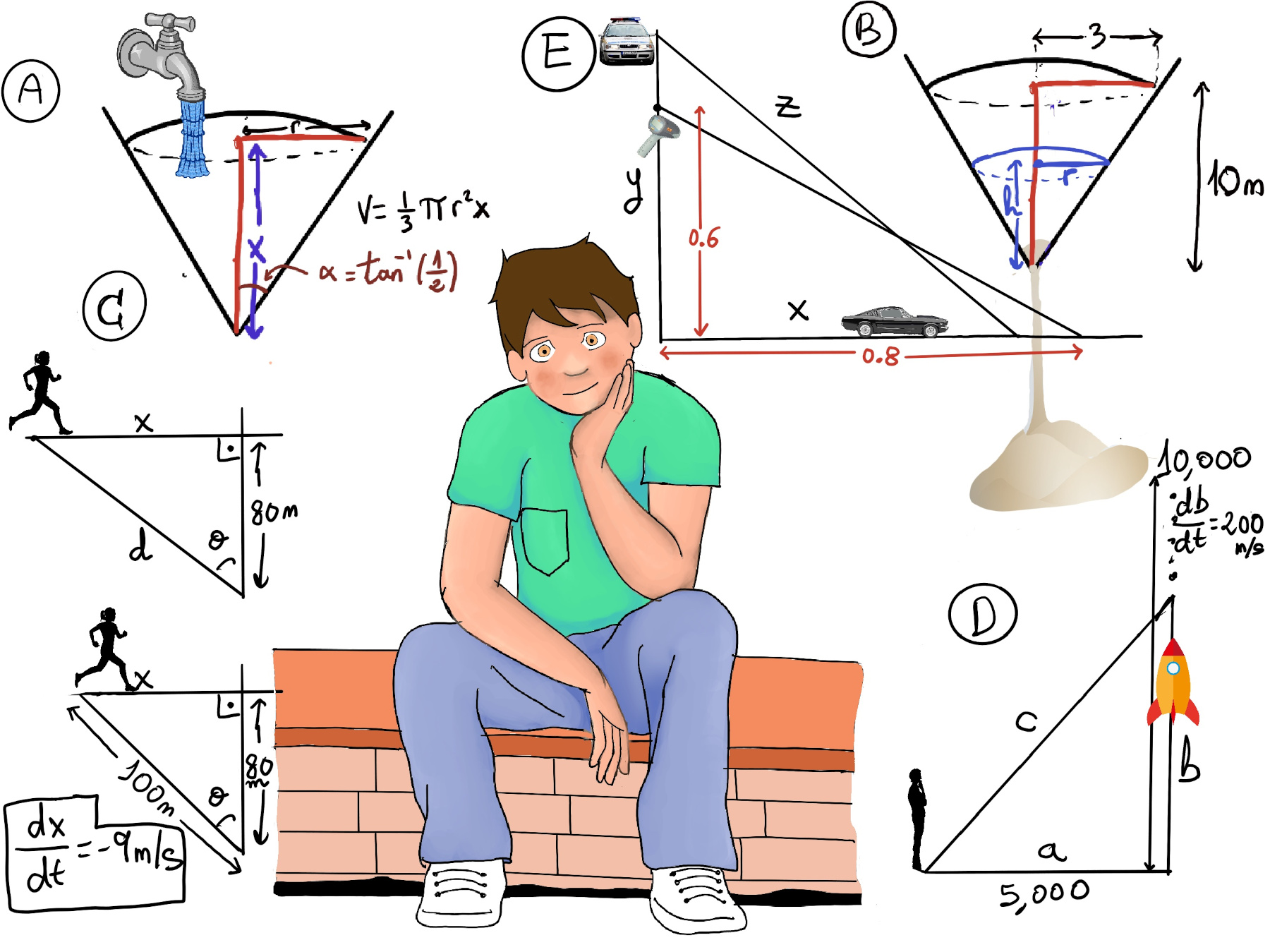
The first step is to fully understand the problem and represent it (Figure C). $\frac{dx}{dt} = -9 m/s$. Goal = $\frac{dθ}{dt}$ at the instant given (when the distance between him and the runner is 100 m.)

Using basic trigonometry, tan(θ) = $\frac{x}{80} ⇒ \frac{d}{dt}(tan(θ)) = \frac{d}{dt}(\frac{x}{80}) ⇒ \frac{d}{dt}(tan(θ)) = \frac{1}{80}\frac{dx}{dt}.$

At this particular time, $\frac{d}{dt}(tan(θ)) = \frac{1}{80}\frac{dx}{dt} = \frac{-9}{80}.$

$\frac{d}{dt}(tan(θ)) = sec^2(θ)\frac{dθ}{dt} = \frac{-9}{80}$. We also know that sec(θ) = $\frac{1}{cos(θ)} = \frac{1}{\frac{80}{100}} = \frac{100}{80} ⇒ \frac{dθ}{dt} = \frac{\frac{-9}{80}}{sec^2(θ)} = \frac{\frac{-9}{80}}{\frac{100^2}{80^2}} = \frac{-9·80}{100^2}$ = -0.072 rad/s.

• A rocket from Elon Musk’s company SpaceX is launched vertically upward from a point 2 miles west of an observer on the ground. What is the speed of the rocket when the angle of elevation of the observer’s line of sight to the rocket is 50° and is increasing at 5° per second?

The first step is to fully understand the problem and represent it (Figure 2.c).

We know that tan(θ)=^h⁄₂ and $\frac{dθ}{dt} = 5° per second$. Goal: $\frac{dh}{dt}~ when~ θ=50°$.  

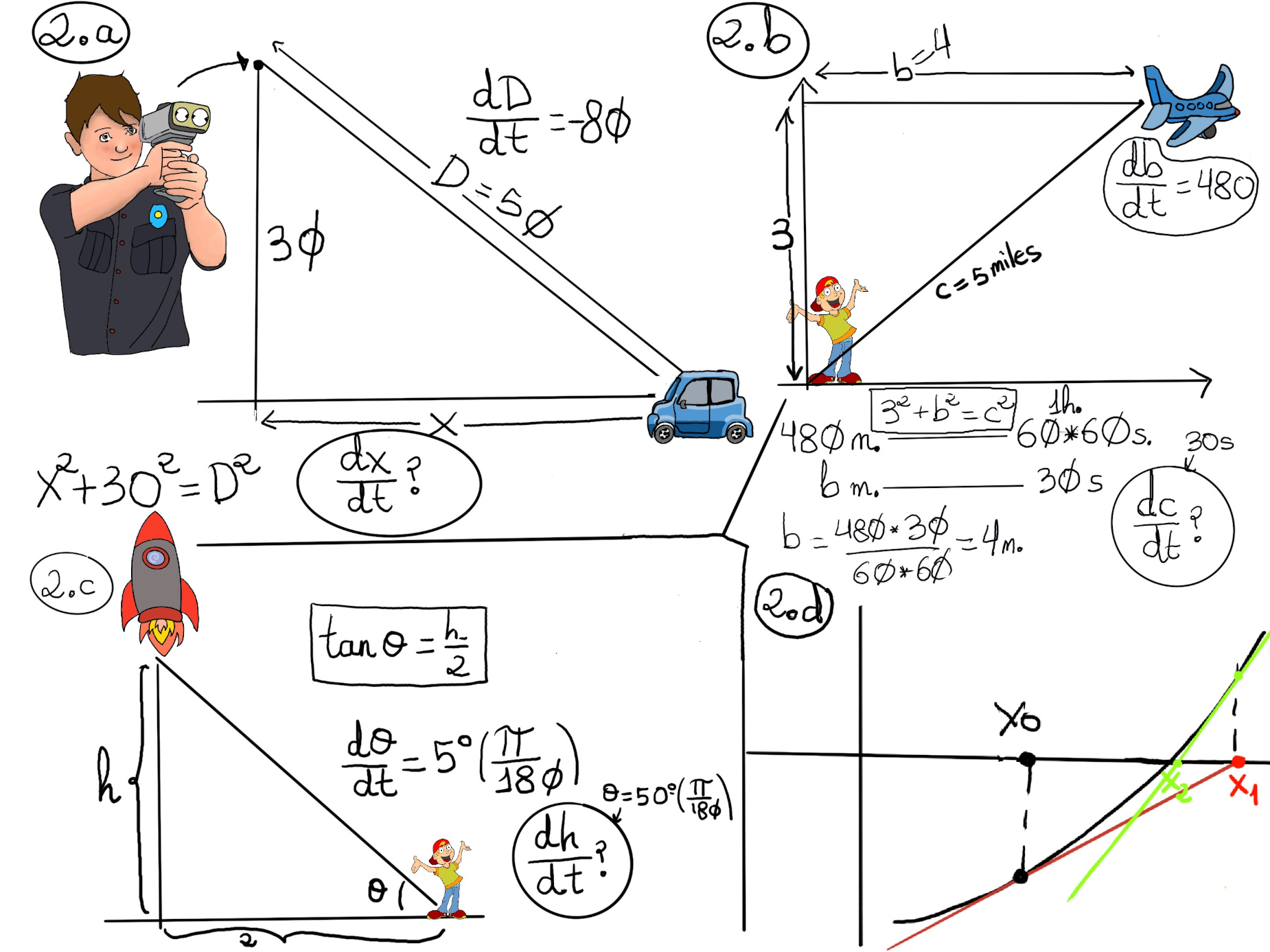
$tan(θ)=\frac{h}{2}$⇒[Let’s differentiate by t] $sec^{2}θ\frac{dθ}{dt} = \frac{1}{2}\frac{dh}{dt}⇒\frac{dh}{dt}=2sec^{2}θ\frac{dθ}{dt}=2·sec^{2}(50°·\frac{\pi}{180})·5°·\frac{\pi}{180} ≈ 0.422mps ≈ 1520.7mph$ -simple conversion mps to mph, 0.422·3.600-

• A block of ice in the form of a cube with each side of length x meters melts at a rate of 9.72 m³ per seconds because of global warming -so pay more taxes for the climate! Assume that the block retains its cube shape as it melts. Find the rate of change of x or how fast is the side shrinking at the instant when x = 12 m.

V = x³, we know that $\frac{dV}{dt} = -9.72m^3$ our goal is $\frac{dx}{dt}\bigg|_{x=12}$

$\frac{dV}{dx} = 3x^2, -9.72 = \frac{dV}{dt} = \frac{dV}{dx}·\frac{dx}{dt} = 3x^2·\frac{dx}{dt} ⇒ \frac{dx}{dt} = \frac{-9.72}{3x^2}$

$\frac{dx}{dt}\bigg|_{x=12} = \frac{-9.72}{3·12^2} = -0.0225 m/s$

• A container is in the form of a right circular cone where α = $tan^{-1}(\frac{1}{2})$. Initially, the container is empty, then water is added at a constant rate of 14 cubic meters per minute. The inverted cone has a depth of x meters. Find the rate at which x is increasing at the instant when x is 8m (Figure A).

$\frac{dV}{dt} = 14$, α = $tan^{-1}(\frac{1}{2}) ↭ tan(α) = \frac{1}{2} = \frac{r}{x} ⇒ r = \frac{x}{2}$

V = $\frac{1}{3}π·r^2·x = \frac{1}{3}π·(\frac{x}{2})^2·x = \frac{1}{12}·π·x^3 ⇒ \frac{dV}{dx} = π·\frac{1}{4}·x^2 ⇒ \frac{dx}{dV} = \frac{4}{π·x^2} ⇒ \frac{dx}{dt} = \frac{dx}{dV}·\frac{dV}{dt} = \frac{4}{π·x^2}·14, \frac{dx}{dt}\bigg|_{x = 8} = \frac{4}{π·8^2}·14 ≈ 0.28 m/s.$

• Police are 30 feet from the side of the road and they are given a strick quota of writing one ticket per day. Their radar sees your car approaching at 80 feet per second when your car is 50 feet away from the radar gun. The speed limit is 65 miles per hour, police are salivating already. Are you speeding?

The diagram is shown in Figure 2.a. By the Pythagorean theorem (we can never thank him enough), x²+30²=D² (Initially, D = 50 ⇒ x =$\sqrt{50^2-30^2}$ = 40) and $\frac{dD}{dt}=-80.$ Goal: $\frac{dx}{dt}?$

x²+30²=D² ⇒ $2x\frac{dx}{dt} = 2D\frac{dD}{dt}$

Now, we can plug the values in the previous equation, $2x\frac{dx}{dt} = 2D\frac{dD}{dt} ⇒ 2·40·\frac{dx}{dt} = 2·50·(-80) ⇒ \frac{dx}{dt} = -100 ft/sec.$

|-100 ft/sec| > 95 ft/sec = 65mph. Yes, you are speeding 🚗, but not for much.

• The population of a city is tripling every 5 years. If its current population is 10,000, what will be its approximate population 2 years from now?

Let P(t) be the population of a city t years from now (we are going to be using thousands as unit). P’(0) -the current growth rate- ≈ $\frac{P(5)-P(0)}{5 -0} = \frac{30-10}{5} = 4.$

For small values of h (in other words, being relatively close to a), f’(a) ≈ $\frac{f(a+h)-f(a)}{h}↭ f(a+h) ≈ f(a) + f’(a)h$ (this is the Linear approximation of a function). In our particular case, a = 0, h = 2, P(2) ≈ P(0) + P’(0)·2 = 10 + 4·2 = 18 ⇒ 18,000 will be the population of the city in two years.

• A cone with a height of 10 m and a base radius of 3m is held vertex down. It is filled with sand. A hole in the bottom of the cone allows the sand to escape at a rate of 0.5 m³/s. Find the rate at which the depth is decreasing when the depth is 2m.

Figure B. Let h be the height of the sand. Recall that similar triangles have the same corresponding angle measures and proportional side lengths ⇒ $\frac{r}{h} = \frac{3}{10} ⇒ r = \frac{3}{10}·h$ (i)

$\frac{dV}{dt} = -0.5, V = \frac{1}{3}π·r^2·h$

V = $\frac{1}{3}π·r^2·h =$[Replacing r by (i)] $\frac{1}{3}π·(\frac{3}{10}·h)^2·h = \frac{3π}{100}h^3 ⇒ \frac{dV}{dh} = \frac{9π}{100}h^2 ⇒ \frac{dh}{dV} = \frac{100}{9πh^2}$

$\frac{dh}{dt} = \frac{dh}{dV}·\frac{dV}{dt} = \frac{100}{9πh^2}·-0.5 = \frac{-50}{9πh^2} ⇒ \frac{dh}{dt}\bigg|_{h=2} = \frac{-50}{9π4} = \frac{-25}{18π}$≈ -0.44 m/s.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.