Normal Subgroups II

“Some drink at the fountain of knowledge. Others just gargle. You are just a moron stuck to a nose,” I retorted, but my imagination kept running wild, “You do not have a nose, a superlative muzzle owns you, a crooked sundial casting a disproportionate shadow, an elephant dying a terrible death, face up, gasping from breath; the Great Pyramid of Giza or more accurate, all Egyptian pyramids pile together; the king of swordfish, an insult to nature, and a joke to many,” Anawim, Apocalypse, #justtothepoint.

Recall

Definition. A subgroup H of a group G, H ≤ G, is called a normal subgroup of G if aH = Ha, ∀a ∈ G. That is, a normal subgroup of a group G is one in which the right and left cosets are precisely the same. The usual notation for this relation is H ◁ G. It means ∀a ∈ G, h ∈ H, ∃h’, h’’∈ H: ah = h’a and ha = ah’’.

Normal Subgroup Test or alternative definition. A subgroup H of a group G is normal in G if and only if is invariant under conjugation by members of the group G. H ◁ G iff gHg^-1 ⊆ H, ∀g ∈ G, i.e., ∀g ∈ G, h ∈ H, ghg^-1 ∈ H.

More examples

• Let G = ℤ₈ = {0, 1, 2, 3, 4, 5, 6, 7}, and let H be the subgroup {0, 4} ◁ G. G/H = {H, 1 + H, 2 + H, 3 + H}.

To calculate (2 + H) + (3 + H), let’s take two representatives 2 + 7 = 9 =_{mod 8} 1 ∈ 1 + H ⇒ (2 + H) + (3 + H) = 1 + H. There are only two groups of order 4, namely ℤ₄ (cyclic) and ℤ₂ x ℤ₂. Besides,

1. G/H = ⟨1 + H⟩, cyclic, hence G/H ≋ ℤ₄.
2. Replace H = {0, 4} with 0, 1 + H = {1, 5} with 1, 2 + H = {2, 6} with 2, 3 + H = {3, 7} with 3.

• Let G = ℤ₄ x ℤ₄, H = ⟨(1, 3)⟩, ℤ₄ x ℤ₄/⟨(1, 3)⟩ = {⟨(1, 3)⟩, (0, 1) + ⟨(1, 3)⟩, (0, 2) + ⟨(1, 3)⟩, (0, 3) + ⟨(1, 3)⟩} where
  H = ⟨(1, 3)⟩ = {(0, 0), (1, 3), (2, 2), (3, 1)}
  (0, 1) + ⟨(1, 3)⟩ = {(0, 1), (1, 0), (2, 3), (3, 2)}
  (0, 2) + ⟨(1, 3)⟩ = {(0, 2), (1, 1), (2, 0), (3, 3)}
  (0, 3) + ⟨(1, 3)⟩ = {(0, 3), (1, 2), (2, 1), (3, 0)}

Some calculations: (1, 3) + (1, 3) = (2, 6_{mod 4}) = (2, 2); 3·(1, 3) = (3, 1); 4·(1, 3) = (0, 0) ⇒ H = ⟨(1, 3)⟩ = {(0, 0), (1, 3), (2, 2), (3, 1)}.

Let’s add cosets, e.g., (0, 2) + ⟨(1, 3)⟩ + (0, 1) + ⟨(1, 3)⟩ =[Let’s select two representatives] (0, 2) + (0, 1) + ⟨(1, 3)⟩ = (0, 3) + ⟨(1, 3)⟩

Futhermore, the coset |(0, 1) + ⟨(1, 3)⟩| = 4 ⇒ ℤ₄ x ℤ₄/⟨(1, 3)⟩ = {⟨(1, 3)⟩, (0, 1) + ⟨(1, 3)⟩, (0, 2) + ⟨(1, 3)⟩, (0, 3) + ⟨(1, 3)⟩} ≋ ℤ₄

• Let G = ℤ₄ x ℤ₈, and H = ⟨(0, 1)⟩ = {(0, 0), (0, 1), (0, 2), . . . , (0, 7)}. |G : H| = 4·8/4 = 4 ⇒ G/H ≋ ℤ₄ or ℤ₂ x ℤ₂.

(x, y) + H = (v, w) + H ↭ (x, y) - (v, w) = (x - v, y -w) ∈ H ↭ x = v ⇒[Each coset contains a unique element (x, 0) where x ∈ ℤ₄)] G/H = {H, (1, 0) + H, (2, 0) + H, (3, 0) + H}. G/H = {H, (1, 0) + H, (2, 0) + H, (3, 0) + H} ≋ ℤ₄ because there is an isomorphism Φ: ℤ₄ → G/H, x → (x, 0) + H or, alternatively, we can easily check that |(1, 0) + H | = 4, then G/H = ⟨(1, 0) + H⟩

• Let G = A₄ the alternating group of even permutations of S₄ = {() -α₁ = 1-,(12)(34) -α₂ = 2-, (13)(24) -α₃ = 3-,(14)(23) -4-,(123) -5-, (243)-6-, (142) -7-, (134) -8-, (132) -9, (143) -10-,(234) -11-, (124) -12-}. Let H = {α₁, α₂, α₃, α₄} = {(), (12)(34), (13)(24), (14)(23)}, H ◁ A₄.

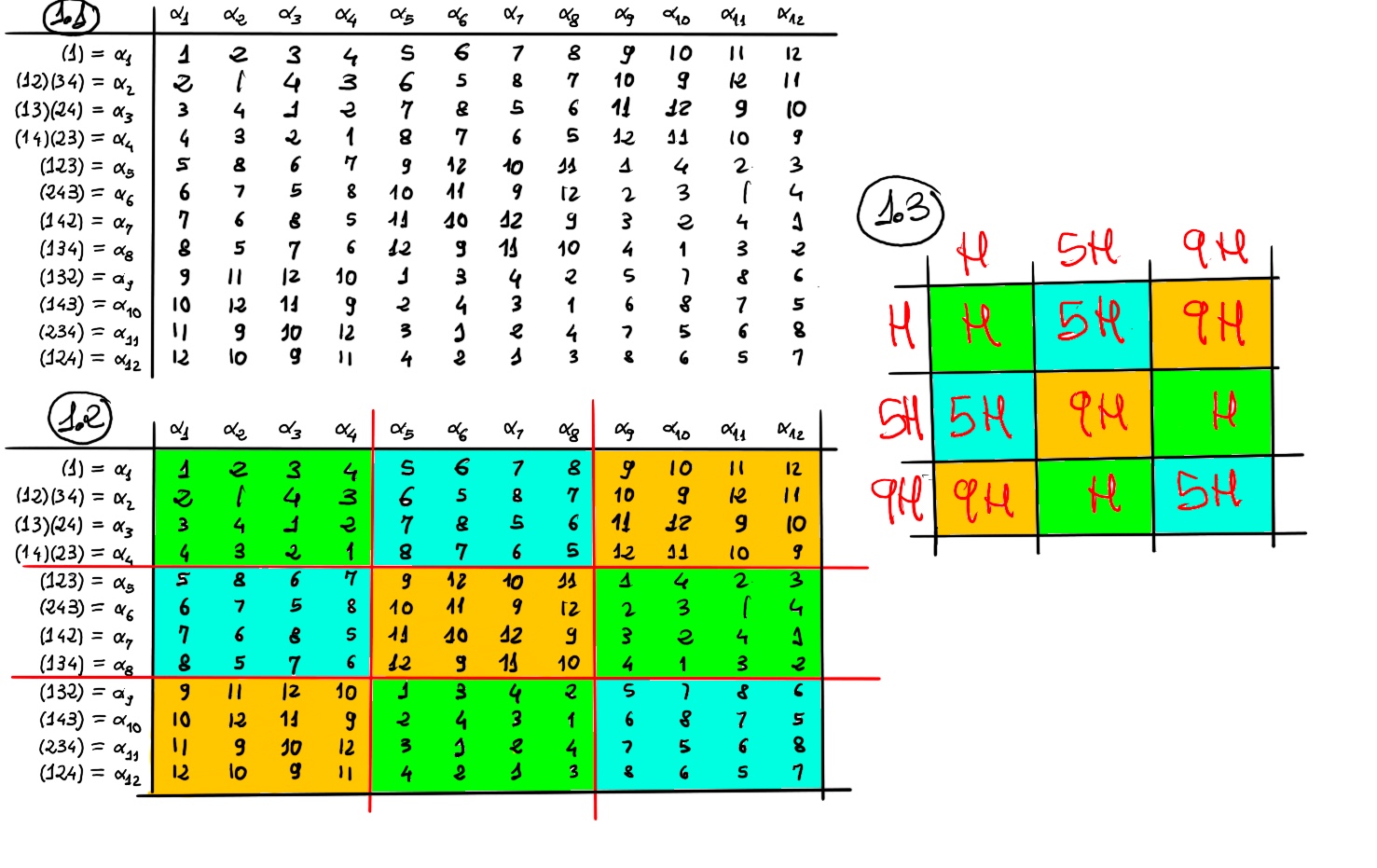
The cosets of H are: H; 5H = {α₅, α₆, α₇, α₈}, α₅α₁ = α₅; α₅α₂ = (123)(12)(34) = (134) = α₈; α₅α₃ = (123)(13)(24) = (243) = α₆; α₅α₄ = (123)(14)(23) = (142) = α₇. Analogously, 9H = {α₉, α₁₀, α₁₁, α₁₂}. Example: (α₅α₁)·(α₉α₁) = (123)()(132)() = () ⇒ 5H·9H = H, (α₅α₁)·(α₅α₁) = (123)()(123)() = (132)() ⇒ 5H·5H = 9H, and so on.

We normally use e = () for simplicity’s sake. (α₅α₂)·(α₉α₃) = (123)(12)(34)(132)(13)(24) = (12)(34) = α₂ ⇒ 5H·9H = H

• Let G = U(9) = {1, 2, 4, 5, 7, 8}. N = {1, 8}, N ◁ G. |G/N| = |G|/|N| = 6/2 = 3. G/N = {N, 2N, 4N} ≋ ℤ₃ where 2N = {2, 7} and 4N = {4, 5}.

2N = {2·1_{mod 9}, 2·8_{mod 9}} = {2, 16_{mod 9}} = {2, 7}, 4N = {4·1_{mod 9}, 4·8_{mod 9}} = {4, 32_{mod 9}} = {4, 5}, 2·5 = 10_{mod 9} = 1 ⇒ 2N·4N = N.

• Let U(20) = {1, 3, 7, 9, 11, 13, 17, 19} be the group of units in ℤ₂₀. Consider the subgroup H = {1, 19}. U(20)/H = {H, 3H, 7H, 19H}, |U(20)/H| = |U(20)|/|H| = 8/2 = 4 where 3H = {3, 17}, 7H = {7, 13}, and 9H = {9, 11}

3H = {3·1_{mod 20}, 3·19_{mod 20}} = {3, 57_{mod 20}} = {3, 17}, 7N = {7·1_{mod 20}, 7·19_{mod 20}} = {7, 133_{mod 20}} = {7, 13}, 3·7 = 21_{mod 20} = 1 ⇒ 3H·7H = H.

|3H| = 4 ⇒ U(20)/H = ⟨3H⟩ ≋ ℤ₄

• Let G = U(30) = {1, 7, 11, 13, 17, 19, 23, 29}, H = {1, 29}, H ◁ G, |G/H| = |G|/|H| = 4. G/H = {H, 7H, 11H, 17H} = ⟨7H⟩ where 1H = 29H = {1, 29} = H1 = H29. 11H = 19H = {11, 19} = H11 = H19. 7H = 23H = {7, 23} = H7 = H23. 13H = 17H = {13, 17} = H13 = H17.

  7·7 = 49 =₃₀ 19 ⇒ (7H)² = 11H = {11, 19}. 7·7·7 = 343 =₃₀ 13 ⇒ (7H)³ = 13H. 7·7·7·7 = 2401 =₃₀ 1 ⇒ (7H)⁴ = H ⇒ |7H| = 4 ⇒ G/H = ⟨7H⟩ ⇒ G/H ≋ ℤ₄

• Let G = U(32) = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31}, H = {1, 17}. Then, G/H is an Abelian group of order |G|/|H| = 16/2 = 8 ⇒ G is isomorphic to one of the following groups ℤ₈, ℤ₄ ⊕ ℤ₂, or ℤ₂ ⊕ ℤ₂ ⊕ ℤ₂.

G/H = {1H, 3H, 5H, 7H, 9H, 11H, 13H, 15H} where 1H = {1, 17}, 3H = {3·1, 3·17 = 51_{mod 32} 19} = {3, 19}, 5H = {5·1, 5·17 = 85_{mod 32} 21} = {5, 21}, 7H = {7, 23}, 9H = {9, 25}, 11H = {11, 27}, 13H = {13, 29}, 15H = {15, 31}

(3H)² = (3H)·(3H) = 9H ≠ H, (3H)⁴ = H (3·3·3·3 = 81 = 17 (mod 32)) ⇒ |3H| = 4 and ℤ₂ ⊕ ℤ₂ ⊕ ℤ₂ has no elements of order 4 ⇒ G/H ≇ ℤ₂ ⊕ ℤ₂ ⊕ ℤ₂. Since |7H| = |9H| = 2 (7·7 = 49_{mod 32} = 17, 9·9 = 81_{mod 32} = 17) ⇒ G/H has at least two elements of order 2, but ℤ₈ has only one element of order 2, namely 4 ⇒ G/H ≇ ℤ₈, hence G/H ≋ ℤ₄ ⊕ ℤ₂

• Let G = U(32) = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31}, K = {1, 15} ⇒ |G/K| = |G|/|K| = 16/2 = 8 ⇒ G is isomorphic to one of the following groups ℤ₈, ℤ₄ ⊕ ℤ₂, or ℤ₂ ⊕ ℤ₂ ⊕ ℤ₂. The cosets are: K, 3K = {3, 13}, 5K = {5, 11}, 7K = {7, 9}, 17K = {17, 31}, 19K = {19, 29}, 21K = {21, 27}, and 23K = {23, 25}.

Which of the three Abelian groups of order eight is it? (3K)² = 9K, (3K)³ =[3·3·3_{mod 43} = 27] = 21K. (3K)⁴ =[27*3 = 81_{mod 32} = 17] 17K ≠ K ⇒[|G/K| = 8, and so by Lagrange Theorem, the only options are 1, 2, 4 and 8] |3K| = 8 ⇒[G/K is cyclic] G/K ≋ ℤ₈.

• The quaternion group Q₈ is a non-Abelian group of order eight. ⟨i⟩ = {1, i, -1, -i} ◁ Q₈. |Q₈/⟨i⟩| = |Q₈|/|⟨i⟩| = 8/4 = 2. Q₈/⟨i⟩ = {⟨i⟩, j⟨i⟩} where j⟨i⟩ = {j, ji, -j, j(-i)} = {j, -k, -j, k}.

Let’s see the cosets of the group, Q₈/⟨i⟩ = {⟨i⟩, j⟨i⟩}. Notice that ⟨i⟩ is the identity of the quotient group. The Cayley table for Q₈/⟨i⟩ is exactly equal as ℤ₂, and therefore Q₈/⟨i⟩ ≋ ℤ₂. The same applies with ⟨j⟩ and ⟨k⟩. Figures 1.c. and 1.d.

• The center of the group is Z(Q₈) = ⟨-1⟩ = {-1, 1}, then ⟨-1⟩ ◁ Q₈. |Q₈/⟨-1⟩| = |Q₈|/|⟨-1⟩| = 8/2 = 4.

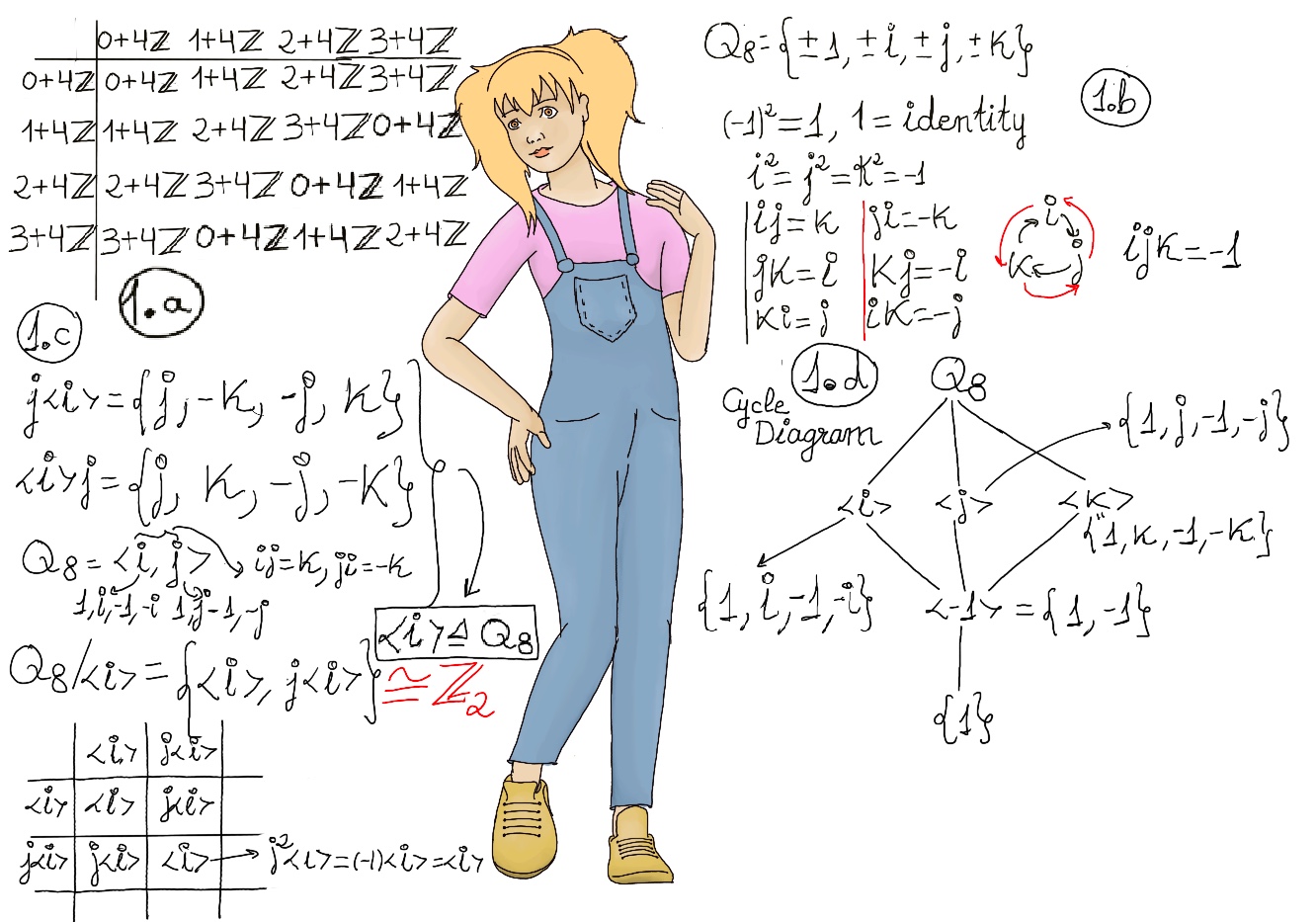
Q₈/⟨-1⟩ = {⟨-1⟩, i⟨-1⟩, j⟨-1⟩, k⟨-1⟩} and all elements of this group has order 2 except obviously the identity, that’s why Q₈/⟨-1⟩ is isomorphic to ℤ₂ x ℤ₂.

⟨-1⟩ = {-1, 1}, i⟨-1⟩ = {-i, i}, i⟨-1⟩i⟨-1⟩ = i²⟨-1⟩ = -1⟨-1⟩ =[-1 ∈ ⟨-1⟩] ⟨-1⟩

The isomorphism Q₈/⟨-1⟩ → ℤ₂ x ℤ₂, is defined by ⟨-1⟩ → (0, 0), i⟨-1⟩ → (1, 0), j⟨-1⟩ → (0, 1), k⟨-1⟩ → (1, 1).

• Consider A₄, the alternating group on 4 letters. A₄ = {(1), (12)(34), (13)(24), (14)(23), (123), (132), (124), (142), (134), (143), (234),(243)}. A₄ has no subgroups of order 6.

Let’s suppose H ≤ G, |H| = 6, then |A₄/H| = 12/2 = 2 ⇒ [Let H ≤ G be any subgroup of a finite group G. If |G/H| = |G|/|H|=2 then H ◁ G.] H ◁ G.

|H| = 6, so there are some 3-cycle (there are 8 3-cycles) that are not in H. Let x be a 3-cycle that is not in H, and consider the cosets H, xH, and x²H in A₄/H -x³H =[x is a 3-cycle] eH = H-. Since this is a group of order 2, two of the cosets must be equal. However, H and xH are distinct by construction (x ∉ H ↭ xH ≠ H), so we have two options:

1. H = x²H ⇒ [x³ = 1 as x is a 3-cycle, x² = x^-1 && aH = a iff a ∈ H] x² = x^-1 ∈ H ⇒ [H ≤ G, H is closed under inverses as a subgroup] x ∈ H ⊥
2. xH = x²H ⇒ H = x^-1x²H = xH ⇒ x ∈ H ⊥

Theorem. Let G be a group, and let be Z(G) the center of G. If G/Z(G) is cyclic, then G is Abelian.

Proof:

Let gZ(G) be a generator of the cyclic group G/Z(G), ⟨gZ(G)⟩ = G/Z(G)

∀a, b ∈ G, ∃i, j ∈ ℤ: aZ(G) = (gZ(G))ⁱ = [(aH)(bH)=abH by definition] gⁱZ(G), and bZ(G) = (gZ(G))^j = [(aH)(bH)=abH by definition] g^jZ(G)

aZ(G) = gⁱZ(G), bZ(G) = g^jZ(G) ⇒ [A left (or right) coset is uniquely determined or represented by any one of its elements, i.e., aH = bH iff a ∈ bH] a ∈ gⁱZ(G), b ∈ g^jZ(G) ⇒ ∃ x, y ∈ Z(G): a = gⁱx, b = g^jy

ab = (gⁱx)(g^jy) =[Associativity] gⁱ(xg^j)y [x ∈ Z(G) ⇒ xg^j = g^jx] gⁱ(g^jx)y = (gⁱg^j)(xy) =[Trivial exponential rules] (g^jgⁱ)(xy) =[x ∈ Z(G)] (g^jgⁱ)(yx) = g^j(gⁱy)x =[y ∈ Z(G)] (g^jy)(gⁱx) = ba ∎

Corollary 1: If G/H is cyclic, H ≤ Z(G) ⇒ G is Abelian.

Proof.

H ≤ Z(G), G/H cyclic ⇒[Claim 🔑] G/Z(G) cyclic ⇒[By the previous theorem] G is Abelian.

Claim 🔑: H ≤ Z(G), G/H cyclic ⇒ G/Z(G) cyclic.

G/H cyclic ⇒ G/H = ⟨aH⟩ ⇒ ∀g ∈ G, ∃n ∈ ℤ: gH = (aH)ⁿ = aⁿH ↭[aH = bH ↭ b^-1a ∈ H] g^-1aⁿ ∈ H ≤ Z(G) ⇒ g^-1aⁿ ∈ Z(G) ↭ gZ(G) = aⁿZ(G) = (aZ(G))ⁿ, so aZ(G) is a generator or G/Z(G)∎

Corollary 2: If G is non-Abelian, then G/Z(G) is not cyclic.

Corollary 3: Let G be a non-Abelian group, |G| = pq, where p and q are primes, then G must have a trivial center.

Proof: Let G be a non-Abelian group ⇒ G/Z(G) is not cyclic.

Z(G) is a normal subgroup of G (Z(G) ◁ G) ⇒[|Z(G)| divides |G| = p·q, p and q are primes] |Z(G)| = 1, p, q or pq.

G is not Abelian ⇒ |Z(G)| ≠ pq. If |Z(G)| = p or q, then |G/Z(G)| is either q or p. Since p and q are primes ⇒ [Every group of prime order is cyclic.] G/Z(G) is a cyclic group ⊥ (G is non-Abelian group, Corollary 2). Therefore, |Z(G)| = 1, G has a trivial center∎

A group of prime order is always cyclic. Let G be a non-trivial group, where |G| is prime. In other words, it has an element g ≠ e, |g| ≠ 1, |g| divides |G| prime ⇒ |g| = |G|, and therefore, G = ⟨g⟩.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.