|
 |
 |
|
 |
“You will not feel pain, but pressure during labour,” Susanne was thinking about his childbirth’s instructor words. “An insufferable know-it-all midwife, this was as accurate as saying that a tornado is an air current,” Apocalypse, Anawim, #justtothepoint.
Definition. A tetrahedron is a polyhedron composed of four triangular faces, six straight edges, and four vertices in a three-dimensional space. A regular tetrahedron is a tetrahedron having equilateral triangles as faces. It is one of the five regular Platonic solids, which have been known since antiquity.
There are two types of symmetries: reflections (e.g., reflections in a plane perpendicular to an edge) and rotations.
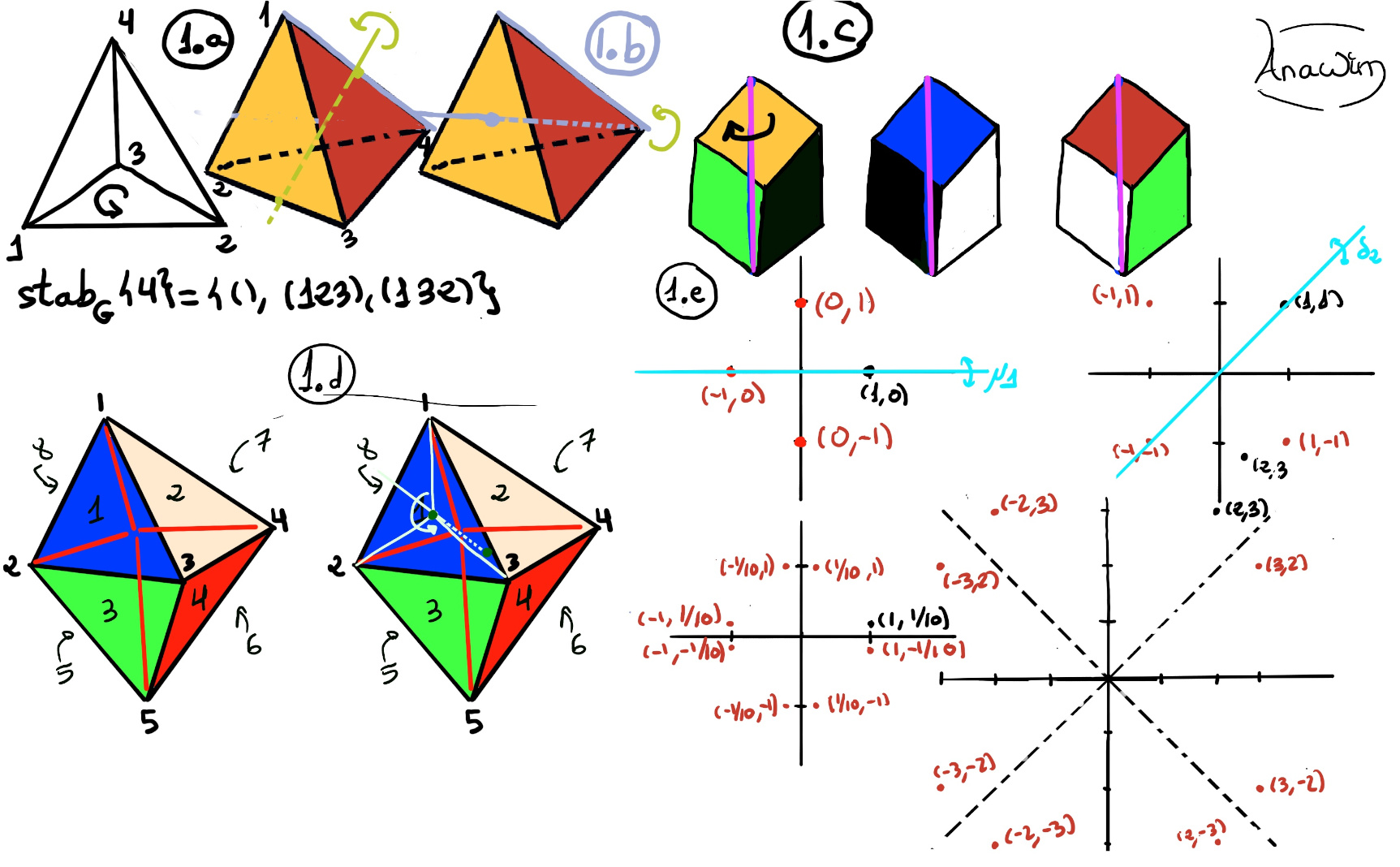
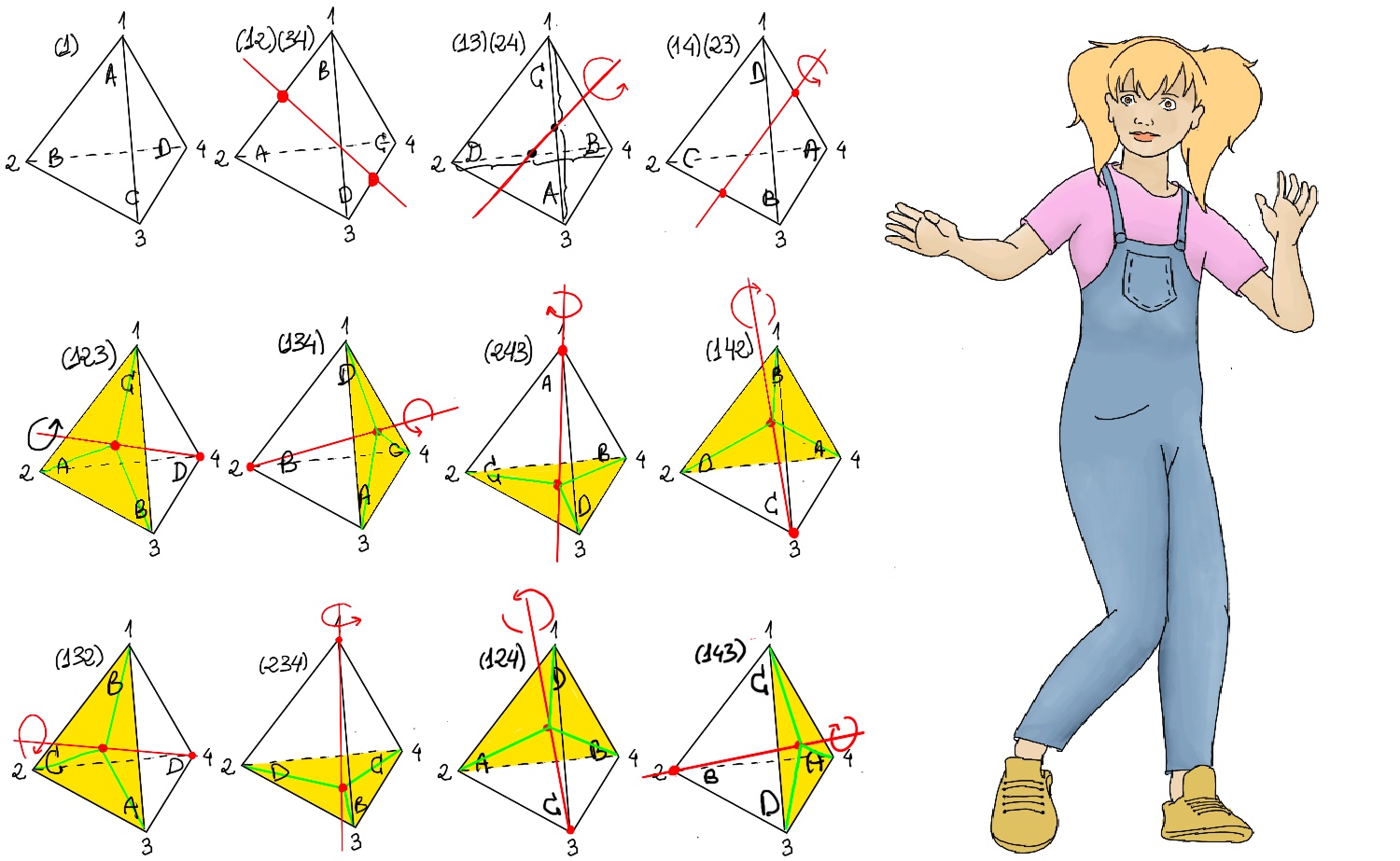
Let G = A4 the alternating group of even permutations of S4 = {(1) -1-,(12) (34) -2-, (13)(24) -3-,(14)(23) -4-,(123) -5-, (243)-6-, (142) -7-, (134) -8-, (132) -9, (143) -10-,(234) -11-, (124) -12-}.
Let V be the set of vertices of the regular tetrahedron. Labelling the vertices, we obtain a bijection V ≋ {1, 2, 3, 4}. The action of the tetrahedral group on V is encoded in an injective map T → Bij(V, V) ≋ S4. Indeed, any symmetry of the tetrahedron is uniquely determined by its effect on V, hence one-to-one.
Theorem. The group of rotational symmetries of a tetrahedron is isomorphic to the alternating group of even permutations on four elements, A4.
Let S be a finite set. The alternating group on S is defined as the group of all even permutations on S under composition. An even permutation is a permutation whose cycle decomposition has an even number of cycles of even size. In other words, it can be written or expressed as a product of an even number of transpositions.
The A4 multiplication table is given in Table 1.1. The rotations by 180° together with the identity form a normal subgroup. Let H = {α1, α2, α3, α4} = {(), (12)(34), (13)(24), (14)(23)}.
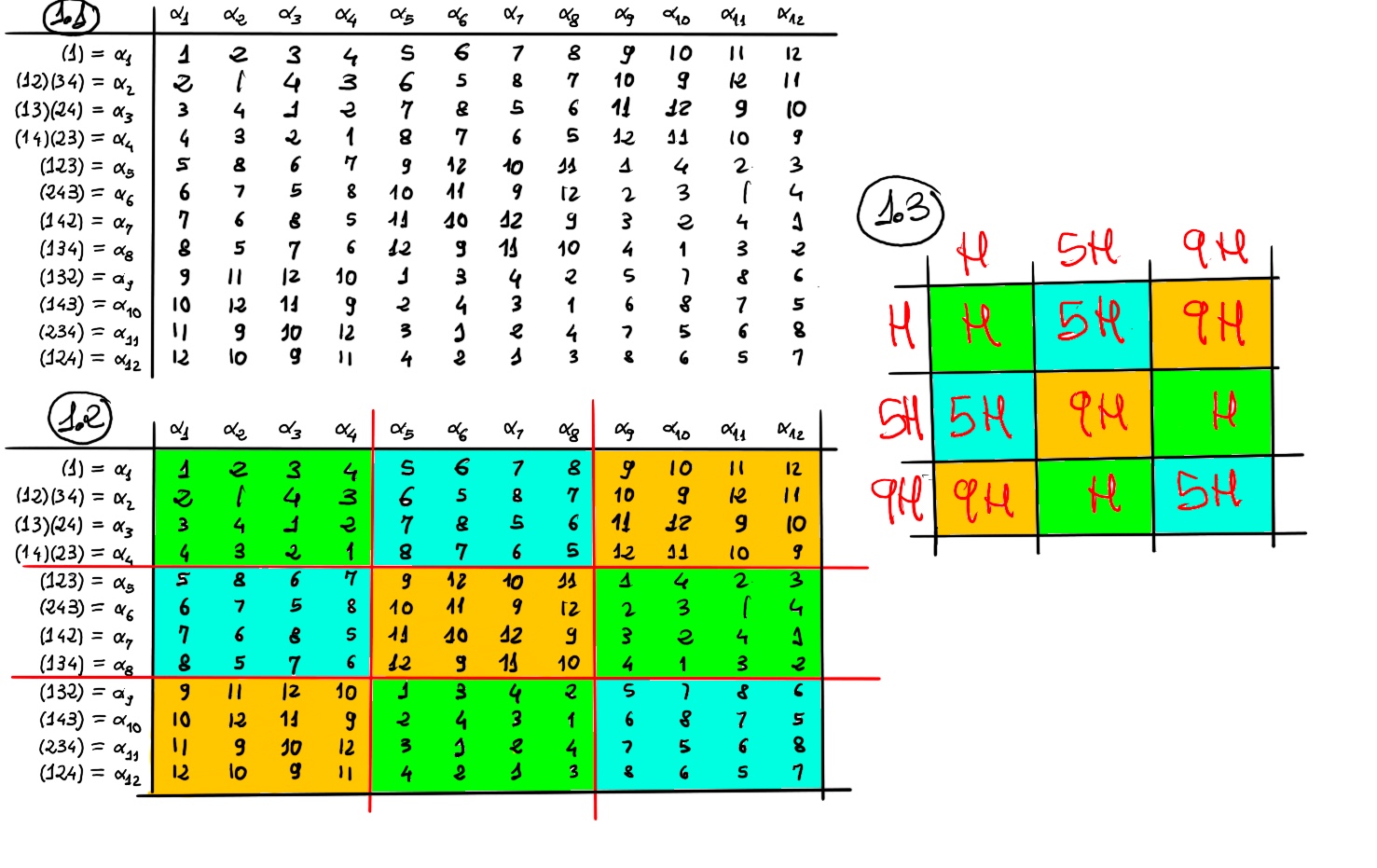
H = (1)H = (12)(34)H = (13)(24)H = (14)(23)H = H(1) = H(12)(34) = H(13)(24) = H(14)(23)
(123)H = (134)H = (243)H = (142)H = H(123) = H(134) = H(243) = H(142)
(132)H = (234)H = (124)H = (143)H = H(132) = H(234) = H(124) = H(143). Therefore, H ◁ A4.
Besides, we can obtain the Cayley table for G/H = {H, 5H, 9H} (Table 1.3.). |A4/H| = |A4|/|H| = 12/4 = 3, and since there is only 1 group of order 3 (up to isomorphism), A4/H ≋ ℤ3 Observe that the multiplication table for A4 can be simplified into small boxes that are cosets of H. We can represent an entire box by a single element of the box!

A regular tetrahedron has 12 rotational (or orientation-preserving) symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation. The group of all symmetries is isomorphic to the group S4, the symmetric group of permutations of four objects.
Orbit-Stabilizer Theorem. Let G be a finite group of permutations of a set S. Then, ∀i ∈ S, |orbG(i)| = [G: stabG(i)] = $\frac{|G|}{|Stab(x)|}$ or, alternatively, |G| = |orbG(i)||stabG(i)|
A tetrahedron is a pyramid with a triangular base. It has 4 vertices, 6 edges, and 4 faces. Clearly any vertex can be rotated to any other, orbG(v1) = {v1, v2, v3, v4} The stabilizer of the vertex 1 is the group of rotations keeping it fixed. It consists of the identity e, and (234), and (243) (Figure 1.a.). Any rotational axis going through a vertex and the centre of gravity must go through the centre of the opposite face which is an equilateral and the angle of rotation that leaves the vertex invariant is 2π/3. G = A4 = {(), (123), (124), (132), (134), (143), (124), (234), (243), (12)(34), (13)(24), (14)(23)}
The edge |orbG(23)| = 6, and |stabG(23)| = 2, the identity and the axe joining the midpoint of (23) and (14), that is “e” and “(14)(23)”.
| Action | #orbitG | #stabG | ord(G) | |
|---|---|---|---|---|
| on faces | 4 | 3 | 12 | |
| on edges | 6 | 2 (Figure 1.b) | 12 | |
| on vertices | 4 | 3 | 12 |
The group of rotational symmetries in ℝ3 leaving the tetrahedron invariant are: the identity, I; two rotations through 120° and 240° about each of the four axes joining vertices with centres of opposite faces; and one rotation through angle 180° about each of the three axes joining the midpoints of opposites edges.