Strategy in finding limits

“If you dream it you can do it” is absolutely and undeniably bullshit, wretched crap of the worst order. What cannot be cannot be, and besides witch, it’s impossible. If you can make money at what you love to do, excellent. If you cannot, understand reality, tame your dreams, search for a career path close enough to your passion, based on your education, experience, personality, talents, and skills, but still realistic and achievable, JustToThePoint, Anawim, #justtothepoint.

Recall

Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).

The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ. A mathematical function is like a black box that takes certain input values and generates corresponding output values (Figure E).

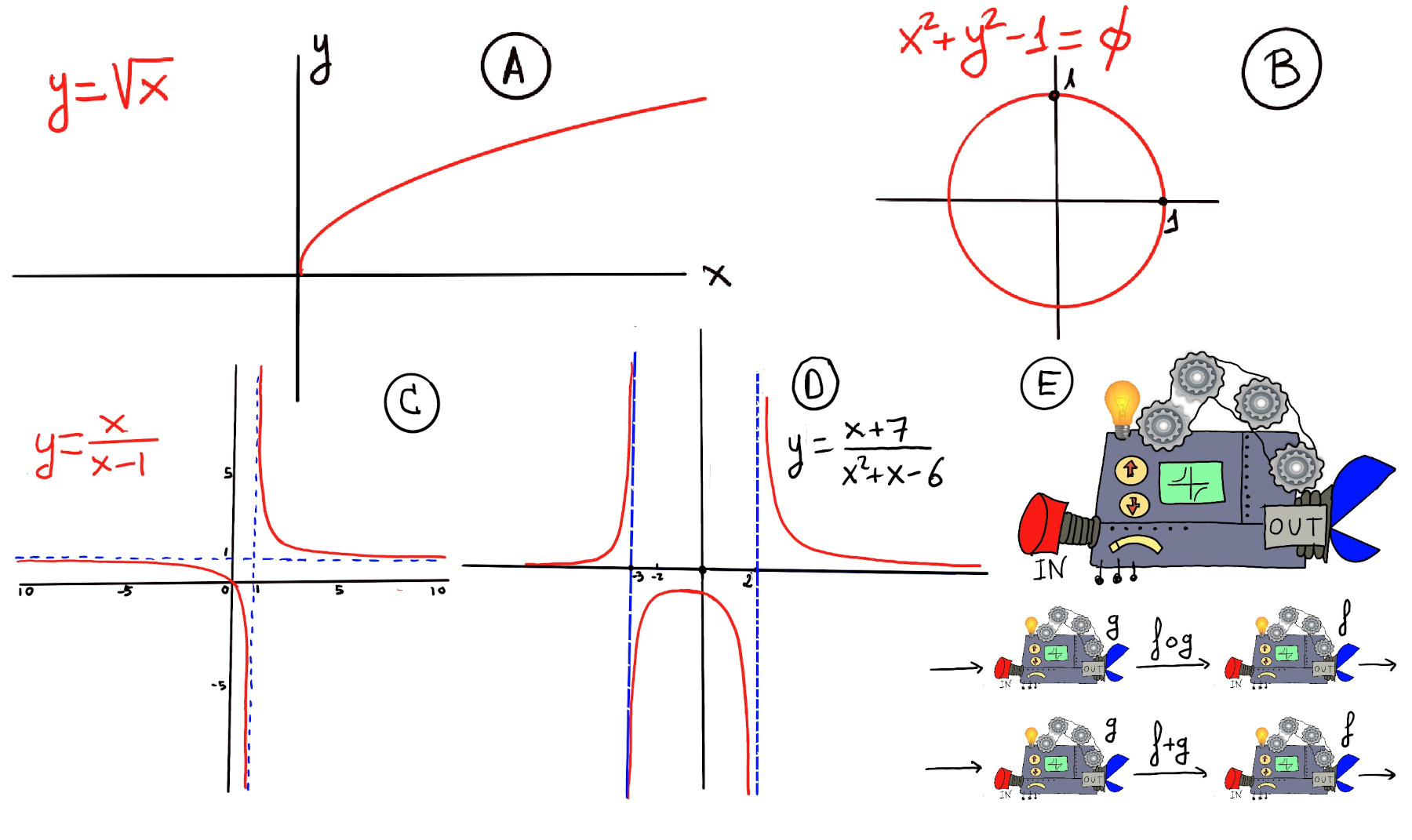
Very loosing speaking, a limit is the value to which a function grows close as the input get closer and closer to some other given value.

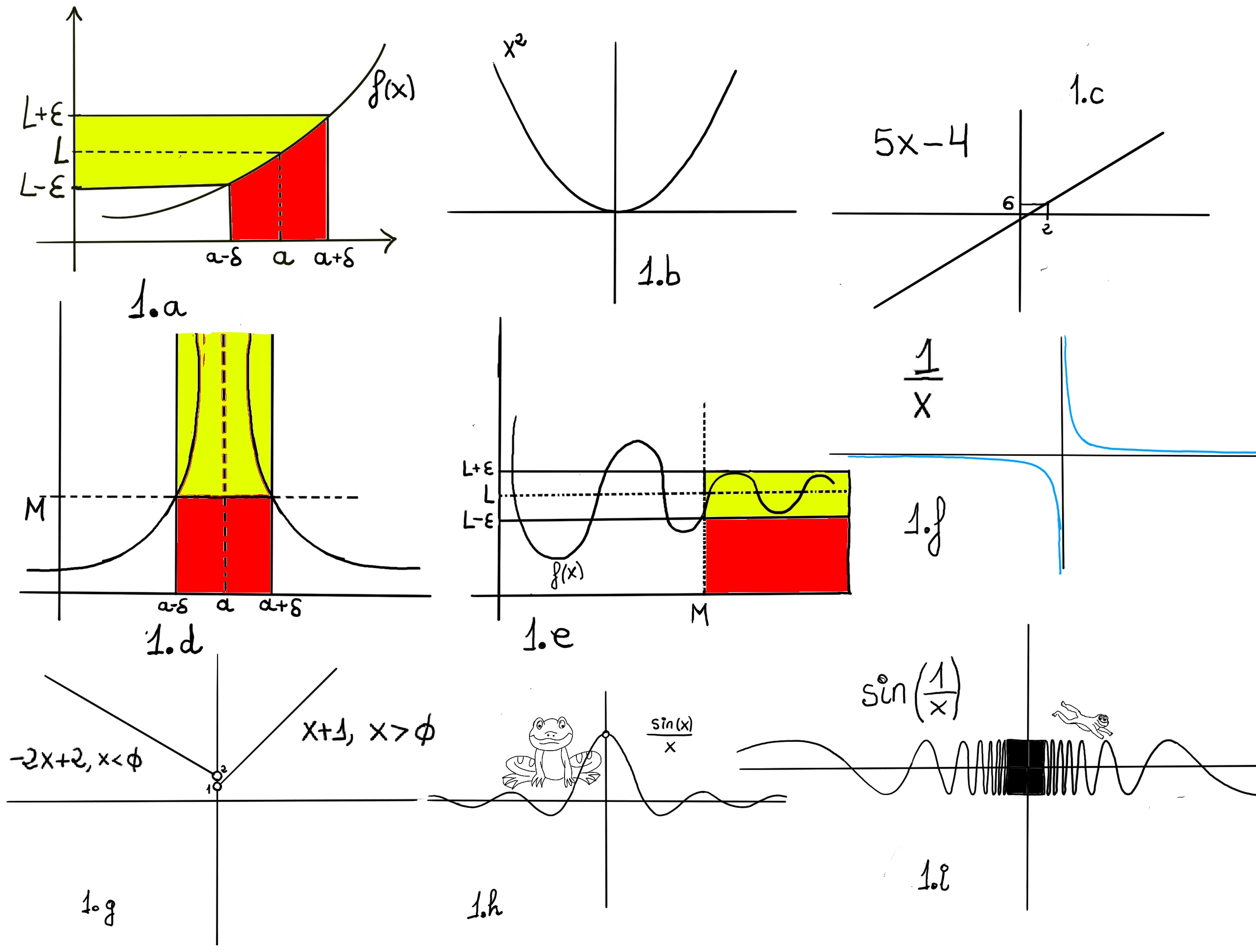
One would say that the limit of f, as x approaches a, is L, $\lim_{x \to a} f(x)=L$. Formally, for every real ε > 0, there exists a real δ > 0 such that for all real x, 0 < | x − a | < δ implies that | f(x) − L | < ε. In other words, f(x) gets closer and closer to L, f(x)∈ (L-ε, L+ε), as x moves closer and closer -approaching closer but never touching- to a (x ∈ (a-δ, a+δ), x≠a) -Fig 1.a.-

Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = L$ if

$\forall \epsilon>0, \exists \delta>0: 0<|x-a|<\delta, implies~ |f(x)-L|<\epsilon$

Or

$\forall \epsilon>0, \exists \delta>0: |f(x)-L|<\epsilon, whenever~ 0<|x-a|<\delta$   

Strategy in finding limits

Don’t worry, you are not alone. Calculating limits can be confusing and challenging for many students. But don’t worry, you are in the right place. Here are some common strategies and techniques for evaluating limits:

• Direct substitution. The first step is to directly evaluate the function at the value that the independent variable approaches. If the function is defined at that point, we can obtain the limit value directly.

1. $\lim_{x \to 0} x^2 = 0$.
2. $\lim_{x \to 2} 5x -4 = 5·2 -4 = 6$.

• Finding a limit by factoring is a technique to computing limits that works by canceling out common factors. It allows us to transform an indeterminate form into one that allows for direct evaluation. Notice that the limit as x approaches 2 has nothing no to do with the value of the function at x = 2.

1. $\lim_{x \to 2}\frac{x^2-4}{x-2} =\lim_{x \to 2}\frac{(x+2)(x-2)}{x-2} = \lim_{x \to 2}(x+2)=4$.
2. $\lim_{x \to 4} \frac{\sqrt{x}-2}{x-4} = \lim_{x \to 4} \frac{(\sqrt{x}-2)(\sqrt{x}+2)}{(x-4)(\sqrt{x}+2)} = \lim_{x \to 4} \frac{x-4}{(x-4)(\sqrt{x}+2)} = \lim_{x \to 4} \frac{1}{\sqrt{x}+2} = \frac{1}{4}.$

• When the expression inside the limit contains a sum or difference of fractions, it sometimes works to combine the fractions.

1. $\lim_{x \to 2} \frac{\frac{1}{x}-\frac{1}{2}}{x-2} = \lim_{x \to 2} \frac{\frac{2-x}{2x}}{x-2} = \lim_{x \to 2} \frac{-1}{2x} = \frac{-1}{4}$
2. $\lim_{x \to 2}(\frac{1}{4x-8}-\frac{1}{x^2-4}) = \lim_{x \to 2} (\frac{1}{4(x-2)}-\frac{1}{(x-2)(x+2)}) = \lim_{x \to 2} (\frac{(x+2) - 4}{4(x-2)(x+2)}) = \lim_{x \to 2} \frac{x-2}{4(x-2)(x+2)} = \lim_{x \to 2} \frac{1}{4(x+2)} = \frac{1}{16}.$
3. $\c$=[∞-∞] $\lim_{x \to 2} \frac{4-(x+2)}{(x-2)(x+2)} = \lim_{x \to 2} \frac{(2-x)}{(x-2)(x+2)} = \lim_{x \to 2} \frac{-1}{(x+2)} = \frac{-1}{4}.$

• The conjugate method (Rationalization). When the expression inside the limit contains a radical expression, it sometimes works to rationalize, that is, multiply numerator and denominator by a radical that will get rid of the radical in the denominator (or numerator).

1. $\lim_{x \to 0} \frac{\sqrt{1+x}-1}{x} = \lim_{x \to 0} \frac{\sqrt{1+x}-1}{x}·\frac{\sqrt{1+x}+1}{\sqrt{1+x}+1} = \lim_{x \to 0} \frac{(1+x)-1}{x(\sqrt{1+x}+1)} = \lim_{x \to 0} \frac{x}{x(\sqrt{1+x}+1)} = \lim_{x \to 0} \frac{1}{(\sqrt{1+x}+1)} = \frac{1}{2}$.
2. $\lim_{x \to 0} (\frac{3}{x\sqrt{9-x}}-\frac{1}{x})$[Combine the fractions] $\lim_{x \to 0} (\frac{3-\sqrt{9-x}}{x\sqrt{9-x}}) = \lim_{x \to 0} (\frac{3-\sqrt{9-x}}{x\sqrt{9-x}}·\frac{3+\sqrt{9-x}}{3+\sqrt{9-x}}) = \lim_{x \to 0} \frac{9-(9-x)}{(x\sqrt{9-x})(3+\sqrt{9-x})} = \lim_{x \to 0} \frac{x}{(x\sqrt{9-x})(3+\sqrt{9-x})} = \lim_{x \to 0} \frac{1}{(\sqrt{9-x})(3+\sqrt{9-x})} = \frac{1}{\sqrt{9}(3+\sqrt{9})} = \frac{1}{3·6} = \frac{1}{18}$
3. $\lim_{x \to 2} \frac{3-\sqrt{2x+5}}{x-2} = \lim_{x \to 2} \frac{3-\sqrt{2x+5}}{x-2}\frac{3+\sqrt{2x+5}}{3+\sqrt{2x+5}} = \lim_{x \to 2} \frac{9-(2x+5)}{(x-2)(3+\sqrt{2x+5})} = \lim_{x \to 2} \frac{-2x+4}{(x-2)(3+\sqrt{2x+5})} = \lim_{x \to 2} \frac{-2(x-2)}{(x-2)(3+\sqrt{2x+5})} = \lim_{x \to 2} \frac{-2}{(3+\sqrt{2x+5})} = \frac{-2}{3+\sqrt{9}} = \frac{-2}{6} = \frac{-1}{3}$
4. $\lim_{x \to 9} \frac{x-9}{\sqrt{x}-3} = \lim_{x \to 9} \frac{(x-9)(\sqrt{x}+3)}{(\sqrt{x}-3)(\sqrt{x}+3)} = \lim_{x \to 9} \frac{(x-9)(\sqrt{x}+3)}{x-9} = \lim_{x \to 9} \sqrt{x}+3 = \sqrt{9} + 3 = 6.$
5. $\lim_{x \to 0} \frac{1}{x\sqrt{x+1}}-\frac{1}{x} =$ [∞-∞] $\lim_{x \to 0} \frac{1-\sqrt{x+1}}{x\sqrt{x+1}} = \lim_{x \to 0} \frac{1-\sqrt{x+1}}{x\sqrt{x+1}} \frac{1+\sqrt{x+1}}{1+\sqrt{x+1}} = \lim_{x \to 0} \frac{1-(x+1)}{x\sqrt{x+1}(1+\sqrt{x+1})} = \lim_{x \to 0} \frac{-x}{x\sqrt{x+1}(1+\sqrt{x+1})} = \lim_{x \to 0} \frac{-1}{\sqrt{x+1}(1+\sqrt{x+1})} = \frac{-1}{2}$

• The Squeeze Theorem. Let f, g, and h be functions defined on an interval I that contains x = a, except possibly at x = a. Suppose that for every x in I not equal to a, we have g(x) ≤ f(x) ≤ h(x), and also suppose that $\lim_{x \to a} g(x) = \lim_{x \to a} h(x) = L.$ Then, $\lim_{x \to a} f(x) = L.$

1. $\lim_{x \to 0} f(x), ~where~f(x)= x·sin(\frac{1}{x}) = 0$ for x ≠ 0, and f(0) = 0 (Figure i). 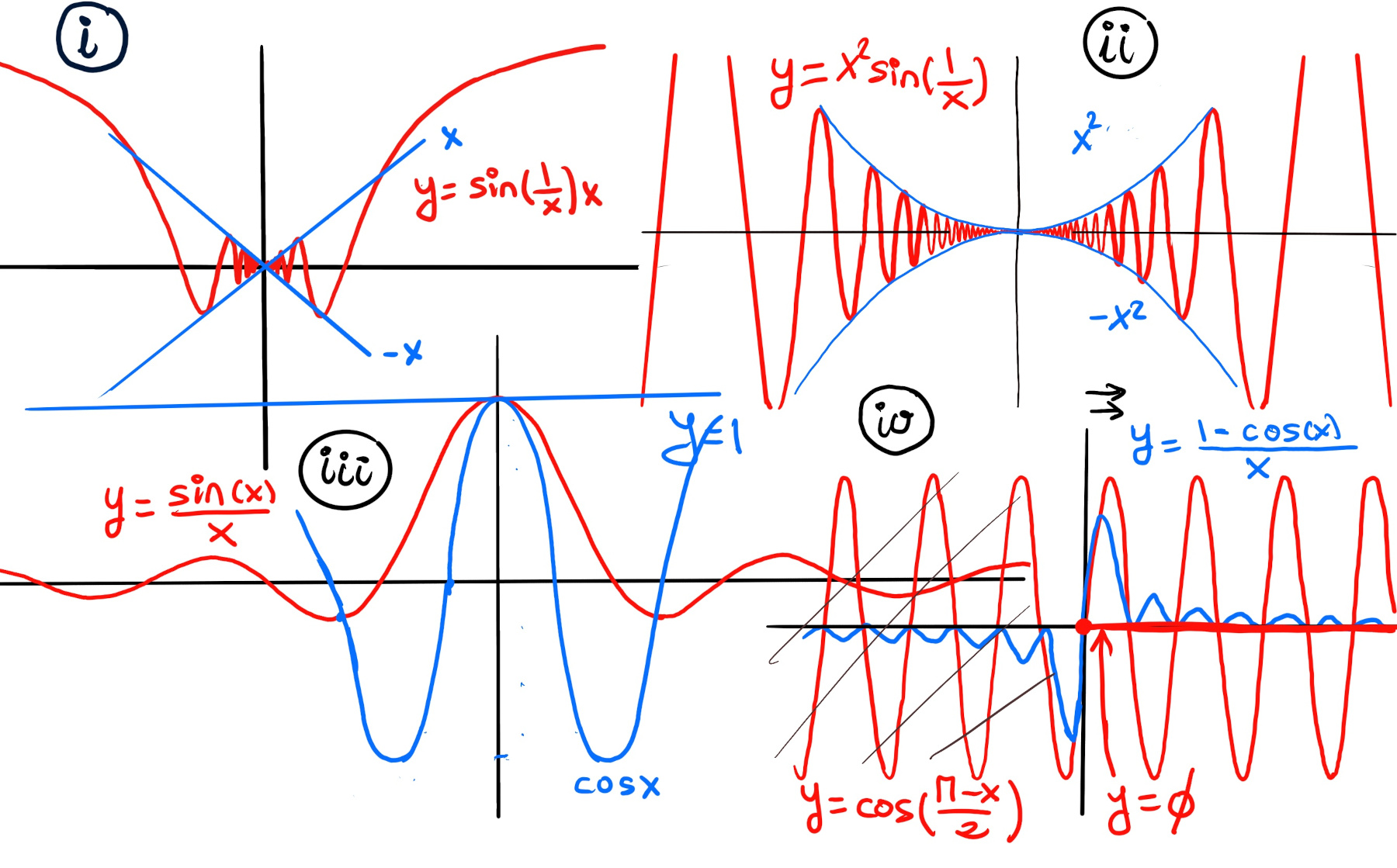$-1 ≤ sin(\frac{1}{x}) ≤ 1 ⇨ -x ≤ xsin(\frac{1}{x}) ≤ x$

   $\lim_{x \to 0} x = \lim_{x \to 0} -x = 0.$ Then, by the Squeeze Theorem, $\lim_{x \to 0} x·sin(\frac{1}{x}) = 0$.

2. $\lim_{x \to 0} (\frac{sin(x)}{x}) = 1,$ (Figure iii)

    

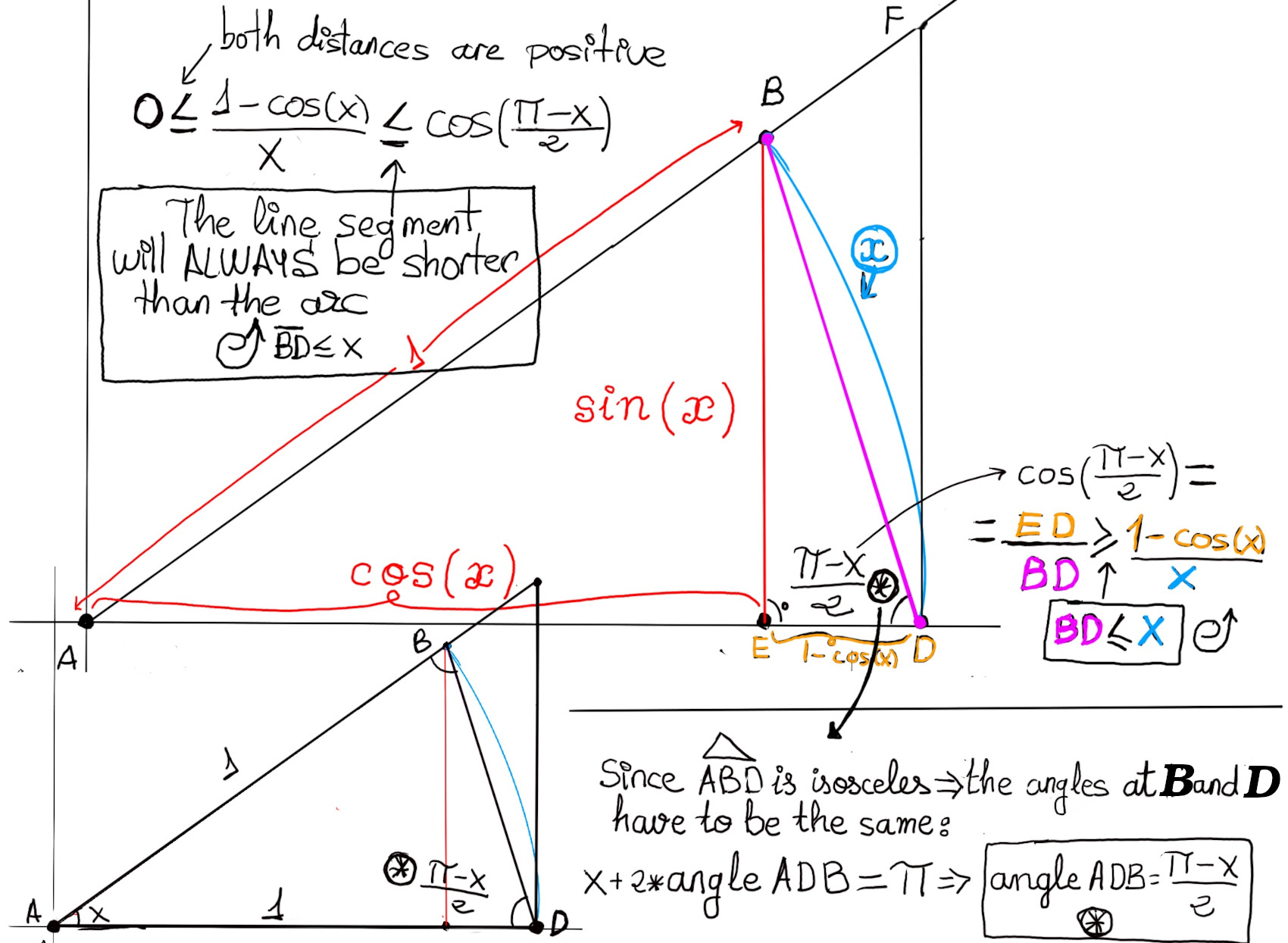
   $Area(\triangle ADF) ≥ Area(Sector ADB) ≥ Area(\triangle ADB)$ ⇨ $\frac{tan(x)}{2} ≥ \frac{x}{2} ≥ \frac{sin(x)}{2}$ because the Area of a circle with an angle measuring 360º is πr² ⇨ Area of a sector (θ is measured in degrees) is ^θ⁄_360ºπr² ⇨ Area(Sector ADB) = ¹⁄₂r²θ, where θ is the angle in radians =[r = 1] ¹⁄₂θ, and then consider that x = θ.

   $ ⇨ \frac{sin(x)}{cos(x)} ≥ x ≥ sin(x) ⇨ \frac{cos(x)}{sin(x)} ≤ \frac{1}{x} ≤\frac{1}{sin(x)} ⇨ cos(x) ≤ \frac{sin(x)}{x} ≤1$

   $\lim_{x \to 0} cos(x) = \lim_{x \to 0} 1 = 1$ ⇨[by the Squeeze Theorem] $\lim_{x \to 0} (\frac{sin(x)}{x}) = 1.$

3. $\lim_{x \to 0} (\frac{1-cos(x)}{x}) = 0,$ (Figure iv). 

     $\lim_{x \to 0} cos(\frac{\pi-x}{2}) = \lim_{x \to 0} 0 = 0, \lim_{x \to 0} 0 = 0$ ⇨[By the squeeze theorem] $\lim_{x \to 0} (\frac{1-cos(x)}{x}) = 0.$

4. $\lim_{x \to 0} x^2·e^{sin(\frac{1}{x})}$

   $-1 ≤ sin(\frac{1}{x}) ≤ 1 ⇒$[The exponential is a monotone increasing function] $e^{-1} ≤ e^{sin(\frac{1}{x})} ≤ e^1 ⇒ x^2e^{-1} ≤ x^2e^{sin(\frac{1}{x})} ≤ x^2e$

   $\lim_{x \to 0} x^2e = e·\lim_{x \to 0} x^2 = e·0 = 0, \lim_{x \to 0} x^2e^{-1} = e^{-1}·\lim_{x \to 0} x^2 = e^{-1}·0 = 0$ ⇒[By the Squeeze Theorem] $\lim_{x \to 0} x^2·e^{sin(\frac{1}{x})} = 0.$

• If $\lim_{x \to a} = \frac{n}{0}$, the limit does not exist. If both one-sided limits are the same, we say $\lim_{x \to a} f(x) = ∞,~or~ \lim_{x \to a} f(x) = -∞$ meaning that the limit does not exist, but we know the function is growing infinitely large or small.

1. $\lim_{x \to 0} \frac{1}{x^2} = ∞$ because $\lim_{x \to 0⁺} \frac{1}{x^2} = \lim_{x \to 0⁻} \frac{1}{x^2} = ∞$.
2. $\lim_{x \to 2} \frac{x^2+4}{x^3-8}$ does not exist because $\lim_{x \to 2⁺} \frac{x^2+4}{x^3-8} = \frac{8}{0⁺} = ∞, \lim_{x \to 2⁻} \frac{x^2+4}{x^3-8} = \frac{8}{0⁻} = -∞$.
3. $\lim_{x \to 3} \frac{x-4}{x^2-6x+9} = \lim_{x \to 3} \frac{x-4}{(x-3)^2} = -∞$ because $\lim_{x \to 3⁺} \frac{x-4}{x^2-6x+9} = \lim_{x \to 3⁺} \frac{x-4}{(x-3)^2} = -∞ = \lim_{x \to 3⁻} \frac{x-4}{x^2-6x+9} = \lim_{x \to 3⁻} \frac{x-4}{(x-3)^2} = -∞$.

• Limits Involving Trigonometric Functions. We can change the expression inside the limit using trigonometric identities or L'Hôpital's rule.

1. $\lim_{θ \to 0} \frac{sin(θ)}{sin(2θ)}$ =[We can use the trigonometric identity sin(2θ) = 2sin(θ)cos(θ)] $\lim_{θ \to 0} \frac{sin(θ)}{2sin(θ)cos(θ)} = \lim_{θ \to 0} \frac{1}{2·cos(θ)} = \frac{1}{2·1} = \frac{1}{2}.$
2. $\lim_{x \to \frac{π}{4}} \frac{sin(x)-cos(x)}{cos^2(x)-sin^2(x)}$ =[The denominator is a difference of perfect squares, let’s factor it] $\lim_{x \to \frac{π}{4}} \frac{sin(x)-cos(x)}{(cos(x)-sin(x))(cos(x)+sin(x))} = \lim_{x \to \frac{π}{4}} \frac{-1}{(cos(x)+sin(x))} = \frac{-1}{\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}} = \frac{-1}{\sqrt{2}} = \frac{-1}{\sqrt{2}}\frac{\sqrt{2}}{\sqrt{2}} = \frac{-\sqrt{2}}{2}$
3. $\lim_{x \to \frac{π}{2}} \frac{cos(2x)}{tan(x)}$ =[cos(2θ) = cos²(θ)-sin²(θ) = 1 -2sin²(θ)] $\lim_{x \to \frac{π}{2}} \frac{1-2sin^2(x)}{\frac{sin(x)}{cos(x)}} = \lim_{x \to \frac{π}{2}} \frac{1-2sin^2(x)}{1}·\frac{cos(x)}{sin(x)} = \lim_{x \to \frac{π}{2}} \frac{(1-2sin^2(x))cos(x)}{sin(x)}=\frac{(1-2)·0}{1} = 0.$
4. $\lim_{x \to 0} \frac{1-cos(x)}{x^2}$ = [$1-cos(x)=2sin^2(\frac{x}{2})$] = $\lim_{x \to 0} \frac{2sin^2(\frac{x}{2})}{x^2} =$[Multiplication law, states that the limit of a product of two functions equals the product of the limits of both functions, $\lim_{x \to a} (f(x)·g(x)) = lim_{x \to a} f(x) · lim_{x \to a} g(x).$ ] $2·\lim_{x \to 0} \frac{sin(\frac{x}{2})}{x}\lim_{x \to 0} \frac{sin(\frac{x}{2})}{x} = \frac{2}{4}·\lim_{x \to 0} \frac{sin(\frac{x}{2})}{\frac{x}{2}}\lim_{x \to 0} \frac{sin(\frac{x}{2})}{\frac{x}{2}} = \frac{2}{4}·1·1 = \frac{1}{2}$ Notice: Substitution is a general method used to simplify complicated expressions by assigning a simple name to some part of that expression, in our case $\frac{x}{2} = u$, and notice that x→0 ↭ u→0, and $\lim_{u \to 0} \frac{sin(u)}{u} = 1$ -The squeezing theorem, example 2-.
5. $\lim_{x \to 0} \frac{1-cos(x)}{x^2} = \lim_{x \to 0} \frac{1-cos(x)}{x^2} \frac{1+cos(x)}{1+cos(x)} = \lim_{x \to 0} \frac{1-cos^2(x)}{x^2(1+cos(x))} =$ [cos²(x)+sin²(x) = 1 ⇒ 1 -cos²(x) = sin²(x)] $\lim_{x \to 0} \frac{sin^2(x)}{x^2(1+cos(x))}$ = [Multiplication law, states that the limit of a product of two functions equals the product of the limits of both functions, $\lim_{x \to a} (f(x)·g(x)) = lim_{x \to a} f(x) · lim_{x \to a} g(x).$ ] $\lim_{x \to 0} \frac{sin(x)}{x}·\lim_{x \to 0} \frac{sin(x)}{x}·\lim_{x \to 0} \frac{1}{1+cos(x)} = 1·1·\frac{1}{1+1} = \frac{1}{2}.$ Notice that $\lim_{u \to 0} \frac{sin(u)}{u} = 1$ -The squeezing theorem, example 2-.
6. $\lim_{x \to 0} \frac{cos(2x)-1}{cos(x)-1}$ =[cos(a + b) = cos(a)·cos(b) - sin(a)·sin(b) ⇒ cos(2x) = cos(x + x) = cos(x)·cos(x) - sin(x)·sin(x) = cos²(x) -sin²(x) = cos²(x) -(1 -cos²(x)) = 2cos²(x) -1] $\lim_{x \to 0} \frac{(2cos^2(x)-1)-1}{cos(x)-1} = \lim_{x \to 0} \frac{2cos^2(x)-2}{cos(x)-1} = 2·\lim_{x \to 0} \frac{cos^2(x)-1}{cos(x)-1} = 2·\lim_{x \to 0} \frac{(cos(x)-1)(cos(x)+1)}{cos(x)-1} = 2·\lim_{x \to 0} cos(x) + 1 = 2·(1+1) = 4.$

• L’Hôpital’s Rule is a mathematical technique used to evaluate limits of indeterminate forms using derivatives. It states that for functions f and g which are differentiable on an interval I except possible at a point “a” contained in I, if $\lim_{x \to a} f(x) = \lim_{x \to a} g(x) = 0$ or ± ∞, and g'(x) ≠ 0 ∀x ∈ I, except possible at a, then $\lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a} \frac{f'(x)}{g'(x)},$ provided that the right hand limit exists or equals ± ∞.

1. $\lim_{x \to 0}\frac{cos(x)-1}{x^2}$ =[L’Hôpital’s Rule] $\lim_{x \to 0}\frac{-sin(x)}{2x}$ = [There may be instances where we would need to apply L’Hôpital’s Rule multiple times] $\lim_{x \to 0}\frac{-cos(x)}{2} = \frac{-1}{2}.$
2. $\lim_{x \to 0^+} xln(x)$ =[It seems that L’Hôpital’s Rule does not apply, 0·(-∞)] $\lim_{x \to 0^+} \frac{ln(x)}{1/x}$ = [L’Hôpital’s Rule] $\lim_{x \to 0^+} \frac{1/x}{-1/x^2} = \lim_{x \to 0^+} -x = 0$
3. $\lim_{x \to ∞} \frac{ln(x)}{x^{1/3}}$ =[L’Hôpital’s Rule, ∞/∞] $\lim_{x \to ∞} \frac{1/x}{1/3·x^{-2/3}} =\lim_{x \to ∞} 3x^{2/3-1} =\lim_{x \to ∞} 3x^{-1/3} = 0.$ In words, ln(x) grows slower than $x^{1/3}$ or any arbitrary positive power of x.
4. $\lim_{x \to 0+} x^x$ =[Recall that a^b=e^bln(a)] $\lim_{x \to 0+} e^{xln(x)}$. Notice that $\lim_{x \to 0+} xln(x) = \lim_{x \to 0+} \frac{ln(x)}{1/x} = \lim_{x \to 0+} \frac{1/x}{-1/x^2} = \lim_{x \to 0+} -x = 0 ⇒ \lim_{x \to 0+} x^x = \lim_{x \to 0+} e^{xln(x)} = e^0 = 1.$
5. $\lim_{x \to 0} \frac{sin(x)}{x}$ =[L’Hôpital’s Rule, 0/0] $\lim_{x \to 0} \frac{cos(x)}{1} = cos(0) = 1.$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus.
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
9. blackpenredpen.