The Squeeze Theorem

Most important numbers are not 0, 1, the golden ratio, π, e, i, Graham’s number, Planck’s or Avogadro’s constant, but your ATP Pin number, your girlfriend phone number, then your mother-in-law phone number, and finally your divorce solicitor’s number, Anawim, justtothepoint.com.

Recall

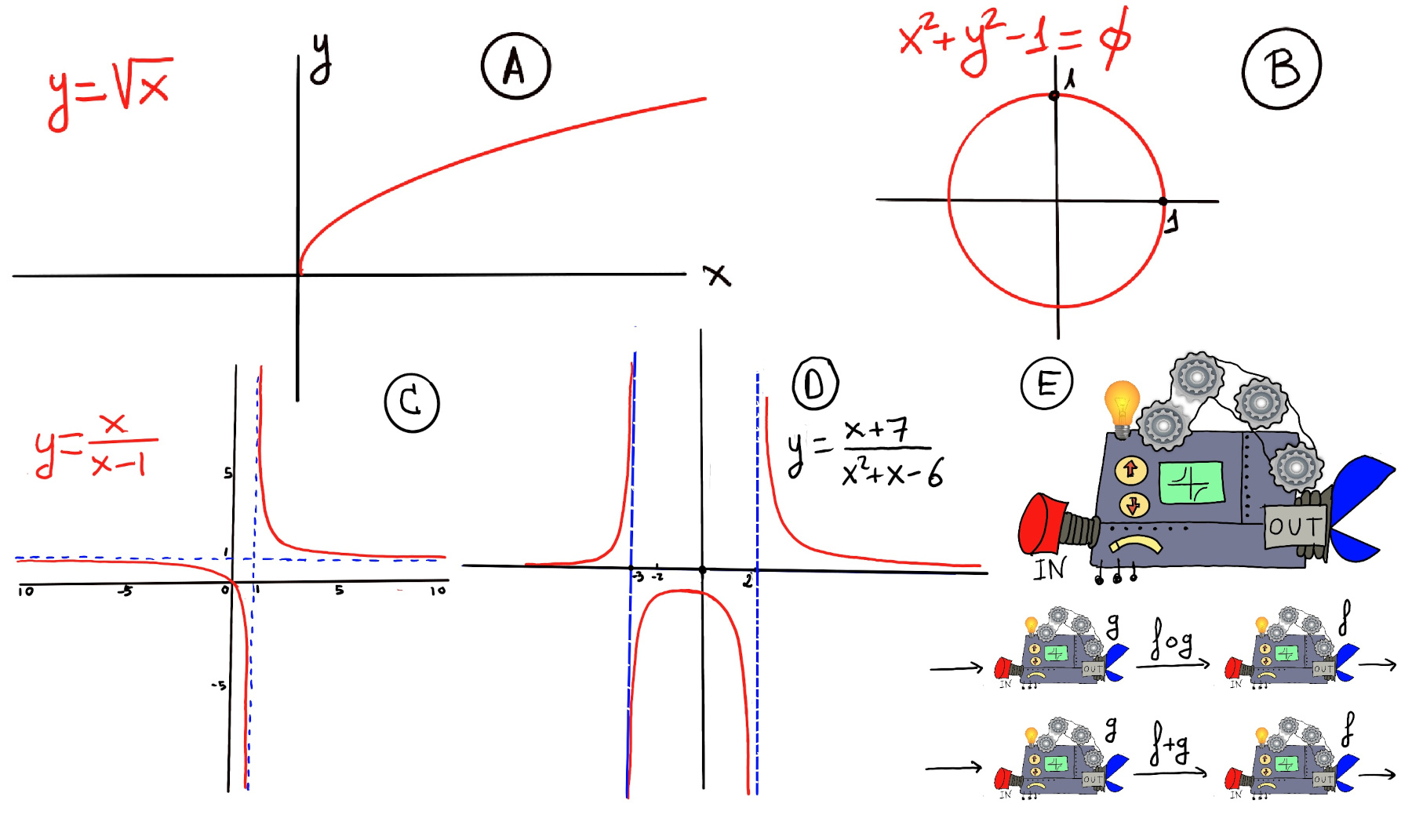
Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).

The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ. A mathematical function is like a black box that takes certain input values and generates corresponding output values (Figure E).

Very loosing speaking, a limit is the value to which a function grows close as the input get closer and closer to some other given value.

One would say that the limit of f, as x approaches a, is L, $\lim_{x \to a} f(x)=L$. Formally, for every real ε > 0, there exists a real δ > 0 such that for all real x, 0 < | x − a | < δ implies that | f(x) − L | < ε. In other words, f(x) gets closer and closer to L, f(x)∈ (L-ε, L+ε), as x moves closer and closer -approaching closer but never touching- to a (x ∈ (a-δ, a+δ), x≠a)) -Fig 1.a.-

Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = L$ if

$\forall \epsilon>0, \exists \delta>0: 0<|x-a|<\delta, implies~ |f(x)-L|<\epsilon$

Or

$\forall \epsilon>0, \exists \delta>0: |f(x)-L|<\epsilon, whenever~ 0<|x-a|<\delta$   

The Squeeze Theorem

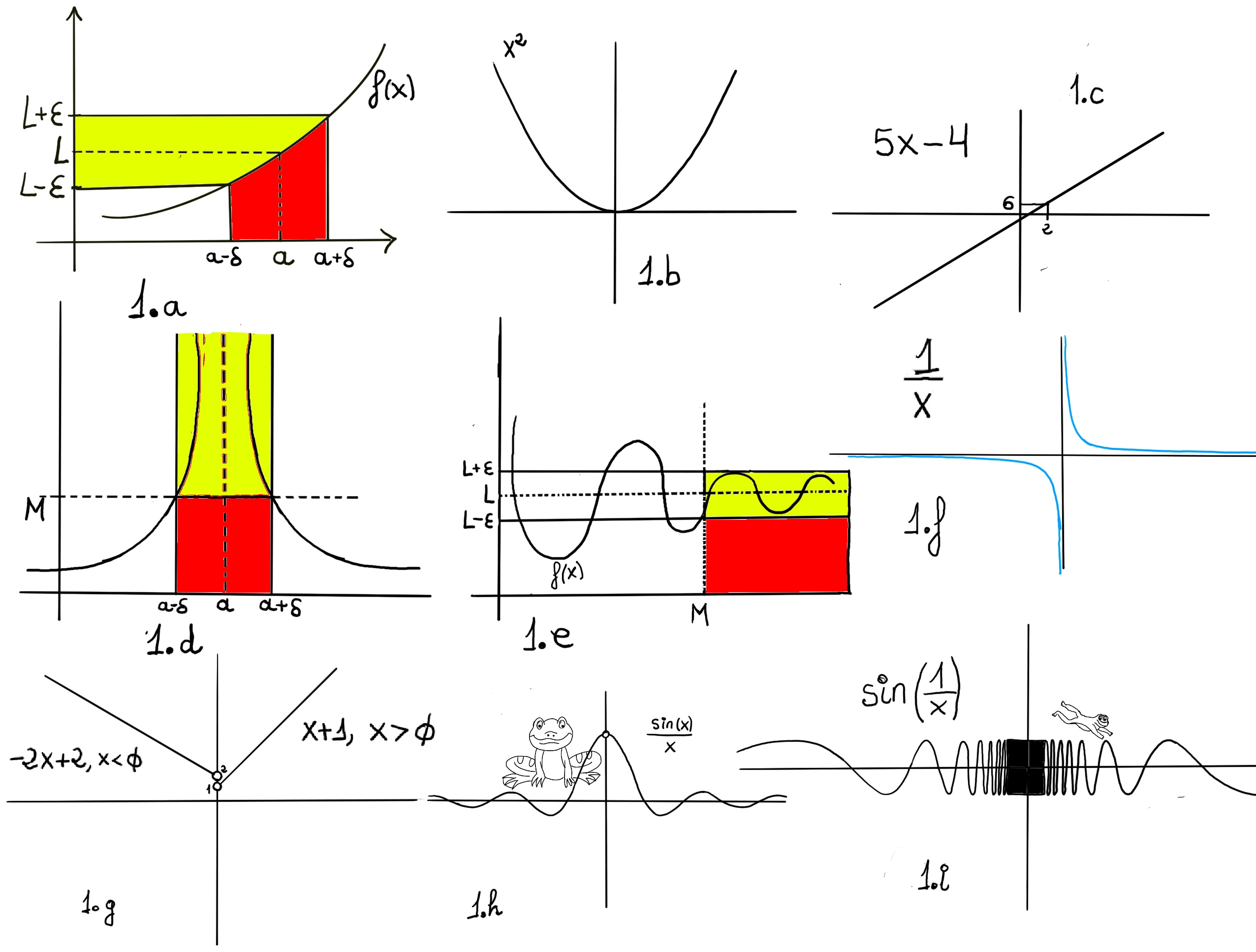
The squeeze or sandwich theorem. If a function f lies between two functions g and h, and the limits of each of them at a particular point are equal to L, then the limit of f at that particular point is also equal to L.

The theorem is particularly useful when direct substitution or algebraic manipulation is challenging.

Intuitive Explanation: The Squeeze Theorem helps determine the limit of a function by comparing it to two other functions whose limits are known. If f(x) is “sandwiched” between g(x) and h(x), and both g(x) and h(x) approach the same limit L as x approaches a certain value, say a, then f(x) must also approach that limit at that point.

Formal definition. Let f, g, and h be functions defined on an interval I that contains x = a, except possibly at x = a. Suppose that for every x in I not equal to a, we have g(x) ≤ f(x) ≤ h(x), and also suppose that $\lim_{x \to a} g(x) = \lim_{x \to a} h(x) = L.$ Then, $\lim_{x \to a} f(x) = L.$

Proof: $\forall \epsilon>0, \exists \delta_1>0: 0<|x-a|<\delta_1,~implies~ |g(x)-L|<\epsilon~ *_1$

$\forall \epsilon>0, \exists \delta_2>0: 0<|x-a|<\delta_2,~implies~ |h(x)-L|<\epsilon~ *_2$

Let’s choose as $\delta = min(\delta_1, \delta_2)$ $\forall \epsilon>0, \exists \delta>0: 0<|x-a|<\delta,~implies~$

$L -\epsilon < g(x) < L +\epsilon$ [*₁] and $L -\epsilon < h(x) < L +\epsilon$ [*₂]

$L -\epsilon < g(x) ≤ f(x) ≤ h(x) < L +\epsilon ⇨ L -\epsilon < f(x) < L +\epsilon ⇨ |f(x)-L|<\epsilon$ ∎

Exercises

• $\lim_{x \to 0} f(x), ~where~f(x)= x·sin(\frac{1}{x}) = 0$ for x ≠ 0, and f(0) = 0 (Figure i).  

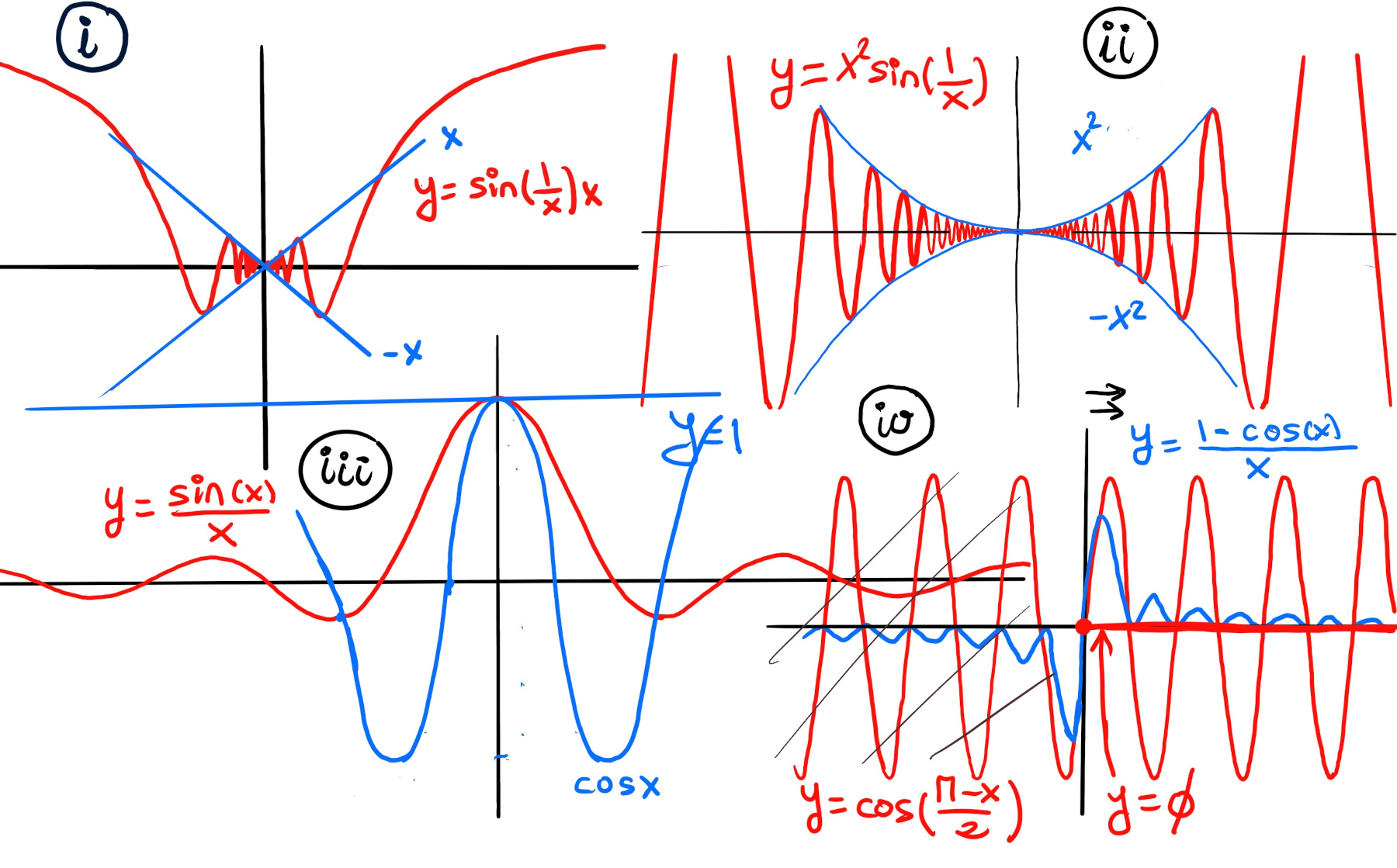
$-1 ≤ sin(\frac{1}{x}) ≤ 1 ⇨ -x ≤ xsin(\frac{1}{x}) ≤ x$

$\lim_{x \to 0} x = \lim_{x \to 0} -x = 0.$ Then, by the Squeeze Theorem, $\lim_{x \to 0} x·sin(\frac{1}{x}) = 0$.

• $\lim_{x \to 0} x^{2} sin(\frac{1}{x}) = 0$ (Figure ii).

$-1 ≤ sin(\frac{1}{x}) ≤ 1 ⇨ -x^{2} ≤ x^{2}sin(\frac{1}{x}) ≤ x^{2}$

$\lim_{x \to 0} x^{2} = \lim_{x \to 0} -x^{2} = 0.$ Then, by the Squeeze Theorem, $\lim_{x \to 0} x^{2} sin(\frac{1}{x}) = 0$.

• $\lim_{x \to ∞} \frac{cos^2(2x)}{3-2x}$

From basic trigonometry, -1 ≤ cos(2x) ≤ 1 ⇒[x² ≥ 0] 0 ≤ cos²(2x) ≤ 1 ⇒[Since we are calculating the limit as x goes to infinity, it is completely reasonable to assume that 3 - 2x < 0] $\frac{0}{3-2x}≥\frac{cos^2(2x)}{3-2x}≥\frac{1}{3-2x}⇒ \frac{1}{3-2x}≤\frac{cos^2(2x)}{3-2x}≤0$

$\lim_{x \to ∞} 0 = 0, \lim_{x \to ∞} \frac{1}{3-2x} = 0 ⇒ \lim_{x \to ∞} \frac{cos^2(2x)}{3-2x} = 0.$

• $\lim_{x \to ∞} \frac{x^2(sin(x)+cos^3(x))}{(x^2+1)(x-3)}$

From basic trigonometry, -1 ≤ cos(x) ≤ 1, -1 ≤ sin(x) ≤ 1 ⇒ -1 ≤ cos³(x) ≤ 1 ⇒ -2 ≤ sin(x) + cos³(x) ≤ 2 ⇒ [Since we are calculating the limit as x goes to minus infinity, it is completely reasonable to assume that x-3 < 0] $\frac{2}{x-3}≤\frac{sin(x)+cos^3(x)}{x-3}≤\frac{-2}{x-3}$

Next, we are going to multiply by x² and divide by x² +1 (both positive),

$\frac{2x^2}{(x^2+1)(x-3)}≤\frac{x^2(sin(x)+cos^3(x))}{(x^2+1)(x-3)}≤\frac{-2x^2}{(x^2+1)(x-3)}$

$\lim_{x \to ∞} \frac{2x^2}{(x^2+1)(x-3)} = \lim_{x \to ∞}\frac{2x^2}{x^3-3x^2+x-3}$ =[Apply L’Hôpital’s rule or divide by x³ 🏮] = $\lim_{x \to ∞}\frac{\frac{2}{x}}{1-3\frac{1}{x}+\frac{1}{x^2}-3\frac{1}{x^3}} = 0$. Mutatis mutandis, $\lim_{x \to ∞} \frac{-2x^2}{(x^2+1)(x-3)}$ = 0, and so by the squeezing theorem, $\lim_{x \to ∞} \frac{x^2(sin(x)+cos^3(x))}{(x^2+1)(x-3)} = 0.$

🏮 To evaluate the limits at infinity for a rational function, we divide the numerator and denominator by the highest power of x appearing in the denominator. This determines which term in the overall expression dominates the behavior of the function at large values of x.

• $\lim_{x \to 0} (\frac{sin(x)}{x}) = 1,$ (Figure iii)  

Let’s prove it geometrically. The arc length of a circle in radians can be expressed as, Arc Length = $\theta·r = x~ because~ r=1.$ Notice that as x→0, the bow string is the same size than the bow itself, that is, $\lim_{x \to 0} (\frac{sin(x)}{x}) = 1.$ -1.b.-  

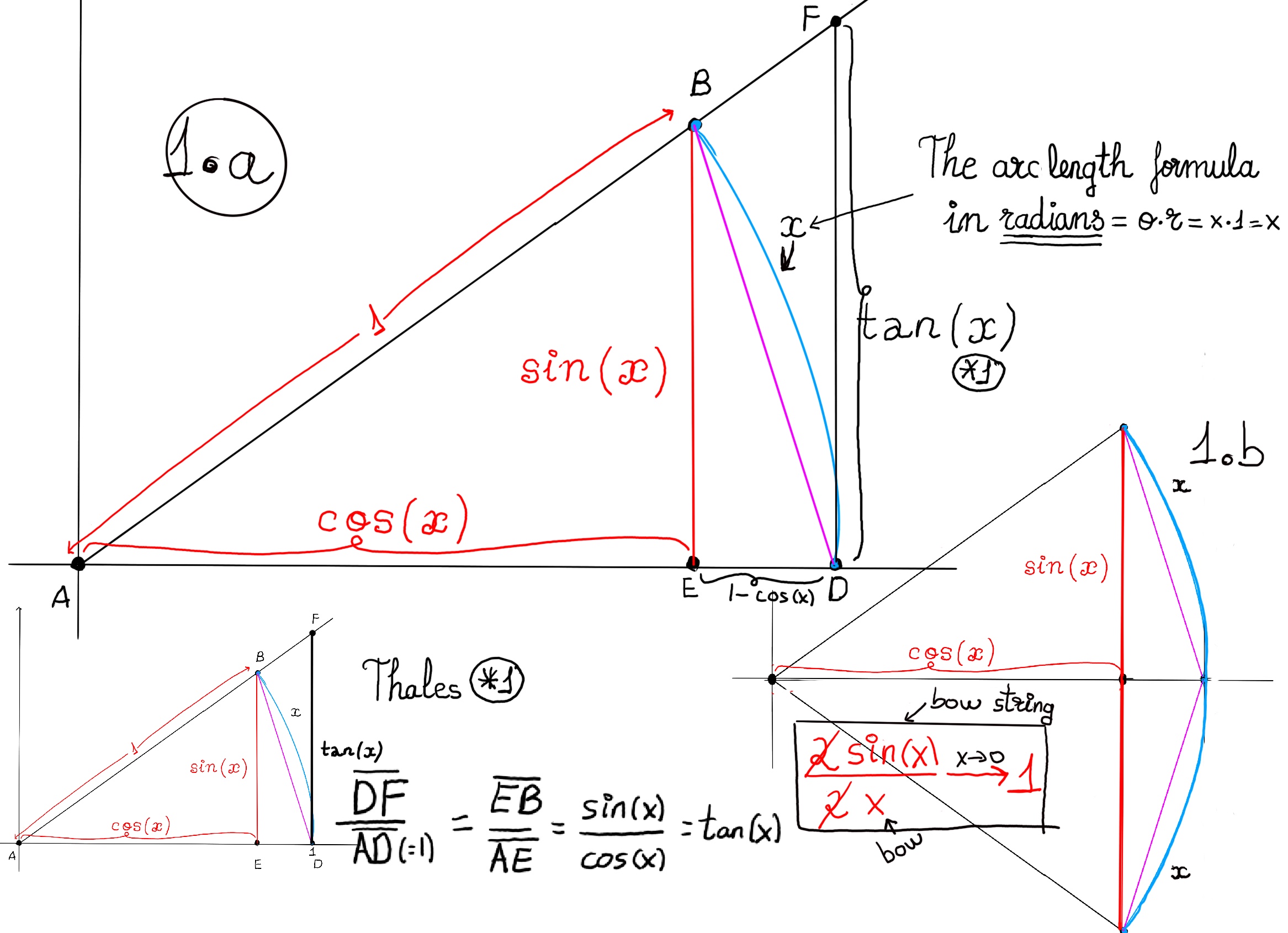
Another way of proving it is as follows: -1.a.-

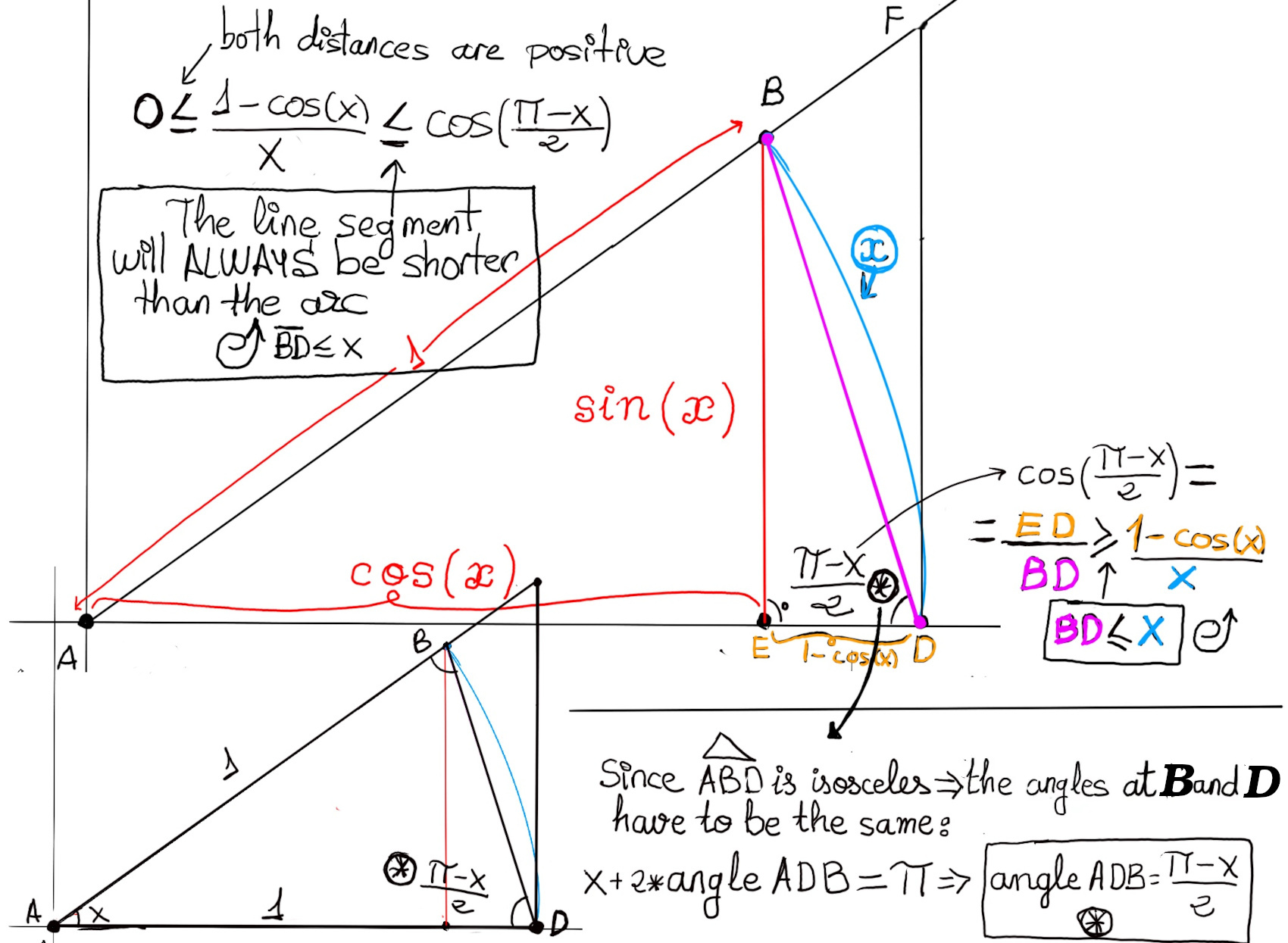
$Area(\triangle ADF) ≥ Area(Sector ADB) ≥ Area(\triangle ADB)$ $ ⇨ \frac{tan(x)}{2} ≥ \frac{x}{2} ≥ \frac{sin(x)}{2}$ because the Area of a circle with an angle measuring 360º is πr² ⇨ Area of a sector (θ is measured in degrees) is ^θ⁄_360ºπr² ⇨ Area(Sector ADB) = ¹⁄₂r²θ, where θ is the angle in radians =[r = 1] ¹⁄₂θ, and then consider that x = θ.

$ ⇨ \frac{sin(x)}{cos(x)} ≥ x ≥ sin(x) ⇨ \frac{cos(x)}{sin(x)} ≤ \frac{1}{x} ≤\frac{1}{sin(x)} ⇨ cos(x) ≤ \frac{sin(x)}{x} ≤1$

$\lim_{x \to 0} cos(x) = \lim_{x \to 0} 1 = 1$ ⇨[by the Squeeze Theorem] $\lim_{x \to 0} (\frac{sin(x)}{x}) = 1.$

• $\lim_{x \to 0} (\frac{1-cos(x)}{x}) = 0,$ (Figure iv).

  $\lim_{x \to 0} cos(\frac{\pi-x}{2}) = \lim_{x \to 0} 0 = 0, \lim_{x \to 0} 0 = 0$ ⇨[By the squeeze theorem] $\lim_{x \to 0} (\frac{1-cos(x)}{x}) = 0.$

It can also be solved as follows,

$\lim_{x \to 0} (\frac{1-cos(x)}{x}) = \lim_{x \to 0} (\frac{(1-cos(x))(1+cos(x))}{x(1+cos(x))}) = \lim_{x \to 0} (\frac{1-cos^{2}(x)}{x(1+cos(x))}) = \lim_{x \to 0} (\frac{sin^{2}(x)}{x(1+cos(x))})$

$ = \lim_{x \to 0} (\frac{sin(x)}{x}\frac{sin(x)}{1+cos(x)}) = \lim_{x \to 0} (\frac{sin(x)}{x}) \lim_{x \to 0}(\frac{sin(x)}{1+cos(x)})$ [by the product law for limits] = 1·0 = 0.

• $\lim_{x \to 0} x^2·e^{sin(\frac{1}{x})}$

$-1 ≤ sin(\frac{1}{x}) ≤ 1 ⇒$[The exponential is a monotone increasing function] $e^{-1} ≤ e^{sin(\frac{1}{x})} ≤ e^1 ⇒ x^2e^{-1} ≤ x^2e^{sin(\frac{1}{x})} ≤ x^2e$

$\lim_{x \to 0} x^2e = e·\lim_{x \to 0} x^2 = e·0 = 0, \lim_{x \to 0} x^2e^{-1} = e^{-1}·\lim_{x \to 0} x^2 = e^{-1}·0 = 0$ ⇒[By the Squeeze Theorem] $\lim_{x \to 0} x^2·e^{sin(\frac{1}{x})} = 0.$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus.
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
9. blackpenredpen.