Direct & Limit Comparison test

The word ‘politics’ is derived from the word ‘poly’, meaning ‘many’, and the word ‘ticks’, meaning ‘blood-sucking parasites’, Larry Hardiman.

Recall

A finite series is given by all the terms of a finite sequence, added together, e.g., {3, 5, 7, . . . , 21}, $\sum_{k=1}^{10} 2k+1 = 120$. An infinite series is the sum of an infinite sequence of numbers. It is represented in the form $\sum_{n=1}^\infty a_n = a_1 + a_2 + a_3 + ···$ where a_n represents the terms of the sequence, and n is the index that ranges from 1 to infinite.

A series is convergent (or converges) if the sequence of its partial sums tends to a limit, that is, l = $\lim_{n \to ∞} \sum_{k=1}^n a_k$ exists and is a finite number. More precisely, if there exists a number l (or S) such that for every arbitrary small positive number ε, there is a (sufficient large) N, such that ∀n ≥ N, |S_n -l| < ε where S_n = $\sum_{k=1}^n a_k = a_1 + a_2 + ··· + a_n$. If the series is convergent, the number l is called the sum of the series. On the contrary, any series that is not convergent ($\lim_{n \to ∞} \sum_{k=1}^n a_k$ does not exist) is said to be divergent or to diverge.

Divergence Test. If $\lim_{n \to ∞}a_n ≠ 0$, then $\sum_{n=1}^\infty a_n$ diverges.

Integral Comparison. If f(x) is a positive, continuous, and decreasing function on the interval [1, ∞), then $|\sum_{n=1}^\infty f(n) -\int_{1}^{∞} f(x)dx| < f(1).$ Besides, $\sum_{n=1}^\infty f(n)$ converges, if and only if, $\int_{1}^{∞} f(x)dx$ converges.

Theorem (p-series)

Theorem (p-series). A p-series $\sum_{n=1}^\infty \frac{1}{n^p}$ converges if and only if p > 1.

Proof.

If p ≤ 1, the series diverges by comparing it (Direct Comparison Test) with the harmonic series ($n^p ≤ n ⇒\frac{1}{n^p}≥ \frac{1}{n}$) which we already know diverges ($\sum_{n=1}^\infty \frac{1}{n}$ is the harmonic series, and we can use the Integral Test because f(x) = $\frac{1}{x}$ is positive, continuous, and decreasing for x ≥ 1, and $\int_{1}^{∞} \frac{1}{x}dx$ diverges).

Let’s suppose that p > 1. The function f(x) = $\frac{1}{x^p}$ is positive, continuous, and decreasing, so to determine the convergence of the series, we only need to determine the convergence of the corresponding integral.

$\int_{1}^{∞} \frac{1}{x^p}dx = \lim_{b \to ∞} \int_{1}^{b} \frac{1}{x^p}dx = \lim_{b \to ∞} \frac{1}{-p+1}x^{-p+1}= \lim_{b \to ∞} \frac{-1}{(p-1)x^{p-1}}\bigg|_{1}^{b} =$

= $\lim_{b \to ∞} \frac{-1}{(p-1)b^{p-1}}+\frac{1}{(p-1)1^{p-1}} = -0+\frac{1}{p-1} = \frac{1}{p-1}$, so the integral $\int_{1}^{∞} \frac{1}{x^p}dx$ converges ⇒[By the integral comparison test] $\sum_{n=1}^\infty \frac{1}{n^p}$ converges.

Direct Comparison test

Theorem. Direct Comparison test. Let {a_n} and {b_n} be positive sequences where a_n≤b_n ∀n≥N, for some N.

1. If $\sum_{n=1}^\infty b_n$ converges, then $\sum_{n=1}^\infty a_n$ converges.
2. If $\sum_{n=1}^\infty a_n$ diverges, then $\sum_{n=1}^\infty b_n$ converges.

Proof.

a_n, b_n ≥ 0, s_n ≤ s_n + a_n+1 = $\sum_{i=1}^n a_i+a_{n+1} = \sum_{i=1}^n a_{n+1} = S_{n+1}$ ⇒ s_n ≤ s_n+1. With a completely similar argument, both partial sums of {a_n} and {b_n}, let’s name it s_n and t_n respectively, are increasing sequences.

By assumption, a_n ≤ b_n ⇒ s_n ≤ t_n ∀n.

Assume that $\sum_{n=1}^\infty b_n$ converges, s_n ≤ t_n = $\sum_{i=1}^n b_i ≤ \sum_{i=1}^∞ b_i$ ⇒ s_n are abounded about ⇒[If {a_n is bounded and monotonic then {a_n} is convergent.] Monotonic and bonded sequences are convergent, {s_n} is convergent ⇒ $\sum_{n=1}^\infty a_n$ converges.

Next, let’s assume that $\sum_{n=1}^\infty a_n$ diverges ⇒[a_n ≥ 0] s_n → ∞ as n → ∞ ⇒[s_n ≤ t_n ∀n] t_n → ∞ as n → ∞ ⇒ {t_n} is divergent ⇒ $\sum_{n=1}^\infty a_n$ diverges ∎

Limit Comparison Test

Theorem. Limit Comparison Test. Let $\sum_{n=1}^\infty a_n$ and $\sum_{n=1}^\infty b_n$ be positive-termed series. If $\lim_{n \to ∞}\frac{a_n}{b_n}=c,$ where c is finite, c > 0, then either both series converge or both diverge.

Solved exercises

• Determine the convergence of $\sum_{n=1}^\infty \frac{2}{n^3+4}$.

$\sum_{n=1}^\infty \frac{2}{n^3+4} = 2\sum_{n=1}^\infty \frac{1}{n^3+4}$

Besides, ∀n ≥ 1, $\frac{1}{n^3+4}≤\frac{1}{n^3}$, and by the Theorem (p-series) $\sum_{n=1}^\infty \frac{1}{n^3}$ converges (p = 3 > 1) ⇒ By the Direct Comparison Test, $\sum_{n=1}^\infty \frac{1}{n^3+4}$ converges ⇒ $\sum_{n=1}^\infty \frac{2}{n^3+4}$ converges.

• Determine the convergence of $\sum_{n=1}^\infty \frac{2}{n^3-4}$.

It is not true that ∀n ≥ 1, $\frac{1}{n^3-4}≤\frac{1}{n^3}$, but we can understand that both series are quite similar.

$\lim_{n \to ∞} \frac{\frac{2}{n^3-4}}{\frac{1}{n^3}} = \lim_{n \to ∞} \frac{2}{n^3-4}·\frac{n^3}{1} = \lim_{n \to ∞} \frac{2n^3}{n^3-4} = 2 > 1$ ⇒ By the Limit Comparison Test, $\sum_{n=1}^\infty \frac{2}{n^3-4}$ also converges.

• Determine the convergence of $\sum_{n=0}^\infty \frac{1+sin(n)}{10^n}$

Let a_n = $\frac{1+sin(n)}{10^n}$.

-1 ≤ sin(n) ≤ 1 ⇒ 0 ≤ 1 + sin(n) ≤ 2 ⇒ $\frac{0}{10^n}≤\frac{1+sin(x)}{10^n}≤\frac{2}{10^n} ⇒ 0 ≤\frac{1+sin(x)}{10^n}≤\frac{2}{10^n}$. Let b_n = $\frac{2}{10^n},~ \sum_{n=0}^\infty \frac{2}{10^n} = 2·\sum_{n=0}^\infty \frac{1}{10^n}=2·\sum_{n=0}^\infty (\frac{1}{10})^n$ converges (it is a geometric series with r = ¹⁄₁₀ < 1).

$0 ≤ \frac{1+sin(n)}{10^n} ≤ \frac{2}{10^n}$, and $\sum_{n=0}^\infty \frac{2}{10^n}$ converges, then $\sum_{n=0}^\infty \frac{1+sin(n)}{10^n}$ also converges by the Direct Comparison Test.

• Determine the convergence of $\sum_{n=2}^\infty \frac{\sqrt{n}}{n-1}$

Let a_n = $\frac{\sqrt{n}}{n-1}$

$\frac{\sqrt{n}}{n-1}>\frac{\sqrt{n}}{n}=\frac{1}{\sqrt{n}}$.

Let b_n = $\frac{1}{\sqrt{n}}, \sum_{n=2}^\infty \frac{1}{\sqrt{n}}$ diverges by the Theorem (p-series) ⇒ $\sum_{n=2}^\infty \frac{\sqrt{n}}{n-1}$ also diverges by the Direct Comparison test.

• Determine the convergence of $\sum_{n=1}^\infty \frac{\sqrt{n+2}}{2n^2+n+1}$

Consider $\sum_{n=1}^\infty \frac{\sqrt{n}}{n^2} = \sum_{n=1}^\infty \frac{n^{\frac{1}{2}}}{n^2} = \sum_{n=1}^\infty \frac{1}{n^{\frac{3}{2}}}$. By the Theorem (p-series), it converges because ³⁄₂ > 1.

$\lim_{n \to ∞} \frac{\frac{\sqrt{n+2}}{2n^2+n+1}}{\frac{\sqrt{n}}{n^2}} = \lim_{n \to ∞} \frac{\sqrt{n+2}}{2n^2+n+1}·\frac{n^2}{\sqrt{n}} = \lim_{n \to ∞} \sqrt{\frac{n+2}{n}}·\frac{n^2}{2n^2+n+1} = \lim_{n \to ∞} \sqrt{\frac{n+2}{n}}·\lim_{n \to ∞} \frac{n^2}{2n^2+n+1} = 1·\frac{1}{2}=\frac{1}{2} > 0$ ⇒ By the Limit Comparison Test, $\sum_{n=1}^\infty \frac{\sqrt{n+2}}{2n^2+n+1}$ also converges.

• Determine the convergence of $\sum_{n=1}^\infty \frac{9^n}{3+10^n}$.

$\sum_{n=1}^\infty \frac{9^n}{10^n} = \sum_{n=1}^\infty (\frac{9}{10})^n$, this is a geometric series with r = ⁹⁄₁₀ < 1, so it is convergent.

$\lim_{n \to ∞}\frac{\frac{9^n}{3+10^n}}{\frac{9^n}{10^n}}= \lim_{n \to ∞} \frac{9^n}{3+10^n}·\frac{10^n}{9^n} = \lim_{n \to ∞} \frac{10^n}{3+10^n} = \frac{10^n}{10^n} = 1.$ ⇒ By the Limit Comparison Test, $\sum_{n=1}^\infty \frac{9^n}{3+10^n}$ also converges.

• Determine the convergence of $\sum_{n=1}^\infty \frac{1}{3^n+n^2}$.

In this case, let’s compare the given series to $\sum_{n=1}^\infty \frac{1}{3^n}$. This is a convergent geometric series, it converges because ¹⁄₃< 1.

Since $3^n < 3^n + n^2 ⇒ \frac{1}{3^n} > \frac{1}{3^n+n^2}$. The series $\sum_{n=1}^\infty \frac{1}{3^n}$ is a convergent one, then by the Direct Comparison test our original series converges, too.

• Determine the convergence of $\sum_{n=1}^\infty \frac{1}{n-ln(n)}$.

Since ∀n ≥ 1, n ≥ n -ln(n), $\frac{1}{n} ≤ \frac{1}{n-ln(n)}$, and whe know that the harmonic series diverges $\sum_{n=1}^\infty \frac{1}{n}$, so we can conclude by the Direct Comparison test that $\sum_{n=1}^\infty \frac{1}{n-ln(n)}$ diverges.

• Determine the convergence of $\sum_{n=1}^\infty \frac{n3^n}{4n^3+2}$.

The more important element is obviously $\frac{n3^n}{n^3} = \frac{3^n}{n^2}$.

$\lim_{n \to ∞} \frac{3^n}{n^2} = ∞$ ≠ 0. As n approaches infinity, the numerator 3ⁿ grows exponentially. Meanwhile, the denominator n² grows polynomially because it’s a quadratic function ⇒[By the Divergence Test] $\sum_{n=1}^\infty \frac{3^n}{n^2}$ diverges.

$\lim_{n \to ∞} \frac{\frac{n3^n}{4n^3+2}}{\frac{3^n}{n^2}} = \lim_{n \to ∞} \frac{n3^n}{4n^3+2}·\frac{n^2}{3^n} = \lim_{n \to ∞} \frac{n^3}{4n^3+2} = \frac{1}{4} > 0$ ⇒ $\sum_{n=1}^\infty \frac{3^n}{n^2}$ diverges, then $\sum_{n=1}^\infty \frac{n3^n}{4n^3+2}$ also diverges by the Limit Comparison Test.

• Determine the convergence of $\sum_{n=1}^\infty \frac{e^{\frac{1}{n}}}{n}$.

We have previously demonstrated that the harmonic series $\sum_{n=1}^\infty \frac{1}{n}$ diverges.

Besides, $\lim_{n \to ∞} \frac{\frac{e^{\frac{1}{n}}}{n}}{\frac{1}{n}}=\lim_{n \to ∞} \frac{e^{\frac{1}{n}}}{n}·\frac{n}{1} = \lim_{n \to ∞} e^{\frac{1}{n}} = 1 > 0$ ⇒ By the Limit Comparison Test, our original series $\sum_{n=1}^\infty \frac{e^{\frac{1}{n}}}{n}$ diverges.

• Determine the convergence of $\sum_{n=1}^\infty \frac{n}{\sqrt{n^3+n}}$.

It seems obvious to compare it to $\frac{n}{\sqrt{n^3}} = n^{1-\frac{3}{2}} = n^{-\frac{1}{2}} = \frac{1}{n^{\frac{1}{2}}}, \sum_{n=1}^\infty \frac{1}{n^{\frac{1}{2}}}$ diverges (Theorem (p-series), p = ¹⁄₂< 1).

$\lim_{n \to ∞} \frac{\frac{n}{\sqrt{n^3+n}}}{\frac{1}{n^{\frac{1}{2}}}} = \lim_{n \to ∞} \frac{n}{\sqrt{n^3+n}}·\frac{n^{\frac{1}{2}}}{1} = \lim_{n \to ∞} \frac{n^{\frac{3}{2}}}{\sqrt{n^3+n}} = 1 > 0$ (If you don’t see it, divide numerator and denominator by $n^{\frac{3}{2}}$) ⇒ By the Limit Comparison Test, our original series $\sum_{n=1}^\infty \frac{n}{\sqrt{n^3+n}}$ diverges.

• How far out is it possible to overhang blocks from the edge of a table without them toppling?

Rules: No glue! Blocks have to be placed and supported entirely by their own weights. Only one block per level. We’re making a skewed tower. All blocks are of the same shape, weight, and are of uniform density.

The best strategy is a “top-down” approach, that is, to build from the top block down. Let C₀ and C₁ be the left end and the center of mass of the first block (top block) respectively, C₀ = 0, C₁ = 1. Let’s put the second block as far to the right as possible ⇒ its left end is at C1.

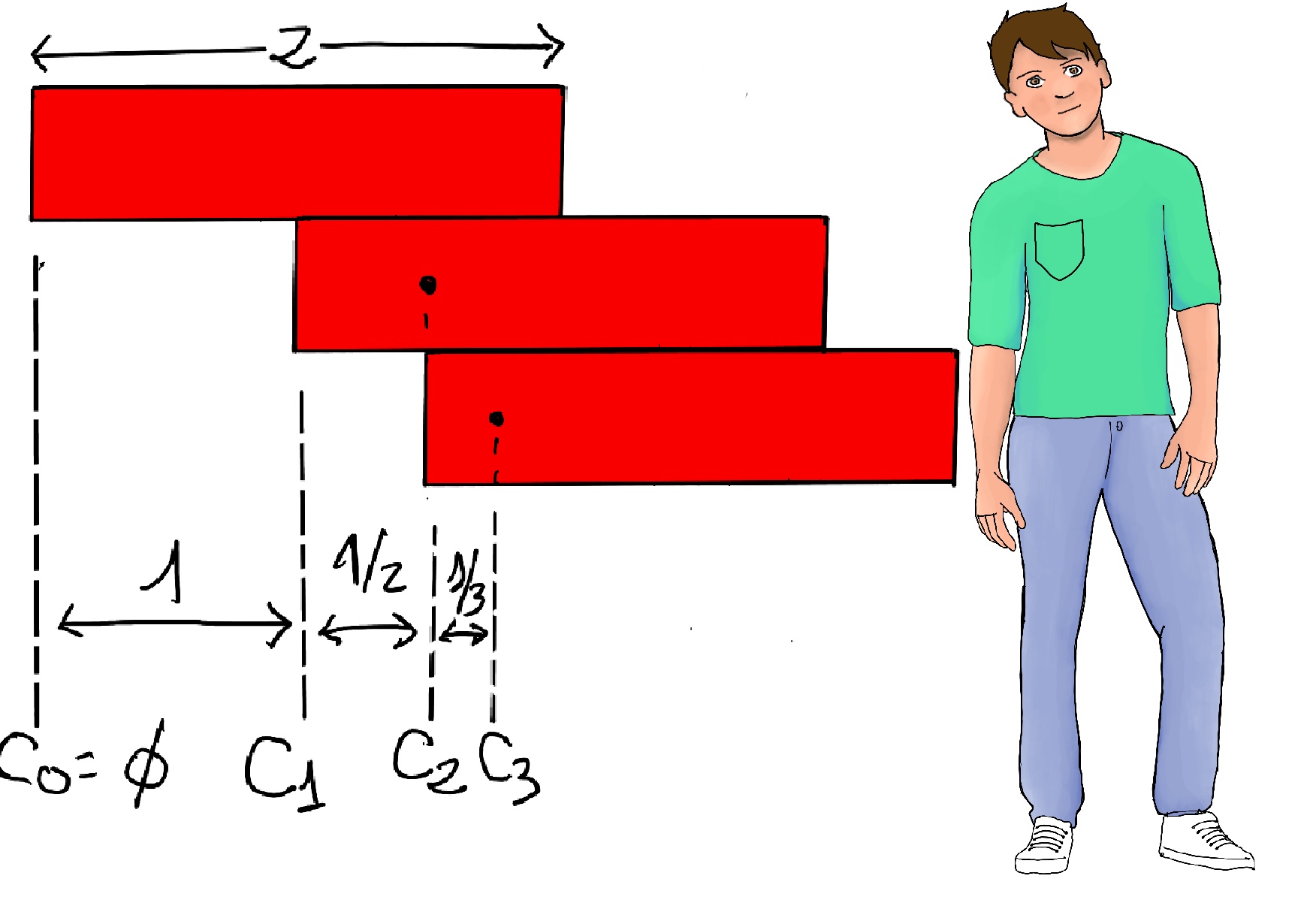
Let C2 be the center of mass of the top two blocks combined (C₂ = 1 + ¹⁄₂). Once again put the left end of the next block underneath the center of mass of all the previous blocks combined (C₃ = 1 + ¹⁄₂ + ¹⁄₃), and in general, $C_{n+1} = \frac{nC_n +1(C_n + 1)}{n + 1}$ [the strategy is to put the left end of the next block underneath the center of mass of all the previous ones combined, namely C_n + 1] = $\frac{(n+1)C_n+1}{n+1} =C_n + \frac{1}{n+1}$.

Recall the Riemann Sum estimation from a previous exercise, ln(N) < S_N < ln(N) + 1 where S_N = C_N = 1 + ¹⁄₂ + ¹⁄₃ + ··· + ¹⁄_N. Sol: You can extend this stack of blocks as far as you want provided that you have enough blocks because ln(N) → ∞ ⇒ S_N → ∞

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus and Calculus 3e (Apex). Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.