Convergence/Divergence of series

There seemed to be some correlation between devotion to God and a misguided zeal for marshmallow, David Sedaris.

Recall

A finite series is given by all the terms of a finite sequence, added together, e.g., {3, 5, 7, . . . , 21}, $\sum_{k=1}^{10} 2k+1 = 120$. An infinite series is the sum of an infinite sequence of numbers. It is represented in the form $\sum_{n=1}^\infty a_n = a_1 + a_2 + a_3 + ···$ where a_n represents the terms of the sequence, and n is the index that ranges from 1 to infinite.

A series is convergent (or converges) if the sequence of its partial sums tends to a limit, that is, l = $\lim_{n \to ∞} \sum_{k=1}^n a_k$ exists and is a finite number. More precisely, if there exists a number l (or S) such that for every arbitrary small positive number ε, there is a (sufficient large) N, such that ∀n ≥ N, |S_n -l| < ε where S_n = $\sum_{k=1}^n a_k = a_1 + a_2 + ··· + a_n$. If the series is convergent, the number l is called the sum of the series. On the contrary, any series that is not convergent ($\lim_{n \to ∞} \sum_{k=1}^n a_k$ does not exist) is said to be divergent or to diverge.

Necessary condition for the convergence of a series

Consider $\sum_{n=1}^\infty \frac{1}{n}$. Taking the upper Riemann sum (Δx = 1), $\int_{1}^{N} \frac{dx}{x} < 1 + \frac{1}{2} + \frac{1}{3} + ··· + \frac{1}{N-1}$ <[S_n has one more term, namely ¹⁄_N] S_N.

Besides, $\int_{1}^{N} \frac{dx}{x} = ln(x)\bigg|_{1}^{N} = ln(N)$ ⇒ ln(N) < S_n (Figure 2.1).

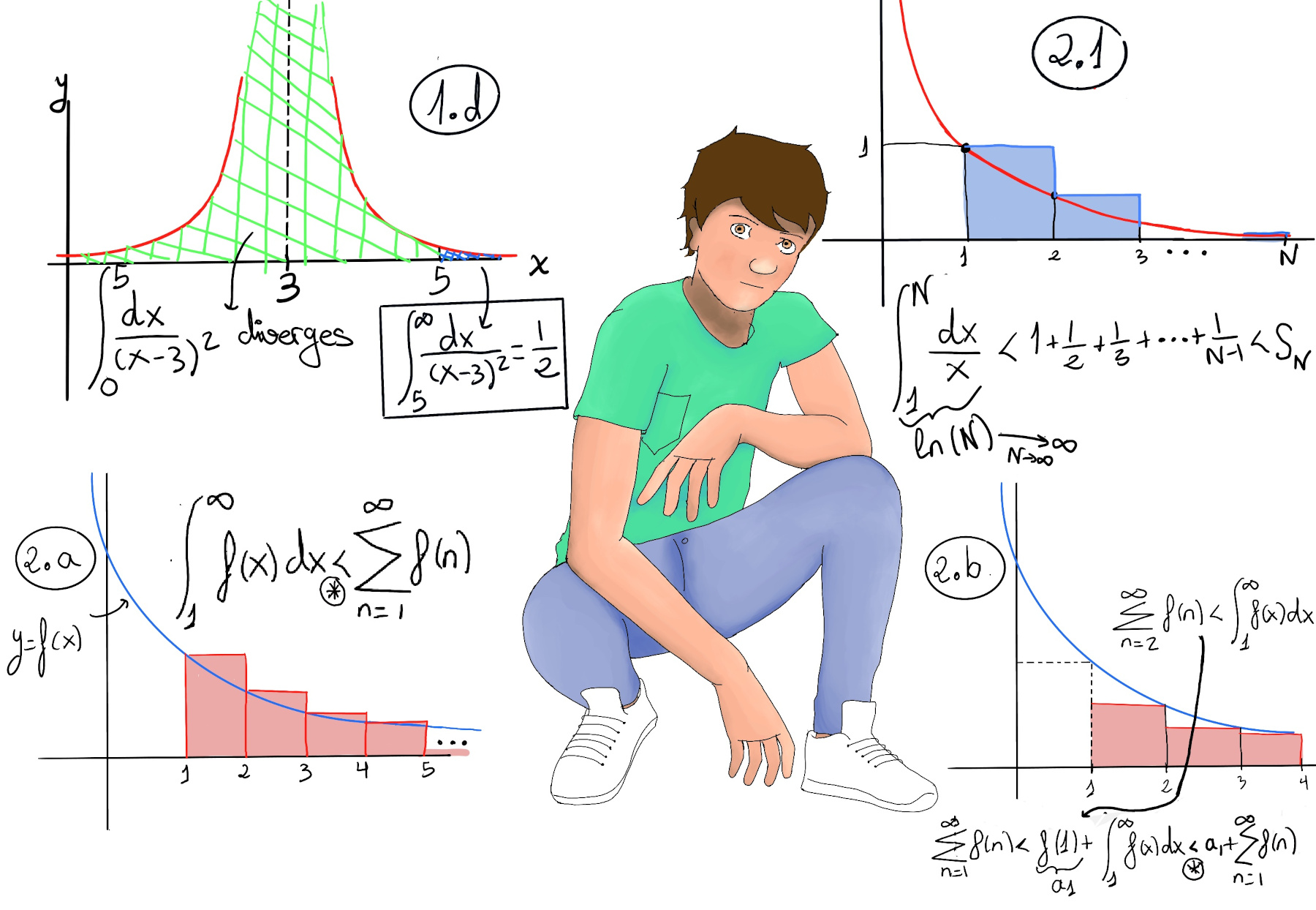
Futhermore, we know that $\lim_{N \to ∞}ln(N) = ∞$, hence $\lim_{N \to ∞}S_N = ∞$ ⇒ $\sum_{n=1}^\infty \frac{1}{n}$ diverges.

Taking the lower Riemann Sum (Δx = 1), $\int_{1}^{n} \frac{dx}{x} > \frac{1}{2} + \frac{1}{3} + ··· + \frac{1}{N} = S_N -1$ ⇒ ln(N) < S_N < ln(N) + 1. We can generalize this result in the following proposition.

Necessary condition for the convergence of a series. If $\sum_{n=1}^\infty a_n$ converges, then $\lim_{n \to ∞}a_n = 0$ In words, in order for a series to converge the series terms must go to zero in the limit.

Proof.

a_n = s_n -s_n-1. Besides, if $\sum_{n=1}^\infty a_n$ converges ⇒ $\sum_{n=1}^\infty s_n$ is also convergent for some value s ↭ $\lim_{n \to \infty} s_n = s$ ⇒ $\lim_{n \to \infty} s_{n-1} = s$ ⇒ $\lim_{n \to ∞}a_n = \lim_{n \to ∞} s_n - s_{n-1} = \lim_{n \to ∞} s_n - \lim_{n \to ∞} s_{n-1} = s -s = 0$.

Divergence Test. If $\lim_{n \to ∞}a_n ≠ 0$, then $\sum_{n=1}^\infty a_n$ diverges. In words, if the series terms do not go to zero in the limit then the series diverges.

Solved examples

• Be cautious!💀 This result gives us a necessary condition or requirement for convergence but it is not a guarantee of convergence. The series terms of $\sum_{n=1}^\infty \frac{1}{n}$ and $\sum_{n=1}^\infty \frac{1}{n^2}$ are zero in the limit as n goes to infinity, yet only the second series converges.

• $\sum_{n=1}^\infty \frac{4n+1}{5n-7}$ diverges by the Divergence Test since $\lim_{n \to ∞} a_n = \lim_{n \to ∞} \frac{4n+1}{5n-7} =$[L’Hôpital, ∞/∞] $\frac{4}{5} ≠ 0.$

• $\sum_{n=1}^\infty 3^n$ diverges by the Divergence Test since $\lim_{n \to ∞} a_n = \lim_{n \to ∞} 3^n = ∞ ≠ 0.$

• $\sum_{n=1}^\infty cos(\frac{1}{n^2})$ diverges by the Divergence Test since $\lim_{n \to ∞} a_n = \lim_{n \to ∞} cos(\frac{1}{n^2}) = cos(0) = 1 ≠ 0.$

Integral Comparison

Integral Comparison. If f(x) is a positive, continuous, and decreasing function on the interval [1, ∞), then $|\sum_{n=1}^\infty f(n) -\int_{1}^{∞} f(x)dx| < f(1).$ Besides, $\sum_{n=1}^\infty f(n)$ converges, if and only if, $\int_{1}^{∞} f(x)dx$ converges.

Proof.

Using the same argument (upper Riemann sum, the rectangles enclose more area than the area under f(x)), $\int_{1}^{∞} f(x)dx < \sum_{n=1}^\infty f(n)$ (Figure 2.a), and $\sum_{n=2}^\infty f(n) < \int_{1}^{∞} f(x)dx$ (Figure 2.b., the areas of the rectangles is less than the area under f(x), but this summation starts with n = 2) ⇒ $\sum_{n=1}^\infty f(n) < a_1 + \int_{1}^{∞} f(x)dx$ where a₁ = f(1).

Combining both equations, $\sum_{n=1}^\infty f(n) <[Inequality~ i] a_1 + \int_{1}^{∞} f(x)dx <[Inequality~ ii] a_1 + \sum_{n=1}^\infty f(n)$ ⇒ $|\sum_{n=1}^\infty f(n) -\int_{1}^{∞} f(x)dx| < f(1).$

Notice that $\sum_{n=1}^\infty f(n) < a_1 + \int_{1}^{∞} f(x)dx ⇒ \sum_{n=1}^\infty f(n) - \int_{1}^{∞} f(x)dx < a_1$. Besides, $a_1 + \int_{1}^{∞} f(x)dx < a_1 + \sum_{n=1}^\infty f(n) ⇒ \sum_{n=1}^\infty f(n) - \int_{1}^{∞} f(x)dx > (a_1-a_1=)~ 0 ≥ -a_1,$ because f is positive f(1) = a₁≥ 0.

If $\sum_{n=1}^\infty f(n)$ diverges, so does $\int_{1}^{∞} f(x)dx$ because $\sum_{n=1}^\infty f(n) < a_1 + \int_{1}^{∞} f(x)dx$ (i). If $\int_{1}^{∞} f(x)dx$ diverges, so does $\sum_{n=1}^\infty f(n)$ because $\int_{1}^{∞} f(x)dx < \sum_{n=1}^\infty f(n)$

If $\sum_{n=1}^\infty f(n)$ converges, so does $\int_{1}^{∞} f(x)dx$ because $\int_{1}^{∞} f(x)dx < \sum_{n=1}^\infty f(n)$. If $\int_{1}^{∞} f(x)dx$ converges, so does $\sum_{n=1}^\infty f(n)$ because $\sum_{n=1}^\infty f(n) < a_1 + \int_{1}^{∞} f(x)dx$

A generalized version is this theorem. If f(x) is a positive, continuous, and decreasing function on the interval [k, ∞), and that f(n) = a_n, then $\sum_{n=k}^\infty a_n$ and $\int_{k}^{∞} f(x)dx$ either both converge or both diverge.

1. If $\sum_{n=k}^\infty a_n$ diverges, so does $\int_{k}^{∞} f(x)dx$. If $\sum_{n=k}^\infty a_n$ converges, so does $\int_{1}^{∞} f(x)dx$.
2. If $\int_{k}^{∞} f(x)dx$ diverges, so does $\sum_{n=k}^\infty a_n$. If $\int_{1}^{∞} f(x)dx$ converges, so does $\sum_{n=k}^\infty a_n$.

Solved examples

• $\sum_{n=1}^\infty \frac{2}{3n+5}$.

First, we must check the conditions before applying the integral test ∀x ≥ 1, f(x) = $\frac{2}{3x+5}$ is…

1. Positive.
2. Continuous. It is a rational function. A rational function is continuous for all x except those values that make a denominator 0 ↭ 3x + 5 = 0 ↭ x = ^-5⁄₃∉ [1, ∞).
3. Decreasing. f’(x) = $(-2)(3x+1)^{-2}·3 = \frac{-6}{(3x+1)^2}< 0 ⇒ f$ is always decreasing.
4. $\int_{1}^{∞} \frac{2}{3x+5}dx = $[U-substitution, 3x + 5 = u ⇒ 3dx = du] $\frac{2}{3}\int_{1}^{∞} \frac{du}{u} = \lim_{b \to ∞} \frac{2}{3}\int_{1}^{b} \frac{du}{u} = \lim_{b \to ∞} \frac{2}{3}·ln|u| = \lim_{b \to ∞} \frac{2}{3}·ln|3x+5|\bigg|_{1}^{b}=$

$\lim_{b \to ∞} \frac{2}{3}·(ln(3b+5)-ln(8)) = ∞$⇒ our original integral diverges.

• $\sum_{n=1}^\infty \frac{1}{2^n}$

First, we must check the conditions before applying the integral test ∀x ≥ 1, f(x) = $\frac{1}{2^x}$ is…

1. Positive.
2. Continuous. It is a rational function. A rational function is continuous for all x except those values that make a denominator 0, and 2^x ≠ 0 ∀x ≥ 1.
3. Decreasing. f’(x) = $-(ln(2))2^{-x} = \frac{-ln(2)}{2^x}< 0 ⇒ f$ is always decreasing ∀x ≥ 1.
4. $\int_{1}^{∞} \frac{1}{2^x}dx =\int_{1}^{∞} 2^{-x}dx =[Recall~\int a^xdx=\frac{a^x}{ln(a)}] \lim_{b \to ∞} \frac{-1}{(ln(2))2^x}\bigg|_{1}^{b}=$

$=\lim_{b \to ∞} \frac{-1}{ln(2)2^b}+\frac{1}{ln(2)2^1} = 0 + \frac{1}{2ln(2)} = \frac{1}{2ln(2)}$ ⇒ our original integral converges.

• $\sum_{n=1}^\infty \frac{ln(n)}{n^2}$.

Check conditions: f(x) = $\frac{ln(x)}{x^2}$ is positive, continuos, and decreasing on the interval [2, ∞). First, we know that f(x) is positive and continuous as both ln(n) and n² are positive and continuous on the interval [2, ∞). f’(x) = $\frac{x-2x·ln(x)}{x^4} = \frac{1-2ln(x)}{x^3}$.

x ≥ 2 ⇒[We indeed only need x ≥ $e^{\frac{1}{2}}$ ≈ 1.65] ln(x) ≥ ¹⁄₂ ⇒ 2ln(x) ≥ 1 ⇒ 1 -2ln(x) ≤ 0 ⇒ ∀x ≥ 2, f’(x) ≤ 0 ⇒ ∀x ≥ 2, f is decreasing.

Integral test: $\int_{1}^{∞} \frac{ln(x)}{x^2}dx = \lim_{a \to ∞} \int_{1}^{a} \frac{ln(x)}{x^2}dx =$ [Integration by parts, u = ln(x), dv = ^dx⁄_x², du = ^dx⁄_x, v = ^-1⁄_x] = [1] + [2]

[1] = $\lim_{a \to ∞} -\frac{ln(x)}{x}\bigg|_{1}^{a}$ =

$\lim_{a \to ∞} -\frac{ln(a)}{a} +ln(1) = \lim_{a \to ∞} -\frac{ln(a)}{a}$ [Let’s apply L’Ho^pital’s Rule] $\lim_{a \to ∞} -\frac{\frac{1}{a}}{1} = \lim_{a \to ∞} -\frac{1}{a} = 0$

[2] = $\lim_{a \to ∞} \int_{1}^{a} \frac{1}{x^2} dx = \lim_{a \to ∞}-\frac{1}{x}\bigg|_{1}^{a} = \frac{-1}{a}+1$ → 1 when a → ∞.

Therefore, $\int_{1}^{∞} \frac{ln(x)}{x^2}dx$ = [1] + [2] = 0 + 1 = 1, since the integral converges, the series converges.

• $\sum_{n=1}^\infty \frac{2}{n^2+6n+10} = \sum_{n=1}^\infty \frac{2}{(n+3)^2+1}$.

Check conditions: f(x) = $\frac{2}{(x+3)^2+1}$ is positive, continuos (It is a rational function. A rational function is continuous for all x except those values that make a denominator 0), and decreasing on the interval [2, ∞) ((x+3)²+1 is a parabola with a minimum at (-3, 1) ⇒ $\frac{1}{(x+3)^2+1}$ is decreasing on the interval (-3, ∞), the constant 2 does not make any difference.

$\int_{1}^{∞} \frac{2}{(x+3)^2+1}dx$ [x+3 = tan(θ), dx = sec²(θ)dθ] $\int_{1}^{∞} \frac{2}{(tan(θ))^2+1}sec^2(θ)dθ = \int_{1}^{∞} \frac{2}{sec^2(θ)}sec^2(θ)dθ = \lim_{b \to ∞} \int_{1}^{b} 2dθ = \lim_{b \to ∞} 2θ = \lim_{b \to ∞} 2tan^{-1}(x+3)\bigg|_{1}^{b} =$

$\lim_{b \to ∞} 2tan^{-1}(b+3)-2tan^{-1}(4) = 2\frac{π}{2}-2tan^{-1}(4) = π - 2arctan(4)$, since the integral converges, the series converges.

• $\sum_{n=1}^\infty \frac{e^{\frac{1}{n}}}{n^2}$.

Check conditions: f(x) = $\frac{e^{\frac{1}{x}}}{x^2}$ is positive, continuos (it is only discontinuous at x = 0), and decreasing on the interval [1, ∞)

f’(x) = $\frac{x^2e^{\frac{1}{x}}\frac{-1}{x^2}-2x·e^{\frac{1}{x}}}{x^4} = \frac{-e^{\frac{1}{x}}-2x·e^{\frac{1}{x}}}{x^4}=\frac{-e^{\frac{1}{x}}(1+2x)}{x^4} ≤ 0$ ∀x ∈ [1, ∞) ⇒ f is decreasing on [1, ∞).

$\int_{1}^{∞} \frac{e^{\frac{1}{x}}}{x^2}dx =$[$u = \frac{1}{x}, du = \frac{-1}{x^2}dx$] $\int_{1}^{∞} -e^udu = \lim_{b \to ∞} -e^u = \lim_{b \to ∞} -e^{\frac{1}{x}}\bigg|_{1}^{b} =$

= $\lim_{b \to ∞} -e^{\frac{1}{b}}+e^{\frac{1}{1}}=-1+e$, since the integral converges, the series converges.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus and Calculus 3e (Apex). Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.