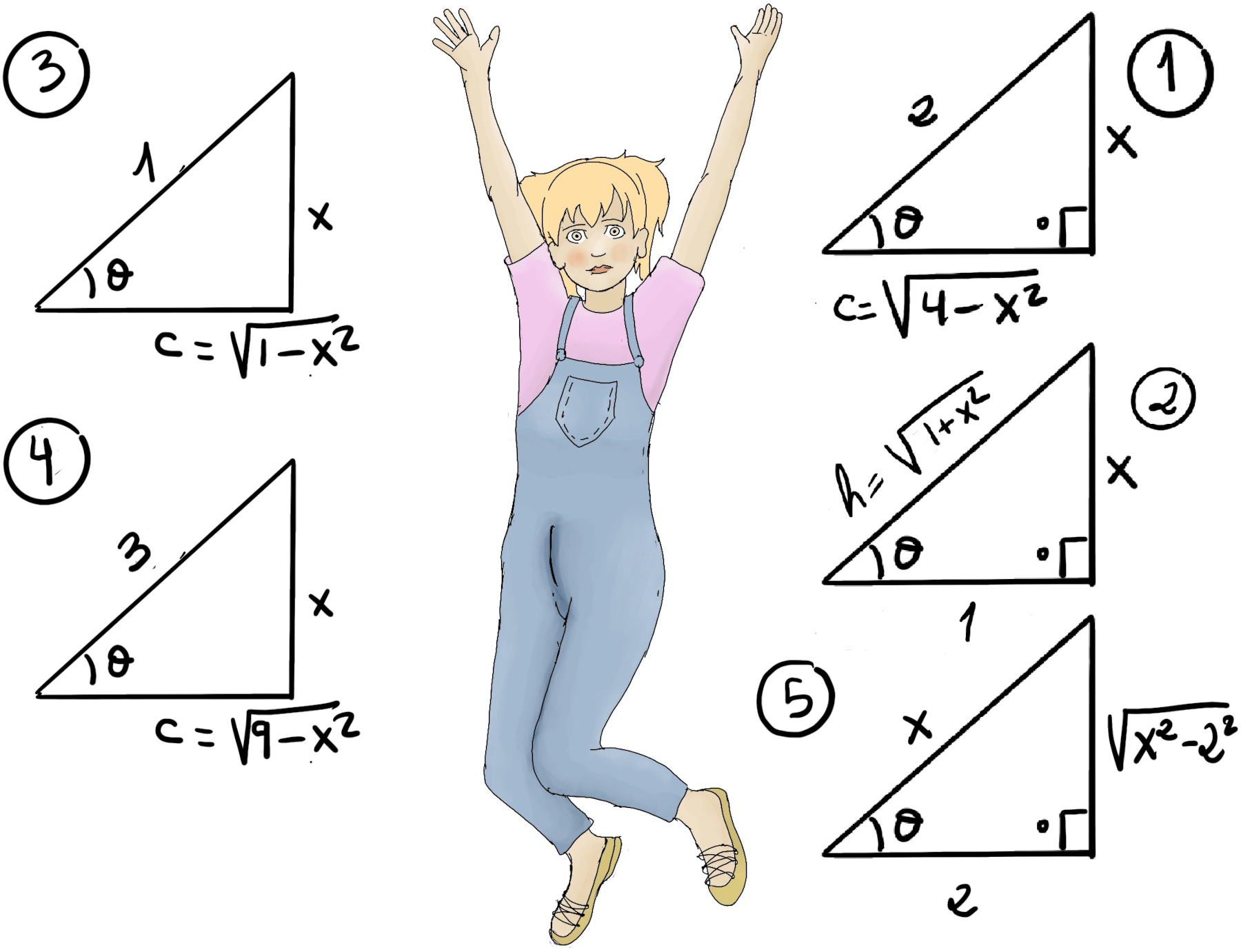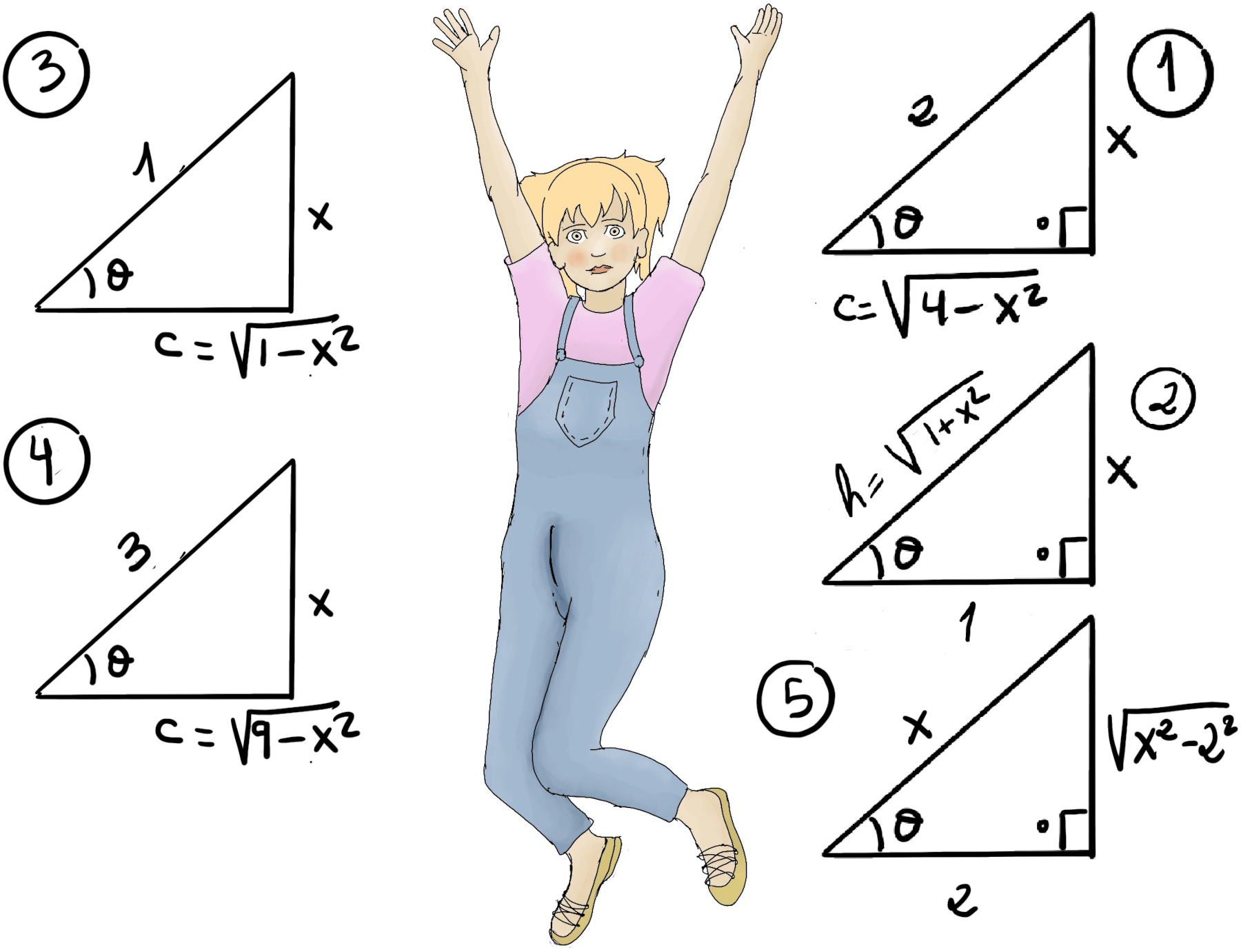Integration of Trigonometric Functions II

Reality has a bad habit of massacring beautiful and carefully constructed fantasies, but the world is relentless and cruel, and dreams are just dreams; in other words, dreams need to be based upon something realistically possible, that is, taking into consideration your age, knowledge, talents, health, economical and social circumstances, and the social and economic environment where you are present, JustToThePoint, Anawim, #justtothepoint.

Recall

In calculus, an antiderivative or indefinite integral, G, of a function g, is the function that can be differentiated to obtain the original function, that is, G’ = f.

G(x) = $\int f(x)dx$

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles.

This is the second article in our two-part series about Integration of Trigonometric Functions and is a continuation of the first one, so if you haven’t taken a look at it yet, I recommend you read it first and come back.

Solved examples

• $\int \frac{dx}{x^2\sqrt{x^2+4}}$ =[Trigonometric substitution, x = 2tan(θ), dx = 2sec²(θ)dθ] $\int \frac{2sec^2(θ)dθ}{4tan^2(θ)\sqrt{4tan^2(θ)+4}} = \int \frac{sec^2(θ)dθ}{4·tan^2(θ)\sqrt{tan^2(θ)+1}} = $[Recall that sec²(x)=1+tan²(x)] $\int \frac{sec^2(θ)dθ}{4·tan^2(θ)\sqrt{sec^2(θ)}} = \int \frac{sec(θ)dθ}{4·tan^2(θ)} = \frac{1}{4}\int \frac{1}{cos(θ)}\frac{cos^2(θ)}{sin^2(θ)}dθ = \frac{1}{4}\int \frac{cos(θ)}{sin^2(θ)}dθ$ =[Derivatives of Trigonometric Formulas, csc’(θ) = -csc(θ)cot(θ) = $-\frac{1}{sin(θ)}·\frac{1}{tan(θ)}=-\frac{1}{sin(θ)}\frac{cos(θ)}{sin(θ)} = \frac{-cos(θ)}{sin^2(θ)}$] = $-\frac{csc(θ)}{4}+C.$

• $\int \frac{\sqrt{x^2-4}}{x^4}dx$ [Trigonometric substitution, think about $x^2-4=x^2-2^2$, so it needs to be a right triangle’s leg, Figure 5, x = 2sec(θ), dx = 2sec(θ)tan(θ)dθ] = $\int \frac{\sqrt{4sec^2(θ)-4}}{(2sec(θ))^4}2sec(θ)tan(θ)dθ = \int \frac{\sqrt{4(sec^2(θ)-1)}}{16sec^4(θ)}2sec(θ)tan(θ)dθ = \frac{1}{4}\int \frac{\sqrt{sec^2(θ)-1}}{sec^4(θ)}sec(θ)tan(θ)dθ$ =[Recall sec²(x) = 1 + tan²(x)] $\frac{1}{4}\int \frac{\sqrt{tan^2(θ)}}{sec^4(θ)}sec(θ)tan(θ)dθ = \frac{1}{4}\int \frac{tan(θ)}{sec^4(θ)}sec(θ)tan(θ)dθ = \frac{1}{4}\int \frac{tan^2(θ)}{sec^3(θ)}dθ = \frac{1}{4}\int tan^2(θ)·cos^3(θ)dθ = \frac{1}{4}\int \frac{sin^2(θ)}{cos^2(θ)}·cos^3(θ)dθ = \frac{1}{4}\int sin^2(θ)·cos(θ)dθ$ =[Integration substitution u = sin(θ), du = cos(θ)dθ] $\frac{1}{4}\int u^2du = \frac{1}{4}\frac{1}{3}u^3 = \frac{1}{12}sin^3(θ)$ =[Backtrack our substitution, Figure 5, sin(θ) = $\frac{\sqrt{x^2-4}}{x}$] $\frac{1}{12}(\frac{(\sqrt{x^2-4})^3}{x^3}) = \frac{(x^2-4)^{\frac{3}{2}}}{12x^3}+C$

• Let’s compute the area of the section inside the circle with radius a and height b (Figure 1.a.).

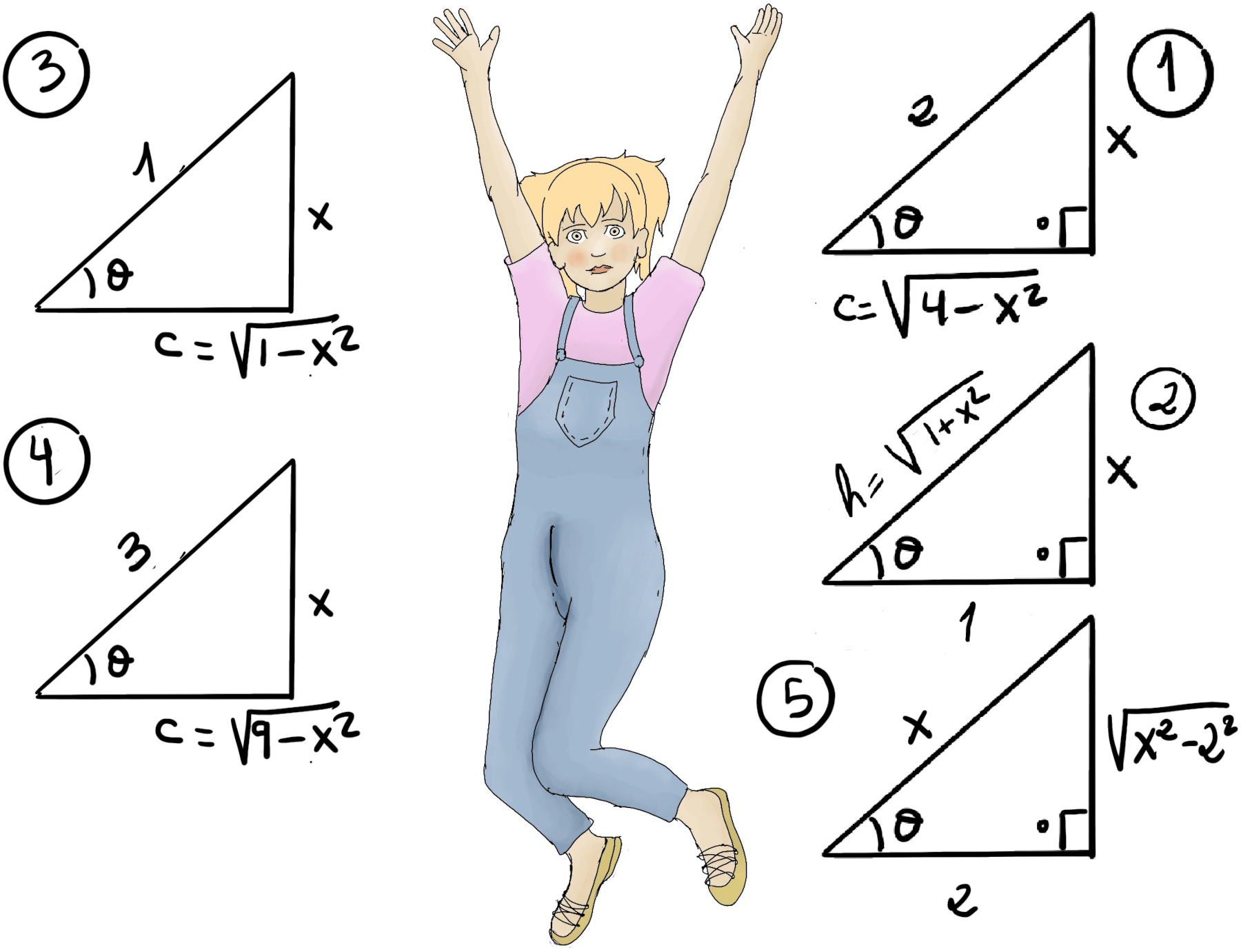
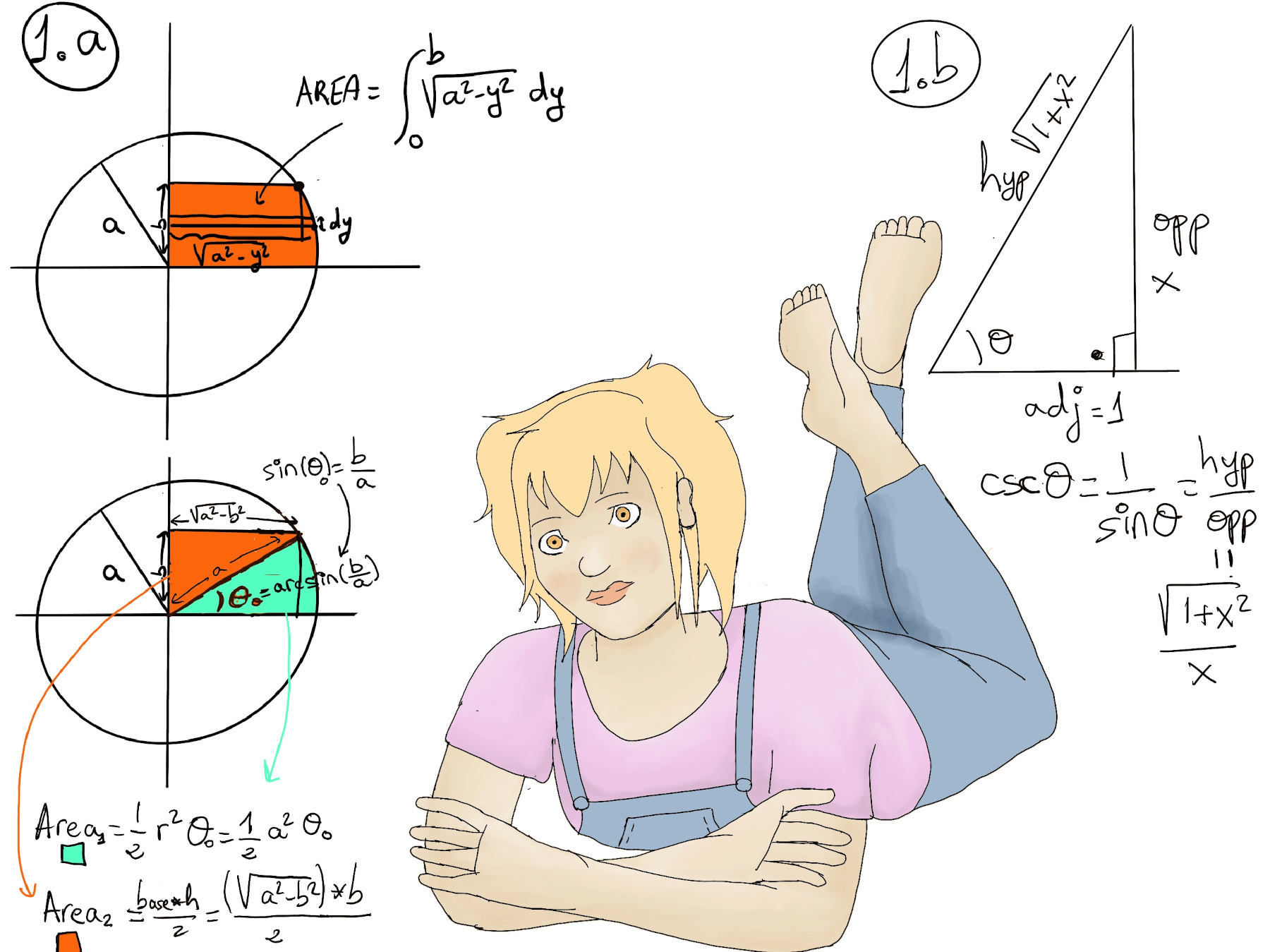
Area = $\int_{0}^{b} \sqrt{a^2-y^2}dy$ =[Trigonometric substitution, y = asin(θ), $\sqrt{a^2-y^2} = \sqrt{a^2-a^2sin^2(θ)} = a\sqrt{1-sin^2(θ)} = a\sqrt{cos^2(θ)}$ = acos(θ) = x, dy = acos(θ)dθ] $\int_{0}^{b} acos(θ)(acos(θ)dθ) = a^2\int cos^2(θ)dθ =$[It was previously calculated] $a^2(\frac{θ}{2}+\frac{sin(2θ)}{4}) = a^2(\frac{θ}{2}+\frac{sin(θ)cos(θ)}{2})$ = [sin(θ) = ^y⁄_a ⇒ θ = arcsin(^y⁄_a)]$\frac{a^2arcsin(y/a)}{2}+ \frac{y(\sqrt{a^2-y^2})}{2}\bigg|_{0}^{b} = \frac{a^2arcsin(b/a)}{2}+ \frac{b(\sqrt{a^2-b^2})}{2} = \frac{a^2θ_0}{2}+ \frac{b(\sqrt{a^2-b^2})}{2} $ where $θ_0 = arcsin(\frac{b}{a})$.

Geometric interpretation. If you have a circle with radius r and a central angle θ (measured in radians), the area of the sector, aka Area₁, is given by $\frac{1}{2}r^2θ = \frac{1}{2}a^2θ_0$. Area₂ = $\frac{b(\sqrt{a^2-b^2})}{2}$ is the area of the upper triangle.

• $\int \frac{\sqrt{4-x^2}}{x^2}dx$ =[Trigonometry substitution, x = 2sin(θ), dx = 2cos(θ)dθ] $\int \frac{\sqrt{4-4sin^2(θ)}}{4sin^2(θ)}2cos(θ)dθ = \int \frac{\sqrt{4(1-sin^2(θ))}}{4sin^2(θ)}2cos(θ)dθ = \int \frac{\sqrt{4(cos^2(θ))}}{4sin^2(θ)}2cos(θ)dθ = \int \frac{2cos(θ)}{4sin^2(θ)}2cos(θ)dθ = \int \frac{cos^2(θ)}{sin^2(θ)}dθ = \int \frac{1-sin^2(θ)}{sin^2(θ)}dθ = \int \frac{1}{sin^2(θ)}dθ - \int dθ = \int csc^2(θ)dθ - \int dθ$ =[Derivate of Trigonometric Formulas, cot’(x) = -csc²(x)] -cot(θ) -θ +C.

Now, we need to backtrack our substitution (Figure 1), $x = 2sin(θ) ⇒ sin(θ)=\frac{x}{2}.$ By the Pythagorean theorem, $c^2+x^2 = 2 ⇒c = \sqrt{4-x^2}$. Besides, $tan(θ)=\frac{x}{\sqrt{4-x^2}}, cot(θ)=\frac{1}{tan(θ)} = \frac{\sqrt{4-x^2}}{x}, \int \frac{\sqrt{4-x^2}}{x^2}dx = -cot(θ) -θ +C = -\frac{\sqrt{4-x^2}}{x}-sin^{-1}(\frac{x}{2})+C.$

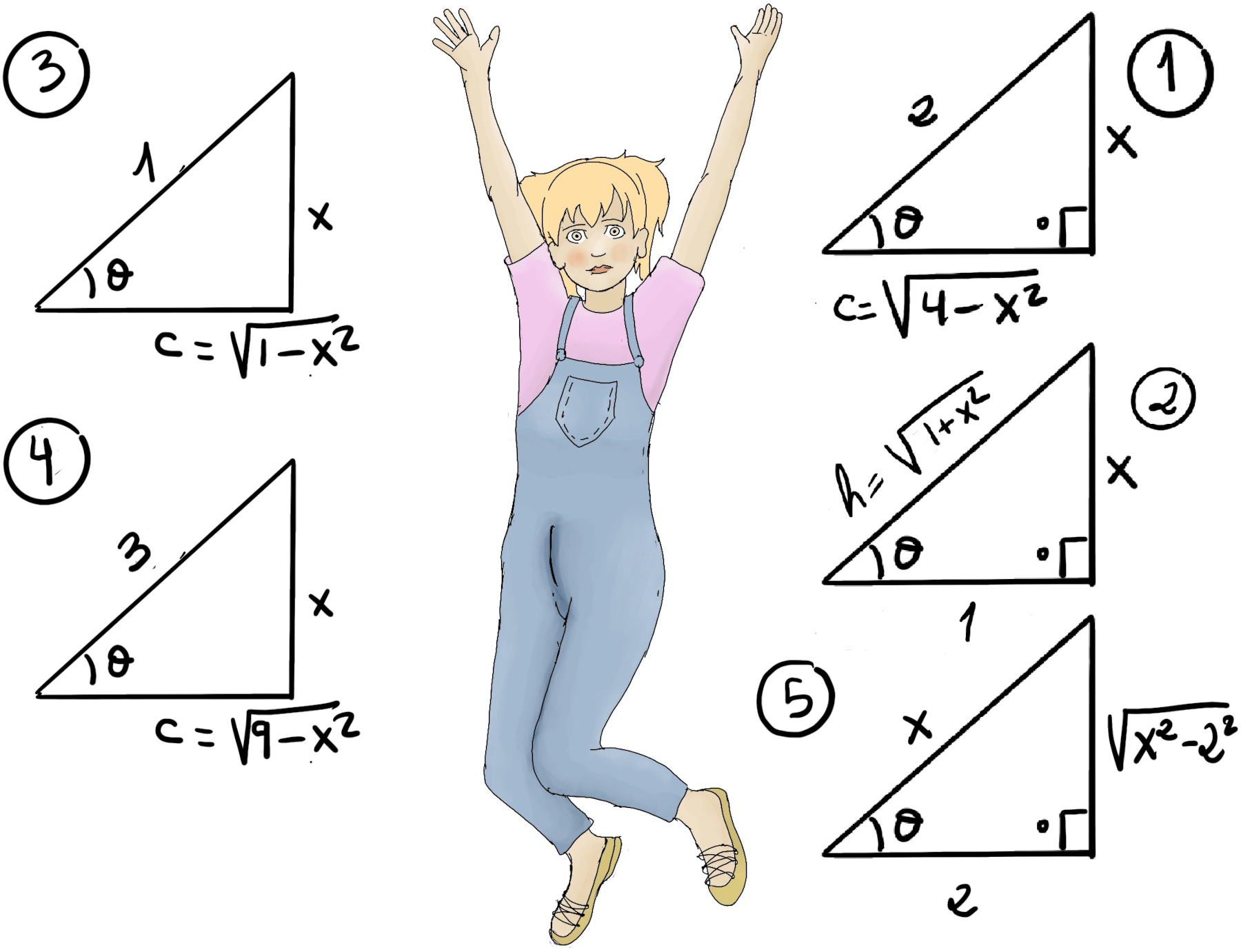
• $\int sec^4(x)dx$ =[Recall sec²(x) = 1 + tan²(x)] $\int (1 + tan^2(x))sec^2(x)dx$ [Apply substitution, u = tan(x), du = sec²(x)dx] $\int (1 + u^2)du = u + \frac{u^3}{3} + C = tan(x) + \frac{tan^3(x)}{3} + C.$

• $\int \frac{dx}{x^2\sqrt{1+x^2}}$ [Recall that sec²(x) = 1 + tan²(x), let’s apply substitution x = tan(θ), 1 + x² = sec²(θ), dx = sec²(θ)dθ] $\int \frac{sec^2(θ)dθ}{(tan(θ))^2sec(θ)} = \int \frac{sec(θ)dθ}{(tan(θ))^2} = \int \frac{cos^2(θ)dθ}{cos(θ)sin^2(θ)} = \int \frac{cos(θ)dθ}{sin^2(θ)}$ [u = sin(θ), du = cos(θ)dθ] $\int \frac{du}{u^2} = \frac{-1}{u} + C = \frac{-1}{sin(θ)} + C = -csc(θ) + C$ [Figure 1.b.] = $-\frac{\sqrt{1+x^2}}{x}+C$

• $\int \frac{x^2}{\sqrt{9-x^2}}dx$ [Trigonometric Substitution, 💡$\sqrt{3^2-3^2sin^2(θ)}$, x = 3·sin(θ), dx = 3cos(θ)dθ]= $\int \frac{(3·sin(θ))^2}{\sqrt{3^2-3^2sin^2(θ)}}3cos(θ)dθ = \int \frac{9·sin^2(θ)}{3\sqrt{1-sin^2(θ)}}3cos(θ)dθ = \int \frac{9·sin^2(θ)}{\sqrt{1-sin^2(θ)}}cos(θ)dθ = \int \frac{9·sin^2(θ)}{\sqrt{cos^2(θ)}}cos(θ)dθ = 9\int sin^2(θ)dθ$ =[Half-Angle Formulas] $9\int \frac{1}{2}(1-cos(2θ))dθ = \frac{9}{2}\int (1-cos(2θ))dθ = \frac{9}{2}(θ-\frac{1}{2}sin(2θ)) =$[Double Angle Formulas, sin(2θ) = 2sin(θ)cos(θ)] $\frac{9}{2}(θ-sin(θ)cos(θ))$

Now, we need to backtrack our substitution (Figure 4), x = 3sin(θ) ⇒ $sin(θ)=\frac{x}{3}, θ = sin^{-1}(\frac{x}{3}), cos(θ)=\frac{\sqrt{9-x^2}}{3} ⇒ \int \frac{x^2}{\sqrt{9-x^2}}dx = \frac{9}{2}(θ-sin(θ)cos(θ)) = \frac{9}{2}(sin^{-1}(\frac{x}{3})-\frac{x}{3}\frac{\sqrt{9-x^2}}{3}) = \frac{9}{2}(sin^{-1}(\frac{x}{3})-\frac{x\sqrt{9-x^2}}{9})+C.$

• $\int_{1}^{\sqrt{3}} \frac{1}{(1+x^2)^{\frac{3}{2}}}dx = \int_{1}^{\sqrt{3}} \frac{1}{(\sqrt{1+x^2})^3}dx$= [Trigonometric substitution, x = tan(θ), Figure 2, dx = sec²(θ)dθ, $x = \sqrt{3} ⇒ tan(θ) = \sqrt{3} ⇒ θ = tan^{-1}(\sqrt{3}) = \frac{π}{3}, x = 1 ⇒ tan(θ) = 1 ⇒ θ = tan^{-1}(1) = \frac{π}{4}$] $\int_{\frac{π}{4}}^{\frac{π}{3}} \frac{1}{(\sqrt{1+tan^2(θ)})^3}sec^2(θ)dθ$ =[Recall sec²(x) = 1 + tan²(x)] $\int_{\frac{π}{4}}^{\frac{π}{3}} \frac{1}{(\sqrt{sec^2(θ)})^3}sec^2(θ)dθ = \int_{\frac{π}{4}}^{\frac{π}{3}} \frac{1}{sec^3(θ)}sec^2(θ)dθ = \int_{\frac{π}{4}}^{\frac{π}{3}} \frac{1}{sec(θ)}dθ = \int_{\frac{π}{4}}^{\frac{π}{3}} cos(θ)dθ = sin(θ)\bigg|_{\frac{π}{4}}^{\frac{π}{3}} = sin(\frac{π}{3})-sin(\frac{π}{4}) = \frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2} = \frac{\sqrt{3}-\sqrt{2}}{2}$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
10. Professor Leonard.