Integral domains.

“Mmm, what do we really know?” Apathicus consulted the big encyclopedia once again. “We know very little indeed. What happens when we die? Do we reincarnate as angry hyppos? Does dark matter really matter? Are we living in a simulation? Can we complain to the manager?…” Apocalypse, Anawim, #justtothepoint.

Recall

Definition. A zero-divisor is an non-zero element a of a commutative ring R such that there exist a nonzero element in the ring, say b ∈ R with ab = 0, e.g., 2, 3, 4, 6, 8, 9, and 10 are zero divisors in ℤ₁₂, 4·3 =_ℤ12 0, even though 4 and 3 are nonzero elements in ℤ₁₂.

Zero divisors do not have inverses. Proof: Suppose for the sake of contradiction there are two elements a, b ∈ R with a, b ≠ 0, ab = 0, aa^-1 = a^-1a = 1. a^-1ab =[Associativity] (a^-1a)b = 1·b = b. a^-1ab =[Associativity] a^-1(ab) = a^-1·0 = 0 ⊥

m ∈ ℤ_n is a zero divisor ↭ m do no have inverses ↭ gcd(m, n) ≠ 1. In ℤ₂₄: [24 = 2³·3] 2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, e.g., 2·12 = 0, 3·8 = 0, 4·6 = 0, 9·8 = 0, etc.

Let R be a ring with identity and let a ∈ R. A multiplicative inverse of a is an element a^-1∈ R such that a·a^-1 = a^-1·a = 1. An element which has a multiplicative inverse is called a unit, e.g., the units in ℤ_n are the elements of U(n), that is, the elements of ℤ_n which are relatively prime to n. In ℤ₁₂, 1, 5, 7, and 11 are units. In ℤ₂₄: [24 = 2³·3] 1, 5, 7, 11, 13, 17, 19, 23, e.g., 5^-1 = 5, 7^-1 = 7, 11^-1 = 11.

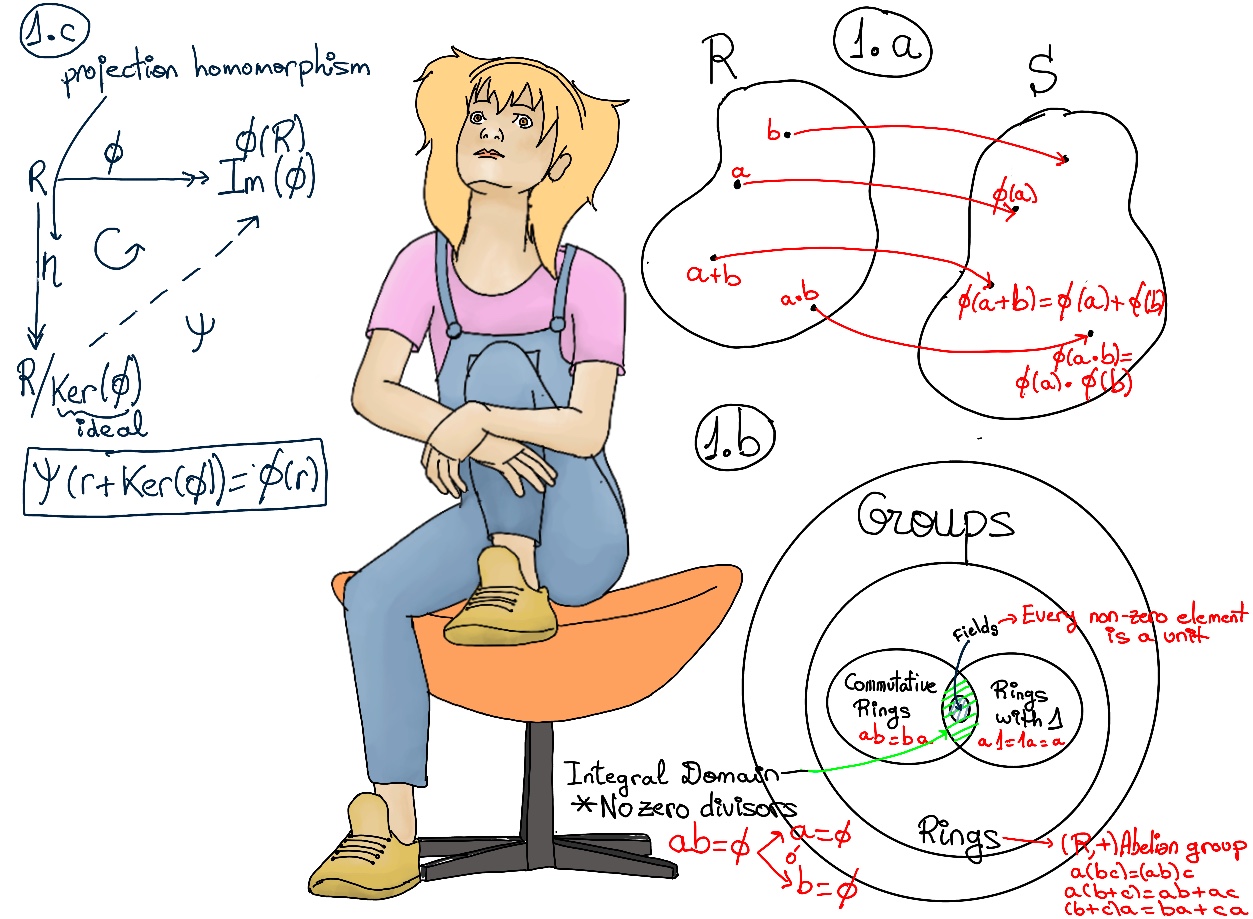
A field is a commutative ring with unity in which every non-zero element is a unit. Examples: ℤ/nℤ with n prime, ℝ, ℂ, ℚ, but not ℤ because in general, n ∈ ℤ ⇏ 1/n ∈ ℤ. Figure 1.b.  

Example

Let’s prove that R = {$1 = (\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}), a = (\begin{smallmatrix}1 & 1\\ 1 & 0\end{smallmatrix}), b = (\begin{smallmatrix}0 & 1\\ 1 & 1\end{smallmatrix}), 0 = (\begin{smallmatrix}0 & 0\\ 0 & 0\end{smallmatrix})$} with entries in ℤ₂ is a field.

(R, +, ·) is closed under both operations, commutative, and every non-zero element has a multiplicative inverse. Associativity and distributivity are inherited from the fact that we are inside M_nxn(ℤ₂), the ring of matrices under the usual matrix addition and multiplication. Therefore, it is a finite field, and char(R) = 2 (∀a, a + a = 0)

Definition. An integral domain is a commutative ring with unity and no zero-divisors.Thus, a product of two elements a, b ∈ R is 0 (ab = 0) only when one of the factor is 0 (a = 0 ó b = 0).

Let’s solve the equation x² + x -6 = 0 in ℤ₁₂. The left side of this equation can be factor as (x-2)(x+3) = 0, so the solutions are 2 (x -2 = 0) and -3 (x -3 = 0). There is a big assumption that we are taken for granted: if the product of two terms is zero then common sense 🐒 says at least one of the two terms has to be zero to start with.

However, this is not always the case, e.g., x² +5x + 6 ≡ 0 (mod 12) ↭ (x +2)(x + 3) ≡ 0 (mod 12). Consider the following facts,

1. x + 2 ≡ 0 (mod 12) ⇒ x ≡ 10 (mod 12).
2. x + 3 ≡ 0 (mod 12) ⇒ x ≡ 9 (mod 12).
3. We can see that this solution has not two, but four solutions: 1, 6, 9 and 10, that’s because 3·4 ≡ 0 (mod 12) even though 3 ≇ 0 (mod 12) and 4 ≇ 0 (mod 12). In other words, ℤ₁₂ has zero divisors.

The reason why an integral domain is required to be a commutative ring with no zero divisors is to be able to use the cancellation property, a·x = a·y (a ≠ 0) ⇒[(R, +) Abelian group] a·x -a·y = 0 ⇒[Distributive] a(x -y) = 0 ⇒[No zero divisors, a ≠ 0] x -y = 0 ⇒ x = y.

Examples

• Some integral domains are: ℤ, ℚ, ℝ, ℂ
• The Gaussian integers, ℤ[i] = {a + bi | a, b ∈ ℤ}, and the ring ℤ[x] of polynomial with integer coefficients are integral domains.

ℤ[i] is a subring of the complex numbers, ℂ, and hence it inherits all necessarily requirements. For completeness’ sake, let’s prove that there are no zero divisors.

∀z, w ∈ ℤ[i], such that w ≠ 0 and zw = 0, the question is z = 0?

z = a + bi, w = c + di, a, b, c, d ∈ ℤ, and by assumption, w ≠ 0 ⇒ c² + d² = 0

0 = zw = (a + bi)(c + di) = (ac -bd) + (ad +bc)i ⇒ ac -bd = 0 (i) and ad + bc = 0 (ii) ⇒[(ii)*c - (i)*d] adc + bc² - acd +bd² = bc² + bd² = b(c²+d²) ⇒[ℤ is an integral domain (no funny business, that is, no zero divisors), c² + d² = 0] b = 0 ⇒[b = 0 applied to i and ii] ac = ad = 0 ⇒ [ℤ is an integral domain (no funny business 🐒, that is, no zero divisors), c and d cannot be simultaneously zero] a = 0 ⇒[Recall we have shown that b = 0, too] z = 0∎

• ℤ[$\sqrt{2}$] = {a + b$\sqrt{2}$ | a, b ∈ ℤ } is a subring of ℝ and an integral domain, too.
• ℤ_p with p prime.
• Counterexample. ℤ_n, n composite is not an integral domain, e.g., ℤ₄, 2 + 2 = 0, so 2 is a zero divisor.
• Counterexample. The ring M₂(ℤ) of 2 x 2 matrices over the integers is not an integral domain either, because it has nonzero divisors, e.g., $(\begin{smallmatrix}1 & 1\\ 2 & 2\end{smallmatrix})(\begin{smallmatrix}1 & 1\\ -1 & -1\end{smallmatrix})=(\begin{smallmatrix}0 & 0\\ 0 & 0\end{smallmatrix})$
• Counterexample. ℤ x ℤ is not an integral domain, (0, 1)(1, 0) = (0, 0).
• Counterexample. 2ℤ is not an integral domain because 1 ∉ 2ℤ.

Properties

In rings, left and right cancellation laws generally do not hold.

Cancellation law. Let a, b, c ∈ R, let R be an integral domain. If a ≠ 0 and ab = ac ⇒ b = c.

Proof. If a ≠ 0 and ab = ac ⇒ ab - ac = 0 ⇒[Distributivity] a(b - c) = 0 ⇒ [a ≠ 0, R is an integral domain, so there are no zero divisors] b - c = 0 ⇒ b = c ∎

Proposition. Every field is an integral domain.

Proof.

Since a field is a commutative division (every nonzero element has a multiplicative inverse) ring, therefore, in order to show that every field is an integral domain we only need to prove that a field does not have zero divisors.

a, b ∈ R, a ≠ 0, ab = 0 ⇒ [a ∈ R, a ≠ 0, R field, ∃a^-1∈ R: aa^-1 = a^-1a = 1] a^-1ab = a^-1(ab) = a^-1·0 = 0 ⇒[a^-1ab = (a^-1a)b = b] b = 0 ∎

Proposition. Every finite integral domain is a field.

Let D be a finite integral domain, let 1 be its unit.

is D a field? ∀a ∈ D, a ≠ 0, is “a” an unit? ↭ does it have a multiplicative inverse? There are two possibilities:

1. a = 1, then a is its own inverse, and in particular is a unit.
2. Let a ≠ 1. Consider the following set, A = {a⁰ = 1, a, a², a³,…} ⊆ D ⇒ [D is finite] ∃i, j ∈ ℤ, i > j: aⁱ = a^j ⇒ [By cancellation law, let R be an integral domain. If a ≠ 0 and ab = ac ⇒ b = c.] a^i-j = 1 ⇒ i-j-1 ≥ 0, a^i-j-1 ∈ R and it is the inverse of a.

Examples

• $\mathbb{F_p}$ = ℤ/pℤ with p prime is a field. ℤ/ℤn is a field if and only if n is prime.

Proof. We already know that finite integral domains are fields. ℤp is obviously finite. Does it have no zero-divisors?

a, b ∈ ℤp, ab = 0, a = 0 ó b = 0?

ab =_ℤp 0 ⇒ ∃k: ab = pk ⇒ [Euclid’s Lemmma. p prime, p | ab ⇒ p | a or p | b. p | a or p | b, that is, a = 0 ó b = 0

• Z₃[i] = {a + bi | a, b ∈ ℤ₃} = {0, 1, 2, i, 1 + i, 2 + i, 2i, 2 + 2i, 2 + 2i} where i² = -1 =_ℤ3 2. It is the ring of Gaussian integers modulo 3 and a field. Addition and multiplication operate as in the complex numbers, but coefficients are reduced modulo 3, e.g., 2(2 + 2i) = 1 + i, 2i(1 + i) = 2i + 2i²=[-2 = 1] 2i -2 = 2i + 1.

Let’s check multiplicative inverses directly: 1·1 = 1, 2·2 = 1 (2 = 2^-1), (2i)i =2i² =1, (2+i)(1+i) = 2 + i² +3i = 2 -1 + 3i = 1, (1+2i)(2+2i) = 2 +i² + 6i = 2 -1 = 1.

• ℤ₂(α) = {a + bα| a, b ∈ ℤ₂, α² = α + 1} is also a finite field with four elements.

Let’s check multiplicative inverses directly: 1·1 = 1, α(α+1) = α² + α = 2α + 1 = 1, and there are no zero-divisors.

• ℚ[$\sqrt{2}$] = {a + b$\sqrt{2}$ | a, b ∈ ℚ} is not only a ring, but a field.

Let a + b$\sqrt{2}$, a, b ∈ ℚ. Let’s show that 1/(a+b$\sqrt{2}$) can be written as c + d$\sqrt{2}$, c, d ∈ ℚ:

$\frac{1}{a+b\sqrt{2}} = \frac{1}{a+b\sqrt{2}}\frac{a-b\sqrt{2}}{a-b\sqrt{2}} = \frac{a-b\sqrt{2}}{a^{2}-2b^{2}}=\frac{a}{a^{2}-2b^{2}}-\frac{b}{a^{2}-2b^{2}}\sqrt{2}$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.