Arc lengths

Just because something isn’t a lie does not mean that it isn’t deceptive. A liar knows that he is a liar, but one who speaks mere portions of truth in order to deceive is a craftsman of destruction, Criss Jami.

Recall

Antiderivatives are fundamental concepts in calculus. They are the inverse operation of derivatives.

Given a function f(x), an antiderivative, also known as indefinite integral, F, is the function that can be differentiated to obtain the original function, that is, F’ = f, e.g., 3x² -1 is the antiderivative of x³ -x +7 because $\frac{d}{dx} (x^3-x+7) = 3x^2 -1$. Symbolically, we write F(x) = $\int f(x)dx$.

The process of finding antiderivatives is called integration.

The Fundamental Theorem of Calculus states roughly that the integral of a function f over an interval is equal to the change of any antiderivate F (F'(x) = f(x)) between the ends of the interval, i.e., $\int_{a}^{b} f(x)dx = F(b)-F(a)=F(x) \bigg|_{a}^{b}$

Arc lengths

In calculus, the concept of arc length refers to the length of a curve in a two-dimensional plane. The integral represents the sum of all the infinitesimally small line segments along the curve, and the square root term ensures that the Pythagorean theorem is applied to these segments, that is, (Δs)² ≈ (Δx)² + (Δy)², and then, in the infinitesimal scale, (ds)² = (dx)² + (dy)² ⇒ ds = $\sqrt{dx^2+dy^2} = \sqrt{dx^2(1+(\frac{dy}{dx})^2)} = dx\sqrt{1+(\frac{dy}{dx})^2}$ (Figure 2.a.).

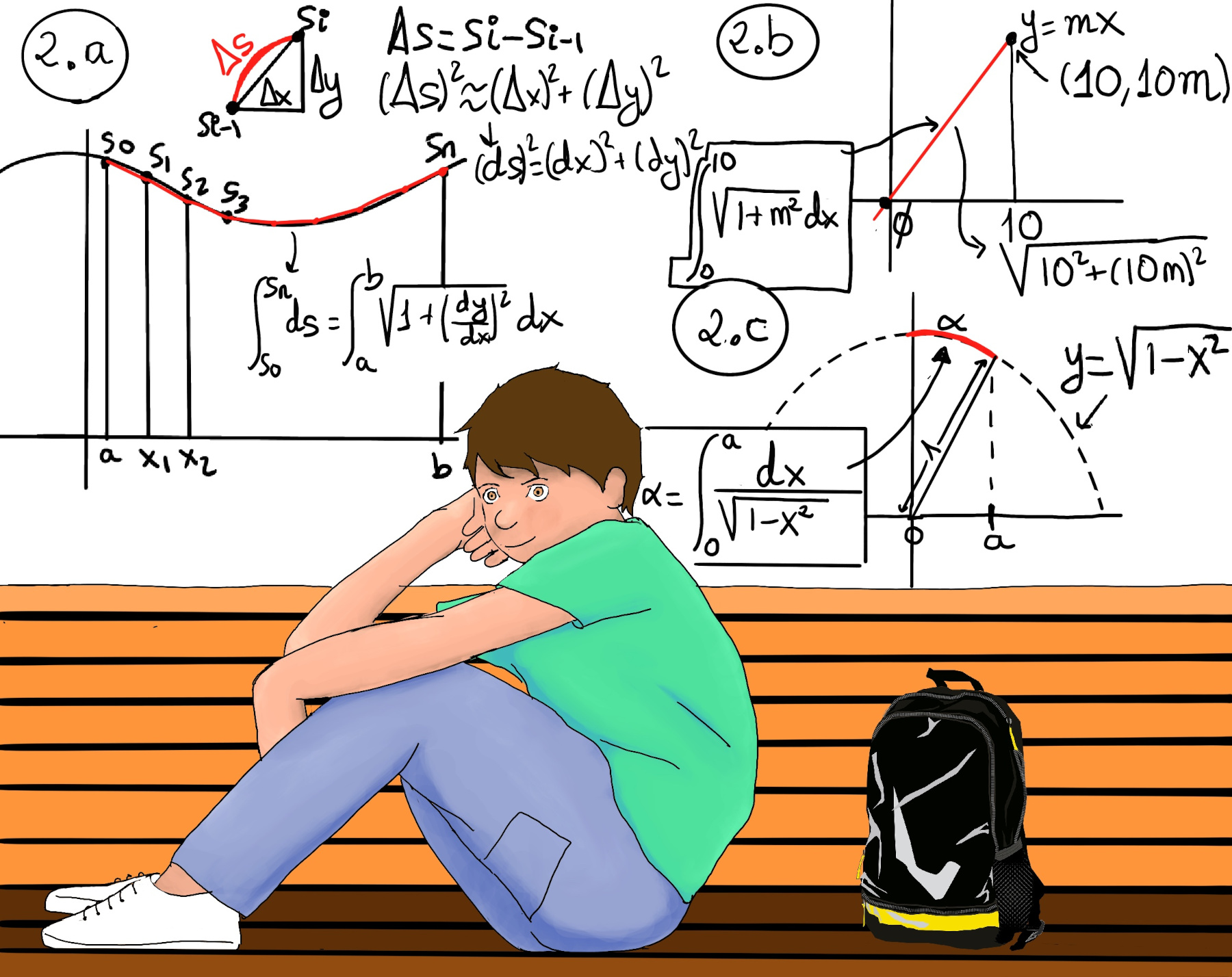
Hence, our length is $\int_{s_0}^{s_n} ds = \int_{a}^{b} \sqrt{1+(\frac{dy}{dx})^2}dx = \int_{a}^{b} \sqrt{1+f’(x)^2}dx$ where y = f(x). Let f be differentiable on [a, b], where f' is also continuous on [a, b]. Then, the arc length of f from x = a to x = b is$L = \int_{a}^{b} \sqrt{1+f'(x)^2}dx.$

Solved exercises

• Let’s suppose y = mx, y’ = dy/dx = m, ds = $\sqrt{1+(y’)^2}dx = \sqrt{1+m^2}dx$, the length between 0 and 10 is $\int_{0}^{10} \sqrt{1+m^2}dx = 10\sqrt{1+m^2}dx$ (Figure 2.b.)

• Determine the length of f(x) = $1+6x^{\frac{3}{2}}$ between 0 and 1.

ds = $\sqrt{1+(y’)^2}dx = \sqrt{1+(6·\frac{3}{2}·x^{\frac{3}{2}-1})^2}dx = \sqrt{1+81\sqrt{x}^2} = \sqrt{1+81x}$

The arc length is $\int_{0}^{1} \sqrt{1+81x}dx$= [U-substitution, u = 1+81x, du = 81dx, x = 0 ⇒ u = 1, x = 1 ⇒ u = 82] $\frac{1}{81}\int_{1}^{82} \sqrt{u}du = \frac{1}{81}·\frac{2}{3}u^{\frac{3}{2}} = \frac{2}{243}u^{\frac{3}{2}}\bigg|_{1}^{82} = \frac{2}{243}(82^{\frac{3}{2}}-1)≈ 6.1$

• Let’s assume y = $\sqrt{1-x^2}$ and calculate the arc length along the unit circle (Figure 2.c.), y’ = $\frac{-x}{\sqrt{1-x^2}}$, and the more complicated calculations implies ds = $\sqrt{1+(y’)^2}dx =$ [1+(y’)² = $1+(\frac{-x}{\sqrt{1-x^2}})^2 = 1 + \frac{x^2}{1-x^2} = \frac{1-x^2+x^2}{1-x^2} = \frac{1}{1-x^2}$] $\frac{dx}{\sqrt{1-x^2}}$.

The arc length is α = $\int_{0}^{a} \frac{dx}{\sqrt{1-x^2}}$ =[x = sin(θ), dx = cos(θ)dθ, x = 0 ⇒ θ = 0, x = a ⇒ a = sin(θ) ⇒ θ = sin^-1(a)] $ = \int_{0}^{sin^{-1}a} \frac{cos(θ)dθ}{\sqrt{1-sin^2(θ)}} = \int_{0}^{sin^{-1}a} \frac{cos(θ)dθ}{cos(θ)} = \int_{0}^{sin^{-1}a} dθ = θ\bigg|_{0}^{sin^{-1}a} = sin^{-1}a$ ↭ a = sin(α). Therefore, the integral evaluates to $\arcsin(a)$, which represents the arc length of the upper half of the unit circle from 0 to a.

• Determine the length of x = $\frac{2}{3}(y-1)^{\frac{3}{2}}$ between 1 and 4 (1 ≤ y ≤ 4).

ds = $\sqrt{1+(x’)^2}dy = \sqrt{1+(\frac{2}{3}·\frac{3}{2}·\sqrt{y-1})^2}dy = \sqrt{1+y-1}=\sqrt{y}$

Hence, the length between 1 and 4 is $\int_{1}^{4} \sqrt{y}dy = \frac{2}{3}y^{\frac{3}{2}}\bigg|_{1}^{4} = \frac{2}{3}(4^{\frac{3}{2}}-1) = \frac{2}{3}(8-1) = \frac{14}{3}$.

• Find the surface area of the solid formed by revolving the curve y = x² on [0, 1] about the x-axis and the y-axis.

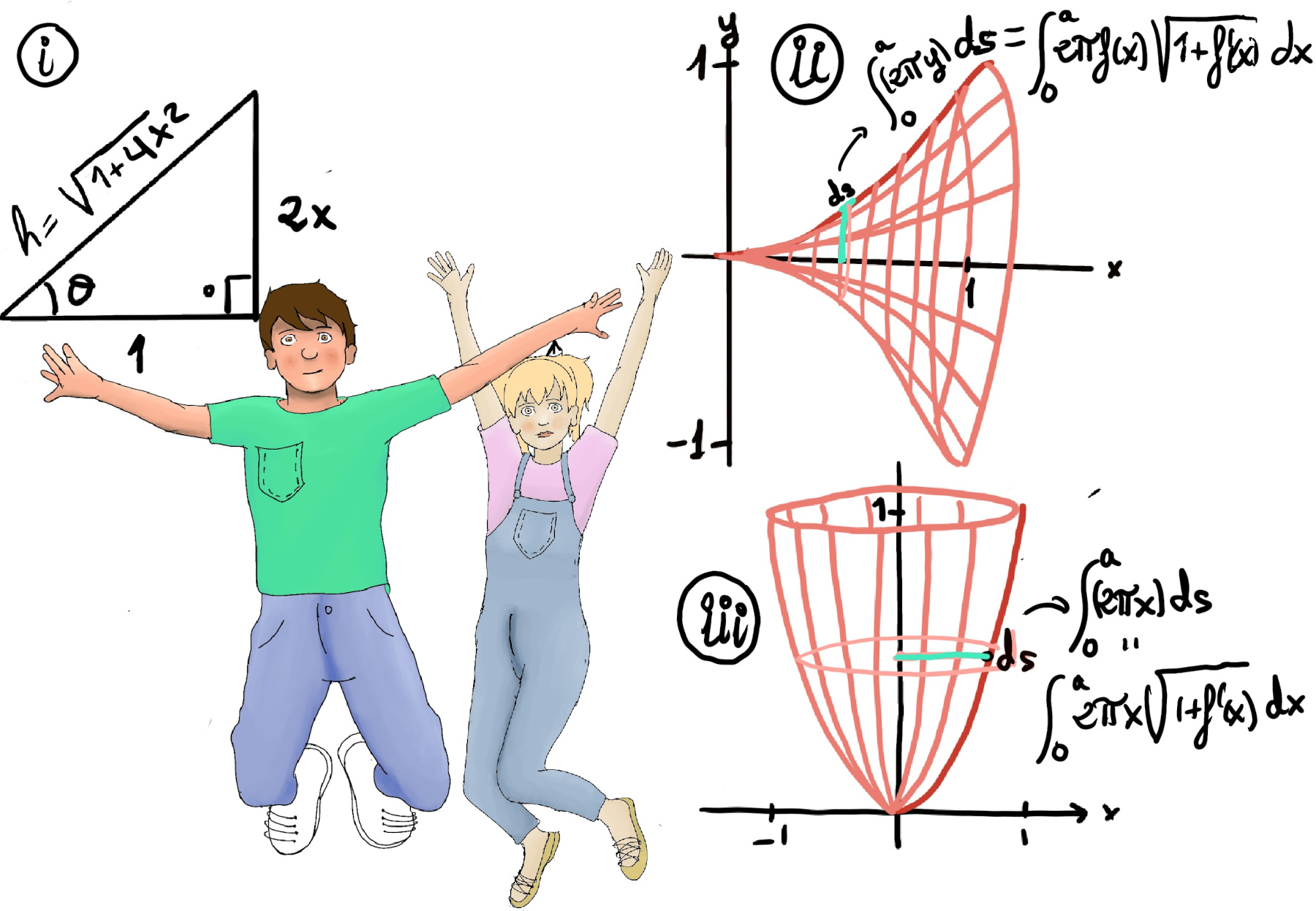
About the x-axis, it is relatively easy to set up, y’ = 2x, ds = $\sqrt{1+(2x)^2}dx$ (Figure 2.d. and ii).

The arc length (0 ≤ x ≤ 1) is $\int_{0}^{1} \sqrt{1+4x^2}dx$.

Let’s calculate its surface area (this is a measure of the total area that the surface of the object occupies) of the parabola y = x² rotated around the x-axis, dA = (2πy)ds, hence its surface area = $\int_{0}^{1} (2πy)ds = \int_{0}^{1} (2πx^2)\sqrt{1+4x^2}dx = 2π\int_{0}^{1} x^2\sqrt{1+4x^2}dx$[Trigonometric substitution, it’s not for the faint of heart 😃, tan(θ) = 2x, Figure i, $tan(θ) = \frac{2x}{1}, sec(θ)=\frac{\sqrt{1+4x^2}}{1} = \sqrt{1+4x^2}$, tan(θ)=2x ⇒ $sec^2(θ)dθ = 2dx ⇒ dx = \frac{sec^2(θ)dθ}{2}$] $2π\int_{0}^{1} \frac{tan^2(θ)}{4}sec(θ)\frac{sec^2(θ)dθ}{2} = \frac{π}{4}\int_{0}^{1} tan^2(θ)sec^3(θ)dθ$ =[Pythagorean identities, 1 +tan²(θ) = sec²(θ)] $\frac{π}{4}\int_{0}^{1} (sec^2(θ)-1)sec^3(θ)dθ = \frac{π}{4}\int_{0}^{a} (sec^5(θ)-sec^3(θ))dθ$ =[🚀]

$\int sec^3(x)dx = \int sec^2(x)sec(x)dx$ [Integration by parts, u = sec(x), v’ = sec²(x)dx, du = sec(x)tan(x)dx, v = tan(x)] $sec(x)tan(x) -\int tan(x)sec(x)tan(x)dx = sec(x)tan(x) -\int tan^2(x)sec(x)dx = sec(x)tan(x) -\int (sec^2(x)-1)sec(x)dx = sec(x)tan(x) -\int (sec^3(x)-sec(x))dx ⇒ \int sec^3(x)dx = sec(x)tan(x) -\int sec^3(x)dx +\int sec(x)dx ⇒ \int sec^3(x)dx = \frac{1}{2}(sec(x)tan(x)+\int sec(x)dx) = \frac{1}{2}(sec(x)tan(x)+ln|sec(x)+tan(x)|) + C$

$\int sec^5(x)dx = \int sec^3(x)sec^2(x)dx$ [Integration by parts, u = sec³(x), v’ = sec²(x)dx, v = tan(x), u’=3sec²(x)sec(x)tan(x) = 3tan(x)sec³(x)] = $sec^3(x)tan(x) -\int tan(x)·3tan(x)sec^3(x)dx = sec^3(x)tan(x) -3\int tan^2(x)sec^3(x)dx =$[1+tan²(x) = sec²(x)] $sec^3(x)tan(x) -3\int (sec^2(x)-1)sec^3(x)dx = sec^3(x)tan(x) -3\int sec^5(x)dx +3\int sec^3(x)dx ⇒ \int sec^5(x)dx = sec^3(x)tan(x) -3\int sec^5(x)dx +3\int sec^3(x)dx ⇒ \int sec^5(x) = \frac{1}{4}(sec^3(x)tan(x) +3\int sec^3(x)dx) = \frac{1}{4}(sec^3(x)tan(x) + \frac{3}{8}(sec(x)tan(x)+ln|sec(x)+tan(x)|))+C$

Back to our original integral [🚀], $\frac{π}{4}\int_{0}^{1} (sec^2(θ)-1)sec^3(θ)dθ = \frac{π}{4}\int_{0}^{1} (sec^5(θ)-sec^3(θ))dθ$ =[🚀] $\frac{π}{4} ( \frac{1}{4}(sec^3(θ)tan(θ) + \frac{3}{8}(sec(θ)tan(θ)+ln|sec(θ)+tan(θ)|)) - (\frac{1}{2}(sec(θ)tan(θ)+ln|sec(θ)+tan(θ)|) )\bigg|_{0}^{1}$, but we are by no means done, we need to backtrack substitutions, so consider that tan(θ) = 2x, θ = tan^-1(2x), and so on… (It is left to the reader as a “very easy and short” exercise…😄)

We can obviously generalize this result. Let f(x) be a nonnegative continuous function over the interval [a,b]. Then, the surface area of the surface of revolution formed by revolving the graph of y = f(x) around the x-axis is given by $\int_{a}^{b} 2πy\sqrt{1+(f'(x)^2)}dx = \int_{a}^{b} 2πf(x)\sqrt{1+(f'(x)^2)}dx.$

About the y-axis (Figure iii), since we are revolving about the y-axis, the radius of the solid is not f(x), but rather x, so the surface area is $2π \int_{0}^{1} x\sqrt{1+(2x)^2}dx =$[u = 1 +4x², du = 8xdx, x = 0 ⇒ u = 1, x = 1 ⇒ u = 5] $\frac{π}{4} \int_{1}^{5} \sqrt{u}du =\frac{π}{4}·\frac{2}{3}u^{\frac{3}{2}}\bigg|_{1}^{5}du = \frac{π}{6}(5\sqrt{5}-1)≈5.33$

As we did before, the surface area of revolution formed by revolving the graph of y = f(x) around the y-axis is given by $\int_{a}^{b} 2πx\sqrt{1+(f'(x)^2)}dx.$

• Surface area of the surface generated by revolving $f(x)=\sqrt{x}$ over the interval [1, 4] around the x-axis.

f’(x) = $\frac{1}{2\sqrt{x}}$

Surface Area = $\int_{a}^{b} 2πf(x)\sqrt{1+(f’(x)^2)}dx = \int_{1}^{4} 2π\sqrt{x}\sqrt{1+\frac{1}{4x}}dx = 2π\int_{1}^{4} \sqrt{x+\frac{1}{4}}dx =$[u = x + ¹⁄₄, du = dx, x = 1 ⇒ u = ⁵⁄₄, x = 4 ⇒ u = ¹⁷⁄₄] $2π\int_{\frac{5}{4}}^{\frac{17}{4}} \sqrt{u}du = 2π\frac{2}{3}u^{\frac{3}{2}}=\frac{4π}{3}u^{\frac{3}{2}}\bigg|_{\frac{5}{4}}^{\frac{17}{4}}≈30.846$

• Surface area of a sphere with radius a. y = $\sqrt{a^2-x^2}, y’=\frac{-x}{\sqrt{a^2-x^2}}, 1 + (y’)^2 = 1 + \frac{x^2}{a^2-x^2} = \frac{a^2-x^2+x^2 }{a^2-x^2} = \frac{a^2}{a^2-x^2}$ (Figure 2.e.)

Surface Area = $\int_{x_1}^{x_2} 2πyds = \int_{x_1}^{x_2} 2π\sqrt{a^2-x^2}\sqrt{\frac{a^2}{a^2-x^2}}dx = \int_{x_1}^{x_2} 2πadx = 2πa(x_2-x_1)$, e.g., the hemisphere x₁ = 0, x₂ = a, area = 2πa(a) = 2πa²; and the whole sphere, x₁ = -a, x₂ = a, area = 2πa(a -(-a)) = 4πa².

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.