Prime and Maximal ideals

“There was a street evangelist who was trying to get the attention of passersby, he was urging them to flee from the wrath to come -I warn you, there will be weeping, wailing, and gnashing of teeth! An old woman in the crowd replied, -Sir, I do not have teeth! And the evangelist retorted, -Lady, teeth will be provided!” Apocalypse, Anawim, #justtothepoint.

Recall

💍 A ring R is a non-empty set with two binary operations, addition (a + b) and multiplication (ab), such that ∀ a, b, c ∈ R:

1. Both operations are closed: a + b ∈ R, a·b ∈ R.
2. Commutative under addition: a + b = b + a.
3. Associative under addition: (a + b) + c = a + (b + c).
4. There is an additive identity 0 ∈ R such that a + 0 = a, ∀ a ∈ R.
5. There are inverse elements for addition, ∃-a ∈ R: a + (-a) = (-a) + a = 0.
6. Associative under product: a(bc) = (ab)c.
7. Multiplication is distributive over addition: a(bc) = ab + ac, (b + c)a = ba + ca.

A subring A of a ring R is called a (two-sided) ideal of R if it absorbs multiplication from the left and right from R, that is, ∀r ∈ R, a ∈ A, ra ∈ A and ar ∈ A. In other words, ∀r ∈ R, rA = {ra | a ∈ A} ⊆ A and Ar = {ar | a ∈ A} ⊆ A.

Let A ⊂ R, A ≠ R, R be a ring, A is an ideal of R if the following conditions are satisfied:

1. a - b ∈ A, ∀a, b ∈ A.
2. ∀r ∈ R, ∀a ∈ A, ra ∈ A and ar ∈ A.

Let R be a ring and let I be an ideal of R. In particular, R is an Abelian group under addition, and I is a normal subgroup of R, I ◁ R, therefore we could form the factor group R/I = {r + I | r ∈ R}.

Theorem. Let R be a ring and let I be a subring of R. The set of cosets R/I = {r + I | r ∈ R} is a ring under the operations (s + I) + (t + I) = (s + t) + I and (s + I)(t + I) = st + I iff I is an ideal of R.

More examples

• Consider the factor ring of the Gaussian integers R = ℤ[i]/⟨2 -i⟩.

The Gaussian integers are the set ℤ[i] = {x + iy : x, y ∈ ℤ} of complex numbers whose real and imaginary parts are both integers.

ℤ[i] is a ring (it is indeed a subring of ℂ) since it is closed under addition and multiplication: (x + iy) + (p + iq) = (x + p) + i(y + q), (x + iy)(p + iq) =[i² = -1] (xp − yq) + i(xq + yp).

2 -i + ⟨2 -i⟩ =[aH = H ↭ a ∈ H = 0 + H] 0 + ⟨2 -i⟩, so when dealing with coset representatives 2 -i ≡ 0 or 2 = i, e.g., 5 + 6i + ⟨2 -i⟩ = 5 + 6·2 + ⟨2 -i⟩ = 17 + ⟨2 -i⟩. In other words, ∀r ∈ R, r = a + ⟨2 -i⟩, a ∈ ℤ. Futhermore, 2 = i ⇒ 4 = i² = -1 or 5 = 0.

5 + 6i + ⟨2 -i⟩ = 17 + ⟨2 -i⟩ = 2 + 5 + 5 + 5 + ⟨2 -i⟩ = 2 + ⟨2 -i⟩. It follows that ℤ[i]/⟨2 -i⟩ is likely to be {0 + ⟨2 -i⟩ = ⟨2 -i⟩, 1 + ⟨2 -i⟩, 2 + ⟨2 -i⟩, 3 + ⟨2 -i⟩, 4 + ⟨2 -i⟩}.

Are these five cosets distinct? 5(1 + ⟨2 -i⟩) =[(a + I) + (b + I) = (a + b) + I] 5 + ⟨2 -i⟩ = 0 + ⟨2 -i⟩. So 1 + ⟨2 -i⟩ has order 5 or 1.

Let’s suppose for the sake of contradiction 1 + ⟨2 -i⟩ has order 1, i.e., 1 + ⟨2 -i⟩ = 0 + ⟨2 -i⟩ ⇒ 1 ∈ ⟨2 -i⟩ ⇒ ∃a + bi ∈ ℤ[i] such that 1 = (2 - i)(a + bi) = 2a + b + (-a + 2b)i ⇒ 1 = 2a + b, 0 = -a + 2b ⇒ a = 2/5, b =1/5 ⊥ Hence, ℤ[i]/⟨2 -i⟩ = {0 + ⟨2 -i⟩ = ⟨2 -i⟩, 1 + ⟨2 -i⟩, 2 + ⟨2 -i⟩, 3 + ⟨2 -i⟩, 4 + ⟨2 -i⟩} ≋[|ℤ[i]/⟨2 -i⟩| = 5, 5 is prime] ℤ₅.

• Let R = {f: ℝ → ℝ| f is a continuous function}, I = {f ∈ ℝ | f(0) = f(1) = 0}.

1. Subring. ∀f, g ∈ I, f(0) = f(1) = 0 and g(0) = g(1) = 0 ⇒ (f - g)(0) = f(0) - g(0) = (f - g)(1) = f(1) - g(1) = 0 ⇒ f - g ∈ I. (f · g)(0) = f(0) · g(0) = (f · g)(1) = f(1) · g(1) = 0 ⇒ f · g ∈ I.
2. Absorption. ∀f ∈ I, h ∈ R, f(0) = f(1) = 0 ⇒ (f·h)(0) = f(0)·h(0) = 0, (f·h)(1) = f(1)·h(1) = 0 ⇒ f·h ∈ I.

• Let ℝ[x] be the ring of polynomials with real coefficient, let ⟨x² + 1⟩ be the principal ideal generated by x² + 1.

⟨x² + 1⟩ = {f(x)(x² + 1) | f(x) ∈ ℝ[x]}.

ℝ[x]/⟨x² + 1⟩ = {g(x) + ⟨x² + 1⟩ | g(x) ∈ ℝ[x]}. Let g(x) ∈ ℝ[x] ⇒ [By dividing g(x) by x² + 1] g(x) = q(x)(x² + 1) + r(x) where q(x) is the quotient, r(x) is the remainder, degree of r(x) < 2 ⇒ r(x) = ax + b, a, b ∈ ℝ.

g(x) + ⟨x² + 1⟩ = q(x)(x² + 1) + r(x) + ⟨x² + 1⟩ = r(x) + ⟨x² + 1⟩ where r(x) = ax + b, a, b ∈ ℝ because the ideal ⟨x² + 1⟩ absorbs the term q(x)(x² + 1). Therefore, ℝ[x]/⟨x² + 1⟩ = {g(x) + ⟨x² + 1⟩ | g(x) ∈ ℝ[x]} = {ax + b + ⟨x² + 1⟩ | a, b ∈ ℝ} where x² + ⟨x² + 1⟩ = -1 + ⟨x² + 1⟩.

Observe that x² + 1 + ⟨x² + 1⟩ = 0 + ⟨x² + 1⟩, and so when dealing with coset representatives x² + 1 = 0 or x² = -1. Example: (x + 7 + ⟨x² + 1⟩)·(3x + 4 + ⟨x² + 1⟩) = 3x² + 25x + 28 + ⟨x² + 1⟩ =[28 -3] 25x + 25 + ⟨x² + 1⟩. The quotient ring R[X] / ⟨X² + 1⟩ is naturally isomorphic to the field of complex numbers ℂ, with the class [X] playing the role of the imaginary unit i.

The evaluation map Φ: ℝ[x] → ℂ, f(x)→ f(i) is onto, Ker(Φ) = ⟨x² +1⟩ ⇒By the first isomorphism theorem, ℝ[x]/⟨x²+1⟩ ≋ ℂ.

Prime and Maximal ideals

A prime ideal A of a commutative ring R is a proper ideal of R such that if a, b are two elements of R, and whenever their product ab is an element of A, then either a is in A, b is in A or both, i.e., a, b ∈ R, ab ∈ A ⇒ a ∈ A or b ∈ A. Example: ⟨x⟩ ⊆ ℤ[x] is a prime ideal, but ⟨x²⟩ is not, because x² ∈ ⟨x²⟩ but x ∉ ⟨x²⟩.

This generalizes Euclid’s lemma: if p is a prime number and if p divides a product ab of two integers, then p divides a or p divides b. We have basically exchanged or abstracted divisibility with being an element of an ideal.

A maximal ideal A of a commutative ring R is a proper ideal of R that is maximal with respect to set inclusion amongst all proper ideals, i.e., whenever B is an ideal of R that lives between R and A, A ⊆ B ⊆ R, then B = A or B = R. In other words, we cannot fit any proper ideals between the ring and a maximal ideal.

Examples:

• The prime ideals of ℤ are {0} and pℤ where p is prime.

Proof.

1. Suppose ab ∈ {0} ⇒ ab = 0 ⇒[ ℤ is an integral domain] a = 0 or b = 0 ⇒ a ∈ {0} or b ∈ {0}.
2. Suppose I ⊆ ℤ, I ≠ {0}, I is a prime ideal ⇒[Proposition. Every ideal of ℤ is a principal ideal.] I = nℤ = ⟨n⟩ = {···-2n, -n, 0, n, 2n, ···} for some n ∈ ℕ. A prime ideal is a proper ideal, so n is not allowed to be 1 (I = ⟨1⟩ ⇒ I = ℤ), n ≥ 2.
3. Let’s prove that n is prime. Let’s suppose a, b, such that 1 ≤ a, b ≤ n, ab = n ∈ I ⇒[I is prime] a ∈ I or b ∈ I. Without loss of generality, we could assume that a ∈ I ⇒ a ∈ nℤ = ⟨n⟩ = {···-2n, -n, 0, n, 2n, ···}, 1 ≤ a ≤ n ⇒ a = n ⇒ b = 1 ⇒ n is prime.

• In the ring of integers, the maximal ideals are the principal ideals generated by a prime number.
• ⟨2⟩ and ⟨3⟩ are maximal ideals for ℤ₃₆ and ℤ₂₄. ⟨2⟩, ⟨3⟩, and ⟨5⟩ are maximal ideals for ℤ₃₀. ⟨2⟩ is the maximal ideal for ℤ₈.

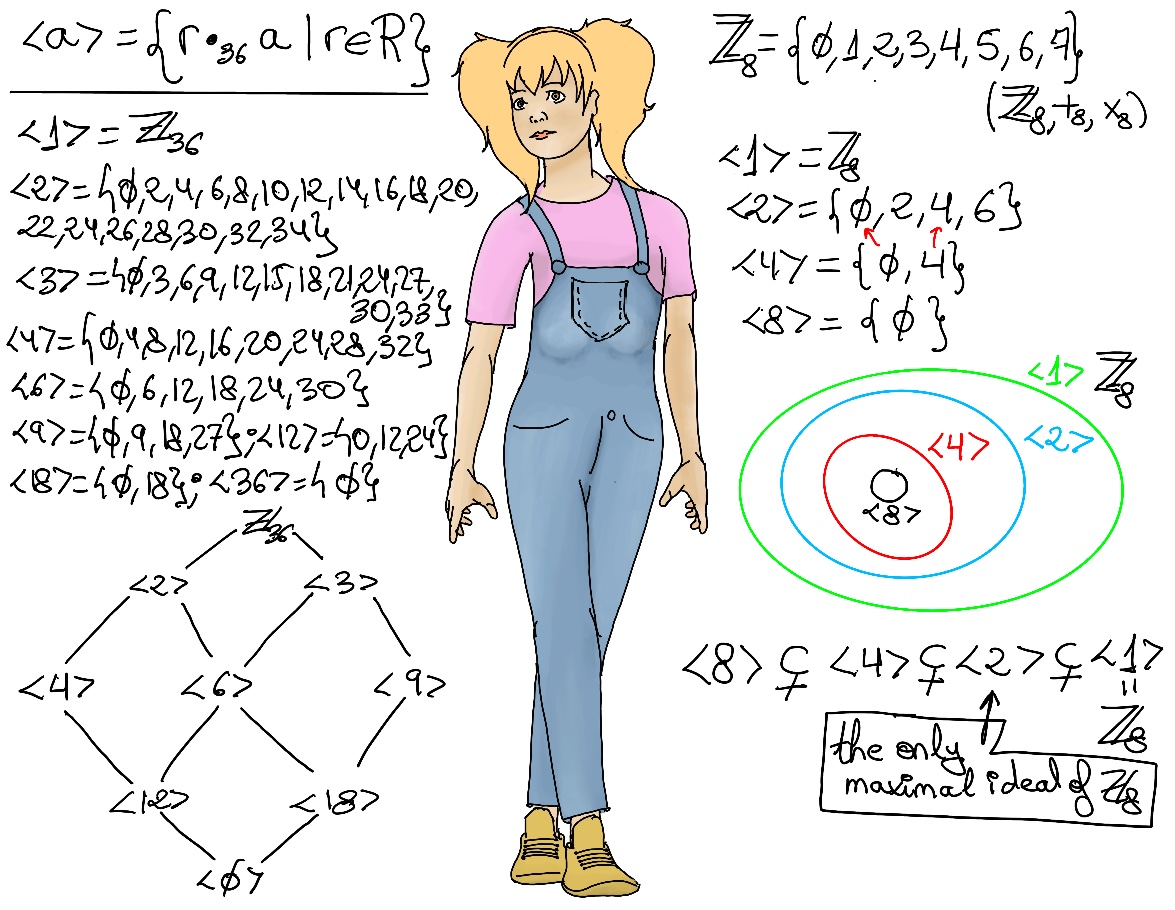
The ideals of ℤ_n are additive subgroups of ℤ_n, and we know that additive subgroups of ℤ_n have the form ⟨d⟩ where d divides n. Therefore, the ideals in ℤ_n are precisely the sets of the form ⟨d⟩ where d divides n.

⟨2⟩ = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34}
⟨3⟩ = {0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 36}

If gcd(k, 36) = 1, then ⟨k⟩ = ℤ₃₆, and observe that every integer not coprime with 36 is listed above, therefore ⟨2⟩ and ⟨3⟩ are our maximal ideals.    

• The ideal I = ⟨x² + 1⟩ is a maximal ideal in ℝ[x]. ⟨x² + 1⟩ denotes the principal ideal generated by x² + 1, i.e., ⟨x² + 1⟩ = {f(x)(x² + 1) | f(x) ∈ ℝ[x]} and ℝ[x] denotes the ring of polynomials with real coefficients.

Let A be an ideal of ℝ[x] that properly contains ⟨x² + 1⟩, i.e., I = ⟨x² + 1⟩ ⊂ A ⊆ ℝ[x] ⇒ ∃f(x) ∈ A, but f(x) ∉ ⟨x² + 1⟩ ⇒ f(x) = q(x)(x² + 1) + r(x), deg(r(x)) < 2, so r(x) = ax + b, where a and b are not both simultaneously equal to zero (a² + b² ≠ 0) because f(x) ∉ ⟨x² + 1⟩.

ax + b = r(x) = f(x) -q(x)(x² + 1) ∈ A ⇒ [By assumption, A is an ideal, (ax -b) ∈ ℝ[x]] a²x² -b² = (ax + b)(ax -b) ∈ A and [x² + 1 ∈ ⟨x²+1⟩ ⊆ A, a² ∈ ℝ[x]] a²(x² + 1) ∈ A ⇒ 0 ≠ a² + b² =[We have already demonstrated that a²(x² + 1) = (a²x² + a²) ∈ A and a²x² -b² ∈ A] (a²x² +a²) - (a²x² -b²) ∈ A, hence 0 ≠ a² + b² ∈ A.

Therefore, ∃c ∈ ℝ, c ≠ 0, c ∈ A ⇒ 1 = (1/c)c ∈ A ⇒ [∀f(x) ∈ ℝ[x], f(x) = 1f(x) ∈ A] A = ℝ[x] ∎

• The ideal I = ⟨x² + 1⟩ is not prime in ℤ₂[x], ⟨x² + 1⟩ = {f(x)(x² + 1) | f(x) ∈ ℤ₂[x]}, since it contains (x + 1)² = x² + 2x + 1 = x² + 1, but x + 1 ∉ ⟨x² + 1⟩. Alternatively, x² + 1 =[1 =_ℤ2 -1] x² - 1 = (x-1)(x+1), but neither x -1, nor x + 1 are in ⟨x² + 1⟩.

  Recall the definition of prime ideal in commutative rings, ab ∈ A ⇒ a ∈ A or b ∈ A

Theorem. Let R be a commutative ring with unity, and let A be an ideal of R. Then, A is a prime ideal iff R/A is an integral domain.

Proof.

⇐) Suppose that R/A is an integral domain. is A prime? ∀a, b ∈ R, such that ab ∈ A ⇒ a ∈ A or b ∈ A?

(a + A)(b + A) = ab + A = [ab ∈ A, aH = H ↭ a ∈ H] A, the zero element of the ring R/A. However, by assumption, R/A is an integral domain ⇒ it cannot have zero divisors ⇒ a + A or b + A is zero (R/A) ⇒ a + A = 0 + A = A ↭ a ∈ A or b + A = 0 + A = A ↭ b ∈ A

⇒) Suppose A is prime. What does it mean to be an integral domain? It means to be a commutative ring with multiplicative identity and no zero divisors. R/A is already a commutative ring with multiplicative identity for any proper ideal A. We claim that R/A has no zero-divisors.

Let’s suppose that there exist a + A, b + A, such that (a + A)(b + A) = 0 + A = A ⇒ ab ∈ A ⇒ [A is a prime ideal] a ∈ A or b ∈ A ⇒ a + A = A or b + A = A, i.e., a + A or b + A is the zero coset, i.e., the zero element in R/A ∎

Theorem. Let R be a commutative ring with unity and let A be an ideal of R. Then, R/A is a field iff A is a maximal ideal.

Proof

⇐) Suppose that A is a maximal ideal. We need to show that every non-zero element of R/A has a multiplicative inverse (all other properties follow quite trivially).

Let’s take a non-zero element of R/A, say b + A ∈ R/A, b ∉ A (Otherwise, if b ∈ A ⇒ b + A = A = 0 + A). Consider the following change of ideals, A ⊂ ⟨b⟩ + A ⊂ R ⇒[By assumption, A is a maximal ideal, and we also know that b ∉ A] ⟨b⟩ + A = R ⇒[By assumption, R is a commutative ring with unity] 1 ∈ ⟨b⟩ + A ⇒ 1 = br + a’ for some r ∈ R, a’ ∈ A ⇒[1 -br ∈ A, a + H = b + H ↭ a^-1b ∈ H] 1 + A = br + A ⇒ (b + A)(r + A) = br + A = 1 + A, and therefore we have just found the multiplicative inverse of b + A ∎

Recall Given a ring R with ideals I, J ⊆ R, I + J = {i + j | i ∈ I, j ∈ J}, IJ = {i₁j₁ + ··· + i_nj_n | i_k ∈ I, j_k ∈ J, ∀k: 1 ≤ k ≤ n} I ∩ J, I + J, IJ are all ideals. In particular, I + J is an ideal and ⟨b⟩ + A is an ideal.

⇒) Suppose R/A is a field. is A maximal?

Let B an ideal of R properly containing A, A ⊆ B, A ≠ B ⇒ ∃b ∈ B, b ∉ A ⇒ b + A is an non zero element of R/A ⇒ [R/A is a field, there are multiplicative inverses for all non zero elements] ∃c + A ∈ R/A such that 1 + A = (b + A)·(c + A) = bc + A ⇒ 1 - bc ∈ A ⊂ B ⇒ 1 - bc ∈ B ⇒[bc ∈ B because b ∈ B, c ∈ R] 1 - bc + bc ∈ B ⇒ 1 ∈ B ⇒ ∀r ∈ R, 1.r = r ∈ B ⇒ B = R ⇒[B is an arbitrary ideal of R containing A] A is maximal.

Corollary. Let R be a commutative ring with unity, let A be a maximal ideal ⇒ R/A is a field, and in particular R/A is an integral domain ⇒[Theorem. Let R be a commutative ring with unity, and let A be an ideal of R. Then, A is a prime ideal iff R/A is an integral domain] A is prime.

Examples

• Let ℤ[x] be the ring of polynomials with integer coefficients, let I = ⟨x⟩. If f(x) ∈ I, f(x) = x(a_nxⁿ+···+a₁x + a₀), it satisfies f(0) = 0. I = ⟨x⟩ = {f(x) ∈ ℤ[x] | f(0) = 0}. Conversely, {f(x) ∈ ℤ[x] | f(0) = 0} ⊆ ⟨x⟩ because f(x) = a_nxⁿ+···+a₁x = x(a_nx^n-1+···+a₁) ∈ ⟨x⟩

The ideal ⟨x⟩ = {f(x) ∈ ℤ[x]| f(0) = 0} ⊆ ℤ[x] is prime because ℤ[x]/⟨x⟩ ≋ ℤ is an integral domain [Recall, let R be a commutative ring with unity, and let A be an ideal of R. Then, A is a prime ideal iff R/A is an integral domain], but not maximal because ℤ is not a field [Recall. Let R be a commutative ring with unity and let A be an ideal of R. Then, R/A is a field iff A is a maximal ideal].

Let Φ: ℤ[x] → ℤ, Φ(f(x)) = f(0). Φ is clearly surjective. Ker(Φ) = ⟨x⟩ = {f(x) ∈ ℤ[x]| f(0) = 0}. By the First Isomorphism Theorem for rings, ℤ[x]/⟨x⟩ ≋ ℤ.

Another way of demonstrating ⟨x⟩ is prime is as follows, If g(x)h(x) ∈ ⟨x⟩ = {f(x) ∈ ℤ[x] | f(0) = 0}, then g(0)h(0) = 0 ⇒ [g(0), h(0) ∈ ℤ and ℤ is an integral domain -integral domains are generalizations of the ring of integers-] g(0)=0 or h(0) = 0 ⇒ g(x) ∈ ⟨x⟩ or h(x) ∈ ⟨x⟩. Therefore, ⟨x⟩ is a prime ideal in ℤ[x].

• ⟨x, 2⟩ is maximal ↭ ℤ[x]/⟨x, 2⟩ ≋ ℤ/2ℤ is a field.

⟨x⟩ is not maximal because ⟨x⟩ ⊂ ⟨x, 2⟩ ⊂ ℤ[x].

An element in ⟨x, 2⟩ has the form f(x) = xg(x) + 2h(x) ⇒ f(0) = 2h(0), so I = ⟨x, 2⟩ ⊆ {f(x)∈ℤ[x] | f(0) is an even integer}.

Let f(x) ∈ {f(x)∈ℤ[x] | f(0) is an even integer} ⇒ f(x) = a_nxⁿ+···+a₁x+ 2k =[Recall that the ideal generated by the family a₁, a₂, ···, a_n is ⟨a₁, a₂, ···, a_n⟩ = {r₁a₁ + r₂a₂ + ··· + r_na_n | r_i ∈ R}] x(a_nx^n-1+···+a₁) + 2k ∈ ⟨x, 2⟩, therefore {f(x)∈ℤ[x] | f(0) is an even integer} ⊆ I = ⟨x, 2⟩, hence I = ⟨x, 2⟩ = {f(x)∈ℤ[x] | f(0) is an even integer}.

ℤ[x]/⟨x, 2⟩ is a field because every element of ℤ[x]/⟨x, 2⟩ can be expressed as

1. a_nxⁿ+···+a₁x + 2k + ⟨x, 2⟩ = 0 + ⟨x, 2⟩
2. a_nxⁿ+···+a₁x + (2k + 1) + ⟨x, 2⟩ =[a_nxⁿ+···+a₁x + 2k is absorbed by ⟨x, 2⟩] 1 + ⟨x, 2⟩

Therefore, ℤ[x]/⟨x, 2⟩ ≋ ℤ₂ ⇒ ℤ[x]/⟨x, 2⟩ is a field ⇒ ⟨x, 2⟩ is both prime and maximal.

Another way of proving ℤ[x]/⟨x, 2⟩ ≋ ℤ₂ is as follows. Let Φ: ℤ[x] → ℤ, Φ(f(x)) = f(0), ψ: ℤ → ℤ₂, ψ(x) = x mod 2. Consider the composite homomorphism ψ ∘ Φ: ℤ[x] → ℤ₂. ψ ∘ Φ is obviously onto. Ker(ψ ∘ Φ) = {f(x)∈ℤ[x] | f(0) is an even integer} = ⟨x, 2⟩. By the First Isomorphism Theorem for Rings, ℤ[x]/⟨x, 2⟩ ≋ ℤ₂.

• Let Z[i] = {a + bi|a, b ∈ ℤ} be the Gaussian integers. I = ⟨3 -i⟩ ⊆ ℤ[i] is not a prime ideal. (1 + i)(1 - 2i) = (3 -i), but 1 + i ∉ ⟨3 -i⟩ and (1 -2i) ∉ ⟨3 -i⟩

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.