Intercepts of Graphs

“I hope you rot in the deepest, darkest, and filthiest pit of hell where you really belong, being tormented day and night watching adds, CNN, MSNBC, and woke movies and series forever,” Apocalypse, Anawim, #justtothepoint.

Recall

Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).

The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ.

Graphing functions involves the visual representation of a curve that reflects the behavior of a mathematical function on a coordinate plane, also known as the Cartesian plane. It is a two-dimensional space defined by two axes - the x-axis (horizontal) and the y-axis (vertical).

A systematic approach to graphing a function begins by constructing a table containing selected input values and their corresponding output values. By extending this table, we can plot the points on the coordinate plane and observe the pattern they form. Connecting these points reveals the shape of the curve, allowing us to gain insights into the behavior of the function across its domain. This process provides a visual means of understanding the relationships between different variables and aids in interpreting the overall characteristics of the function.

Intercepts of Graphs

Definition. The x-intercept of a graph is the point(s) or x-coordinate of any point on the graph that intersects the x-axis. In other words, it is the value of x when the function (y-coordinate or y-value) is zero.

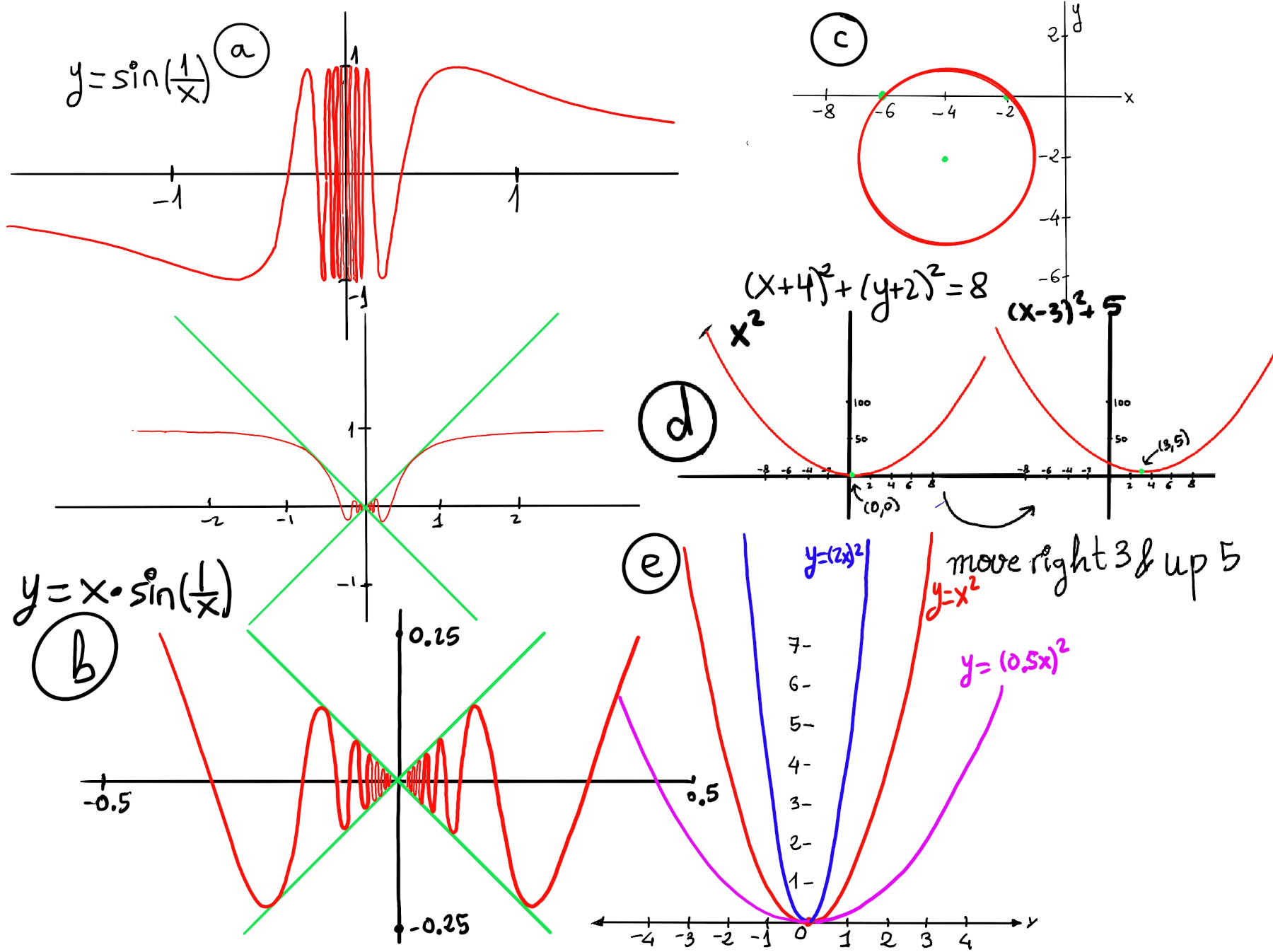
For example, in a linear function defined by y = mx + b, the x-intercept is the solution to the equation 0 = mx +b, that is, x= −b/m. y = 2x -6, the x-intercept is x = 6/2, that is, (3, 0). y = -2x + 5 (Figure iii), the x-intercept is x = -5/-2 = 5/2, that is, (2.5, 0).

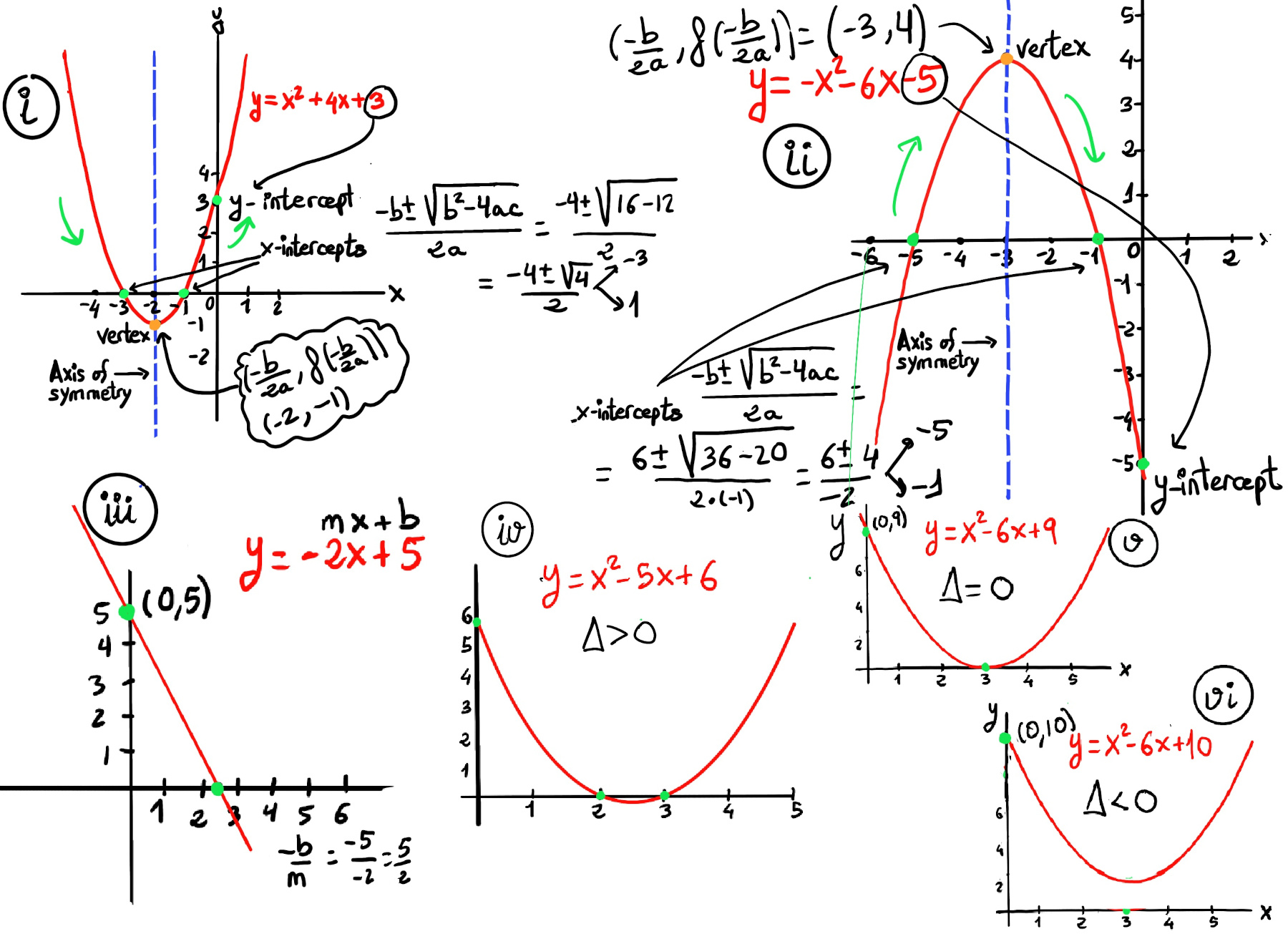
In a quadratic function, we use the quadratic formula, x = $\frac{-b±\sqrt{b^2-4ac}}{2a}$, for the x-intercepts and represent the roots or zeros of the quadratic function. The discriminant (b² -4ac) can be used to calculate the number of x-intercepts and the type of solutions of the quadratic equation.

1. If the value of the discriminant is less than zero, the quadratic equation has two imaginary solutions meaning that the equation does not have any real solution or there are no x-intercepts, e.g., y = $x^2-6x+10, b^2-4ac = 36-40 = -4 < 0,$ (Figure vi).
2. If the value of the discriminant equals zero, then the quadratic equation has a repeated real root meaning the graph of the solution has a single x-intercept, e.g., $x^2-6x+9, b^2-4ac = 36-36 = 0, x = \frac{-b±\sqrt{b^2-4ac}}{2a} = \frac{6±\sqrt{0}}{2} = 3,$ (Figure v)
3. If the value of the discriminant is positive, then the quadratic equation has two real roots meaning the graph of the solution has two distinct intersect, e.g., $x^2-5x+6, b^2-4ac = 25-24 = 0, x = \frac{-b±\sqrt{b^2-4ac}}{2a} = \frac{5±\sqrt{1}}{2}=$ 3 or 2(Figure iv).

Definition. Equivalently, the y-intercept is the y-coordinate of the point whose x-coordinate is 0. In other words, the y-intercept is the point where the graph of the function intersects or crosses the y-axis. Since a function must pass the vertical line test (a function has exactly one output for each input), a function can have, at most, one y-intercept.

Let the equation of a graph be y = -2x + 5, to find the y-intercept, set x = 0 ⇒ y = -2(0) + 5 ⇒ y = 5. Therefore, the y-intercept is (0, 5). In other words, when the equation of a line is written in slope-intercept form (y = mx + b), the y -intercept can be read immediately from the equation, that is, b, e.g., y = -2x + 5 the y-intercept is (0, 5) (Figure iii).

A linear function is a function of the form y = mx + b, where m is the slope of the line, b is the y-intercept, and −b/m the x-intercept.

• Example: 2x -4y = 8. Its alternate form is 4y = 2x -8 ↭ $y = \frac{2x}{4}-\frac{8}{4} ↭ y = \frac{x}{2}-2$, -2 is the y-intercept, and $\frac{-b}{m} = \frac{2}{\frac{1}{2}} = 4$ is the x-intercept.

Besides, for a quadratic equation written in standard form y = ax² +bx +c , the y-intercept is c.

The graph of a quadratic function ax² + bx + c is a parabola. It has an extreme point, called the vertex where the curve changes direction.

If the parabola opens upwards (a > 0), the vertex represents the lowest point on the curve and its y-coordinate is the minimum value of the quadratic function. If the parabola opens downwards (a < 0), the vertex represents the highest point on the curve, and its y-coordinate is the maximum value. In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry $x = \frac{-b}{2a}$, So, the graph of the function is increasing on one side of the axis and decreasing on the other side.

• Let’s find the x- and y-intersect of -2x + 4y = 8. To find the x-intercept, set y = 0 ⇒ -2x = 8 ⇒ x = $\frac{8}{-2}=-4$, that is, (-4, 0). To find the y-intercept, set x = 0 ⇒ 4y = 8 ⇒ y = 2, (0,2), Figure 1.

Linear functions are among the easiest to graph, each graph is just a straight line. To plot a linear function, calculate and mark two points on the graph (choose two points that are easy to calculate), and then draw a straight line that passes through both of them. Typically, you can plot the intercepts in the axes and draw a straight line passing through them using a ruler.

• A completely similar example, 5x + 2y = 10. To find the x-intercept, set y = 0 ⇒ 5x = 10 ⇒ x = $\frac{10}{5}=2$, that is, (2, 0). To find the y-intercept, set x = 0 ⇒ 2y = 10 ⇒ y = 5, that is (0, 5).

Not all graphs necessarily have both intercepts: y = 3 has a y-intercept at (0, 3) and no x-intercept, but x = 1 has a x-intercept at (1, 0) and no y-intercept (Figure 2 and 3 respectively).

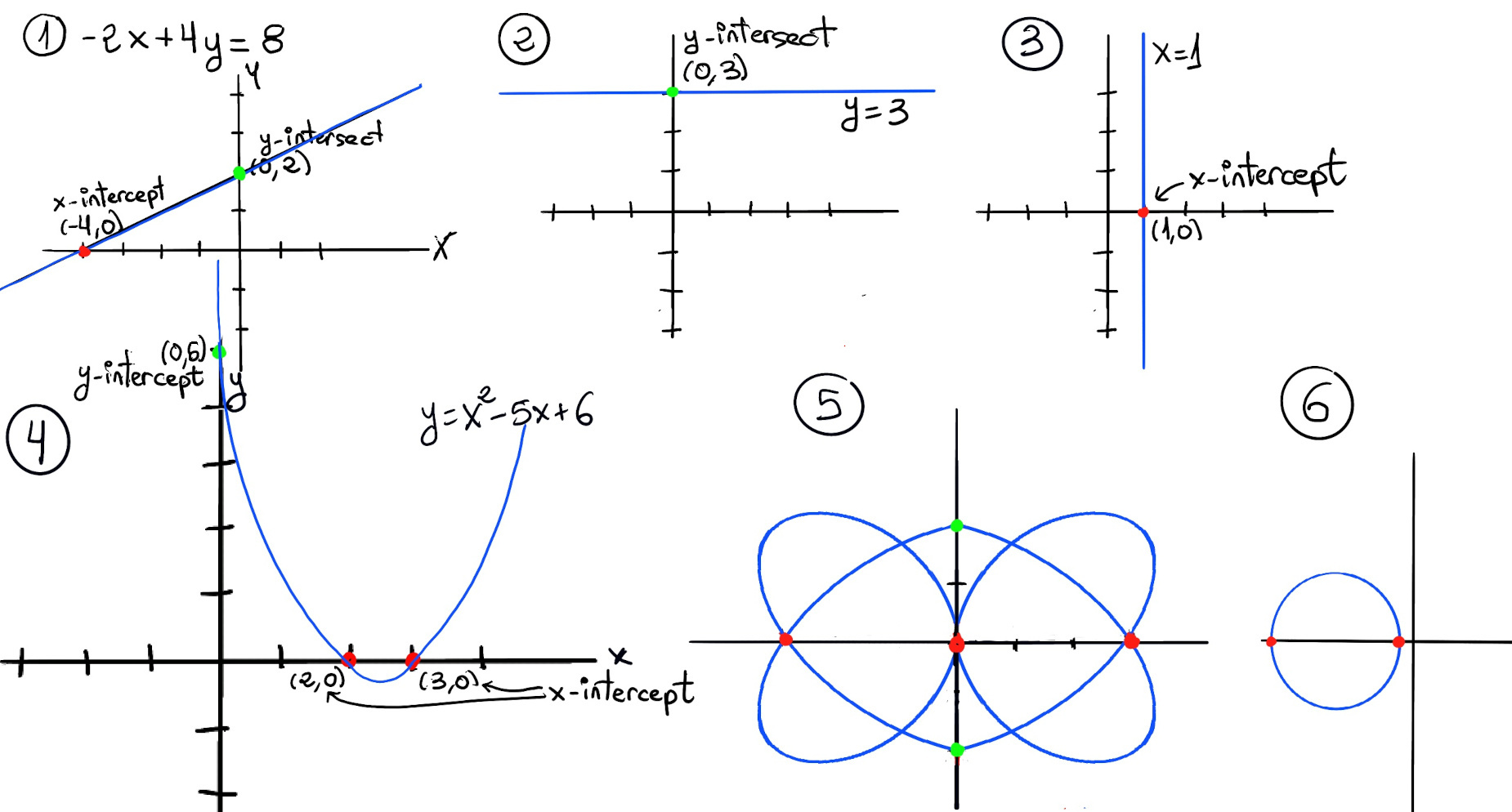The graph y = x² -5x + 6 intersects the x-axis in two places, namely (2, 0) and (3, 0). Its only y-intercept is (0, 6) -Figure 4-.

Finding Intercepts Given the Graph

Figure 5 and 6 illustrate that even though those graphs do not determine functions (they fail to pass the vertical test), they still have x- and y-intercepts (the circle do not have y-intercepts).

The x-intercepts are represented by red circles ((-3, 0), (0, 0), (0, 3) -Figure 5-, (-5, 0), (-1, 0) -Figure 6-) and the y-intercepts by green circles ((0, 2) and (0, -2) -Figure 5-).

If the graph passes through the origin (0,0), it has both an x-intercept and a y-intercept at the origin.

• Extreme cases. The reciprocal function y = 1/x has no intercepts because the reciprocal of 0 is undefined. Therefore, the graph doesn’t cross or touch the x-axis or y-axis. The graph of the sine function, y = sin(x), has infinitely many x-intercepts. The x-intercepts are ···, - 2π, -π, 0, π, 2π, 3π, etc. The y-intercept is (0, 0). Finally, exponential functions y = a^x have no x-intercepts, but they do have single y-intercepts.

• Let’s find the x- and y-intersect of (x + 4)² + (y + 2)² = 8 (Figure c).

x-intercept, y = 0, then solve for x. $(x + 4)^2 + (0 + 2)^2 = 8 ↭ x^2 + 8x +16 + 4 = 8 ↭ x^2 + 8x +12 = 0 ↭ x = \frac{-b±\sqrt{b^2-4ac}}{2a} = \frac{-8±\sqrt{64-48}}{2} = \frac{-8±\sqrt{16}}{2} = \frac{-8±4}{2} =$ -6 and -2 ⇒ the x-intercepts are (-6, 0) and (-2, 0).

y-intercept, y = 0, then solve for x. $(0 + 4)^2 + (y + 2)^2 = 8 ↭ 16 +y^2 +4y + 4 = 8 ↭ y^2 + 4y + 12 = 0, y = \frac{-4±\sqrt{16-48}}{2}$ has no solutions, there are no y-intercepts. (x -a)² + (y -b)² = r² is the standard equation of a circle, the center is (a, b) and the radius is r. In our case, the center is (-4, -2) and the radius is $\sqrt{8} = 2\sqrt{2} ≈ 2.83$.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.