First Isomorphism Theorem

I was pretty sure that she was planning my murder […] A knife? A too much hands-on approach. Pee on the cooking pot? Too gross. Putting me on a cross and throwing darts at me? Too messianic. A grenade? How will I answer some questions? Where did Dad die, Mum, in the kitchen? -Everywhere, he was everywhere, Apocalypse, Anawim, #justothepoint.

First Isomorphism Theorem. Let Φ be a group homomorphism from G to G’. Then, the function or mapping from G/Ker(Φ) to Φ(G), defined by gKer(Φ) → Φ(g) is an isomorphism, i.e., G/Ker(Φ) ≋ Φ(G). In particular, if Φ is onto, G/Ker(Φ) ≋ G’.  

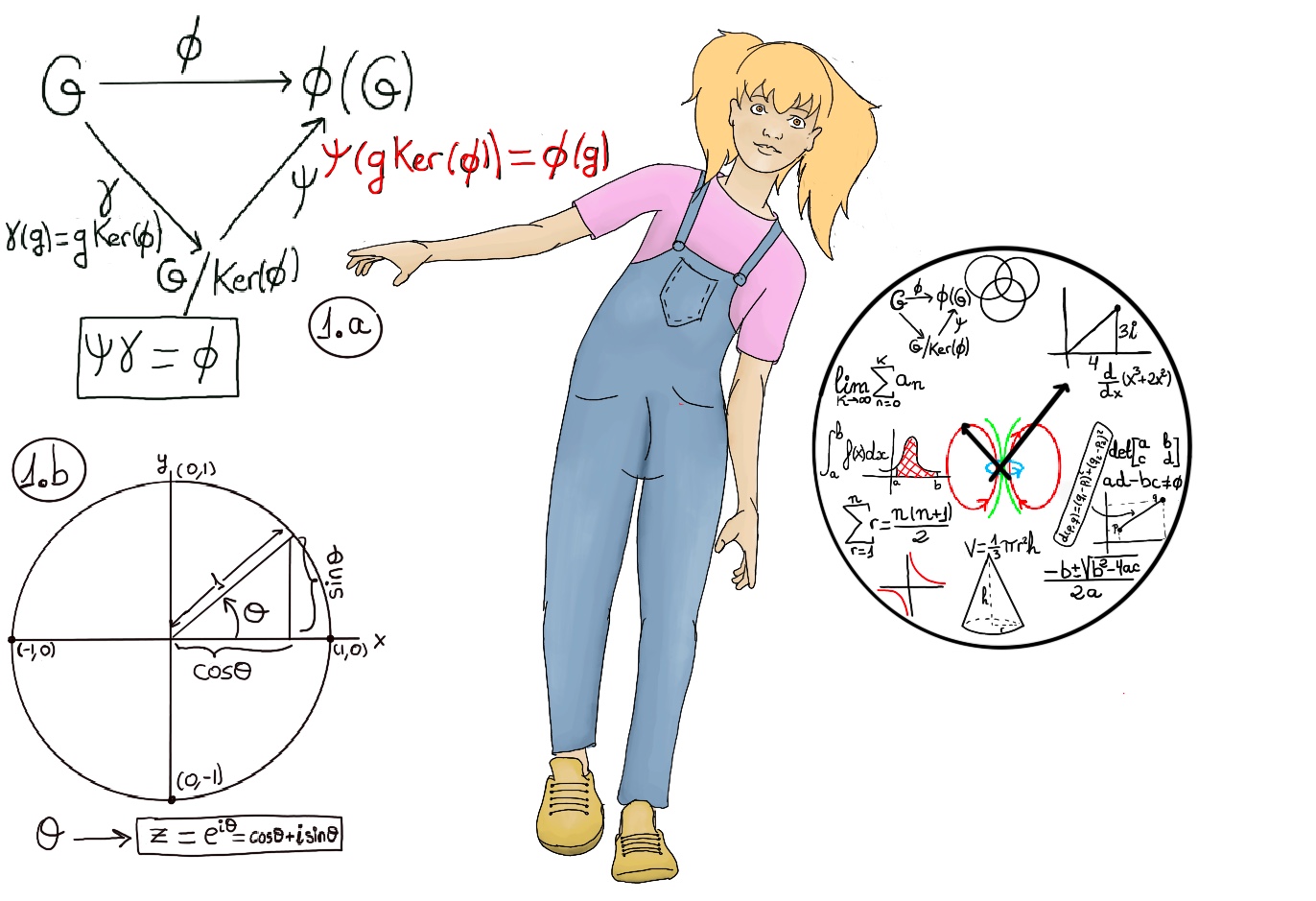
The mapping γ: G → G/Ker(Φ) is defined as γ(g) = gKer(Φ). It is called the natural mapping and is indeed a homomorphism. The Fundamental theorem on homomorphisms or the first isomorphism theorem shows that Ψγ = Φ.

Proof. Let φ: G/Ker(Φ) → Φ(G), φ(aKer(Φ)) = Φ(a).

• is it well defined? ∀a, b ∈ G, aKer(Φ) = bKer(Φ), then φ(aKer(Φ)) = φ(bKer(Φ))? ↭[By definition] ∀a, b ∈ G, aKer(Φ) = bKer(Φ), Φ(a) = Φ(b)? We have already demonstrated it. Recall Homomorphism Property: Φ(a) = Φ(b) if and only if aKer(Φ) = bKer(Φ)
• is it injective or one-to-one? φ(aKer(Φ)) = φ(bKer(Φ)) ⇒ Φ(a) = Φ(b) ⇒ aKer(Φ) = bKer(Φ).
• is it operation-preserving? φ(aKer(Φ)bKer(Φ)) = φ(abKer(Φ)) = Φ(ab) =[By assumption, Φ is an homomorphism] Φ(a)Φ(b) = φ(aKer(Φ))φ(bKer(Φ))
• φ is onto by construction.

Corollary. If Φ is a homomorphism from a finite group G to G', then |Φ(G)| divides both |G| and |G'|.

Proof.

By The First Isomorphism Theorem, G/Ker(Φ) ≋ Φ(G) ⇒ [By Lagrange, |G| = |G/Ker(Φ)]·|Ker(Φ)|] |Φ(G)| divides |G|.

We have previously demonstrated that if H ≤ G, Φ(H) = {Φ(h) | h ∈ H} is a subgroup of G', Φ(H) ≤ G’. In particular, Φ(G) ≤ G’ ⇒ [By Lagrange] |Φ(G)| divides |G’|∎

Examples

• Let G = U(32) = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31}, U₁₆(32) = {1, 17}, U(16) = {1, 3, 5, 7, 9, 11, 13} and Φ: U(32) → U(16), defined by, Φ(x) = [x]_{mod 16}. Ker(Φ) = {x ∈ U(32)| x ≡ 1 (mod 16)} = U₁₆(32) = {1, 17}. Thus, by the first isomorphism theorem, U(32)/U₁₆(32) ≋ Φ(U(32)) =[Φ is onto] U(16).

• Let G be the general linear group, that is, the group of invertibles 2 x 2 matrices with entries from the field of real numbers, and with the group operation being matrix multiplication, G = $GL(2, ℝ) = \bigl\{ {{[\bigl(\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\bigr)]: a, b, c, d ∈ ℝ, ad - bc ≠ 0}} \bigr\}$. The mapping Φ: GL(2, ℝ) → ℝ^*, Φ(A) = det(A) is an homomorphism with Ker(Φ) = SL₂(ℝ), and im(Φ) = ℝ^x. Thus, by the first isomorphism theorem, GL₂(ℝ)/SL₂(ℝ) ≋ ℝ^x.

• Let G = $gl_2(ℝ) = \bigl\{ {{[\bigl(\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\bigr)]: a, b, c, d ∈ ℝ}} \bigr\}$, Φ: gl₂(ℝ) → ℝ, Φ(A) = tr(A). Φ is an homomorphism, onto, and Ker(Φ) = {$(\begin{smallmatrix}a & b\\ c & -a\end{smallmatrix})$ | a, b, c ∈ ℝ} = sl₂(ℝ) = {A ∈ gl₂(ℝ) | tr(A) = 0}. Then, gl₂(ℝ)/sl₂(ℝ) ≋ ℝ.

• Let G = $gl_2(ℝ) = \bigl\{ {{[\bigl(\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\bigr)]: a, b, c, d ∈ ℝ}} \bigr\}$, Φ: gl₂(ℝ) → sl₂(ℝ), $Φ(\begin{smallmatrix}a & b\\ c & d\end{smallmatrix})=(\begin{smallmatrix}a-d & b\\ c & d-a\end{smallmatrix})$. Φ is an homomorphism, onto (∀B ∈ sl₂(ℝ), B = $(\begin{smallmatrix}a & b\\ c & -a\end{smallmatrix})$, Φ(A) = $Φ(\begin{smallmatrix}a & b\\ c & 0\end{smallmatrix}) = (\begin{smallmatrix}a & b\\ c & -a\end{smallmatrix}) = B$, and ker(Φ) = $\bigl\{ {{[\bigl(\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\bigr)]: Φ(\begin{smallmatrix}a & b\\ c & d\end{smallmatrix})=(\begin{smallmatrix}a-d & b\\ c & d-a\end{smallmatrix})=(\begin{smallmatrix}0 & 0\\ 0 & 0\end{smallmatrix})}}\bigr\}$ ⇒[b = c = 0, a - d = 0 ⇒ a = d] $Ker(Φ) = \bigl\{ {{[\bigl(\begin{smallmatrix}a & 0\\ 0 & a\end{smallmatrix}\bigr)]: a ∈ ℝ}}\bigr\}$ ≋ ℝ ⇒ gl₂(ℝ)/ℝ ≋ sl₂(ℝ).

• Let Φ: (ℤ, +) → (ℤ_n, +_n), Φ(m) = [m]_{mod n} is a homomorphism, Φ is onto and Ker(Φ) = ⟨n⟩ = nℤ. By the First Isomorphism Theorem, G/Ker(Φ) ≋ Φ(G), that is, ℤ/⟨n⟩ = ℤ/nℤ ≋ ℤ_n. Besides, ∀m ∈ ℤ_n, the set Φ^-1(m) = {…, m - 2n, m - n, m, m + n, m + 2n, …} = m + nℤ is indeed a coset.

• Φ: ℤ₄ → ℤ₂, [m]₄ → [m]₂ is a homomorphism, Ker(Φ) = ⟨[2]₄⟩ and surjective (Φ([2]₄) = [0]₂, Φ([1]₄) = [1]₂). By the First Isomorphism Theorem, G/Ker(Φ) ≋ Φ(G), that is, ℤ₄/⟨[2]₄⟩ ≋ ℤ₂.

• Φ: ℤ₆ → ℤ₁₅. There are only two possible homomorphisms: 1. Φ([1]₆) = Φ([x]₆) =[0]₁₅ ⇒ Ker(Φ) = ℤ₆, im(Φ) = {[0]₁₅} ⇒ ℤ₆/ℤ₆ ≋ {[0]₁₅} ≤ ℤ₁₅. 2. Φ([1]₆) = [5]₁₅, Φ([x]₆) =[5x]₁₅. Ker(Φ) = {[0]₆, [3]₆} = ⟨[3]₆⟩ ≋ ℤ₂. Im(Φ) = {[0]₁₅, [5]₁₅, [10]₁₅} = ⟨[5]₁₅⟩ ≋ ℤ₃ ⇒ ℤ₆/⟨[3]₆⟩ ≋ ℤ₆/ℤ₂ ≋ ⟨[5]₁₅⟩ ≋ ℤ₃

• The wrapping function takes the real number line and wraps it around the unit circle. W assigns to each θ → e^iθ = cosθ + isinθ. W is an homomorphism from (ℝ, +) onto S¹ = ({z ∈ ℂ: |z| = 1}, ·).

  This map is a homomorphism because the multiplication of unit complex numbers corresponds to addition of angles: Φ(θ₁+θ₂) = e^{i(θ₁+θ₂)} = e^iθ₁e^iθ₂ = Φ(θ₁) + Φ(θ₂)

Ker(Φ) = {θ: e^iθ = 1} = {2πn: n ∈ ℤ} = 2πℤ. In words, the kernel of this homomorphism is the set of all integer multiples of 2π. By the first isomorphism theorem, we have that S¹ = {z ∈ ℂ: |z| = 1} ≋ ℝ/2πℤ.

• Let ℝ[x] be the group of polynomials with coefficients in the real numbers, d/dx: ℝ[x] → ℝ[x], defined by, p(x)→ p’(x). It is an homomorphism because the derivative of a sum of functions is the sum of their derivatives (the sum rule): d/dx(p(x) + q(x)) = p’(x) + q’(x) = d/dx(p(x)) + d/dx(q(x)).

∀p(x) ∈ ℝ[x], p(x) = a₀ + a₁x + a₂x² + ··· + a_nxⁿ, there exists $a_0x + \frac{a_1}{2}x^2+···+\frac{a_n}{n+1}x^{n+1}$ such that $\frac{d}{dx}(a_0x + \frac{a_1}{2}x^2+···+\frac{a_n}{n+1}x^{n+1})= a_0 + a_1x + ··· a_n x ⇒ im(\frac{d}{dx})=\mathbb{R[x]}$. Besides, $Ker(\frac{d}{dx})$ = ℝ. By the First Isomorphism Theorem, ℝ[x]/ℝ ≋ ℝ[x].

• Let G = D_n = {e, r, r², ···, r^n-1, r, sr, sr², ···, sr^n-1} = ⟨r, s | rⁿ = s² = e, rs = sr^n-1⟩, the dihedral group. Φ: D_n → ℤ₂ be the map given by, r → 0, s → 1. We need to check that the following equations are satisfied:

1. rⁿ = e. Φ(rⁿ) = 0, but also Φ(rⁿ) = 0 + 0 + ··_n·· + 0 = 0.
2. Φ(s²) =[s² = 2] Φ(e) = 0, but also Φ(s²) = Φ(s) + Φ(s) = 1 +₂ 1 = 0.
3. Φ(rs) = Φ(sr^n-1). Φ(rs) = Φ(r) + Φ(s) = 0 + 1 = 0. Φ(sr^n-1) = Φ(s) + Φ(r) + ··_n-1·· Φ(r) = 1 + 0 + ··_n-1·· + 0 = 1.

Futhermore, Φ is obviously surjective, and Ker(Φ) = ⟨r⟩ because any arbitrary rotation r^k satisfies Φ(r^k) = kΦ(r) = 0, and any arbitrary reflection sr^k, Φ(sr^k) = Φ(s) + kΦ(r) = 1 + k·0 = 1 ⇒ D_n/⟨r⟩ ≋ ℤ₂. Futhermore, D_n = Ker(Φ) ∪ sKer(Φ) = ⟨r⟩ ∪ {s, r, sr, sr², ···, sr^n-1}.

In other words, our homomorphism could have been previously defined by,

$Φ(x) = \begin{cases} 0, &x~is~a~rotation \\ 1, &x~is~a~reflection \end{cases}$

• Let G = D_n = {e, r, r², ···, r^n-1, r, sr, sr², ···, sr^n-1} = ⟨r, s | rⁿ = s² = e, rs = sr^n-1⟩, the dihedral group. Φ: D_n → ℤ_n be the map given by, r → 1, s → 0. However, this is not an isomorphism because Φ(rs) ≠ Φ(sr^n-1). Φ(rs) = Φ(r) + Φ(s) = 1. Φ(sr^n-1) = Φ(s) + (n-1)Φ(r) = 0 +(n-1)·1 = n -1, but 1 ≇ n - 1 (mod n) unless n = 2.

• Let G = D_2n = ⟨r, s | r²ⁿ = s² = e, rs = sr^2n-1⟩. Φ: D_2n → ℤ₂ be the map given by, r → 1, s → 0. We need to check that the following equations are satisfied:

1. r²ⁿ = e. Φ(r²ⁿ) = Φ(e) = 0. Φ(r²ⁿ) = 2n·Φ(r) = 2n·1 =_ℤ2 0.
2. s² = e. Φ(s²) = 2·Φ(s) = 2·0 = 0.
3. rs = sr^{2n -1}. Φ(rs) = Φ(r) + Φ(s) = 1 + 0 = 1. Φ(sr^2n-1) = Φ(s) +(2n -1)Φ(r) = 0 + (2n -1)·1 = 2n -1 =_ℤ2 = -1 =_ℤ2 = 1.

It is obviously surjective. Ker(Φ) = {e, r², r⁴, ···, r^2n-1, s, sr², sr⁴, ···, sr^2n-1} = ⟨r², s⟩ = ⟨s, r² | s² = (r²)ⁿ = e, r²s =[rs = sr^2n-1, r²s = r(rs) = rsr^2n-1 = (rs)r^2n-1 = sr^2n-1r^2n-1] s(r²)^2n-1⟩ ≋ D_n. Therefore, D_2n/Ker(Φ) ≋ D_2n/⟨r², s⟩ ≋ D_2n/D_n ≋ ℤ₂.

• Let G = D₆ = ⟨r, s | r⁶ = s² = e, rs = sr⁵⟩. Φ: D₆ → S₆, r → (123456), s → (16)(25)(34). Φ(r⁶)

is it homomorphism? Φ(r⁶) = (123456)⁶ = (1) = Φ(e). Φ(s²) = (16)(25)(34)(16)(25)(34) = (1) = Φ(e). Φ(rs) = (123456)(16)(25)(34) = (26)(35). Φ(sr⁵) = Φ(s)Φ(r)⁵ = (16)(25)(34)(123456)⁵ = (16)(25)(34)(165432) = (26)(35) = Φ(rs).

Besides, im(Φ) = ⟨(123456), (16)(25)(34)⟩ and Ker(Φ) = {e} (it is left as an exercise) ⇒ D₆ ≋ im(Φ) = ⟨(123456), (16)(25)(34)⟩.

• Let S_n be the symmetric group of n letter, and let Φ: S_n → ℤ₂ be the homomorphism defined by, $Φ(σ) = \begin{cases} 0, &σ~ is~ an~ even~ permutation\\\\ 1, &σ~ is~ an~ odd~ permutation \end{cases}$

Φ is an homomorphism, onto, and Ker(Φ) = A_n ⇒ S_n/A_n ≋ ℤ₂.

• Exercises (hints).

1. Φ: ℝ → ℝ^x+, Φ(x) = 2^x. Φ is an homomorphism, onto (∀y ∈ ℝ^x+, Φ(log₂y) = 2^log₂y = y), and Ker(Φ) = {x ∈ ℝ| 2^x = 1} = {0} ⇒ ℝ ≋ ℝ^x+.
2. Φ: ℤ → ℂ^x, Φ(n) = iⁿ. im(Φ) = {1, i, -1, -i} = ⟨i⟩, ker(Φ) = 4ℤ, and ℤ/4ℤ ≋ ⟨i⟩ ≤ ℂ^x.
3. Φ: ℤ → ℂ^x, Φ(m) = e^2πim/n, Im(Φ) = {1, w, w², ···, w^n-1} = ⟨w⟩ ≋ ℤ_n where w = e^2πi/n, Ker(Φ) = nℤ (m ∈ Ker(Φ) ↭ e^2πim/n = 1 ↭ cos(2πim/n) = 1, sin(2πim/n) = 0 ↭ n | m) ⇒ ℤ/nℤ ≋ ⟨w⟩ ≋ ℤ_n ≤ ℂ^x.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.