Group Homomorphism

“Wow! So you use Internet Explorer in Windows, you must like it nice and slow,” I told one of my friends in the laboratory. “Wow! So you use vim in Linux, you must like it rough and tough,” Sussanne replied with a smirking smile, Apocalypse, Anawim, #justtothepoint.

Definitions

In algebra, a homomorphism (from ὁμός, “homo” meaning same and μορφή, “morph”, shape or form) is a structure-preserving map between two algebraic structures of the same type, such as two groups, two rings, or two vector spaces.

In this chapter, we will give a more specific definition. A homomorphism Φ from a group G to a group G’ is a function or a mapping from (G, ∘) to (G', *) that preserves the operations of the groups; this means a map, Φ: G → G’ between both groups that satisfies Φ(a∘b) = Φ(a)*Φ(b) for every pair a, b of elements of G, that is, ∀a, b ∈ G (Figure 1.a. & Figure 1.b.).

 

💡A group homomorphism is a function, satisfying a few “natural” properties, between two groups that identifies similarities between them. Consider the groups ℤ and ℤ/2ℤ. The integer numbers can be partitioned into two subsets: even numbers and odd numbers. Let’s define Φ: (ℤ, +) → (ℤ/2ℤ, +_{mod 2}), Φ(n) = n mod 2, e.g., Φ(1) = Φ(3) = Φ(any arbitrary even number) = 1, Φ(2) = Φ(4) = Φ(any arbitrary odd number) = 0 (Figure 1.b.). Notice that even + even = even (0 + 0 ≡ 0 mod 2), even + odd = odd (0 + 1 ≡ 1 mod 2), odd + even = odd (1 + 0 ≡ 1 mod 2), and odd + odd = even (0 + 0 ≡ 0 mod 2).

We say that this homomorphism maps elements of ℤ to elements of ℤ/2ℤ. The group from which a function originates is the domain (ℤ in our example). The group into which the function maps is the codomain (ℤ/2ℤ). Φ: (G, ∘) → (G’, *) is an homomorphism if and only if Φ(a∘b) = Φ(a)*Φ(b), ∀a, b∈ G. Note that the operation a ∘ b is occurring in the domain while Φ(a)*Φ(b) occurs in the codomain.

Not every function from one group to another is a homomorphism. The condition Φ(a∘b) = Φ(a)*Φ(b), ∀a, b∈ G means that the map Φ preserve the structure of G.

Next, let’s consider the additive group of integers modulo 4 (ℤ/4ℤ, +_{mod 4}) and the multiplicative group ({1, -1, i, -i}, ·) formed by the fourth roots of unity, and their Cayley tables.

Consider Φ : (ℤ/4ℤ, +_{mod 4}) → ({1, -1, i, -i}, ·), Φ(0) = 1, Φ(1) = i, Φ(2) = -i, and Φ(3) = -i. Φ is not just an homomorphism, it is indeed an isomorphism, that is, a bijective (both injective and surjective) homomorphism. An automorphism is an isomorphism from a group to itself.

Futhermore, we can observe the following:

1. They are both cycle groups. (ℤ/4ℤ, +_{mod 4}) = ⟨1⟩ and {1, -1, i, -1} = ⟨i⟩ = {i⁰ = 1, i¹ = i, i² = -1, i³ = i}
2. Φ carries the identity (Φ(0) = 1), and the generator (Φ(1) = i).
3. They’re identical groups, both Cayley tables are exactly the same, i.e. up to relabeling the group elements.

The kernel of a homomorphism Φ is the set of elements in G which are mapped to the identity in G'; that is, Ker(Φ) = {a ∈ G | Φ(x) = e’} where e’ is the identity in G’. The elements in the codomain that the function maps to are called the image of the function, denoted Im(Φ), that is, Im(Φ) = Φ(G) = {Φ(g) | g ∈ G}.

Examples

• Any isomorphism is a homomorphism. An isomorphism is also onto and one-to-one. The kernel of an isomorphism is the trivial subgroup.

• Let Φ: G → G’ be defined by Φ(a) = e’ ∀a ∈ G. Φ(ab) = e’ = e’e’ = Φ(a)Φ(b) ∀a, b ∈ G. This is called the trivial homomorphism and Ker(Φ) = G.

• Let Φ: ℤ → ℤ be defined by Φ(n) = 2n, Φ is a homomorphism. Φ(n + m) = 2(n + m) = 2n + 2m = Φ(n) + Φ(m). Ker(Φ) = {n ∈ ℤ: Φ(n) = 2n = 0} = {0}.

• Let Φ: ℤ → ℤ₅ = {[0], [1], [2], [3], [4]}, Φ(n) = n mod 5 = [n]_{mod 5} is a homomorphism, Φ(m + m’) = [m + m’]_{mod 5} = [m]_{mod 5} + [m’]_{mod 5} = Φ(m) + Φ(m’). Ker(Φ) = {n ∈ ℤ| Φ(n) = [0]} = {n ∈ ℤ: n ≡ 0 (mod 5)} = 5ℤ (Figure 1.b., n = 5). 

• Let’s generalize the previous result. Residue modulo n of an integer. Let Φ: (ℤ, +) → (ℤ_n, +_n), Φ(m) = [m]_{mod n} is a homomorphism: Φ(m + m’) = [m + m’]_{mod n} = [m]_{mod n} + [m’]_{mod n} = Φ(m) + Φ(m’).

Φ is surjective, Φ(ℤ) = img(Φ) = ℤ_n because ∀ 0 ≤ m ≤ n-1, [m] ∈ ℤ_n, Φ(m) = [m]. m ∈ Ker(Φ) ↭ Φ(m) = [0] ↭ m ≡ 0 (mod n). Therefore, Ker(Φ) = ⟨n⟩ = nℤ.

• Φ: ℤ₄ → ℤ₂, [m]₄ → [m]₂. is it well-defined? Suppose [m₁]₄ = [m₂]₄ ⇒ [m₁ - m₂]₄ = [0]₄ ⇒ m₁ -m₂ = 0 (mod 4) ⇒ [∃k ∈ ℤ: m₁ - m₂ = 4k ⇒ m₁ - m₂ = 2(2k)] [m₁ - m₂]₂ = [0]₂ ⇒ [m₁]₂ = [m₂]₂.

Besides, it is an homomorphism, Φ([m]₄ + [m’]₄) = Φ([m + m’]_{mod 4}) = [m + m’]_{mod 2} = [m]_{mod 2} + [m’]_{mod 2} = Φ(m) + Φ(m’). Φ is surjective, because Φ([0]₄) = [0]₂ and Φ([1]₄) = [1]₂. Ker(Φ) = {[m]₄ ∈ ℤ₄ | Φ([m]₄) = [m]₂ = [0]₂} = {[0]₄, [2]₄} = ⟨[2]₄⟩.

• Let G be any arbitrary group, we define Φ: ℤ → G, Φ(n) = gⁿ where g ∈ G is fixed. Φ is a homomorphism, Φ(n + m) = gⁿ⁺ⁿ = gⁿg^m = Φ(n)Φ(m).

• Let G be the general linear group, that is, the group of invertible 2 x 2 matrices with entries from the field of real numbers, and with the group operation being matrix multiplication, G = $GL(2, ℝ) = \bigl\{ {{[\bigl(\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\bigr)]: a, b, c, d ∈ ℝ, ad - bc ≠ 0}} \bigr\}$. The mapping Φ: GL(2, ℝ) → ℝ^*, Φ(A) = det(A) is an homomorphism, Φ(AB) = det(AB) = det(A)·det(B)) = Φ(A)Φ(B).

A ∈ Ker(det) ↭ det(A) = 1 ↭ A ∈ SL₂(ℝ) = {$GL(2, ℝ) = \bigl\{ {{[\bigl(\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\bigr)]: a, b, c, d ∈ ℝ, ad - bc = 1}} \bigr\}$}, that is, the group of 2 x 2 matrices with determinant one.

What is im(Φ)?

1. x > 0 ⇒ $\sqrt{x} > 0 ⇒ det(\begin{smallmatrix}\sqrt{x} & 0\\ 0 & \sqrt{x}\end{smallmatrix}) = x$.
2. x < 0 ⇒ $\sqrt{-x} > 0 ⇒ det(\begin{smallmatrix}0 & \sqrt{-x}\\ \sqrt{-x} & 0\end{smallmatrix}) = x$ ⇒ im(Φ) = Φ(GL₂(ℝ)) = ℝ^x.

• Let G = $gl_2(ℝ) = \bigl\{ {{[\bigl(\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\bigr)]: a, b, c, d ∈ ℝ}} \bigr\}$, Φ: gl₂(ℝ) → ℝ, Φ(A) = tr(A), the trace of a square matrix is the sum of elements of the main diagonal of A.

Φ is a homomorphism. $Φ((\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}) + (\begin{smallmatrix}a’ & b’\\ c’ & d’\end{smallmatrix})) = a + d + a’ + d’ = Φ((\begin{smallmatrix}a & b\\ c & d\end{smallmatrix})) + Φ((\begin{smallmatrix}a’ & b’\\ c’ & d’\end{smallmatrix}))$. Φ is onto, ∀a ∈ ℝ, $Φ((\begin{smallmatrix}a & b\\ c & 0\end{smallmatrix}))$ = a. Ker(Φ) = {$(\begin{smallmatrix}a & b\\ c & -a\end{smallmatrix})$ | a, b, c ∈ ℝ} = sl₂(ℝ) = {A ∈ gl₂(ℝ) | tr(A) = 0}.

💣 However, Φ: GL₂(ℝ) → ℝ defined by Φ(A) = tr(A) is not an homomorphism since it maps the identity $Φ((\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}))$ to 2, which is not the identity in ℝ. The general linear group GL(2, ℝ) is defined as the group of invertible 2 x 2 matrices with entries from the field of real numbers, and with the group operation being matrix multiplication. gl₂(ℝ) is the group of 2 x matrices with entries from the field of real numbers, and with the group operation being matrix addition, so the identity is $(\begin{smallmatrix}0 & 0\\ 0 & 0\end{smallmatrix})$, and tr maps the identity to zero, which is the identity in ℝ.

• Let S_n be the symmetric group of n letter, and let Φ: S_n → ℤ₂ be the homomorphism defined by, $Φ(σ) = \begin{cases} 0, &σ~ is~ an~ even~ permutation\\\\ 1, &σ~ is~ an~ odd~ permutation \end{cases}$

Φ is an homomorphism because every permutation σ is a product of transpositions, and therefore these are these different options:

1. σ₁ and σ₂ even, Φ(σ₁σ₂) =[even + even = even] 0 =[Additive notation] Φ(σ₁) + Φ(σ₂) = 0 + 0.
2. σ₁ and σ₂ odd, Φ(σ₁σ₂) =[odd + odd = even] 0 =_ℤ2 Φ(σ₁) + Φ(σ₂) = 1 + 1.
3. σ₁ even and σ₂ odd, Φ(σ₁σ₂) =[even + odd = even] 1 =_ℤ2 Φ(σ₁) + Φ(σ₂) = 0 + 1.
4. σ₁ odd and σ₂ even, Φ(σ₁σ₂) =[odd + even = even] 1 =_ℤ2 Φ(σ₁)Φ(σ₂) = 1 + 0.

Φ is surjective, e.g., (12) → 1, () → 0. Ker(Φ) = {σ ∈ S_n | σ is even} = A_n, the alternating group of even permutations.

• Let Φ: ℂ* → ℝ⁺, the group of positive real numbers under multiplication, defined by a + bi → |a + bi| = $\sqrt{a^2+b^2}$. Φ((a + bi)(c + di))= Φ((ac -bd) + (ad +bc)i) = $\sqrt{(ac-bd)^2+(ad+bc)^2} = \sqrt{a^2c^2-2abcd+b^2d^2+a^2d^2+2abcd+b^2c^2} = \sqrt{a^2c^2+b^2d^2+a^2d^2+b^2c^2} = \sqrt{a^2(c^2+d^2)+b^2(c^2+d^2)} = \sqrt{(a^2+b^2)(c^2+d^2)} = \sqrt{a^2+b^2}\sqrt{c^2+d^2}$ = Φ(a + bi)Φ(c + di) ⇒ Φ is an homomorphism. Besides, Φ is onto since ∀r ∈ ℝ⁺, r is in ℂ*, and Φ(r) = r. Ker(Φ) = {z ∈ ℂ*: |z| = 1}.
• The sign function, sign: ℝ* → {1, -1} defined by $ sign(x) = \frac{x}{|x|} = \begin{cases} 1, &if~ x~>~0\\\\ -1, &if~ x~<~0 \end{cases}$

sign(xy) = 1 if x and y are both positive or negative, and -1 if one of them is positive and negative, thus sign(xy) = sign(x)·sign(y). Ker(sign) = ℝ⁺, the set of all positive real numbers.

• Let (ℝ[x], +) be the additive group of all polynomials with real coefficients. The mapping Φ: ℝ[x] → ℝ[x], Φ(f) = f’ is a homomorphism. Φ(f + g) = (f + g)’ = f’ + g’ = Φ(f) + Φ(g). Ker(Φ) = {f: f(x) = k, k ∈ ℝ}, i.e., constant polynomials, that is, polynomials having its highest degree zero. Besides, the function Φ: ℝ[x] → ℝ defined by Φ(f) = f(a) is a homomorphism, too. It is called an evaluation homomorphism.
• Φ: (ℝ*, ·) → (ℝ*, ·), Φ(x) = x^2 is a homomorphism. Ker(Φ) = {1, -1}. The reader should notice that it is an homomorphism under multiplication, (ℝ*, ·) because $Φ(ab)=(ab)^{2}=a^{2}b^{2}=Φ(a)Φ(b)$, but it is not under addition (ℝ, +): $Φ(a+b)=(a+b)^{2}=a^{2}+b^{2}+2ab≠Φ(a)Φ(b)$.
• Let S¹ be the unit circle in ℂ with multiplication as the group operation, S¹ = {z | |z| = 1}. Let Φ: (ℝ, +) → S¹, Φ(r) = e^i2πr is a homomorphism: Φ(r+s) = e^i2π(r+s) = e^i2πr+i2πs =[exp(z₁ + z₂) = exp(z₁)(exp(z₂)] e^i2πre^i2πs = Φ(r)Φ(s).

Φ is onto, since if z ∈ S¹ ⇒ z = e^iθ = e^i2π(2πθ) = Φ(θ2π). r ∈ Ker(Φ) ↭ Φ(r) = 1 ↭ e^2πri = 1 ↭ cos(2πr) + isin(2πr) = 1 ↭ cos(2πr) = 1 and sin(2πr) = 0 ↭ r ∈ ℤ ⇒ Ker(Φ) = ℤ.

Properties

Let Φ be a homomorphism from a group G to another, G’, and let a, b be two arbitrary elements of G. Let H be a subgroup of G, H ≤ G. Then, the following statements hold true:

• Φ carries the identity of G to G', that is, Φ(e) = e'.

Proof:

Φ(e) = Φ(e·e) = Φ(e)Φ(e) ⇒ Φ(e) = Φ(e)Φ(e) ⇒ e’ = Φ(e)Φ(e)^-1 = (Φ(e)Φ(e))Φ(e)^-1 = Φ(e)

• ∀n ∈ ℤ, Φ(aⁿ) = (Φ(a))ⁿ. Proof. They are both identical to the proof shown about isomorphisms
• If |a| < ∞, then |Φ(a)| divides |a|.

Proof.

If |a| is finite ⇒ ∃n ∈ ℤ: aⁿ = e ⇒ Φ(aⁿ) = [Φ(aⁿ) = (Φ(a))ⁿ] (Φ(a))ⁿ = Φ(e) =[Φ carries the identity] e’ where e’ is the identity of G’. Therefore, (Φ(a))ⁿ = e’ ⇒ |Φ(a)| divides n ( = |a|) ∎

Last step: Suppose m = |Φ(a)| ⇒ ∃q, r: n = mq + r, 0 ≤ r < m ⇒ (Φ(a))^r = (Φ(a))ⁿ(Φ(a))^-mq = (Φ(a))ⁿ((Φ(a))^m)^-q = [(Φ(a))ⁿ = e’, m = |Φ(a)|] e’·e’ = e’ ⇒ [m = |Φ(a)| and 0 ≤ r < m] r = 0 ⇒ m | n.

Examples

• Find all homomorphisms from ℤ₆ to ℤ₁₅.

Recall that to specify a group homomorphism Φ: ℤ_m → ℤ_n is enough to say what the value of Φ(1) is. Remember also that for a group homomorphism Φ : G → G’, Φ(e) = e'.

Define Φ:ℤ₆ to ℤ₁₅ by Φ([x]₆) = Φ([1+··+_x+··+1]₆) = [Φ([1]₆)+··+_x+··+Φ([1]₆)]₁₅ = [Φ([1]₆)x]₁₅ = [mx]₁₅.

|Φ(1)| | |1| ⇒ |Φ(1)| | 6 ⇒ |Φ(1)| = {1, 2, 3, 6}. Since Φ(1) ∈ ℤ₁₅, the order of Φ(1) has to divide 15, too, so the options are |Φ(1)| = {1, 3}. Besides, we know that |a^m| = |⟨a^m⟩| = $\frac{n}{gcd(m, n)}=\frac{15}{gcd(15, m)}$. Therefore, in ℤ₁₅, these are the options:

1. The only element in ℤ₁₅ of order 1 is 0, |[0]₁₅| = 1, Φ([1]₆) = Φ([0·x]₆)_{x = 1} =[0]₁₅ ⇒ Ker(Φ) = ℤ₆, im(Φ) = {[0]₆}
2. The only elements in ℤ₁₅ of order 3 are 5 and 10, |[5]₁₅| = |[10]₁₅| = 3. Φ([1]₆) = [5]₁₅, Φ([x]₆) =[5x]₁₅, e.g., Φ([2]₆) = [10]₁₅, Φ([3]₆) = [0]₁₅, Φ([4]₆) = [20]₁₅ = [5]₁₅. Ker(Φ) = {[0]₆, [3]₆} = ⟨[3]₆⟩. Im(Φ) = {[0]₁₅, [5]₁₅, [10]₁₅} = ⟨[5]₁₅⟩ ≋ ℤ₃. Or alternatively Φ([1]₆) = [10]₁₅.

• Find all homomorphisms from ℤ₂₄ to ℤ₁₈.

Define Φ:ℤ₂₄ to ℤ₁₈ by Φ([x]₂₄) = [mx]₁₈ for some [m]₁₈ ∈ ℤ₁₈.

|Φ(1)| | |1| ⇒ |Φ(1)| | 24 ⇒ |Φ(1)| = {1, 2, 3, 4, 6, 8, 12}. Since Φ(1) ∈ ℤ₁₈, the order of Φ(1) has to divide 18, too, so the options are |Φ(1)| = {1, 2, 3, 6}.

We know that |a^m| = |⟨a^m⟩| = $\frac{n}{gcd(m, n)}=\frac{18}{gcd(18, m)}$. Therefore, in ℤ₁₈, these are the options:

1. |3| = |15| = 6, Φ([x]₂₄) =[3x]₁₈, Φ([x]₂₄) =[15x]₁₈.
2. |6| = |12| = 3, Φ([x]₂₄) =[6x]₁₈, Φ([x]₂₄) =[12x]₁₈.
3. |9| = 2, Φ([x]₂₄) =[9x]₁₈.
4. |0| = 1, Φ([x]₂₄) =[0]₁₈.

• Can there be a homomorphism from ℤ₄ × ℤ₄ onto ℤ₈?

Suppose for the sake of contradiction, Φ: ℤ₄ × ℤ₄ → ℤ₈, Φ surjective ⇒ ∃x ∈ ℤ₄ × ℤ₄: Φ(x) = 1 ∈ ℤ₈ ⇒ |Φ(x)| = 8 ⊥ We know that |a| < ∞, then |Φ(a)| divides |a|. Besides, |Φ(x)| = 8 divides |x| ≤ 4 (∀x ∈ ℤ₄ × ℤ₄, |x| = 1, 2 or 4).

• The kernel of a homomorphism is a subgroup of G, Ker(Φ) ≤ G.

Proof.

e ∈ Ker(Φ) because Φ carries the identity, Φ(e) = e'.

∀a, b ∈ Ker(Φ), ab^-1 ∈ G, Φ(ab^-1) = [Φ preserves the group operation] Φ(a)Φ(b^-1) = [∀n ∈ ℤ, Φ(aⁿ) = (Φ(a))ⁿ. ] Φ(a)Φ(b)^-1 = [a, b ∈ Ker(Φ)] e’e’^-1 = e’ ⇒ ab^-1 ∈ Ker(Φ).∎

• Φ(a) = Φ(b) ↭ aKer(Φ) = bKer(Φ).

Proof.

⇒) Suppose Φ(a) = Φ(b) ⇒ [Multiplying both sides by Φ(b)^-1] (Φ(b))^-1Φ(a) = e’ ⇒[Φ homomorphism ⇒ Φ(aⁿ) = (Φ(a))ⁿ] Φ(b^-1)Φ(a) = e’ ⇒ [Φ preserves group operations] Φ(b^-1a) = e’ ⇒ b^-1a ∈ Ker(Φ) ⇒ [H ≤ G, aH = bH iff a^-1b ∈ H] aKer(Φ) = bKer(Φ).

⇐) Conversely, aKer(Φ) = bKer(Φ) ⇒[H ≤ G, aH = bH iff a^-1b ∈ H] b^-1a ∈ Ker(Φ) ⇒ Φ(b^-1a) = e’ ⇒[Repeating the same argument] (Φ(b))^-1Φ(a) = e’ ⇒ Φ(a) = Φ(b)∎

• If Φ(a) = a', then the inverse image of a' is a coset of the kernel where every element has the same image a', Φ^-1(a’) = {x ∈ G | Φ(x) = a’} = aKer(Φ).

💡The Kernel (preimage of the identity, i.e., Ker(Φ) = Φ^-1{e}) is a subgroup, and all other preimages are cosets of the Kernel. Please read an example that illustrates this fact.

Proof.

Φ(a) = a’. First, let’s prove that Φ^-1(a’) ⊆ aKer(Φ).

Let x ∈ Φ^-1(a’), x ∈ aKer(Φ)?

x ∈ Φ^-1(a’) = {x ∈ G | Φ(x) = a’} ⇒ Φ(x) = a’ = Φ(a) ⇒ [Previous property, Φ(a) = Φ(b) if and only if aKer(Φ) = bKer(Φ)] xKer(Φ) = aKer(Φ) ⇒ [aH = bH iff a ∈ bH] x ∈ aKer(Φ).

Conversely, let’s try to prove that aKer(Φ) ⊆ Φ^-1(a’). ∀x ∈ Ker(Φ), ax ∈ Φ^-1(a’)?

x ∈ Ker(Φ) ⇒ Φ(x) = e’ ⇒ Φ(ax) =[Φ homomorphism] Φ(a)Φ(x) = a’e’ = a’ ⇒ [By definition] ax ∈ Φ^-1(a’)∎

• Φ(H) = {Φ(h) | h ∈ H} is a subgroup of G', Φ(H) ≤ G’.
• The homomorphic image of a cyclic group is cyclic; that is, if H is cyclic, then Φ(H) is cyclic. In particular, if g ∈ G is a generator of G, then Φ(g) generates Im(G).

∀g’ ∈ Im(G) ⇒[G = ⟨g⟩] ∃n: Φ(gⁿ) = g’ ⇒ (Φ(g))ⁿ = g’. Therefore, ∀g’ ∈ Im(G), ∃n: g’ = (Φ(g))ⁿ ⇒ Im(G) = ⟨Φ(g)⟩.

Besides, if we know where a homomorphism maps the generators of G, we can determine where it maps all elements of G, Φ: ℤ₃ → ℤ₆ is completely determined by Φ(1), because Φ(n) = Φ(1 + 1 + ··_n·· + 1) = Φ(1) + Φ(1) + ··_n·· + Φ(1), e.g., Φ(1) = 4 ⇒ Φ(2) = Φ(1) + Φ(1) = 4 +_{mod 6} 4 = 2, Φ(0) = Φ(1 + 1 + 1) = 4 +_{mod 6} 4 +_{mod 6} 4 = 0.

G = ⟨a, b⟩, Φ: G → H. Suppose that we know Φ(a) and Φ(b). Using this information we can determine the image of any element in G, e.g., Φ(a³b²a) = Φ(a)Φ(a)Φ(a)Φ(b)Φ(b)Φ(a).

Can there be a homomorphism from ℤ₁₆ onto ℤ₂ × ℤ₂?

Nope. Suppose for the sake of contradiction Φ: ℤ₁₆ → ℤ₂ × ℤ₂, Φ surjective ⇒ [ℤ₁₆ = ⟨1⟩, is cyclic] Φ(ℤ₁₆) =[By assumption, Φ is onto] ℤ₂ × ℤ₂ is cyclic ⊥

Important Example

What are the group homomorphisms from ℤ₁₂ to ℤ₁₀? These results have been demonstrated or they will be proven in the following articles.

1. Ker(Φ) ≤ ℤ₁₂ ⇒[By Lagrange’s Theorem] |Ker(Φ)| divides 12 ⇒ |Ker(Φ)| = 1, 2, 3, 4, 6 or 12.
2. First Isomorphism Theorem: ℤ₁₂/Ker(Φ) ≋ Φ(ℤ₁₂) and Φ(ℤ₁₂) ≤ ℤ₁₀ ⇒[By Lagrange’s Theorem] |G/Ker(Φ)| = |G|/|Ker(Φ)| = 12/|Ker(Φ)| divides 10 ⇒ 12/|Ker(Φ)| = 1, 2, 5 or 10.
3. 1 & 2 ⇒ |Ker(Φ)| = 6 or 12.
4. If |Ker(Φ)| = 12 ⇒ G = Ker(Φ) and Φ is the trivial homomorphism.
5. If |Ker(Φ)| = 6, Ker(Φ) ≤ ℤ₁₂, the only subgroup that fits the bill is Ker(Φ) = ⟨2⟩ = {0, 2, 4, 6, 8, 10}. |G/Ker(Φ)| = 2, so G/Ker(Φ) ≋ ℤ₂. Therefore, G is partitioned in two cosets H and 1 + H = {1, 3, 5, 7, 9, 11}. Φ carries the identity, Φ(0) = 0 ⇒[Φ(a) = Φ(b) ↭ aKer(Φ) = bKer(Φ).] We need to map H to zero, and 1 + H to 1 (e.g., 1 + H = 3 + H ↭ Φ(1) = Φ(3)).

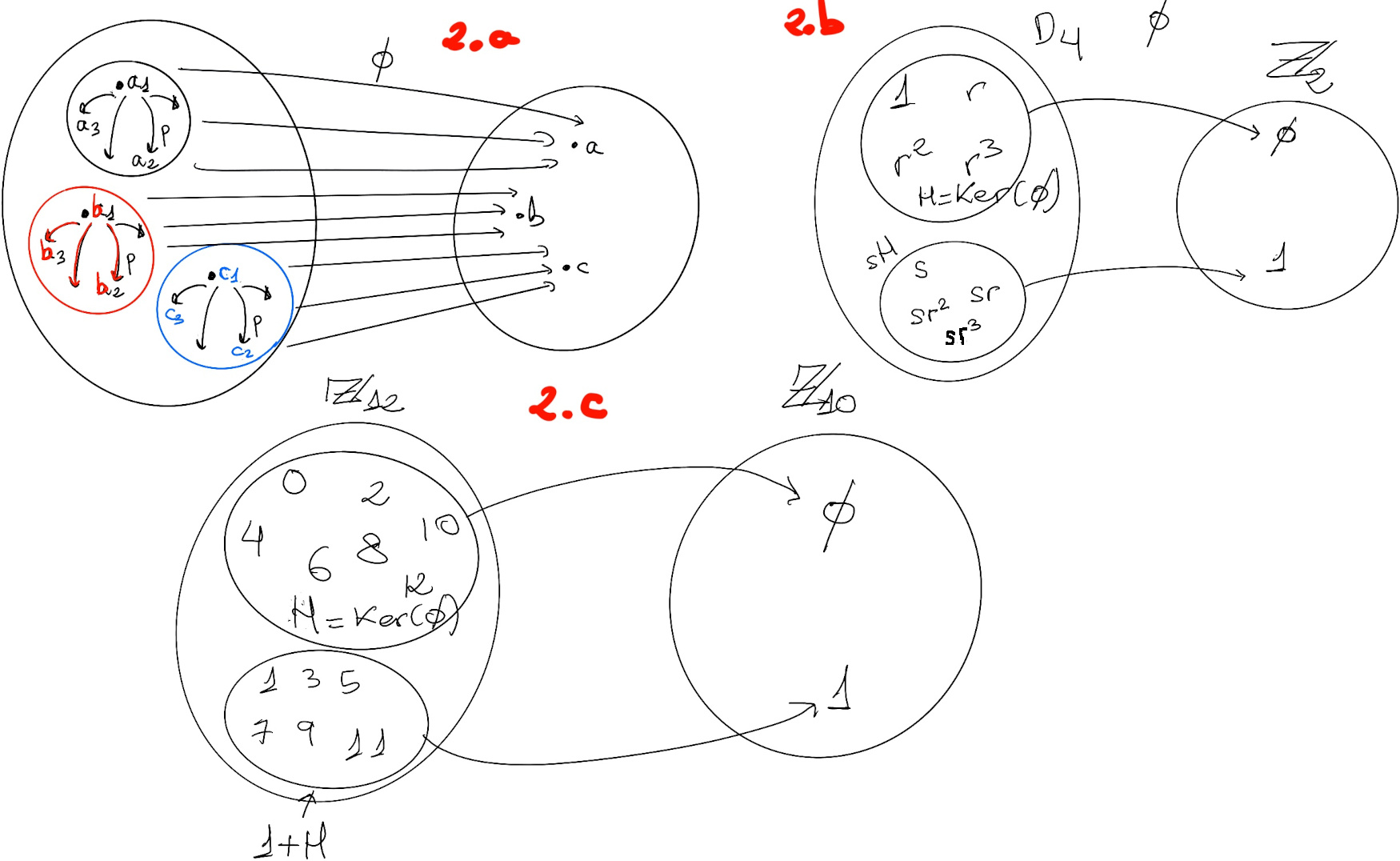
What are the group homomorphisms from D₄ to ℤ₂?

1. Ker(Φ) ≤ D₄ ⇒[By Lagrange’s Theorem] |Ker(Φ)| divides 8 ⇒ |Ker(Φ)| = 1, 2, 4 or 8.
2. First Isomorphism Theorem: D₄/Ker(Φ) ≋ Φ(D₄) and Φ(D₄) ≤ ℤ₂ ⇒[By Lagrange’s Theorem] |G/Ker(Φ)| = |G|/|Ker(Φ)| = 8/|Ker(Φ)| divides 2.
3. 1 & 2 ⇒ |Ker(Φ)| = 4 or 8.
4. If |Ker(Φ)| = 8 ⇒ G = Ker(Φ) and Φ is the trivial homomorphism.
5. If |Ker(Φ)| = 4, |G/Ker(Φ)| = 2, H = Ker(Φ) ≤ D₄.

There are three options (three groups of order 4 in D₄):
a) H = ⟨r⟩ = {1, r, r², r³}. sH = {s, sr, sr², sr³}, D₄ = H ∪ sH. Φ: D₄ → ℤ₂ and is determined by Φ(r) = 0 and Φ(s) = 1
b) H = ⟨s, r²⟩ = {1, s, r², sr²}, rH = {r, rs, r³, rsr²} =[r^ks = sr^4-k, 1 ≤ k ≤ 3, (rs)r² = sr³r² = sr⁵ = sr] {r, sr³, r³, sr}. Φ: D₄ → ℤ₂ and is determined by Φ(r) = 1 and Φ(s) = 0
c) H = ⟨sr, r²⟩ = {1, sr, r², sr³}, rH = {r, rsr, r³, rsr³} = [r^ks = sr^4-k, 1 ≤ k ≤ 3, (rs)r³ = sr³r³ = sr²; rsr = sr³r = s] {r, s, r³, sr²}. Φ: D₄ → ℤ₂ and is determined by Φ(r) = Φ(s) = 1. Notice that Φ(r²) = Φ(r) + Φ(r) = 1 +_{mod 2} 1 = 0 and Φ(sr) = Φ(s) + Φ(r) = 1 +_{mod 2} 1 = 0.

• The homomorphic image of an Abelian group is Abelian; that is, if H is Abelian, then Φ(H) is Abelian, too.

Proof. They have already been demonstrated in our article about isomorphisms because we have only used that isomorphisms are operation-preserving mappings.

• The homomorphic image of a normal group is normal in the image of G; that is, if H is normal in G (H ◁ G), then Φ(H) is normal in Φ(G) (Φ(H) ◁ Φ(G))

Proof.

Suppose H ◁ G. Claim: Φ(H) ◁ Φ(G)

∀g ∈ G, ∀h ∈ H, Φ(g)Φ(h)(Φ(g))^-1 =[Φ(aⁿ) = (Φ(a))ⁿ] Φ(g)Φ(h)Φ(g^-1) =[Φ homomorphism] Φ(ghg^-1) ∈ Φ(H) because H ◁ G.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.