Field Theory II

Recall

“Oh, money, the best deodorant, companion, motivator, and sex appeal. There are things far more important than money, but they all cost money and they won’t date you if you don’t have any cash,” Apocalypse, Anawim, #justtothepoint.

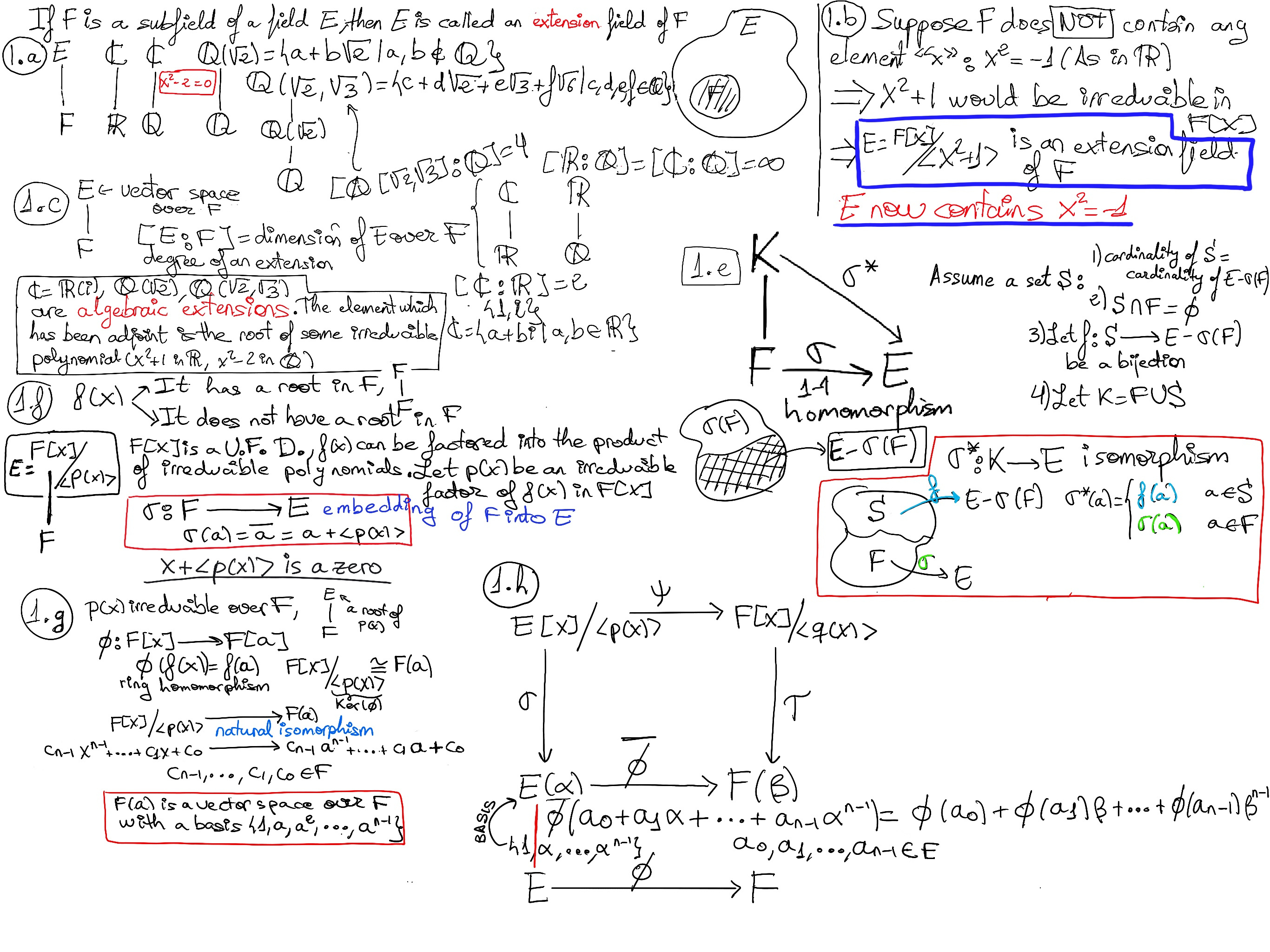
Theorem. Let E and F be two fields, and let σ: F → E be an embedding of a field F into a field E. Then there exist a field K such that F is a subfield of K and σ can be extended to an isomorphism of K onto E.

Krnoecker’s Theorem. Existence of extension. Let F be a field and let f(x) be a non-constant polynomial in F[x]. Then, there exists an extension E of F in which f(x) has a root or zero. (Figure 1.f)

Theorem. Let p(x) be an irreducible polynomial in F[x] and let u be a root of p(x) in an extension E of F. Then,

1. F(u), the subfield of E generated by F and u is the smallest field containing F and u. It is indeed F[u], the smallest subring containing both F and u = {b₀ + b₁u + ··· + b_mu^m ∈ E | b₀ + b₁x + ··· + b_mx^m ∈ F[x]}

2. If the degree of p(x) is n, the set (1, u, ···, u^n-1) forms a basis of F(u) over F, i.e., each element of F(u) can be written uniquely as c₀ + c₁u + ··· + c_nu^n-1 where c_i ∈ F, and [F(u):F] = n.

Definitions. An element α ∈ E is algebraic over F if there exists a non-constant polynomial p(x) ∈ F[x] such that p(α)=0, i.e., α is the root of p(x). Example: E = ℂ, F = ℚ, α = $\sqrt{2}$ is algebraic over ℚ, p(x) = x² -2, and p($\sqrt{2}$)=0. Similarly, i is algebraic over ℚ, p(x) = x² + 1, p(i) = 0. An element that is not algebraic, i.e., there no exists a non-constant polynomial p(x) such that p(α)=0 is called transcendental, e.g., π.

An extension E of F is called algebraic if each element of E is algebraic over F. An extension that is not algebraic, it is called transcendental, e.g, the extension ℝ over ℚ is a transcendental extension, and ℂ = ℝ(i) and ℚ($\sqrt{5}$) are algebraic extensions over ℝ and ℚ respectively (x² + 1, x² -5).

The minimal polynomial

The minimal polynomial of u over F is the monic (the leading coefficient is equal to 1) irreducible polynomial in F[x] of which u is a root.

Theorem. Let E be an extension field of F, and let u ∈ E be algebraic over F. Let p(x) ∈ F[x] be a polynomial of least degree such that p(u) = 0, we call p the minimal polynomial of u over E, Then,

(i) p(x) is irreducible over F
(ii) if g(x) ∈ F[x] is such that g(u) = 0, then p(x) | g(x)
(iii) There is exactly one monic polynomial p(x) ∈ F[x] of least degree such that p(u) = 0. This monic polynomial always exists because we can always divide the minimal polynomial by its leading coefficient, and still u be a root.

Proof.

(i) Let’s suppose for the sake of contradiction, that p(x) is reducible over F. Let p(x) = p₁(x)·p₂(x) such that deg(p₁(x)), deg(p₂(x)) < deg(p(x)).

We know that u is a root of p(x) ⇒ p(u) = 0 ⇒ p₁(u)·p₂(u) = 0 ⇒ p₁(u) = 0 or p₂(u) = 0, and deg(p₁(x)), deg(p₂(x)) < deg(p(x)), i.e., u satisfies a polynomial of degree less that p(x) ⊥ [By assumption, p(x)∈ F[x] is a polynomial of least degree such that p(u) = 0]. Therefore, p(x) is irreducible.

(ii) Let g(x) ∈ F[x] such that g(u) = 0. By the division algorithm, g(x) = p(x)q(x) + r(x) where r(x) = 0 or degree(r(x)) < deg(p(x)) ⇒

1. If r(x) = 0 ⇒ g(x) = p(x)q(x) ⇒ p(x) | g(x)∎
2. Otherwise, g(u) = p(u)q(u) + r(u) ⇒ By (ii) assumption, g(u) = 0, and p(u) = 0, so r(u) = 0, and deg(r(x)) < deg(p(x)) ⊥

(iii) Let’s assume by reduction to the absurd, that g(x) is another monic polynomial of least degree which g(u) = 0 ⇒ [By (ii)] g(x)| p(x). However, p(x)|g(x) just by interchanging the roles of p(x) and g(x) and using (ii) again, g(x)|p(x) ⇒ p = Φ·g, g = ψ·p ⇒ p = Φ·ψ·p [When we multiply polynomials, their degrees are added, deg(f·g) = deg(f) + deg(g)] deg(Φ·ψ) = 0 ⇒ Φ and ψ need to be constant ⇒ [Since both p(x) and g(x) are monic polynomials, that is, the leading coefficients are 1] p(x) = g(x) ∎

Theorem. If E is a finite extension of F, then E is an algebraic extension of F.

Proof. Let’s select an arbitrary element of E, say u ∈ E, and [E:F] = n. The set {1, u, ··· , u^n-1, uⁿ} is linearly dependent ⇒ there exists a₀, a₁, ···, a_n (not all zero) in F such that a₀ + a₁u + ··· a_nuⁿ = 0. Thus, we have found a polynomial f(x) = a₀ + a₁x + ··· a_nxⁿ ∈ F[x] such that u in E is a root. Then, u ∈ E is an algebraic element over F. Moreover, u ∈ E was selected completely as an arbitrary of E. Hence, E is an algebraic extension of F ∎

Proposition. If p(x) is the minimal polynomial of α over F and degree(p(x))= n. Then, [F(α):F] = n, and, in particular, it is finite, so by our previous result, F(α) is an algebraic extension. More formally, if E is an extension of F and α ∈ E is algebraic over F, then F(α) is an algebraic extension of F and deg(F(α):F)=deg(p(x)) where p is the minimal polynomial of α.

Proof.

Let p be the minimal polynomial of α over F, say p(x) = xⁿ + a_n-1x^n-1 + ··· +a₀ where a_i ∈ F.

We claim that the collection {α⁰=1, α, α², ···, α^n-1} is a basis for F(α).

• Lineal independence. Suppose β₀·1 + β₁α + ··· + β_n-1α^n-1 = 0, β_i∈ F. If β_i are not all zeros, consider the polynomial f = β₀ + β₁x + ··· + β_n-1x^n-1. Then, f(α)=0, f is a non-zero polynomial (f ∈ F[x]) of degree n-1 < n ⊥ (p is the minimal polynomial of α).

• Spans. F(α) = F[α] = {$\sum_{i=0}^m β_iα^i$| m ∈ ℕ, β_i ∈ F}. Obviously F[α] ⊆ F(α), since F[α] is the minimal subring containing F and α. Besides, F(α) ⊆ F[α] is obvious, too, just take all coefficients β_i to zero except β₁=1 to get α, and similarly you can get all elements of F. It is more complicated to show that F[α] is a field, that is, it is closed under all field operations.

• Finally, F(α) = F[α] = $\sum_{i=0}^m β_iα^i$| m ∈ ℕ, β_i ∈ F} =[💡{α⁰=1, α, α², ···, α^n-1} linear independence] $\sum_{i=0}^{n-1} β_iα^i$| β_i ∈ F}. Consider p = xⁿ + ax^n-1 + ··· +a₀. Then, 0 = αⁿ + a_n-1α^n-1 + ··· +a₀ ⇒ αⁿ = -a_n-1α^n-1 + ··· -a₀, so we can express αⁿ as a linear combination of {1, α, ···, α^n-1}, and we can apply the same idea with α^m, m > n, and therefore, F[α] = $\sum_{i=0}^m β_iα^i$| m ∈ ℕ, β_i ∈ F} = $\sum_{i=0}^{n-1} β_iα^i$| β_i ∈ F}.

Fact. Every finite extension is an algebraic extension, but the converse is not true, i.e., every algebraic extension is not a finite extension.

Example. E = ℚ($\sqrt{2},\sqrt{3},···,\sqrt{p}$) the smallest subfield of ℝ containing the rationals and all square root of positive primes is an algebraic extension but it is not a finite extension.

(i) E is an algebraic extension. Let α ∈ E ⇒ ∃r ∈ ℤ⁺ such that α ∈ ℚ($\sqrt{p_1},\sqrt{p_2},···,\sqrt{p_r}$). We know that ℚ($\sqrt{p_1},\sqrt{p_2},···,\sqrt{p_r}$) is a finite extension of degree 2^r ⇒ [Every finite extension is algebraic] α is algebraic over ℚ, and α was selected arbitrary, so E is an algebraic extension.

Notice that ℚ($\sqrt{2}$), its corresponding polynomial is x²-2 = 0, then the degree of the extension is 2. Analogously, ℚ($\sqrt{2}, \sqrt{3}, \sqrt{5}$) their corresponding polynomials are x² -2, x² -3, and x² + 5, so the degree of the extension is 2·2·2 = 6 = 2³.

(ii) E is an infinite extension. Claim: Each new adjunction of the square root of a prime is a proper extension, i.e. ℚ ⊂ ℚ($\sqrt{2}$) ⊂ ℚ($\sqrt{2}, \sqrt{3}$) ⊂ ···

Let F = ℚ($\sqrt{p_1},\sqrt{p_2},···, \sqrt{p_n}$) where p_i i=1, ··· n are distinct primes. Let’s show that ℚ($\sqrt{p_1},\sqrt{p_2},···, \sqrt{p_n}, \sqrt{q}$) is a proper extension of F, we must show that $\sqrt{q}$ ∉ F, and prove it by using induction on n.

1. If n = 0 ⇒ F = ℚ ⇒ $\sqrt{q}$, q prime is an irrational number and $\sqrt{q}$ ∉ F = ℚ
2. Let us assume that result is true for n-1.

Let F₀ = ℚ($\sqrt{p_1},\sqrt{p_2},···, \sqrt{p_{n-1}}$), F = F₀($\sqrt{p_n}$) is an extension F of F_o of degree 2 -a proper extension-, i.e. [F:F₀] = 2 because $\sqrt{p_n}$ is a root of x² -p_n ∈ F₀[x], and x² -p_n is irreducible in F_o[x].

We want to prove that $\sqrt{q}$ ∉ F = ℚ($\sqrt{p_1},\sqrt{p_2},···, \sqrt{p_{n}}$), so it is possible to create a proper extension ℚ($\sqrt{p_1},\sqrt{p_2},···, \sqrt{p_{n}}, \sqrt{q} $).

Let’s assume by reduction to the absurd that $\sqrt{q}$ ∈ F = F₀($\sqrt{p_n}$) ⇒ $\sqrt{q} = a·1 + b·\sqrt{p_n}$ where a, b ∈ F₀ ⇒ $q =a^2+b^2p_n+2ab\sqrt{p_n} ⇒ 0 = a^2+b^2p_n+2ab\sqrt{p_n}-q$ ⇒[This is a second equation ax²+ bx +c where the roles are a = b², b = 2ab, c = a²-q] $\sqrt{p_n}=\frac{-2ab±\sqrt{4a^2b^2-4(a^2-q)b^2}}{2b^2}=\frac{-2ab±2b\sqrt{q}}{2b^2}=\frac{-a}{b}±\frac{\sqrt{q}}{b}$ ∈[a, b ∈ F_o and by assumption, $\sqrt{q}$ ∈ F = F₀($\sqrt{p_n}$)] F₀, $\sqrt{p_n} ∈$ F₀ = ℚ($\sqrt{p_1},\sqrt{p_2},···, \sqrt{p_{n-1}}$) which is a contradiction because F = F₀($\sqrt{p_n}$) is a proper extension of F₀ ⇒ $\sqrt{q}$ ∉ F ⇒ ℚ ⊂ ℚ($\sqrt{2}$) ⊂ ℚ($\sqrt{2}, \sqrt{3}$) ⊂ ··· is an infinite properly ascending chain and E is not a finite extension of ℚ∎

Theorem. If f ∈ K[x] is monic, irreducible, (it cannot be written as a product of non constant polynomials)and f(α)= 0, then f is the minimal polynomial of α.

Proof. Suppose that f ∈ K[x] monic, irreducible, and f(α) = 0.

Suppose by reduction to the absurd, that f is not the minimal polynomial of f ↭ there is such a polynomial Φ, Φ|f ⇒ f = Φ·g ⇒ [By assumption, f is irreducible] g is constant, g ∈ K ⇒ [f is monic] g = 1 ⇒ f = Φ∎

Example. The number $\sqrt{2}$ has minimal polynomial x² -2 over ℚ, but x² -2 is not irreducible over ℝ. x² -2 is monic, f($\sqrt{2}$) = 0, and it is irreducible over ℚ, so it is the minimal polynomial of $\sqrt{2}$.

Suppose for the sake of contradiction, x²-2 is not irreducible over ℚ ↭ ∃a, b, c, d ∈ ℚ such that (ax + b)(cx +d) = x² - 2 ⇒ ac = 1, bc + ad = 0, and bd = -2 ⇒ ∃a, b, c, d ∈ ℚ such that b = ±$\sqrt{2}$a, a ≠ 0, c = 1/a, d = ±$\sqrt{2}$/a ⊥ ⇒ x² -2 is irreducible over ℚ

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.