Euclidean and Noetherian domain

“Are you Judith’s project leader?” “The one and only. Project leader, analyst, and programmer, three roles, lots of work, and one biological, carbon-based, bipedal emotional organism that turns roasted beans’ beverage into undocumented code -start praying for the next developer,” I replied, Apocalypse, Anawim, #justtothepoint.

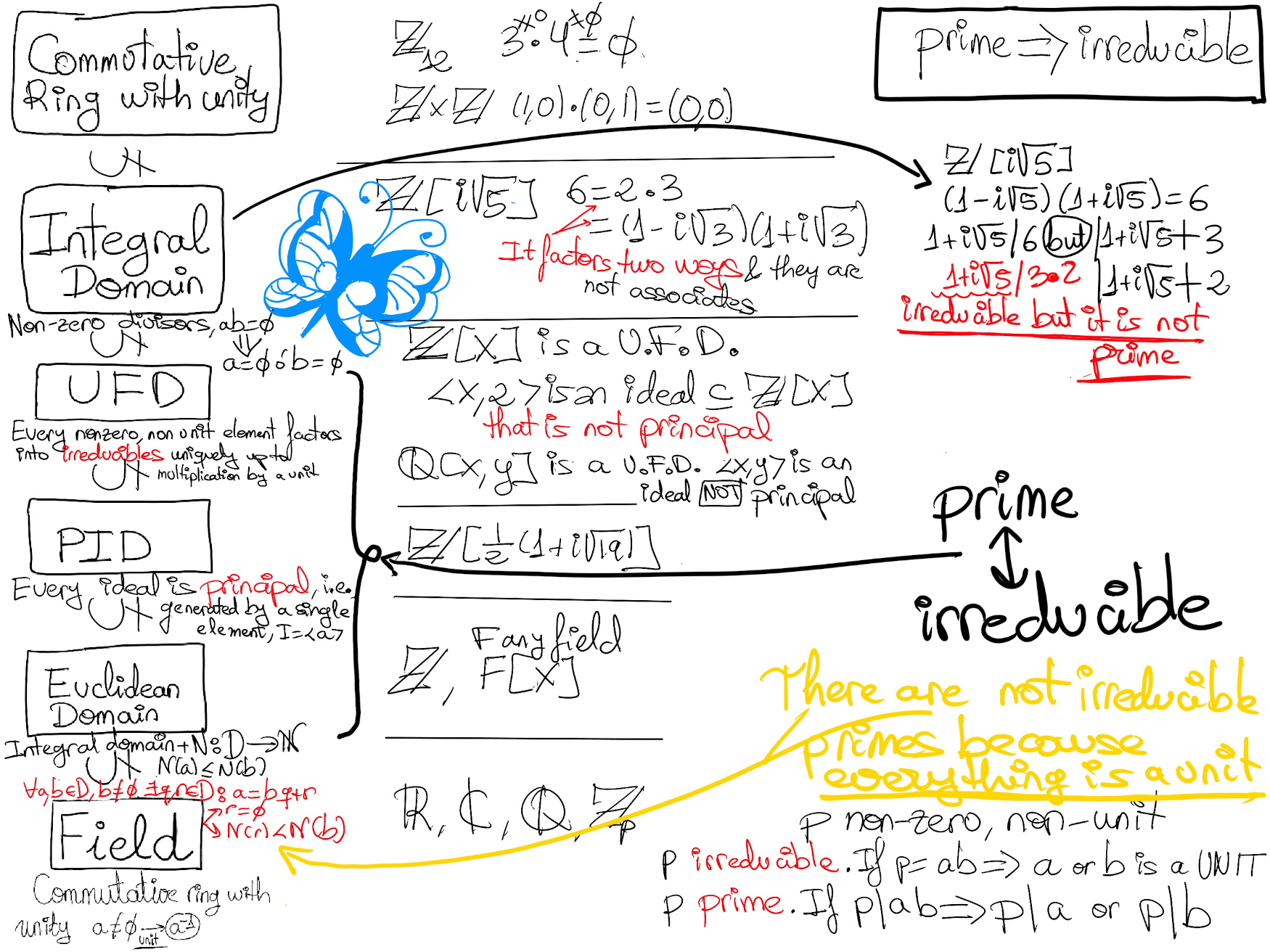
Recall. Let R be a commutative ring with unity and D an integral domain. An integral domain is a commutative ring with a multiplicative identity (1 ≠ 0) with no zero-divisors, that is, ab = 0 ⇒ a = 0 or b = 0.

A unique factorization domain is a ring in which a statement similar to the fundamental theorem of arithmetic holds. Specifically, a UFD is an integral domain in which every non-zero non-unit element can be written as a product of prime or irreducible elements uniquely up to order and multiplication by units. 💡In an integral domain every prime is irreducible.

Definition. We say an integral domain D is a unique factorization domain, UFD for short, if:

1. Every non-zero non-unit element of D can be factored, expressed or written as a product of irreducibles of D.
2. This factorization into irreducibles is unique in the following sense. If a = up₁p₂···p_m = wq₁q₂···q_n, u and w units, then m = n and there exists a bijective map Φ:{1, 2, …, n} → {1, 2, …, n} such that p_i is associated to q_Φ(i) ∀i ∈ {1, 2, …, n}. In other words, ∃Φ ∈ S_n: p_i = q_Φ(i)u_i and u_i is a unit ∀i ∈ {1, 2, …, n}.

Definition. A ring R is said to satisfy the ascending chain condition, ACC for short, if for every set of ideals {I_j} such that I₁ ⊆ I₂ ⊆ I₃ ⊆ ··· there exists N ∈ ℕ such that I_n = I_N for all n ≥ N. In other words, any strictly increasing chain of ideals must be finite.

Definition. A Noetherian domain is an integral domain satisfying the ascending chain condition, that is, any strictly increasing chain of ideals must be finite or, in other words, every ascending or increasing chain of ideals eventually stabilizes.

Lemma. Every principal ideal domain satisfies the ascending chain condition.

Proof.

Suppose D is a PID and {I_j} is a set of ideal such that I₁ ⊆ I₂ ⊆ I₃ ⊆ ··· . Let I = $\cup_{j=1}^{∞}I_j$. We claim that this is an ideal.

1. It is a subring. Suppose a, b ∈ I. Let’s use the subring test to prove that it is a subring. ∃l, k ∈ ℕ: a ∈ I_l and b ∈ I_k ⇒ a, b ∈ I_{max{l, k}} ⇒ [I_{max{l, k}} is an ideal and therefore a subring] b - a, ab ∈ I_{max{l, k}} ⊆ I.
2. It is an ideal. Suppose a ∈ I, r ∈ D ⇒ ∃k ∈ ℕ: a ∈ I_k ⇒ [I_k is an ideal] ra ∈ I_k ⊆ I.
3. Truncation. We know that I ideal in a PID ⇒ [Every ideal is generated by a single element] ∃a ∈ D: I = ⟨a⟩ ⇒ In particular, a ∈ I = $\cup_{j=1}^{∞}I_j$ ⇒ ∃N ∈ ℕ: a ∈ I_N ⇒ ⟨a⟩ ⊆ I_N ⇒ I = ⟨a⟩ ⊆ I_N ⊆ I_N+1 ⊆ I_N+2··· ⊆ I = ⟨a⟩ ⇒ I_n = I_N for all n ≥ N ∎

Theorem. Every principal ideal domain, PID for short, is a unique factorization domain, UFD.

Proof.

Let’s prove factorization. Suppose a ∈ D that is a non-zero non-unit element. We will show that a is a product of irreducibles. We start by showing that a has at least one irreducible factor, that is a could be the product of only one irreducible factor.

Obviously, if a is irreducible, then we are done ∎

Recall. A non zero, non unit element a of an integral domain D is irreducible if when a = bc, then b or c is a unit. In other words, it cannot be written as a non trivial (except units) product of two elements of the ring.

Thus, we may assume that a = a₁b₁ where neither a₁ or b₁ are units, and a₁ is nonzero. If a₁ is not irreducible, then a₁ can be expressed as a product a₁ = a₂b₂ where neither a₂ nor b₂ is a unit and a₂ is nonzero. And so on, and so forth…(Continuing with this process, we can construct an infinite ascending chain of ideals) a_k = a_k+1b_k+1 ⇒ a₁|a, a₂|a₁, ···, a_k+1|a_k ⇒ [a|b ↭ ⟨b⟩ ⊆ ⟨a⟩] ⟨a⟩ ⊂ ⟨a₁⟩ ⊂ ⟨a₂⟩··· ⊂ ⟨a_k⟩··· ⇒ [D satisfies the ACC, this sequence stabilizes] ∃N ∈ ℕ: ⟨a_N⟩ = ⟨a_N+1⟩ = ⟨a_N+2⟩ = ··· ⇒ ⟨a⟩ ⊆ ⟨a₁⟩ ⊆ ⟨a₂⟩··· ⊆ ⟨a_N⟩ = ⟨a_N+1⟩ = ⟨a_N+2⟩ = ··· ⇒ ∀n ≥ N, ⟨a_N⟩ = ⟨a_n⟩ ⇒ [a and b are associates -one can be obtained from the other by multiplying by some unit, a = bu, u unit- ↭ ⟨b⟩ = ⟨a⟩] a_N and a_n are associates ∀n ≥ N ⇒ a = a₁b₁ = a₂(b₁b₂) = ··· = a_N(b₁b₂···b_N-1) where a_N is an irreducible factor of a (we will rename it as p₁). We have already proved that every non-zero non-unit element in D has at least one irreducible factor.

Therefore, given a non-zero, non-unit element a ∈ D ⇒ a = p₁x₁, p₁ irreducible and x₁ is not a unit. If x₁ is not irreducible, then we can write x₁ = p₂x₂, where p₂ is irreducible and x₂ is not a unit. We continue this argument and we can obtain as before x_k = p_k+1x_k+1, where p_k+1 is irreducible ⇒ Therefore, there’s an infinite ascending chain of ideals ⟨x₁⟩ ⊂ ⟨x₂⟩··· ⊂ ⟨x_k⟩··· ⇒ By the same argument as before, there exists r such that ∀n≥r: ⟨x_n⟩ = ⟨x_r⟩, that is, x_r is an irreducible factor, and a = p₁x₁ = p₁p₂x₂ = ··· = p₁p₂···p_rx_r where x_r and p_i, ∀i such that 1 ≤ i ≤ r are all irreducibles. Therefore, a has a prime factorization.

Let’s prove that the factorization is unique up to associates and the order in which all these factors appear.

Let’s suppose that an arbitrary element a ∈ D can be factored or written as two products of irreductibles, say a = p₁p₂···p_r = q₁q₂···q_s where the p_i and q_j are irreducible and we are going to demonstrate the uniqueness by induction on r.

Without loss of generalization, we could assume that r ≤ s.

• Case base: If r = 1 ⇒ a = p₁ is irreducible, and obviously s = 1, and p₁ = q₁ and we are done.
• Hypothesis induction. Our induction hypothesis is that any elements that can be expressed as a product of fewer than r irreducible factors can be so expressed uniquely in only such a way, up to order and associates.
• Let’s suppose r > 2. a = p₁p₂···p_r = q₁q₂···q_s. We know that p₁ | a, p₁ is prime (We have already shown that in a principal ideal domain, irreducible elements are prime elements) ⇒[p₁ | q₁q₂···q_s] p₁|q_j for some j. By rearrangement or renaming, we may assume that q_j = q₁

As p₁|q₁, and they are both irreducibles, then u₁p₁ = q₁ where u₁ is a unit of D, then u₁p₁p₂···p_r = u₁q₁q₂···q_s =[Commutative ring] q₁(u₁q₂)···q_s ⇒ [u₁p₁=q₁, PID has cancellation laws] p₂···p_r = (u₁q₂)···q_s

The induction hypothesis tells us that these two factorization are identical up to associates and the order in which the factor appear. Therefore r = s and there is a one-to-one correspondence between the irreducibles of these prime factorizations or in other words, this factorization is identical up to associates and the order in which the factors appear.

Corollary. Let F be a field. Then, F[x] is a unique factorization domain.

Proof. If F is field ⇒ F[x] is a principal ideal domain ⇒[Theorem. Every principal ideal domain, PID for short, is a unique factorization domain, UFD.] F[x] is a unique factorization domain.

Definition. An integral domain is known as a Euclidean domain if there is a mapping or function N (called the measure or the Euclidean function) from the nonzero elements of D to the natural numbers such that

1. If a,b ∈ D, a ≠ 0, b ≠ 0, then N(a) ≤ N(ab)
2. If a, b ∈D, b ≠ 0, then ∃q, r ∈D such that a = bq + r, where r = 0 or N(r) < N(b).

It is an integral domain that can be endowed with a Euclidean function which allows a suitable generalization of the Euclidean division of integers, ∀a, b ∈ ℤ, b ≠ 0, ∃!q, r ∈ ℤ: a = bq + r, 0 ≤ r < |b|.

Examples

1. Any field, N(m) = 1 ∀m ∈ F, m ≠ 0.
2. ℤ is a Euclidean domain, N(m) = |m|.
3. Let F be a field, F[x] is a Euclidean domain with N(f(x)) = deg(f(x)).

   ∀f(x), g(x) ∈ F[x], g(x) ≠ 0, deg(f(x)·g(x)) = deg(f(x)) + deg(g(x))≥ deg(g(x)). ∀f(x), g(x) ∈ F[x], f(x) ≠ 0, g(x) ≠ 0, ∃q(x), r(x)∈ F[x]: f(x) = g(x)q(x) + r(x), r(x) = 0 or 0 ≤ deg(r(x)) < deg(g(x)).

4. The ring of Gaussian integers, Z[i]={a + bi| a, b ∈ ℤ} is a Euclidean domain, where N(α) = $α\bar{α}=|α|^2$. Notice that α = a + bi ⇒ $\bar{α}=a - bi$ ⇒ N(α) = a² + b².

• α, β ∈ Z[i] ⇒ αβ = $αβ\overline{αβ}=αβ\bar{α}\bar{β}=α\bar{α}β\bar{β}$ = N(α)N(β) [N(β) ≥ 1 if β ≠ 0, β ∈ ℤ] ≥ N(α)

• α, β ∈ Z[i], β ≠ 0 ⇒ β is invertible in the complex numbers. α = a + bi, β = c + di, β^-1 = $\frac{c-di}{c^2+d^2}=\frac{\bar{β}}{|β|^2}$

αβ^-1 = $\frac{(a+bi)(c-di)}{c^2+d^2}=\frac{1}{c^2+d^2}((ac+bd)+(bc-ad)i)=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i=(q_1+r_1)+(q_2+r_2)i,~ where \frac{-1}{2}≤r_1,r_2≤\frac{1}{2}$ where q₁, q₂ ∈ ℤ.

Recall that the ceiling is defined as the smallest integer that is larger or equal to x. The floor is defined as the largest integer that is smaller or equal to x, so x is between the floor of x, ⌊x⌋ and the ceiling of x, ⌈x⌉. Therefore, there are always two options, x = ⌊x⌋ + r₁, 0 ≤ r₁ ≤ 1/2 or x = ⌈x⌉ + r₁, -1/2 ≤ r₁ ≤ 0. In other words, ∀x ∈ ℤ, ∃x' ∈ ℤ: x = x' + r, $\frac{-1}{2}≤r≤\frac{1}{2}$

αβ^-1 = (q₁ + q₂i) + (r₁ + r₂i), let us rename q₁ + q₂i = γ ∈ ℤ[i]. Then, αβ^-1 = γ + (r₁ + r₂i) ⇒ α = βγ + β(r₁ + r₂i) ⇒ [α and -β, γ ∈ ℤ[i]- βγ ∈ ℤ[i]] β(r₁ + r₂i) ∈ ℤ[i], let’s rename it as ρ, so α = βγ + ρ

N(ρ) =[ρ = β(r₁ + r₂i)] $β\bar{β}(r_1+r_2i)(r_1-r_2i)=N(β)(r_1^2+r_2^2)~ where \frac{-1}{2}≤r_1,r_2≤\frac{1}{2}⇒~0≤r_1^2,r_2^2≤\frac{1}{4}⇒ N(ρ) ≤ \frac{N(β)}{2} < N(β)$. Therefore, ∀α, β ∈ Z[i], β ≠ 0, ∃γ, ρ ∈ Z[i] such that α = βγ + ρ and N(ρ) < N(β) ∎

Exercise. The ring of integers $ℤ[\sqrt{2}]$ = {$a +b\sqrt{2} | a, b ∈ ℤ$} is an Euclidean Domain.

First, it is an integral domain since it is contained in ℝ.

Then, let’s define the map $ℤ[\sqrt{2}]$ → ℕ, ∀a +b$\sqrt{2},N(a +b\sqrt{2})=|a +b\sqrt{2}||a -b\sqrt{2}| =|a^2-2b^2|$

$N(a +b\sqrt{2})N(c +d\sqrt{2})=|(a +b\sqrt{2})(a -b\sqrt{2})||(c +d\sqrt{2})(c -d\sqrt{2})| = |(a +b\sqrt{2})(a -b\sqrt{2})(c +d\sqrt{2})(c -d\sqrt{2})| = |(a +b\sqrt{2})(c +d\sqrt{2})||(a -b\sqrt{2})(c -d\sqrt{2})| = |(ac + 2bd)+(ad + bc)\sqrt{2}||ac + 2bd −(ad+bc)\sqrt{2}| = N(ac+2bd+(ad+bc)\sqrt{2}) = N((a+b\sqrt{2})(c+d\sqrt{2}))$. As a consequence, if $β≠0 ⇒ N(αβ) = N(a +b\sqrt{2})N(c +d\sqrt{2}) = N(α)N(β) ≥[β ≠ 0 ⇒ N(β)>0]~ N(α)$

Let’s α, β ∈ $ℤ[\sqrt{2}], α = a +b\sqrt{2}, β = c +d\sqrt{2}$ where a, b, c, d ∈ ℤ.

αβ^-1 = $\frac{a +b\sqrt{2}}{c +d\sqrt{2}}=\frac{a +b\sqrt{2}}{c +d\sqrt{2}}\frac{c -d\sqrt{2}}{c -d\sqrt{2}} = \frac{(ac-2bd)+(bc-ad)\sqrt{2}}{c^2-2d^2} = c_1 + c_2\sqrt{2},~ where~ c_1 = \frac{ac-2bd}{c^2-2d^2}, c_2 = \frac{bc-ad}{c^2-2d^2}$.

Let q₁ and q₂ be the closest integers to c₁ and c₂ respectively, that is, |c₁ -q₁| ≤ ¹⁄₂ and |c₂ -q₂| ≤ ¹⁄₂. Now, let γ = q₁ + q₂$\sqrt{2} ∈ ℤ[\sqrt{2}], θ = (c_1 -q_1) + (c_2 -q_2)\sqrt{2}, θ = \frac{α}{β}-γ$ ⇒ θβ = α -γβ ∈ ℤ[$\sqrt{2}$] because α, (β, γ∈ ℤ[$\sqrt{2}$] ⇒) γβ ∈ ℤ[$\sqrt{2}$]. Set δ = θβ, we have α = γβ + δ. Claim: N(δ)< N(β).

N(θ) =[Recall that $θ = (c_1 -q_1) + (c_2 -q_2)\sqrt{2}$] |$(c_1-q_1)^2-2(c_2-q_2)^2| ≤ |(c_1-q_1)^2| + |-2(c_2-q_2)^2| = (c_1-q_1)^2 + 2(c_2-q_2)^2 ≤ (\frac{1}{2})^2+2(\frac{1}{2})^2 = \frac{3}{4}$. In particular, N(δ) = N(θβ) = N(θ)N(β) ≤ ³⁄₄N(β), that is, N(δ) < N(β).

Theorem. If D is a Euclidean Domain, then it is a principal ideal domain.

Proof.

Suppose I ⊆ D is an ideal. We claim that I is principal, i.e., ∃b ∈ D such that I = ⟨b⟩.

Let b an element of I such that N(b) is minimal amongst all elements from I. We immediately have ⟨b⟩ ⊆ I.

I ⊆ ⟨b⟩? Let a be an arbitrary element of our ideal I, a ∈ I, a ∈ ⟨b⟩? ⇒ [D is a Euclidean Domain] ∃q, r ∈D: a = bq + r with r = 0 or N(r) < N(b). There are “two” options:

1. r = 0 ⇒ a = bq ⇒ a ∈ ⟨b⟩
2. r = a - bq ⇒ [a, bq ∈ I] r ∈ I, N(r) < N(b), and by assumption b is an element of I such that N(b) is minimal amongst all elements from I ⇒ r = 0 ⇒ a = bq ⇒ a ∈ ⟨b⟩. Therefore, I = ⟨b⟩.

Corollary. If D is a Euclidean domain, then it is a unique factorization domain.

Proof. ED ⇒[Previous Theorem. If D is a Euclidean Domain, then it is a principal ideal domain.] PID ⇒[Theorem. Every principal ideal domain, PID for short, is a unique factorization domain, UFD.] UFD.

• For the ring ℤ[$\sqrt{d}$] = {a + b$\sqrt{d}$| a, b ∈ ℤ}, where d ≠ 1 and d is not divisible by the square of a prime, prove that the norm N(a + b$\sqrt{d}$) = |a²-db²| satisfies the following assertions:

1. It is never zero. Recall that N is a mapping from the nonzero elements of D to the natural numbers. |a²-db²| = 0 ⇒ a² = db² ⇒[d ≠ 1 and d is not divisible by the square of a prime] a = 0 = b.
2. It is multiplicative: $N((a + b\sqrt{d})(a’ + b’\sqrt{d})) = N(aa’ +dbb’ + (ab’ + a’b)\sqrt{d}) = |(aa’ +dbb’)^2 -d(ab’ + a’b)^2| = |a^2a’^2 + d^2b^2b’^2 +2aa’dbb’ -da^2b’^2 -da’^2b^2 -2dab’a’b| = |a^2a’^2 + d^2b^2b’^2 -da^2b’^2 -da’^2b^2| = |a^2(a’^2-db’^2)-db^2(a’^2-db’^2)| = |(a^2-db^2)(a’^2-db’^2)| = |(a^2-db^2)||(a’^2-db’^2)| = N(a + b\sqrt{d})N(a’ + b’\sqrt{d})$
3. x is a unit ↭ N(x) = 1. Suppose x is a unit ⇒ ∃y: x·y = 1 ⇒ 1 = N(1) = N(xy) = N(x)N(y) ⇒ N(x) = N(y) = 1. Conversely, suppose x = a +b$\sqrt{d}$ such that |a²-db²| = N(x) = 1, choosing y = a -b$\sqrt{d}, xy = (a +b\sqrt{d})(a -b\sqrt{d}) = a^2 -db^2 =$[By assumption, |a²-db²| = N(x) = 1] ±1, and therefore, x = a +b$\sqrt{d}$ is a unit.
4. If N(x) is prime, then x is irreducible in ℤ[$\sqrt{d}$]. Suppose N(x) = N(a + b$\sqrt{d}$) = p, p prime. For the sake of contradiction, let’s suppose x is reducible ⇒ ∃y, z: x = yz where y and z are not units. p = N(x) = N(yz) = N(y)N(z) where N(y) ≠ 1 and N(z) ≠ 1 because z and y are not units in ℕ ⊥

• The ring R = ℤ[$\sqrt{-5}$] is an integral domain, but is not an Euclidean domain. Let N(a + b$\sqrt{-5}$) = a² +5b². Consider the ideal I = ⟨3, 2 + $\sqrt{-5}$⟩.

Suppose for the sake of contradiction ℤ[$\sqrt{-5}$] is a PID (Principal Ideal domain), then I is generated by an element, say I = ⟨a+b$\sqrt{-5}⟩ ⇒ (i)~ 3 = α(a+b\sqrt{-5}),(ii)~ 2 + \sqrt{-5} =β(a+b\sqrt{-5})$ for some α, β ∈ R

It was previously demonstrated that N(xy) = N(x)N(y) and N(x) = 1 ↭ x = ± 1 because -5 ≠ 1 and -5 is not divisible by the square of a prime.

(i) $3 = α(a+b\sqrt{-5}) ⇒ N(3) = 9 = N(α)(a^2+5b^2)$ ⇒[$a^2+5b^2$ is a natural] $a^2+5b^2$ = 1, 3 or 9. Therefore, there are three options:

1. $a^2+5b^2 = 9 ⇒ N(α) = 1 ⇒ α = ±1$ ⇒[(i)$3 = α(a+b\sqrt{-5})$] $a+b\sqrt{-5}=±3$ ⊥ By the second equation (ii), $2+\sqrt{-5} = β(±3)$ which is not possible because the coefficients of $2+\sqrt{-5}$ are not divisible by 3 in R.
2. $a^2+5b^2 = 3$ ⊥ there are no integer solutions to this equation.
3. $a^2+5b^2 = 1$ ⇒ 1 ∈ I ⇒ $1 = 3γ + (2+\sqrt{-5})δ$ ⇒[Multiplying both sides by $(2-\sqrt{-5})$] $(2-\sqrt{-5}) = 3(2-\sqrt{-5})γ + (4+5)δ) ⇒ (2-\sqrt{-5}) = 3((2-\sqrt{-5})γ +3δ) ⇒ (2-\sqrt{-5})$ is a multiple of 3 in R ⊥

Therefore, ℤ[$\sqrt{-5}$] is not a PID (Principal Ideal domain) ⇒[Previous Theorem. If D is a Euclidean Domain, then it is a principal ideal domain.] it is not an Euclidean Domain.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.