Determining volumes III

The man who asks a question is a fool for a minute, the man who does not ask is a fool for life, Confucius

Recall

Antiderivatives are fundamental concepts in calculus. They are the inverse operation of derivatives.

Given a function f(x), an antiderivative, also known as indefinite integral, F, is the function that can be differentiated to obtain the original function, that is, F’ = f, e.g., 3x² -1 is the antiderivative of x³ -x +7 because $\frac{d}{dx} (x^3-x+7) = 3x^2 -1$. Symbolically, we write F(x) = $\int f(x)dx$.

The process of finding antiderivatives is called integration.

The Fundamental Theorem of Calculus states roughly that the integral of a function f over an interval is equal to the change of any antiderivate F (F'(x) = f(x)) between the ends of the interval, i.e., $\int_{a}^{b} f(x)dx = F(b)-F(a)=F(x) \bigg|_{a}^{b}$

Calculating volumes with integrals is tricky and involves a variety of techniques such as slicing, the shell method, and the washer method.

Solved exercises

• The witch’s cauldron (I know, scary, ha ha ha!). Calculate the volume generated by the curve y = x² when is revolved around the y axis and bounded by y = a.

To calculate the volume generated by revolving the curve y = x² around the y-axis, we can use the method of cylindrical shells. The formula for finding the volume of revolution using cylindrical shells is: V = $2π\int_{a}^{b} x·f(x)dx$

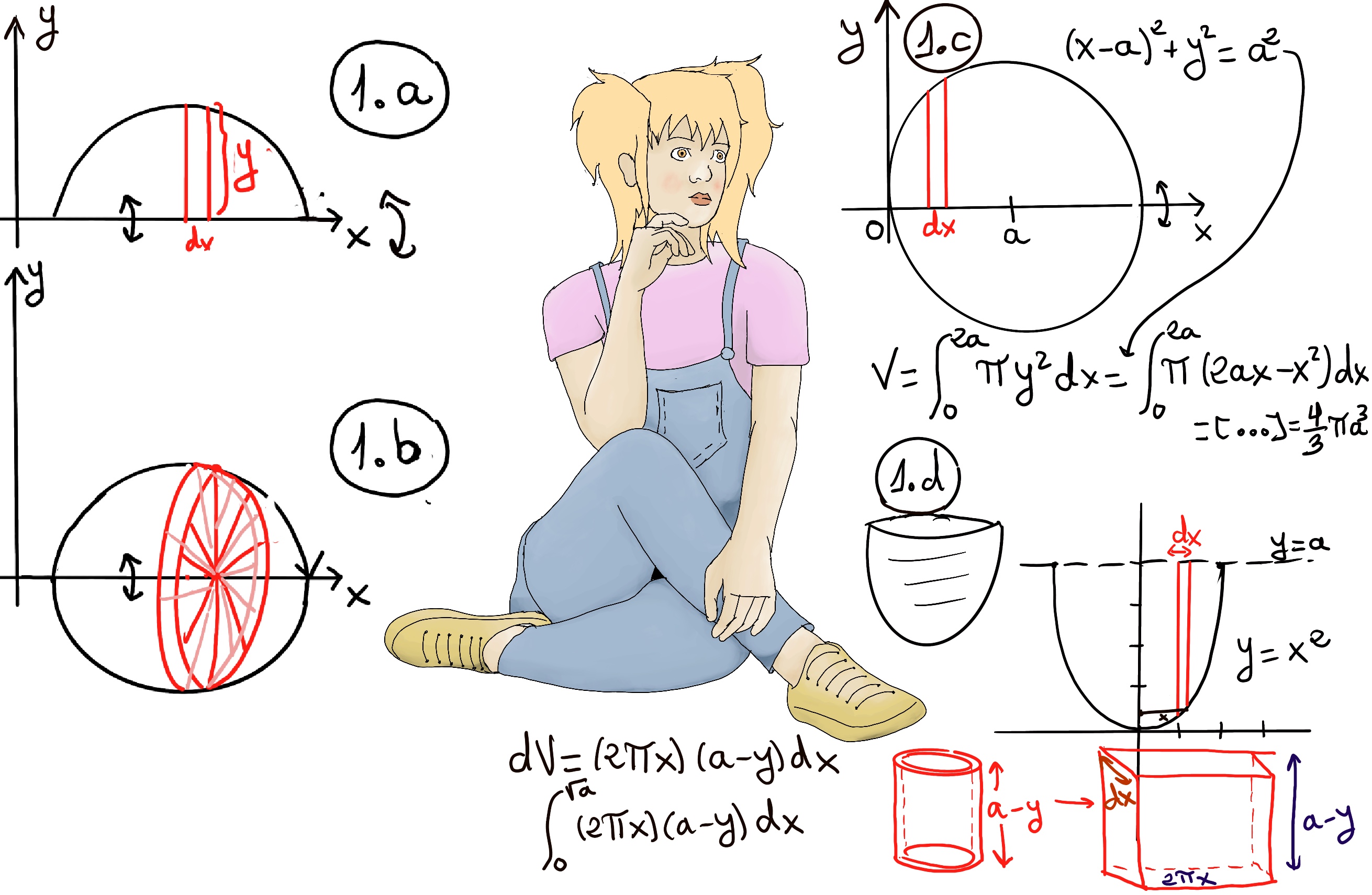
Let’s calculate the volumen of each shell. Thickness = dx, height = a -y (where y = x²), base = 2πx, dV = (2πx)(a -y)dx = (2πx)(a -x²)dx = 2π(ax -x³), V =[y = a, y = x² ⇒ x = √a] $\int_{0}^{\sqrt{a}} 2π(ax -x^3)dx = 2π(\frac{ax^2}{2}-\frac{x^4}{4})\bigg|_{0}^{\sqrt{a}} = 2π(\frac{a^2}{2}-\frac{a^2}{4}) = 2π\frac{a^2}{4} = \frac{π}{2}a^2$ -Figure 1.d.-.

• Find the volume of the solid of revolution bounded by the graphs of f(x) = $\sqrt{x}$, x = 1 and x = 4, and rotated about the x-axis (Figure B).

The solid of revolution is formed by revolving the region around the x-axis ⇒ the cross-sections are circles, A(x) = πr² where r = f(x) = $\sqrt{x}$, and the volume is $\int_{1}^{4} πr^2dx = \int_{1}^{4} πxdx = π\frac{x^2}{2}\bigg|_{1}^{4} = π(\frac{16}{2}-\frac{1}{2}) = \frac{15π}{2}$.

• Find the volume of the solid whose base is bounded by the curves y = x^2 and y = 2 -x^2 and whose cross sections through the solid perpendicular to the x-axis are squares (Figure C).

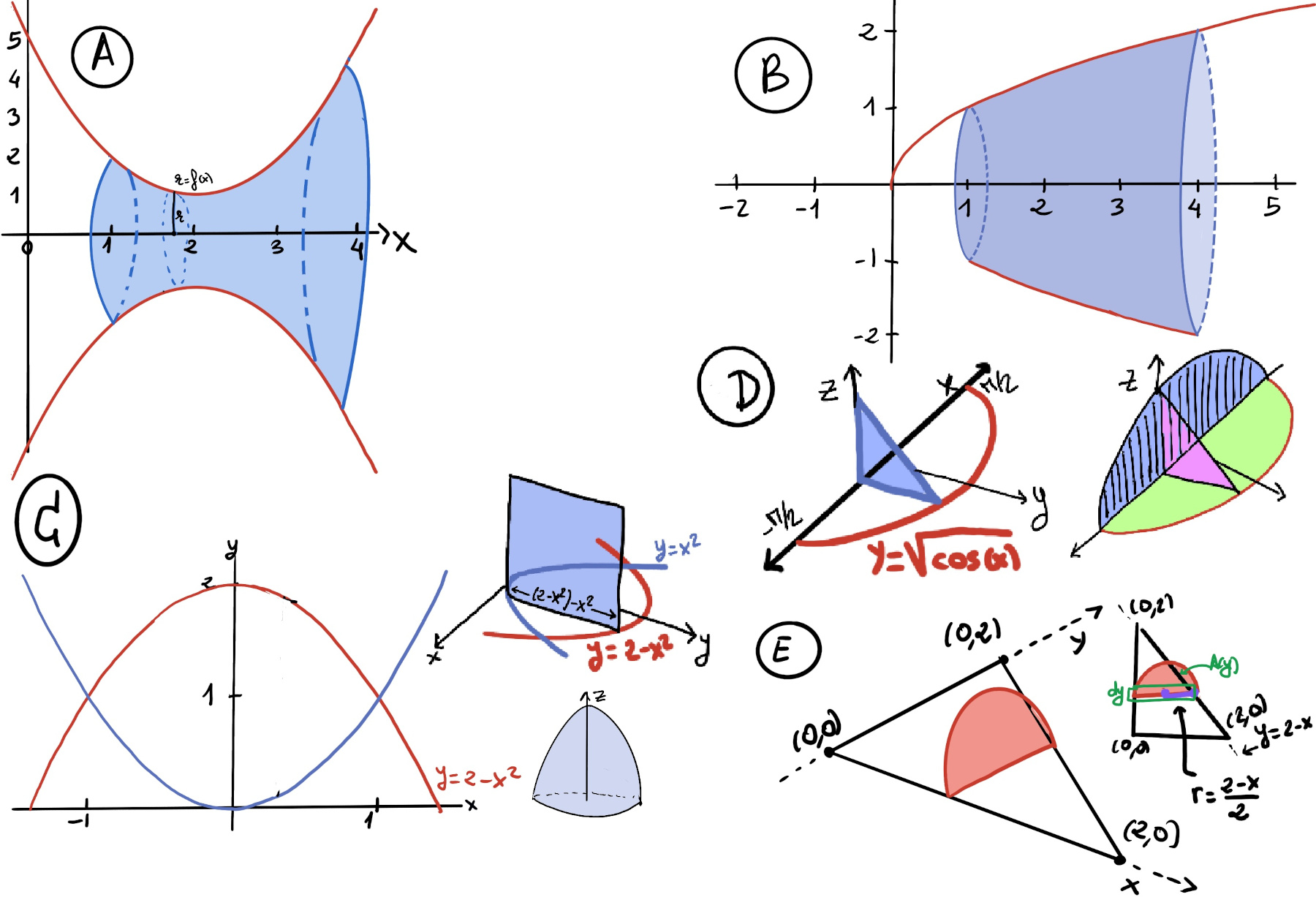
Let’s calculate the points of intersections: $x^2 = 2 -x^2 ↭ 2(x^2-1) =0$ ↭ x = ±1.

V = $\int_{-1}^{1} A(x)dx$ =[By symmetry] 2$\int_{0}^{1} A(x)dx$ =[Each cross section is a square with side of length (2-x²)-x²] $2\int_{0}^{1} ((2-x^2)-x^2)^2dx = 2\int_{0}^{1} (2-2x^2)^2dx = 2\int_{0}^{1} (4 -8x^2 + 4x^4dx) = 2(4x-\frac{8}{3}x^3+\frac{4}{5}x^5)\bigg|_{0}^{1} = 2(4-\frac{8}{3}+\frac{4}{5}) = 2(\frac{60}{15}-\frac{40}{15}+\frac{12}{15}) = 2·\frac{32}{15} = \frac{64}{15}.$

• Calculate the volume of the solid whose base is the region bounded by the curve y = $\sqrt{cos(x)}$ and the x-axis on [$\frac{-π}{2},\frac{π}{2}$], and whose cross sections through the solid perpendicular to the x-axis are isosceles right triangles with a horizontal leg in the xy-plane and a vertical leg above the x-axis, that is, the z-axis (Figure D)

We use the general slicing method to find the volume, V = $\int_{a}^{b} f(x)dx = \int_{\frac{-π}{2}}^{\frac{π}{2}} A(x)dx$[By symmetry] $2\int_{0}^{\frac{π}{2}} A(x)dx$ = [An isosceles right triangle is defined as a triangle with two equal sides known as the legs, a right angle, and two acute angles, A(x) = $\frac{1}{2}·\sqrt{cos(x)}·\sqrt{cos(x)}$] = $2\int_{0}^{\frac{π}{2}} \frac{1}{2}·(\sqrt{cos(x)})^2dx = \int_{0}^{\frac{π}{2}} cos(x)dx = sin(x)\bigg|_{0}^{\frac{π}{2}} = sin(\frac{π}{2})-sin(0) = 1.$

• Find the volume of the solid generated when the region bounded by $y = e^{\frac{x}{2}}, y = e^{-\frac{x}{2}}, x = ln(2), x = ln(3)$ is revolved about the x-axis (Figure 5).

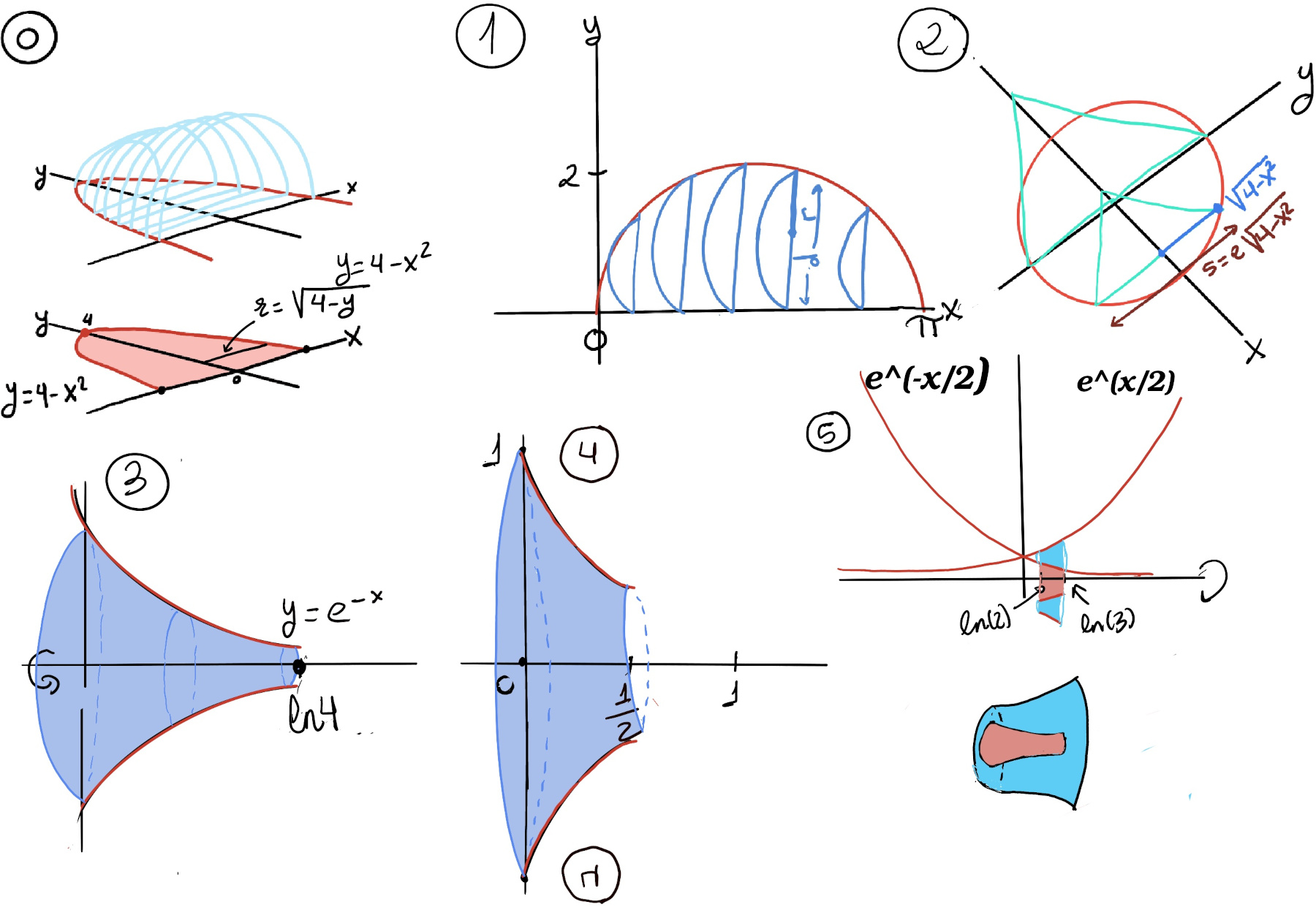
We have to use the washer method to find the volume of the solid formed by rotating two functions about an axis. The limits are logarithmic and are given in the question. We use the following formula: V = π·$\int_{a}^{b} (y_1^2-y_2^2)dx$

V = $\int_{ln(2)}^{ln(3)} π((e^{\frac{x}{2}})^2-(e^{\frac{x}{2}})^2)dx = π\int_{ln(2)}^{ln(3)} (e^x-e^{-x})dx = π(e^x+e^{-x})\bigg|_{ln(2)}^{ln(3)} = π(e^{ln(3)}+e^{-ln(3)}-(e^{ln(2)}+e^{-ln(2)})) = π(e^{ln(3)}+e^{ln(3)^{-1}}-(e^{ln(2)}+e^{ln(2)^{-1}})) = π(3+\frac{1}{3}-(2+\frac{1}{2}))=π(1+\frac{2}{6}-\frac{3}{6}) = π(1-\frac{1}{6}) = \frac{5}{6}π$

• Find the volume of the solid generated when the region bounded by y = x²+1, y = -x+1, and x = 1 is revolved about the y-axis (Figure α)

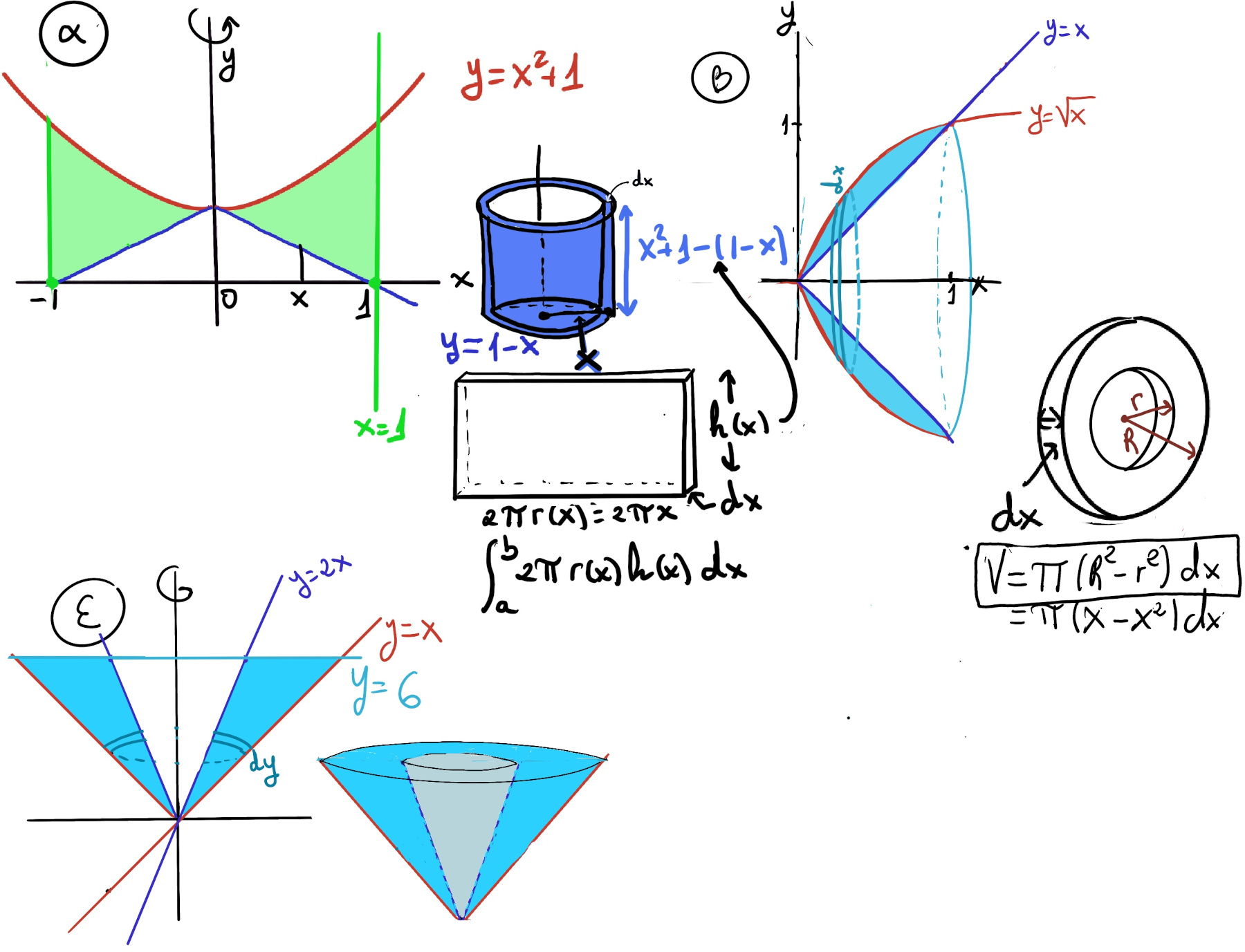
It is revolved about the y-axis, we can use the method of cylindrical shells. The volume of the solid formed by revolving a region R, bounded by x = a and x = b, around a vertical axis is $V = 2π\int_{a}^{b} r(x)h(x)dx$ where r(x) is the distance from the axis of rotation to x (the radius of the shell) and h(x) is the height of the solid at x (the height of the shell).

1. Let’s find the points of intersections, $x^2+1 = -x + 1 ↭ x^2 + x = 0 ↭ x(x + 1) = 0$ ⇒ x = 0 or x = -1. We only consider x = 0 since the region is bounded by x = 1.
2. Let’s set up the integral for the volume using cylindrical shells, the radius of each shell is r = x, the thickness dx, and the heigh of each shell is h = (x²+1)-(-x+1).
3. Therefore, the volume is $2π\int_{0}^{1} x(x^2+1-(-x+1))dx = 2π\int_{0}^{1} x(x^2+1+x-1)dx = 2π\int_{0}^{1} (x^3+x^2)dx = 2π(\frac{x^4}{4}+\frac{x^3}{3})\bigg|_{0}^{1} = 2π(\frac{1}{4}+\frac{1}{3}) = 2π\frac{7}{12} = \frac{7π}{6}.$

• Find the volume of revolution if the region enclosed in the first quadrant by y = x and y = $\sqrt{x}$ is rotated about the x-axis.

We must find the volume of revolution of y = $\sqrt{x}$ (V₁) and subtract the volume of revolution of y = x (V₂) (Figure β).

x-intercepts, $x = \sqrt{x} ↭(1st~quadrant)~ x^2 = x ↭ x(x-1) = 0$ ⇒ x = 0 and 1.

V₁ = $\int_{0}^{1} π(\sqrt{x})^2dx - \int_{0}^{1} π(x^2) = \int_{0}^{1} πxdx - \int_{0}^{1} πx^2 = \int_{0}^{1} π(x-x^2)dx = π(\frac{x^2}{2}-\frac{x^3}{3})\bigg|_{0}^{1} = π(\frac{1}{2}-\frac{1}{3}) = π\frac{3-2}{6}= \frac{1π}{6}≈0.5236units^3$

• Find the volume of the solid generated when the region bounded by y = x, y = 2x, and y = 6 is revolved about the y-axis (Figure ε)

V = $\int_{0}^{6} π(y^2-(\frac{y}{2})^2)dy = π\int_{0}^{6} (y^2-\frac{y^2}{4})dy = π\int_{0}^{6}\frac{3}{4}y^2dy = \frac{3}{4}π\frac{y^3}{3}\bigg|_{0}^{6} = \frac{3}{4}π\frac{6^3}{3} = \frac{216}{4}π = 54π ≈ 169.646units^3$

• $\int_{-∞}^{∞} e^{-t^{2}}dt = \int_{-∞}^{0} e^{-t^{2}}dt + \int_{0}^{∞} e^{-t^{2}}dt = $[Symmetry]$2\int_{0}^{∞} e^{-t^{2}}dt$ =[Recall The Second Fundamental Theorem of Calculus. If f is a continuous function and c is a constant, then f has a unique antiderivative A that satisfies A(c) = 0, and that antiderivative is given by the rule A(x) = $\int_{c}^{x} f(t)dt$. F(x) = $\int_{0}^{x} e^{-t^{2}}dt$] 2F(∞) =[F(∞)=$\frac{\sqrt{π}}{2}$ and this is a difficult integral] $\sqrt{π}$ -Figure 1.b.-.

• Volume of the region bounded by y = x-x³ and the x-axis in the first quadrant rotated around the y-axis.

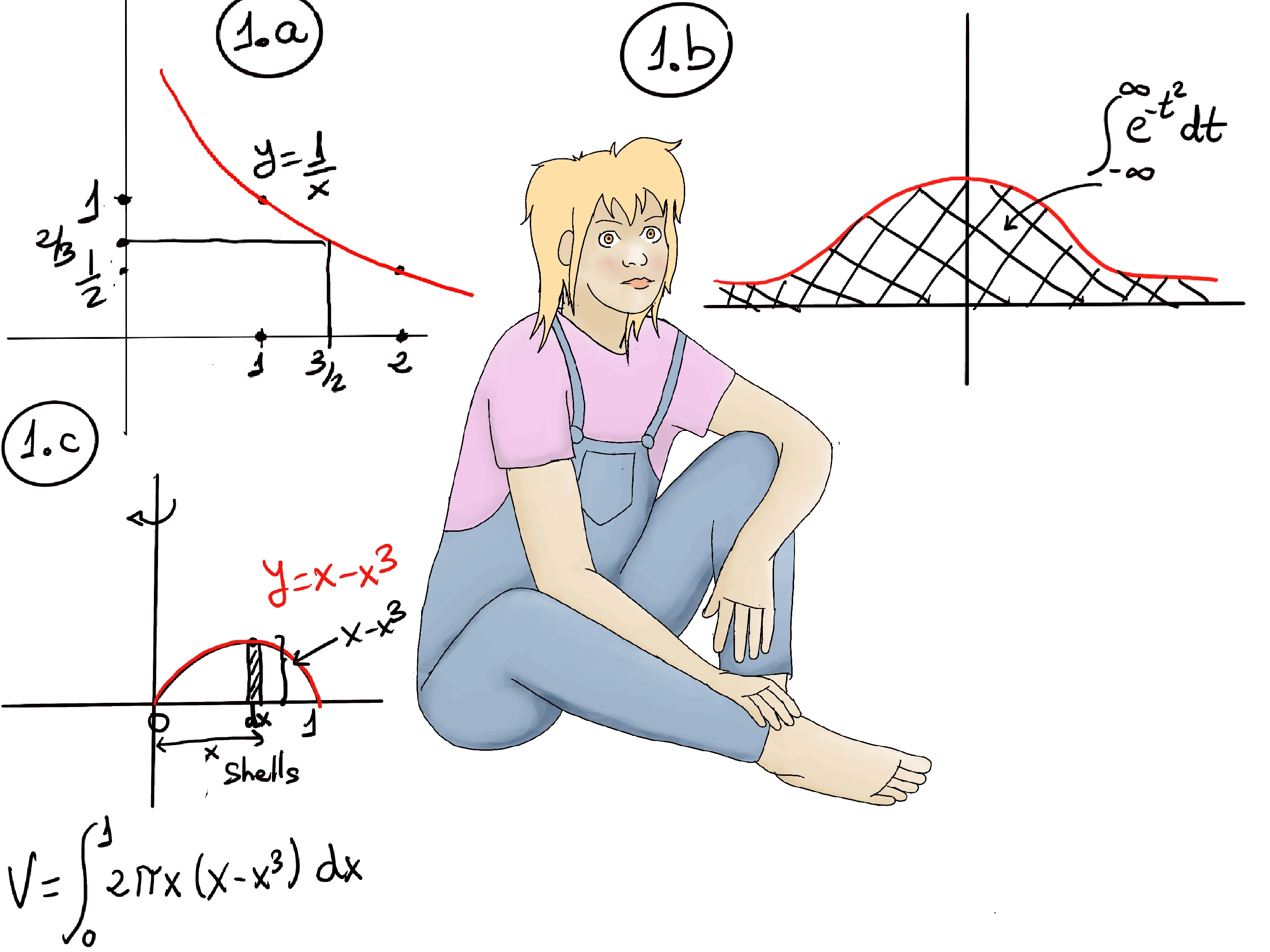
Solution: Figure 1.c.

Intersections of y = x -x³ and y = 0 ↭ x - x³ = 0 ↭ x(1 -x²) = 0 ↭ x = 0, 1 (we are working in the first quadrant).

V = $\int_{0}^{1} 2π(x-x^3)dx = π(x^2-\frac{x^4}{2})\bigg|_{0}^{1} = π(1-\frac{1}{2}) = \frac{π}{2}$.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.