Determining volumes

Once again, you show all the sensitivity of a blunt axe, J. K. Rowling.

Recall

Antiderivatives are fundamental concepts in calculus. They are the inverse operation of derivatives.

Given a function f(x), an antiderivative, also known as indefinite integral, F, is the function that can be differentiated to obtain the original function, that is, F’ = f, e.g., 3x² -1 is the antiderivative of x³ -x +7 because $\frac{d}{dx} (x^3-x+7) = 3x^2 -1$. Symbolically, we write F(x) = $\int f(x)dx$.

The process of finding antiderivatives is called integration.

The Fundamental Theorem of Calculus states roughly that the integral of a function f over an interval is equal to the change of any antiderivate F (F'(x) = f(x)) between the ends of the interval, i.e., $\int_{a}^{b} f(x)dx = F(b)-F(a)=F(x) \bigg|_{a}^{b}$

Determining volumes

Calculating volumes with integrals is tricky and involves a variety of techniques such as the following ones:

• Determining Volumes by Slicing. Let’s suppose a solid, e.g., a loaf of bread sitting on the counter, in order to calculate its volume, we want to slice the solid into pieces, calculate the volume of each slice and sum up the volumes of all slices using an integral. When we use this method with solids of revolution, it is often called the Disk Method because the slices used to approximate the volume are disks.

Solids of revolution are three-dimensional shapes formed by rotating a two-dimensional curve or region about an axis in space. When a curve or region in the plane is rotated around an axis, it creates a solid shape. The resulting solid is composed of a series of disks. The volume of each disk is calculated, and then these volumes are integrated over the given interval.

Let’s use the slicing method to find the volume of the solid of revolution bounded by the graphs of y = f(x), x = a, and x = b, and rotated about the x-axis. Since the solid was formed by revolving the region around the x-axis, the cross-sections are disks. The area of the cross section is the area of a circle, and its radius is f(x), hence A(x) = πr² = π·f(x)² (Figure 1.a and Figure 1.b) and V = $\int_{a}^{b} A(x)dx = \int_{a}^{b} π(f(x))^2dx$ (this is the case if and only if the axis of rotation is the x-axis).

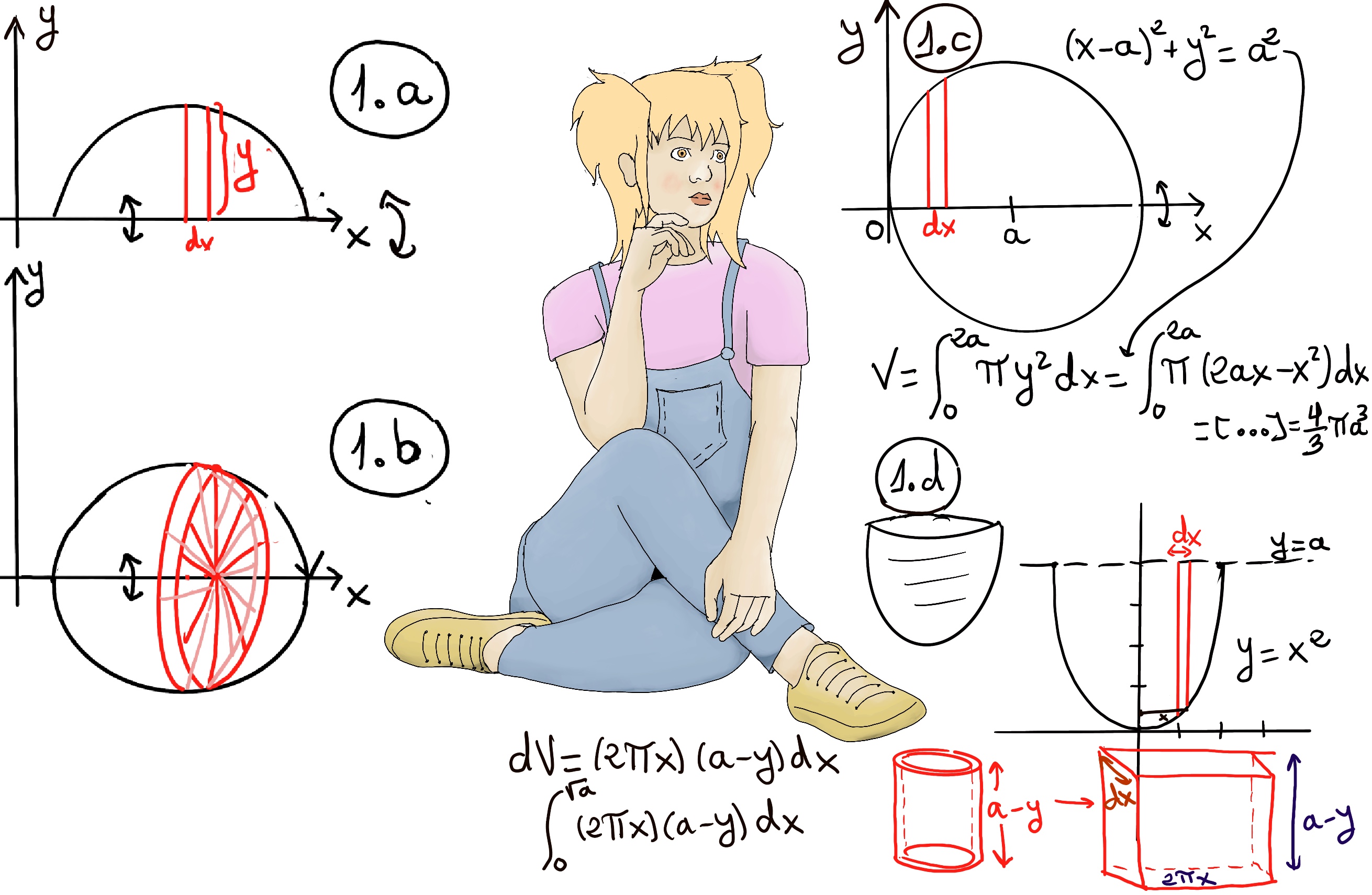
Example. Find the volume of a sphere of radius a.

Taking into consideration that the formula of a circle is as follows (x -a)² + y² = a² ⇒ y² = a² -(x -a)² = a² -(x² -2ax +a²) = 2ax -x² (Figure 1.c.).

V = $\int_{0}^{2a} π(2ax-x^2)dx = π(ax^2-\frac{x^3}{3})\bigg|_{0}^{2a} = π(4a^3-\frac{8a^3}{3}) = (\frac{12}{3}-\frac{8}{3})πa^3 = \frac{4}{3}πa^3$.

Futhermore, V(x) is the volume of a ball’s portion of width x, e.g., V(a) =[the volume of half of the ball] $π(ax^2-\frac{x^3}{3})\bigg|_{0}^{a} = π(a^3-\frac{a^3}{3}) = \frac{2}{3}πa^3$, that is obviously half the volume of the whole ball.

• The shell method. It is used when the axis of rotation is parallel to the axis of integration. Instead of slicing the solid perpendicular to the axis of rotation creating cross-sections, we now slice it parallel to the axis of rotation, creating “shells.”

We can visualize the solid as composed of cylindrical shells. Let a solid be formed by revolving a region R, bounded by x = a and x = b, around the vertical axis. The volume of one shell with thickness Δx is (2πr·h)Δx, and the volume of the solid is $2π\int_{a}^{b} r(x)h(x)dx$ where r(x) is the distance from the axis of rotation to x (the radius of a shell), and h(x) is the height of the solid at x, i.e., the height of the shell.

Example. Calculate the volume of the solid formed by rotating the triangular region determined by the points (0, 1), (1, 1), and (1, 3) about the line x = 3 (Figure B).

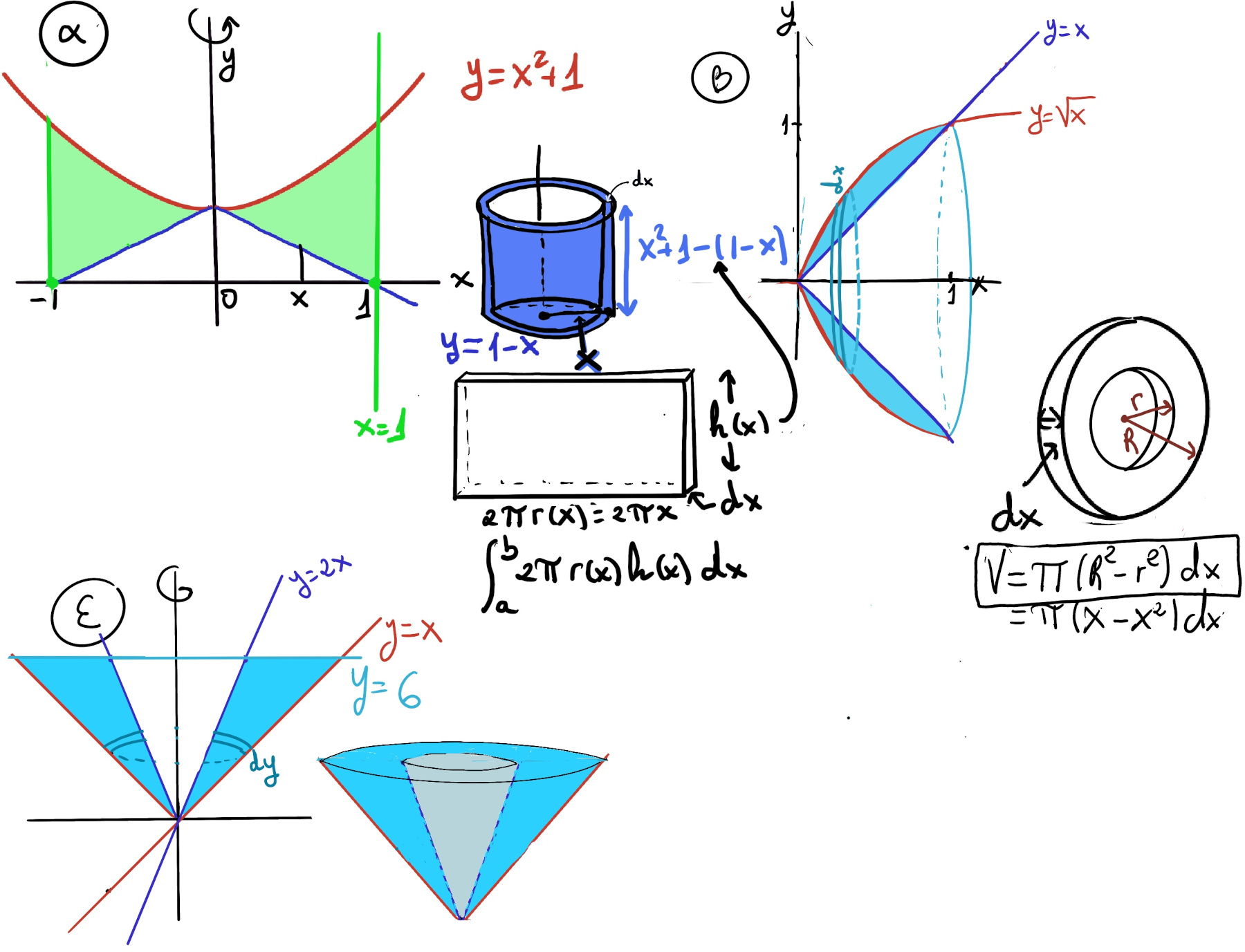
The volume of the solid is $2π\int_{0}^{1} r(x)h(x)dx$ where a = 0, b = 1, r(x) = 3 - x is the distance from the axis of rotation to x (the radius of a shell), and h(x) = 2x + 1 - 1 = 2x (y = 2x +1 is the line that connects (0, 1) and (1, 3)) is the height of the solid at x

V = $2π\int_{0}^{1} r(x)h(x)dx = 2π\int_{0}^{1} (3-x)2xdx = 2π\int_{0}^{1} (6x -2x^2)dx = 2π(\frac{6x^2}{2}-\frac{2x^3}{3}) = 2π(3x^2-\frac{2x^3}{3})\bigg|_{0}^{1} = 2π(3-\frac{2}{3}) = 2π\frac{7}{3} = \frac{14π}{3}≈14.66 units^3.$

• Washer method. Some solids of revolution have cavities in the middle; they are not solid all the way to the axis of revolution. In other cases, cavities arise when the region is bounded by two functions, say f(x) and g(x).

In this particular case, the slices used to approximate the volume are not disks, but washers (disks with holes in the center, so we subtract the area of the inner circle from the area of the outer circle), so the solid can be visualized as composed of nested washers. Its volume is $V = π\int_{a}^{b} (R(x)^2 -r(x)^2)dx$, where R(x) is the outer radius and r(x) is the inner radius.

Suppose f and g are continuous, non-negative functions, f(x) ≥ g(x) over [a, b], then the volume of the solid of revolution formed by revolving the region above by f, below by g, on the left by x = a, and on the right by x = b about the x-axis is $V = π\int_{a}^{b} (R(x)^2 -r(x)^2)dx = π\int_{a}^{b} (f(x)^2 -g(x)^2)dx$.

Exercise. Find the volume of revolution if the region enclosed in the first quadrant by y = $\sqrt{x}$ and y = x² is rotated about the x-axis (Figure C).

x-intercepts, $\sqrt{x} = x^2 ↭ x = x^4 ↭ x^4-x = 0 ↭ x(x^3-1) = 0$ ⇒[First quadrant] x = 0 and 1.

$V = π\int_{a}^{b} (R(x)^2 -r(x)^2)dx = π\int_{a}^{b} (f(x)^2 -g(x)^2)dx = π\int_{0}^{1} ((\sqrt{x})^2 -(x^2)^2)dx = π\int_{0}^{1} (x - x^4)dx = π(\frac{x^2}{2}-\frac{x^5}{5})\bigg|_{0}^{1} = π(\frac{1}{2}-\frac{1}{5}) = π\frac{5-2}{10}= \frac{3π}{10}units^3$

Solved exercises

• Calculate the volume of the sphere by integrating vertically (Figure iii).

We are going to name x the vertical direction, a is the radius, and A(x) the cross-sectional area function.

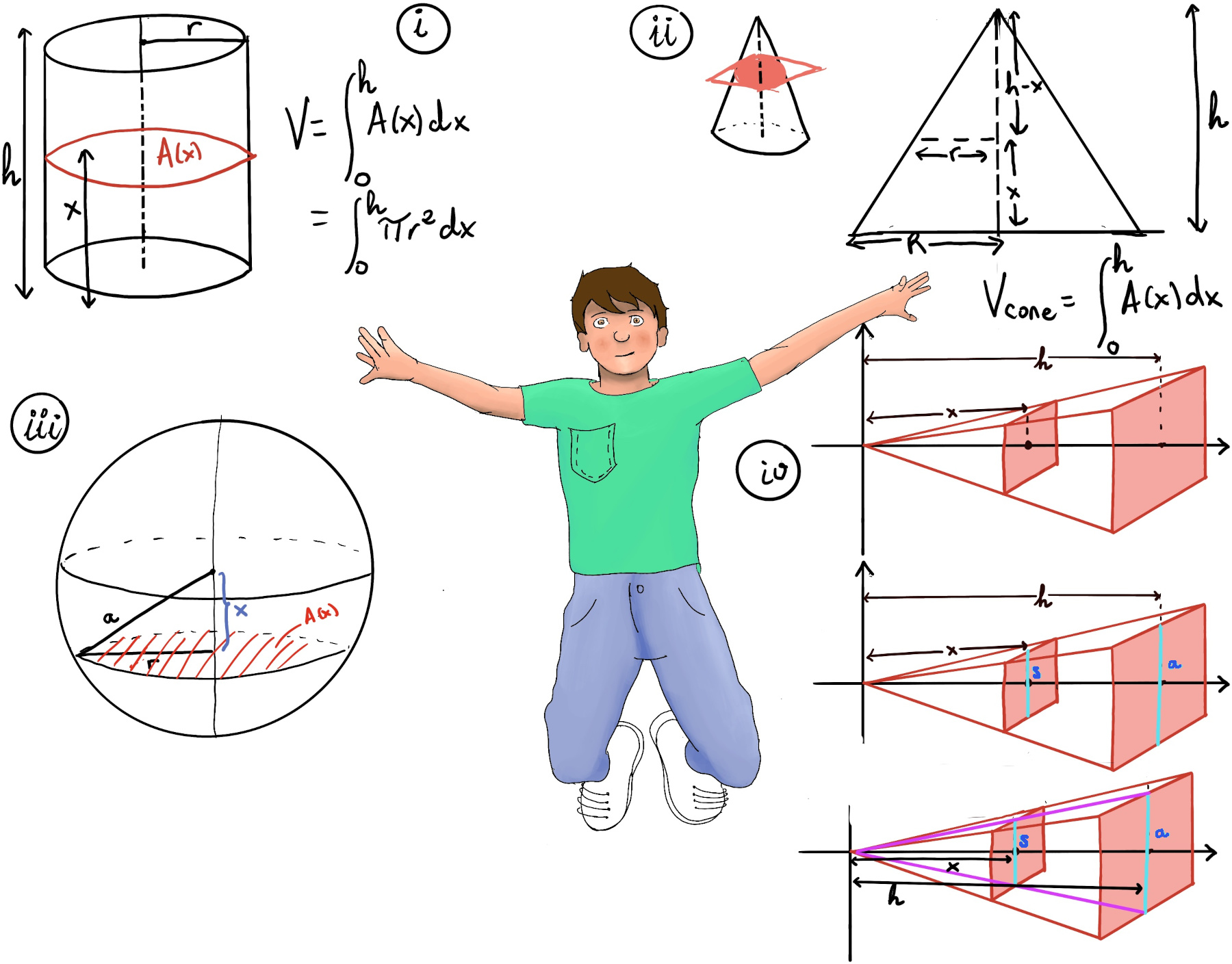
Then, by the Pythagorean theorem $r = \sqrt{a^2-x^2}, A(x) = πr^2 = π(a^2-x^2), V = \int_{-a}^{a} π(a^2-x^2)dx = \int_{-a}^{a} πa^2dx -π\int_{-a}^{a} x^2dx = πa^2x-π\frac{x^3}{3}\bigg|_{-a}^{a} = πa^3-π\frac{a^3}{3}-(-πa^3-π\frac{-a^3}{3}) = 2πa^3-2π\frac{a^3}{3} = 4π\frac{a^3}{3}$

• Calculate the volume of a right cylinder.

A right circular cylinder is a three-dimensional geometric shape having two parallel bases on both ends and whose elements are perpendicular to its base (Figure i).

We are going to integrate along the height of the cylinder and choose x to be the vertical direction. A(x) = πr² describes the cross-sectional area (it is just a circle) of our cylinder at a height of x.

Volumen_cylinder = $\int_{0}^{h} A(x)dx = \int_{0}^{h} πr^2dx = πr^2x\bigg|_{0}^{h} = πr^2h.$

• Calculate the volume of a pyramid.

A pyramid is a polyhedron for which the base is a polygon and all lateral faces are triangles (Figure iv). Since the base is a square, the cross-sections are squares, too. V = $\int_{0}^{h} A(x)dx =\int_{0}^{h} s^2dx$ where we are working with a pyramid with a base “a” and height “h” and s(x) is the length of the cross-section’s side.

We can observe two similar or congruent triangles ⇒ $\frac{s}{x} = \frac{a}{h} ⇒ s = \frac{ax}{h} ⇒ V = \int_{0}^{h} s^2dx = \int_{0}^{h} \frac{a^2x^2}{h^2}dx = \frac{a^2}{h^2}\int_{0}^{h}x^2dx = \frac{a^2}{h^2}·\frac{x^3}{3}\bigg|_{0}^{h} = \frac{a^2}{h^2}·\frac{h^3}{3}= \frac{a^2h}{3}$.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.