Determining volumes II

Of course I’m in shape. Round is a shape.

Recall

Antiderivatives are fundamental concepts in calculus. They are the inverse operation of derivatives.

Given a function f(x), an antiderivative, also known as indefinite integral, F, is the function that can be differentiated to obtain the original function, that is, F’ = f, e.g., 3x² -1 is the antiderivative of x³ -x +7 because $\frac{d}{dx} (x^3-x+7) = 3x^2 -1$. Symbolically, we write F(x) = $\int f(x)dx$.

The process of finding antiderivatives is called integration.

The Fundamental Theorem of Calculus states roughly that the integral of a function f over an interval is equal to the change of any antiderivate F (F'(x) = f(x)) between the ends of the interval, i.e., $\int_{a}^{b} f(x)dx = F(b)-F(a)=F(x) \bigg|_{a}^{b}$

Calculating volumes with integrals is tricky and involves a variety of techniques such as slicing, the shell method, and the washer method.

Solved examples

• A teacher has a paperweight made so that its base is the shape of the region between the x‐axis and one arch of the curve y = 2·sin(x) (units measured in centimeters). Each cross section cut perpendicular to the x‐axis is a semicircle whose diameter runs from the x‐axis to the curve. Calculate the volume of the paperweight (Figure 1).

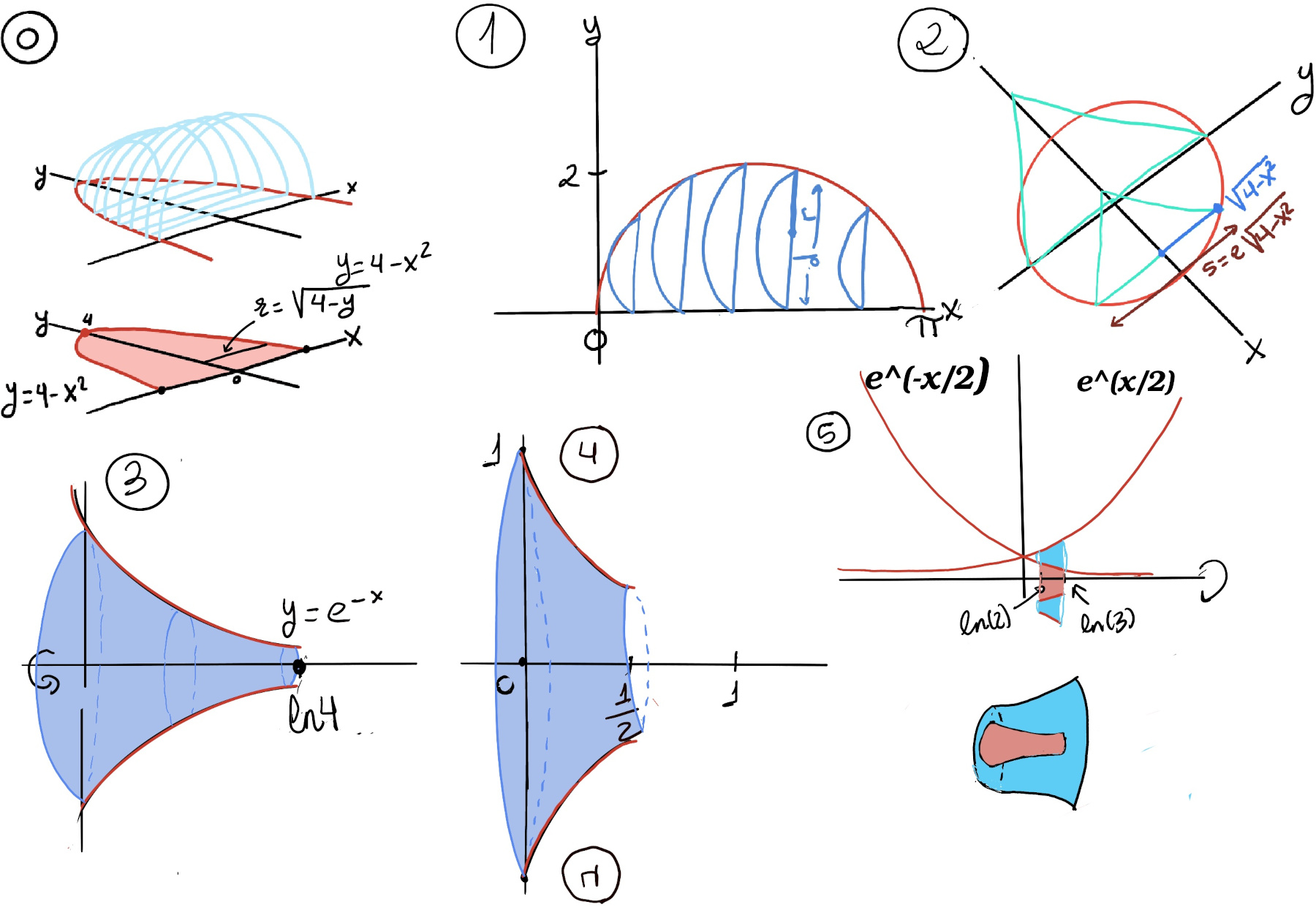
This is quite simple, A =[Each cross section is a semicircle] $\frac{1}{2}πr^2 =$ [d = 2sin(x) ⇒ r = sin(x)] $\frac{1}{2}π(sin^2x)$.

V = $\int_{0}^{π} \frac{1}{2}π(sin^2x)dx = \frac{1}{2}π\int_{0}^{π}(sin^2x) =\frac{1}{2}π\int_{0}^{π}\frac{1}{2}(1-cos(2x))dx = \frac{1}{4}π·(\int_{0}^{π} dx - \int_{0}^{π} cos(2x)dx) = \frac{1}{4}π·(x -\frac{1}{2}sin(2x))\bigg|_{0}^{π} = \frac{1}{4}π(π-\frac{1}{2})sin(2π)-(0-\frac{1}{2}sin(0)) = \frac{1}{4}π^2 ≈ 2.467 cm^3$

• Find the volume of a solid whose base is the region inside the circle x² + y² = 4, and the cross sections taken are perpendicular to the x‐axis and equilateral triangles (Figure 2)

The area of an equilateral triangle can be calculated using the formula: A(x) = $\frac{\sqrt{3}}{4}s^2$ where A is the area and s is the length of one side of the equilateral triangle. Since $x^2+y^2=4 ⇒ y^2=4-x^2$ ⇒[First quadrant] $y = \sqrt{4-x^2} ⇒ S = 2\sqrt{4-x^2} ⇒ A(x) = \frac{\sqrt{3}}{4}4(4-x^2) = \sqrt{3}(4-x^2)$

V =[the circle x² + y² = 4 has a radius r = 2 and x ∈ [-2, 2]] $\int_{-2}^{2} \sqrt{3}(4-x^2)dx = \sqrt{3}(4x -\frac{1}{3}x^3)\bigg|_{-2}^{2} = \sqrt{3}(8 -\frac{1}{3}8-(-8-\frac{1}{3}(-8))) = \sqrt{3}(8 -\frac{1}{3}8+8+\frac{1}{3}(-8)) = \sqrt{3}(16-\frac{16}{3}) = \sqrt{3}(\frac{48}{3}-\frac{16}{3}) = \frac{32·\sqrt{3}}{3}$

• Calculate the volume of the solid whose base is the triangle with vertices (0, 0), (2, 0), and (2, 0) and whose cross sections are perpendicular to the base and parallel to the​ y-axis are semicircles (Figure E).

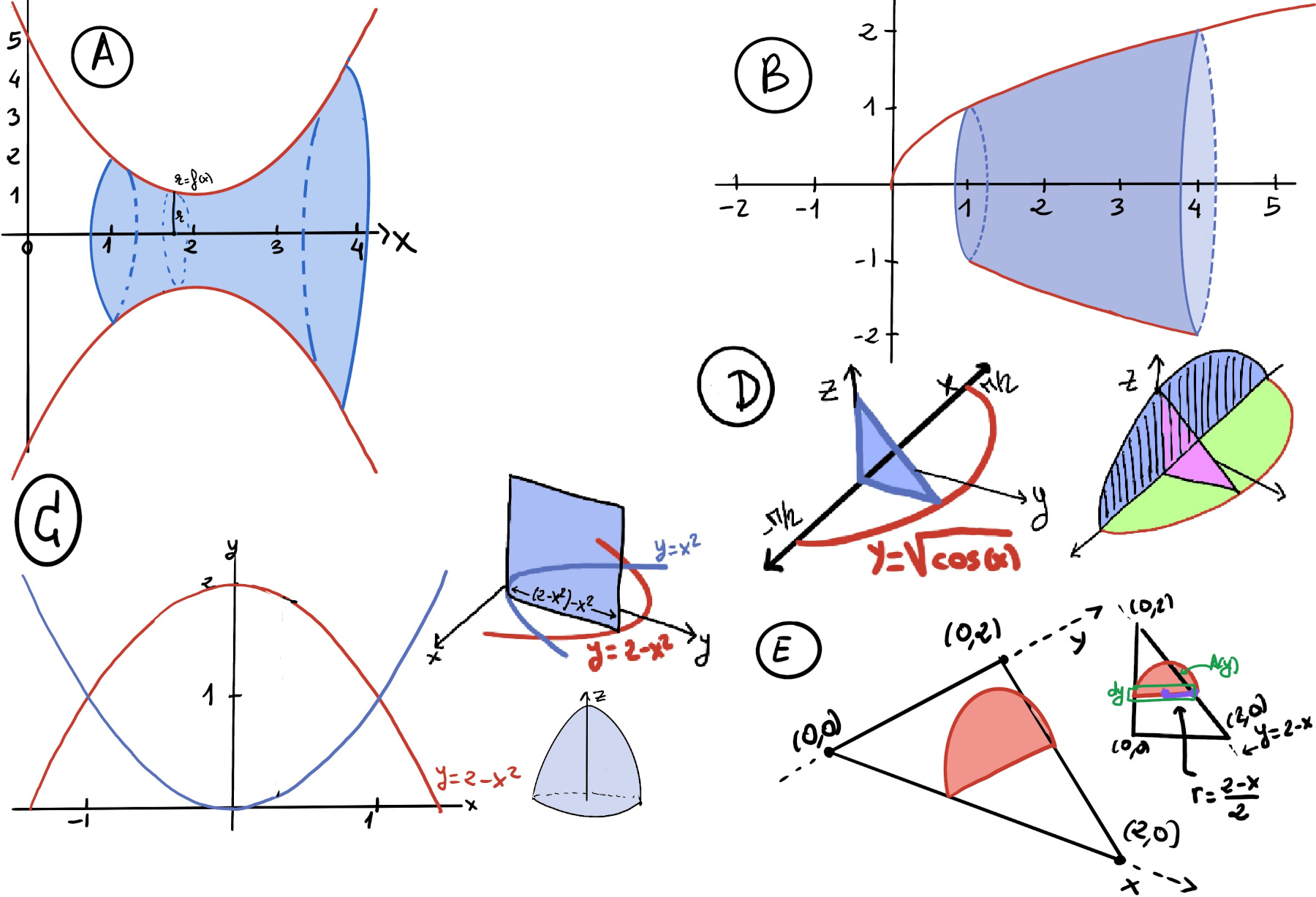
The volume of a solid that extends from y = a to y = b and has a known integrable cross-sectional area A(y) perpendicular to the x-axis is given by the formula for the general slicing method, that is, V = $\int_{a}^{b} A(y)dx = \int_{0}^{2} A(y)dy$.

The equation of the line passing through two points (x₁, y₁) and (x₂, y₂) is $y -y_1 = \frac{y_2-y_1}{x_2-x_1}(x-x_1)$ ⇒ The line that crosses between (0, 2) and (2, 0) is $y-2=\frac{-2}{2}(x-0) ↭ y - 2 = -x$ ↭ y = 2 - x.

A(y) =[Formula for the area of a semicircle] $\frac{π}{2}r^2$ where r is the radius =[Since the diameter is 2-x, the radius of the semicircle is half that quantity, but we need it as a function of y. y = 2-x ↭ x = 2-y] $\frac{π}{2}*(\frac{2-y}{2})^2$

V = $\int_{0}^{2} A(y)dy = \int_{0}^{2} \frac{π}{2}*(\frac{2-y}{2})^2dy = \frac{π}{8} \int_{0}^{2} (4-4y+y^2)dy = \frac{π}{8}(4y+\frac{-4}{2}y^2+\frac{y^3}{3}) = \frac{π}{8}(4y-2y^2+\frac{y^3}{3}) = \bigg|_{0}^{2} = \frac{π}{8}(8-8+\frac{8}{3}) = \frac{π}{3}.$

• Compute the volume of the solid whose base is the region between the inverted parabola y = 4-x² and the x-axis, and whose vertical cross sections perpendicular to the y-axis are semicircles (Figure 0).

1. x-intersects: 4 -x² = 0, x^2 = 4, x = ±2.
2. V = $\int_{a}^{b} A(y)dy = \int_{0}^{4} A(y)dy.$
3. Area = $\frac{1}{2}πr^2$ where r = 4 - x² ⇒[However, we want r = r(y), y = 4 -x² ↭ x² = 4 -y] r = $\sqrt{4 -y}, Area = \frac{1}{2}π\sqrt{4 -y}^2 = \frac{1}{2}π(4-y)$
4. V = $\int_{0}^{4} A(y)dy = \int_{0}^{4} \frac{1}{2}π(4-y)dy = \frac{1}{2}π(4y -\frac{1}{2}y^2)\bigg|_{0}^{4} = \frac{1}{2}π(16-8)=4π$

• Calculate the volume of a right circular cone.

A cone is a three-dimensional solid geometric shape having a circular base and a pointed edge at the top called the apex. A right circular cone is a cone where the axis of the cone is the line meeting the vertex to the midpoint of the circular base (Figure ii).

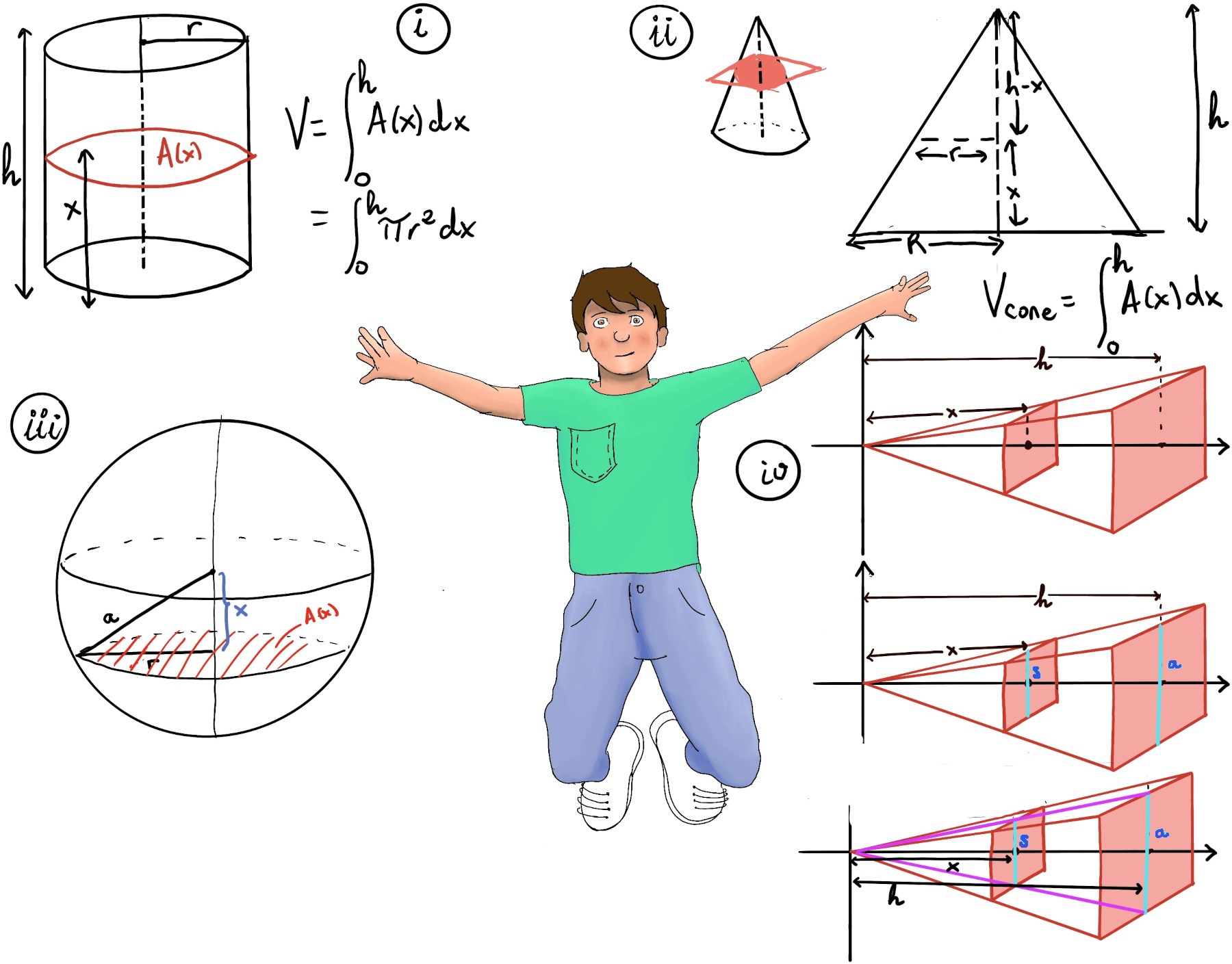
We are going to integrate along the height of the cone and choose x to be the vertical direction. The cross sections are simply circles, but the radius varies from the base of the cone to the apex.

By similarity of triangles, $\frac{r}{h-x} = \frac{R}{h} ⇒ r = \frac{R}{h}(h-x) ⇒ A(x) = π\frac{R^2}{h^2}(h-x)^2, V = \int_{0}^{h} π\frac{R^2}{h^2}(h-x)^2dx = π\frac{R^2}{h^2}\int_{0}^{h}(h-x)^2dx = $[By substitution of variables u = h -x, du = -dx, u₁ =h, u₂ = 0] $π\frac{R^2}{h^2}(-\int_{h}^{0}u^2du) = π\frac{R^2}{h^2}\frac{-u^3}{3}\bigg|_{h}^{0} = π\frac{R^2}{h^2}(-0+\frac{h^3}{3}) = \frac{π}{3}R^2h$

• Find the volume of the solid generated when the region R bounded by y = e^-x, y = 0, x = 0, and x = ln(4) is revolved about the x-axis (Figure 3).

The solid of revolution is formed by revolving the region R around the x-axis ⇒ the cross-sections are circles, A(x) = πr² where r = f(x)

V = $\int_{0}^{ln(4)} π(e^{-x})^2dx = \int_{0}^{ln(4)} π(e^{-2x})dx = π\frac{-1}{2}e^{-2x}\bigg|_{0}^{ln(4)} = \frac{-π}{2}(e^{-2ln(4)}-e^0) = \frac{-π}{2}(e^{ln(4)^{-2}}-1) = \frac{-π}{2}(\frac{1}{16}-1) = \frac{-π}{2}·\frac{-15}{16} = \frac{15π}{32}$

• Find the volume of the solid generated when the region bounded by y = $\frac{1}{\sqrt[4]{1-x^2}}$, y = 0, x = 0, and x = 1/2 is revolved about the x-axis (Figure 4).

The solid of revolution is formed by revolving the region around the x-axis ⇒ the cross-sections are circles, A(x) = πr² where r = f(x)

V = $\int_{0}^{\frac{1}{2}} π(\frac{1}{\sqrt[4]{1-x^2}})^2dx = π\int_{0}^{\frac{1}{2}} \frac{1}{\sqrt{1-x^2}}dx = π·sin^{-1}(x)\bigg|_{0}^{\frac{1}{2}} = π·(sin^{-1}(\frac{1}{2})-sin^{-1}(0)) = π(\frac{π}{6}-0) = \frac{π^2}{6}.$

• Find the volume of the solid of revolution bounded by the graphs of f(x) = x^2 -4x +5, x = 1 and x = 4, and rotated about the x-axis (Figure A).

The solid of revolution is formed by revolving the region around the x-axis ⇒ the cross-sections are circles, A(x) = πr² where r = f(x) = x²-4x +5, and the volume is $\int_{1}^{4} πr^2dx = \int_{1}^{4} π(x^2-4x+5)^2dx = π\int_{1}^{4}(x^4-8x^3+26x^2-40x+25) = π(\frac{x^5}{5}-8\frac{x^4}{4}+26\frac{x^3}{3}-40\frac{x^2}{2}+25x) = π(\frac{x^5}{5}-2x^4+26\frac{x^3}{3}-20x^2+25x)\bigg|_{1}^{4} ≈ 49.009$

Let f be continuous and non-negative, let R be the region bounded above by the graph of x, below by the x-axis, on the left by x = a, and on the right by x = b. Then, the volume of the solid of revolution formed by revolving R around the x-axis is given by V = $\int_{a}^{b} πf(x)^2dx$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.