Derivate 4. Inverse functions.

The man who asks a question is a fool for a minute, the man who does not ask is a fool for life, Confucius.

Recall

The derivative of a function at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. It is the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable.

Definition. A function f(x) is differentiable at a point “a” of its domain, if its domain contains an open interval containing “a”, and the limit $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$ exists, f’(a) = L = $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$. More formally, for every positive real number ε, there exists a positive real number δ, such that for every h satisfying 0 < |h| < δ, then |L-$\frac {f(a+h)-f(a)}{h}$|< ε.

1. Power Rule: $\frac{d}{dx}(x^n) = nx^{n-1}$.
2. Sum Rule: $\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))$
3. Product Rule: $\frac{d}{dx}(f(x) \cdot g(x)) = f’(x)g(x) + f(x)g’(x)$.
4. Quotient Rule: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f’(x)g(x) - f(x)g’(x)}{(g(x))^2}$
5. Chain Rule: $\frac{d}{dx}(f(g(x))) = f’(g(x)) \cdot g’(x)$
6. $\frac{d}{dx}(e^x) = e^x, \frac{d}{dx}(\ln(x)) = \frac{1}{x}, \frac{d}{dx}(\sin(x)) = \cos(x), \frac{d}{dx}(\cos(x)) = -\sin(x), \frac{d}{dx}(\tan(x)) = \sec^2(x), \frac{d}{dx}(\arcsin(x)) = \frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arccos(x)) = -\frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arctan(x)) = \frac{1}{1 + x^2}.$

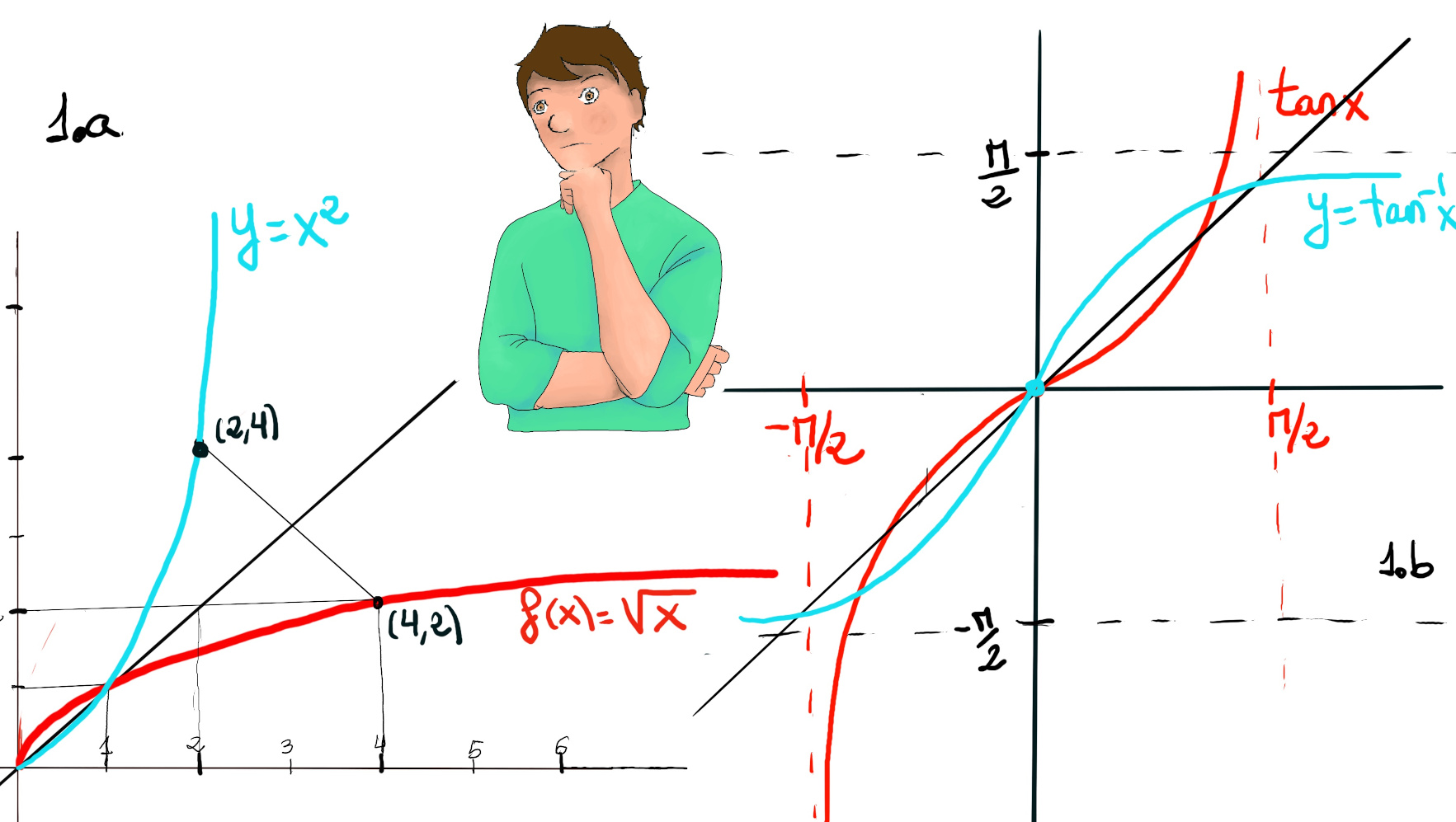
Loosely speaking, the inverse function of a function f is a function that undoes the operation of the original function. If f is a function that maps each element x in its domain to a unique element y in its codomain, then the inverse function, denoted as $f^{-1}$, maps each element y back to its corresponding x.

For a given function f, its inverse g(=f^-1) is a function that reverses its result (g reverses the input and output of the original function), g(f(x))=x. An example is f(x)=$\sqrt{x},$ (x ≥ 0) g(f(x))=x ↭ g(x)= x², -1.a.- The square function (x²) is the inverse of the square root function ($\sqrt{x}$). The natural logarithm function is the inverse of the exponential function (1.e.). Logarithmic functions are the inverses of exponential functions, y = a^x, f^-1(x) = log_a(x).

If you want to plot the graph of f^-1, you just need to reflect the graph of f(x) about the line y = x.

For an inverse function to exist, the original function must be both one-to-one (injective) and onto (surjective). A function is one-to-one if each element of the domain maps to a distinct (unique) element in the codomain, and it is onto if every element in the codomain is mapped to by at least one element in the domain or, in other words, has a pre-image in the domain.

To find the inverse of a function, you need to switch the roles of x and y, and then solve for y in terms of x. f(x) = $\frac{2x+5}{3x-2}$. $x = \frac{2y+5}{3y-1} ⇒ 3yx -x = 2y + 5 ⇒ y(3x-2) = x + 5 ⇒ f^{-1}(x) = \frac{x+5}{3x-2}.$ Another example is f(x) = x³ -1: x = y³ -1 ↭ y³ = x +1 ↭ $f^{-1}(x) = \sqrt[3]{x+1}$

Derivate of inverse functions

Inverse function theorem. Let f(x) be a a function that is both invertible and diferenciable and let $f^{-1}(x)$ be the inverse of f. Then, for all x satisfying $f'(f^{-1}(x))≠0, f^{(-1)'}(x) = \frac{1}{f'(f^{-1}(x))}$.

Proof.

By definition y = f^-1(x) ↭ x = f(y) ⇒[We differentiate both sides implicitly with respect to x using the Chain Rule] 1 = $f’(y)·\frac{dy}{dx} ⇒ \frac{dy}{dx} = \frac{1}{f’(y)}$⇒ [y = f^-1(x)] $f^{(-1)’}(x) = \frac{1}{f’(f^{-1}(x))}$∎

Solved examples

• Let f(x) = 3·x³+2x+2. Compute (f^-1)’(2).

f’(x) = 9x² + 2. The derivate of f^-1 is $\frac{d}{dx} f^{-1}(x) = \frac{1}{9y^2+2}$ where y = f^-1(x).

(f^-1)’(2) =[We need to calculate f^-1(2), f(x) = y = 3·x³+2x+2, we swap x↭y, 2 = x = 3·y³+2y+2, the solution is 0] $\frac{1}{9·0^2+2}= \frac{1}{2}$

• Let f(x) = x⁵+2x³+7x+1. Compute (f^-1)’(1).

f’(x) = 5x⁴ + 8x² + 7. The derivate of f^-1 is $\frac{d}{dx} f^{-1}(x) = \frac{1}{5y^4+8y^2+7}$ where y = f^-1(x).

(f^-1)’(1) =[It is easy to notice that f(0) = 1, hence f^-1(1) = 0] $\frac{1}{5·0^4+8·0^2+7} = \frac{1}{7}$.

• Find the equation of the tangent line to the inverse of y = f(x) = $x^5-2x^3+3x+2$ at P(4, 1)

It is important to realize that P(4, 1) lies on f^-1, since f(1) = 1 -2 +3 +2 = 4, f^-1(4) = 1.

f(x) = $x^5-2x^3+3x+2 ⇒ f’(x) = 5x^4-6x^2+3$. The derivate of f^-1 is $\frac{d}{dx} f^{-1}(x) = \frac{1}{5y^4-6y^2+3}$ where y = f^-1(x).

(f^-1)’(4) =[f^-1(4) = 1] $\frac{1}{5·1^4-6·1^2+3} = \frac{1}{2}$.

The equation of the tangent line to the graph of f^-1 at P(4, 1) is y -y₀ = m(x -x₀), that is y -1 = ¹⁄₂(x -4) ↭ y = ¹⁄₂(x -4) + 1.

• Use the inverse function theorem to find the derivate of g(x) = $\sqrt[3]{x}.$

The function g(x) = $\sqrt[3]{x}$ is the inverse of the function f(x) = x³, and we know that f’(x) = 3x².

By the inverse function theorem, $\frac{d}{dx} f^{-1}(x) = g’(x) = \frac{1}{3y^2}$ =[y = f^-1(x) = g(x)] $\frac{1}{3·(\sqrt[3]{x})^2} = \frac{1}{3·x^{\frac{2}{3}}} = \frac{1}{3}x^{\frac{-2}{3}}$

Derivatives of Inverse Trigonometric Functions

Inverse trigonometric functions are functions that perform the opposite operation of regular trigonometric functions, e.g., arcsine (sin^-1(x)), arccosine (cos^-1(x)), and arctangent functions (tan^-1(x)).

• y = tan^-1x ⇨ tany = x.

$\frac{d}{dx}(tany=x)⇨~ \frac{d}{dy}tany\frac{dy}{dx}=1⇨~ \frac{1}{cos^{2}y}\frac{dy}{dx}=1⇨~ y’=cos^{2}y$

$(tan^{-1}x)’=\frac{d}{dx}\tan^{-1}x=cos^{2}(y)$ [tan(y) = x ↭ $ \frac{sin(y)}{cos(y)} = x ⇒ sin(y) = x·cos(y) ⇒ (x·cos(y))^2+cos^2(y) = 1 ⇒ x^2·cos^2(y) +cos^2(y) = 1 ⇒ (x^2+1)·cos^2(y) = 1 ⇒ cosy = \frac{1}{\sqrt{1+x^{2}}}$] = $\frac{1}{1+x^{2}}$

• y = $tan^{-1}(\frac{1}{x+1})$. Let u = $\frac{1}{x+1} = (x+1)^{-1}⇒ u’ = (-1)·(x+1)^{-2}$

By the previous result and the chain rule, y’ = $\frac{1}{1+(\frac{1}{x+1})^{2}}·\frac{-1}{(x+1)^{2}} = \frac{1}{\frac{(x+1)^2+1}{(x+1)^2}}·\frac{-1}{(x+1)^{2}} = \frac{-1}{(x+1)^2+1} = \frac{-1}{x^2+2x+2}$

• y = sin^-1x ⇨ siny = x.

$\frac{d}{dx}siny=1⇨~ \frac{d}{dy}siny\frac{dy}{dx}=1⇨~ cosy\frac{dy}{dx}=1$

$y’= \frac{1}{cos(y)}=~ \frac{1}{\sqrt{1-sin^{2}y}}=~ \frac{1}{\sqrt{1-x^{2}}}$

$(sin^{-1}x)’=\frac{d}{dx}sin^{-1}x=~ \frac{1}{\sqrt{1-x^{2}}}$

• y = sin^-1(x³) ⇨ sin(y) = x³.

$\frac{d}{dx}sin(y) = 3x^2 ⇨~ \frac{d}{dy}sin(y)\frac{dy}{dx}=3x^2 ⇨~ cos(y)\frac{dy}{dx}=3x^2$

$(sin^{-1}(x^3))’=\frac{d}{dx}sin^{-1}(x^3)=~ \frac{3x^2}{cos(y)} = \frac{3x^2}{\sqrt{1-sin^{2}y}} = \frac{3x^2}{\sqrt{1-(x^3)^2}} = \frac{3x^2}{\sqrt{1-x^6}}$

• y = cos^-1(x) ⇒ cos(y) = x.

$\frac{d}{dx}cos(y) = 1 ⇨~ \frac{d}{dy}cos(y)\frac{dy}{dx}=1 ⇨~ -sin(y)\frac{dy}{dx}=1$

$(cos^{-1}(x))’=\frac{d}{dx}cos^{-1}(x)=~ \frac{-1}{sin(y)} = \frac{-1}{\sqrt{1-cos^{2}y}} = \frac{-1}{\sqrt{1-x^2}}.$

• y = cos^-1(5x -9) ⇒ cos(y) = 5x -9.

$\frac{d}{dx}cos(y) = 5 ⇨~ \frac{d}{dy}cos(y)\frac{dy}{dx}=5 ⇨~ -sin(y)\frac{dy}{dx}=5$

$(cos^{-1}(5x-9))’=\frac{d}{dx}cos^{-1}(5x-9)=~ \frac{-5}{sin(y)} = \frac{-5}{\sqrt{1-cos^{2}y}} = \frac{-5}{\sqrt{1-(5x-9)^2}}.$

• The secant is the reciprocal of the cosine, i.e., the ratio of the hypotenuse to the side adjacent to a given angle in a right triangle. y = secx = $\frac{1}{cosx} = (cosx)^{-1}$.

$\frac{d}{dx}secx =~(-1)(cosx)^{-2}(-sin(x))=\frac{sin(x)}{cos(x)^{2}}=\frac{1}{cos(x)}·\frac{sin(x)}{cos(x)} = sec(x)·tan(x).$

• $\frac{d}{dx}ln(secx)=\frac{(secx)’}{secx}=\frac{secx·tanx}{secx}=tanx$

• The cosecant is the reciprocal of the sine, i.e., the ratio of the hypotenuse to the side opposite a given angle in a right triangle. The arcsecant is the inverse of the secant function, y = csc^-1(x) = arcsin(¹⁄_x) ⇒[$(sin^{-1}x)’= \frac{1}{\sqrt{1-x^{2}}}$ and the Chain Rule] y’ = $\frac{1}{\sqrt{1-(\frac{1}{x})^{2}}}·\frac{-1}{x^2} = \frac{1}{\sqrt{\frac{x^2-1}{x^2}}}·\frac{-1}{x^2} = \frac{-1}{\frac{x^2\sqrt{x^2-1}}{|x|}} = \frac{-1}{\frac{|x||x|\sqrt{x^2-1}}{|x|}} = \frac{-1}{|x|\sqrt{x^2-1}}$

This expression holds true when x > 1 or x < -1 as the expression involves the square root of x² - 1, which must be non-negative.

$y’ = \begin{cases} \frac{1}{x\sqrt{x^2-1}}, &x > 1 \\ \frac{-1}{x\sqrt{x^2-1}}, &x < -1 \end{cases}$

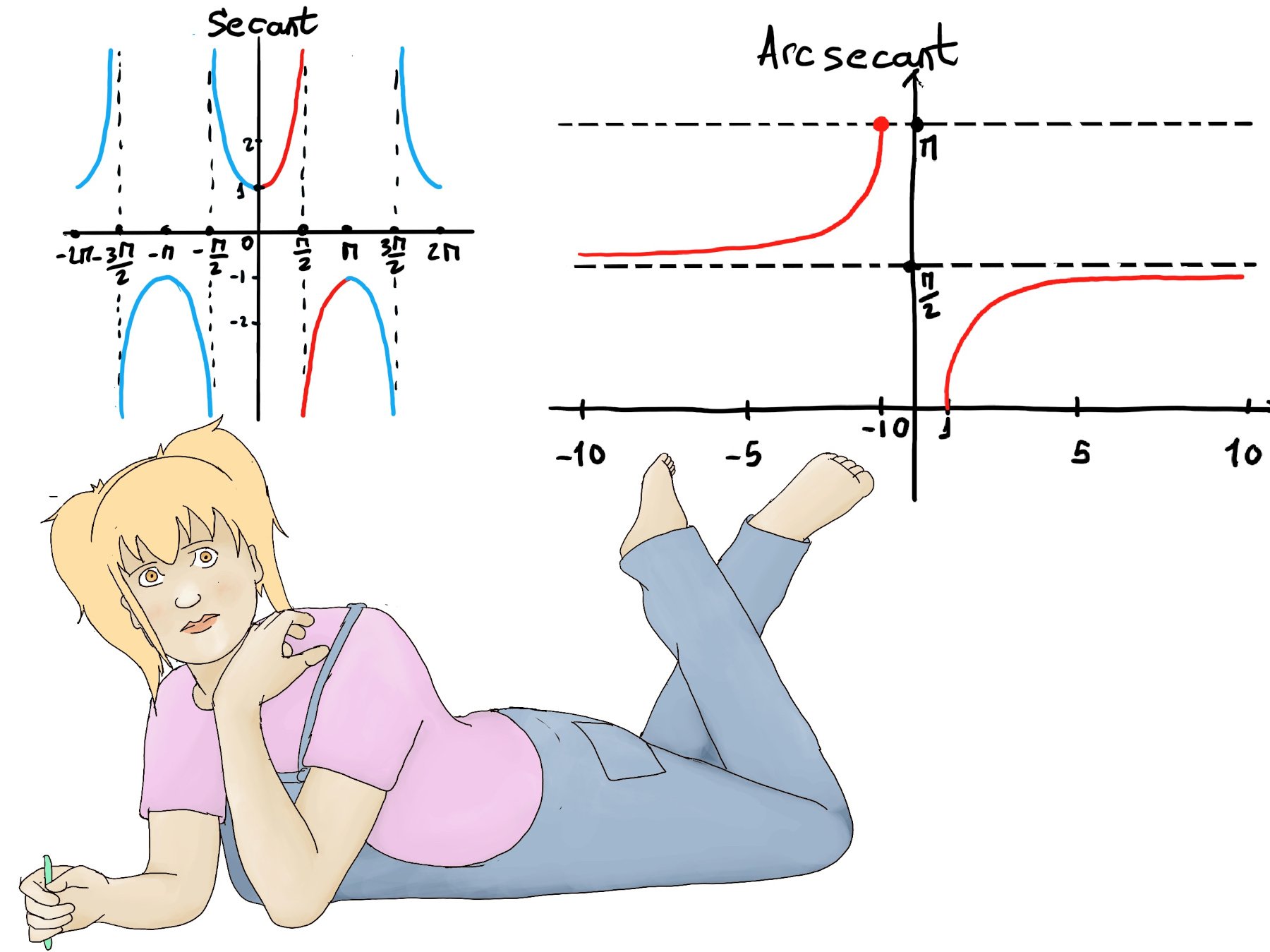
x > 1 ↭ 0 < arcsec(x) < ^π⁄₂, x < -1 ↭ ^π⁄₂ < arcsec(x) < π, Derivative of Arcsecant Function, ProofWiki

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus.
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
9. blackpenredpen.