Inverse functions

Get your facts first, then you can distort them as you please, Mark Twain.

“How are you doing pal?” “Sucking air, pumping blood, and slowly maintaining an undignified, insignificant existence while pretending but fooling nobody, to overcome a life of suppressed rage, unknown biases, dark areas, emotional rollercoaster, and most importantly, blatant denial,” Apocalypse, Anawim, #justtothepoint.

Recall

Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).

The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ.

Graphing functions involves the visual representation of a curve that reflects the behavior of a mathematical function on a coordinate plane, also known as the Cartesian plane. It is a two-dimensional space defined by two axes - the x-axis (horizontal) and the y-axis (vertical).

A systematic approach to graphing a function begins by constructing a table containing selected input values and their corresponding output values. By extending this table, we can plot the points on the coordinate plane and observe the pattern they form. Connecting these points reveals the shape of the curve, allowing us to gain insights into the behavior of the function across its domain. This process provides a visual means of understanding the relationships between different variables and aids in interpreting the overall characteristics of the function.

Inverse Functions

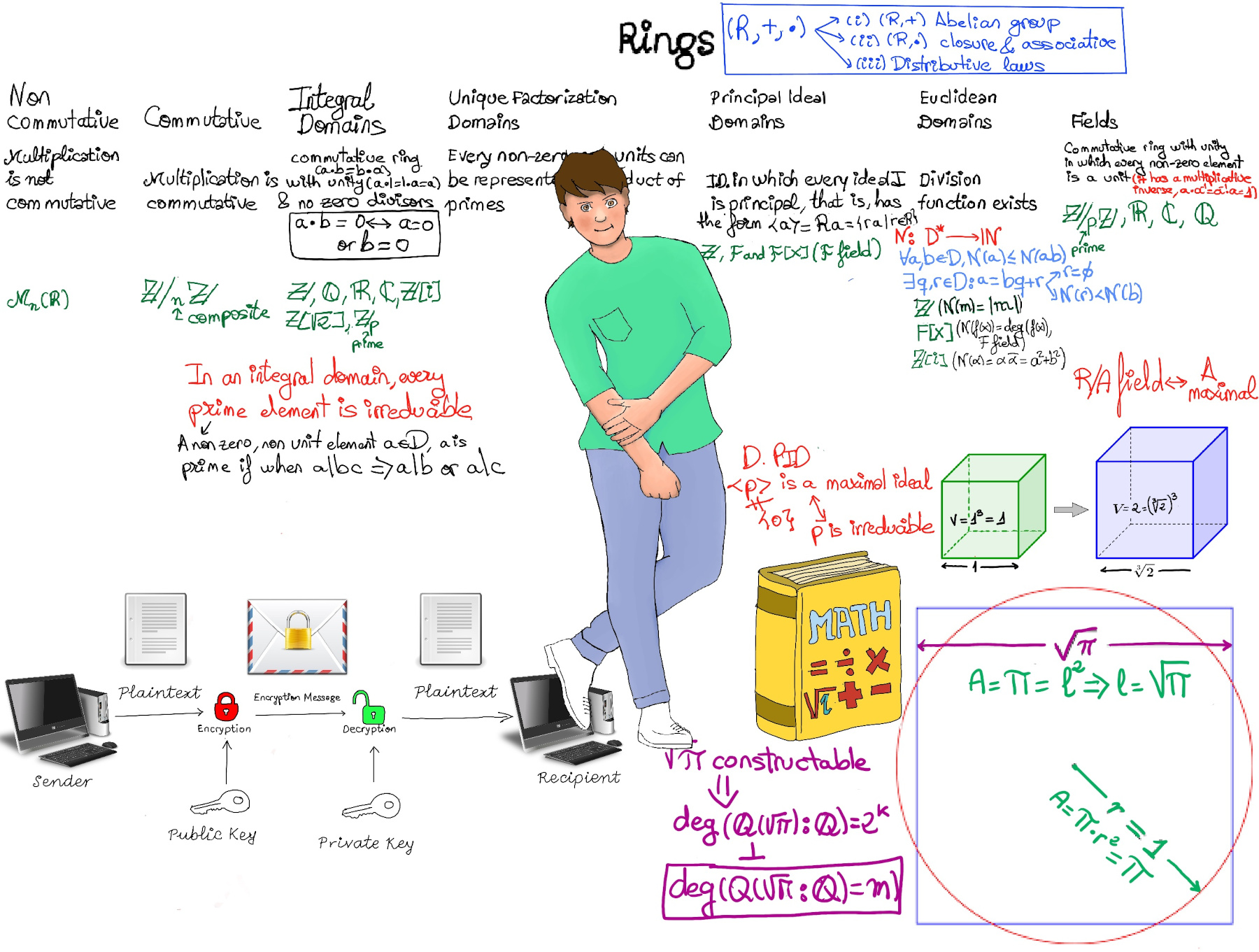
Loosely speaking, the inverse function of a function f is a function that undoes the operation of the original function. If f is a function that maps each element x in its domain to a unique element y in its codomain, then the inverse function, denoted as $f^{-1}$, maps each y back to its corresponding x.

For a given function f, its inverse g(=f^-1) is a function that reverses its result (g reverses the input and output of the original function), g(f(x))=x. An example is f(x)=$\sqrt{x},$ (x ≥ 0) g(f(x))=x ↭ g(x)= x², -1.a.- The square function (x²) is the inverse of the square root function ($\sqrt{x}$). The natural logarithm function is the inverse of the exponential function (1.e.). Logarithmic functions are the inverses of exponential functions, y = a^x, f^-1(x) = log_a(x).

If you want to plot the graph of f^-1, you just need to reflect the graph of f(x) about the line y = x.

For an inverse function to exist, the original function must be both one-to-one (injective) and onto (surjective). A function is one-to-one if each element of the domain maps to a distinct (unique) element in the codomain, and it is onto if every element in the codomain is mapped to by at least one element in the domain or, in other words, has a pre-image in the domain.

Examples

• f(x) = $\frac{2x+5}{3x-2}$. To find the inverse of a function, you need to switch the roles of x and y, and then solve for y in terms of x.

$ x = \frac{2y+5}{3y-1} ⇒ 3yx -x = 2y + 5 ⇒ y(3x-2) = x + 5 ⇒ f^{-1}(x) = \frac{x+5}{3x-2}.$

• f(x) = x³ -1. The inverse function is found by switching the roles of x and y and solving for x: x = y³ -1 ↭ y³ = x +1 ↭ $f^{-1}(x) = \sqrt[3]{x+1}$

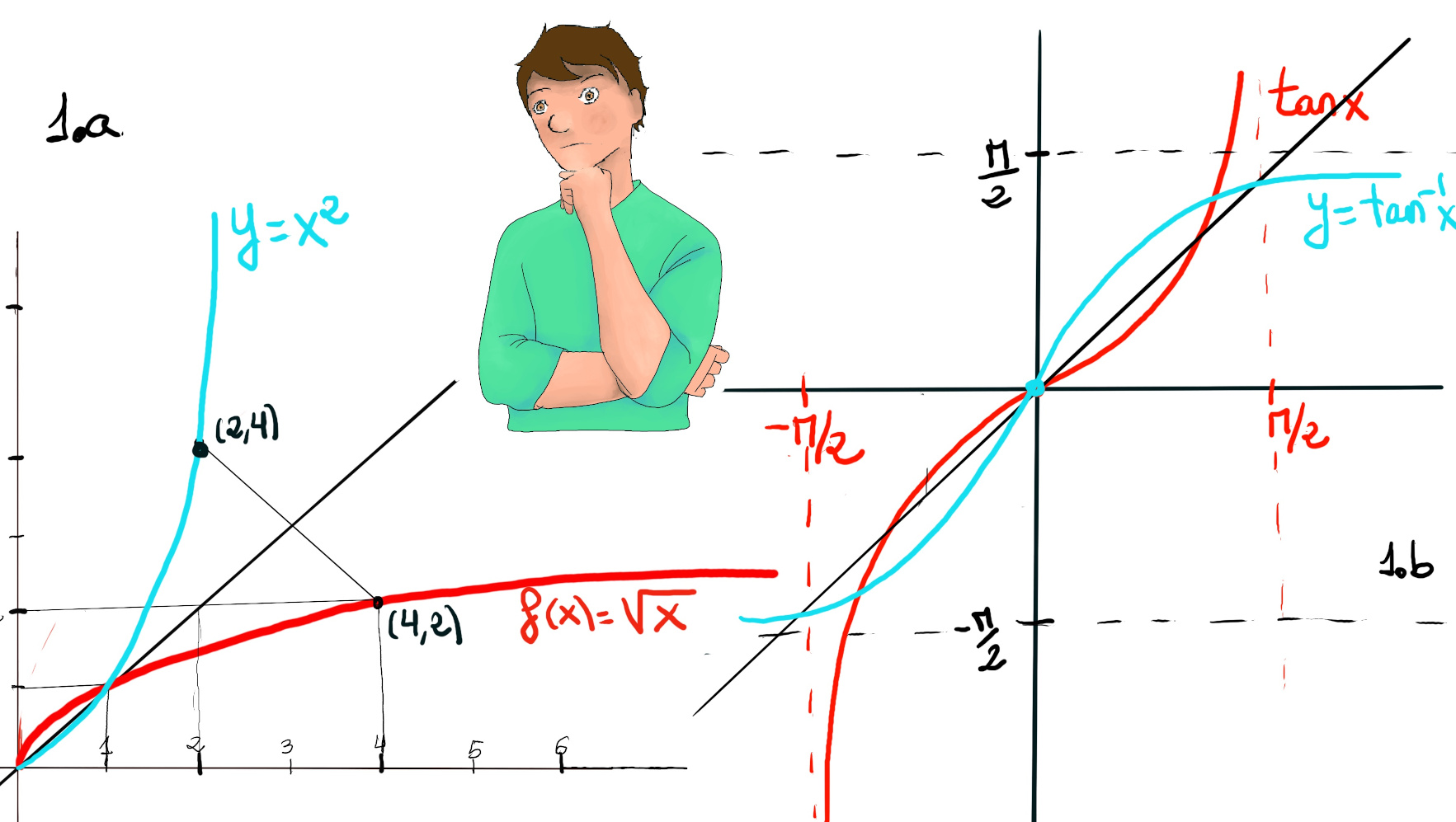
• f(x) = 2x + 3. This function is one-to-one and onto. The inverse function is found by switching the roles of x and y and solving for x: y = 2x + 3 ↭ x = ^(y-3)⁄₂ ⇒ f^-1(x) = ^(x-3)⁄₂ (Figure 1.a).

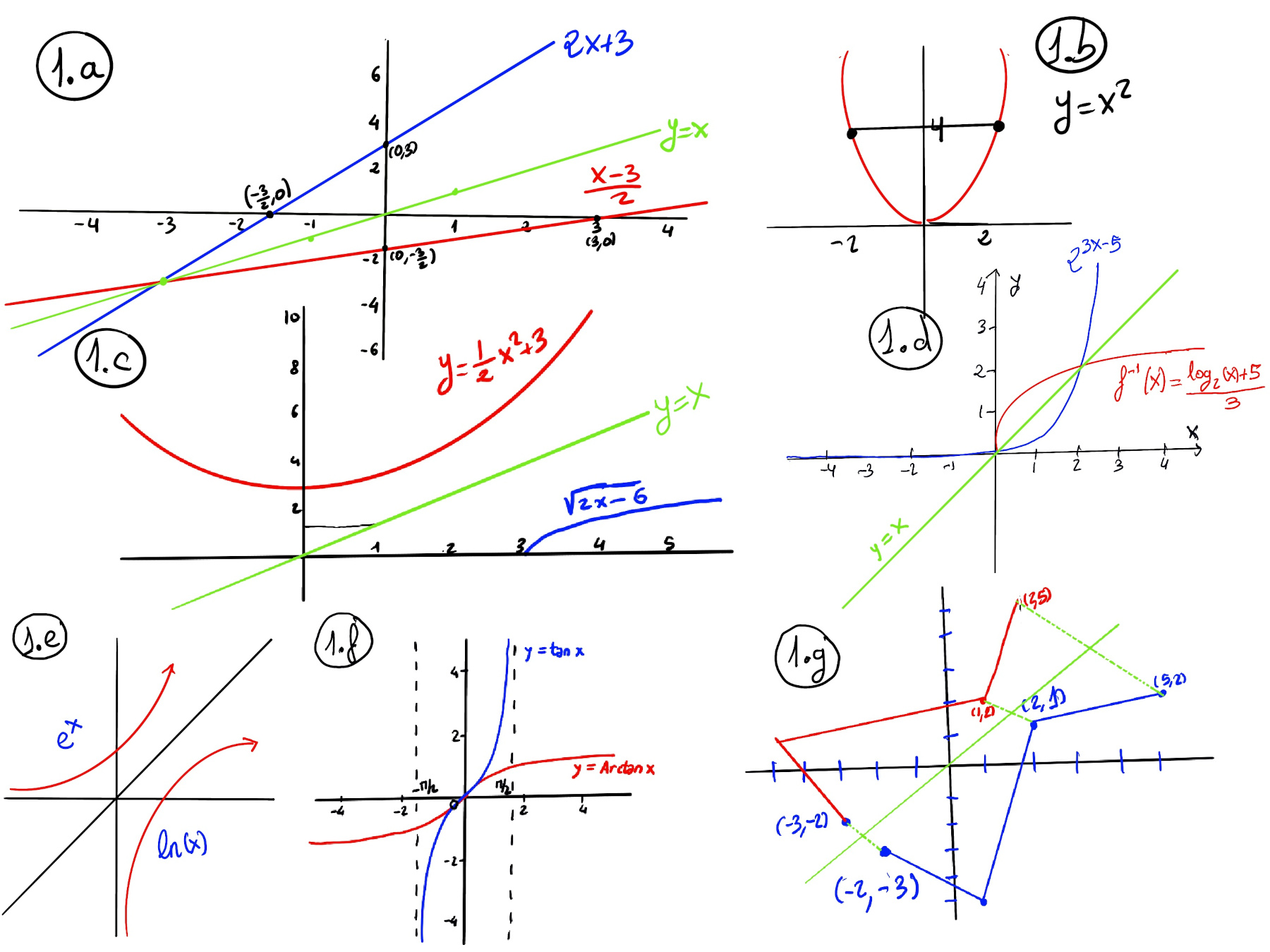
• Counterexample: f(x) = x². Since g(x) is not one-to-one (f(2) = f(-2) = 4), it does not have an inverse over ℝ (f^-1(4)?) (Figure 1.b.).

• f(x) = $\sqrt{2x -6}$. Notice that Domain(f) = [3, ∞] because 2x -6 ≥ 0, Range(f) = [0, ∞] (Figure 1.c).

y = $\sqrt{2x -6}$. To find the inverse of a function, you need to switch the roles of x and y, and then solve for y in terms of x. $x^2 = (\sqrt{2y-6})^2 ⇒ x^2 = 2y -6 ⇒ f^{-1}(x) = \frac{1}{2}x^2 + 3.$ Its domain is [0, ∞] and its range is [3, ∞].

• y = 2^3x-5. $x = 2^{3y-5}$⇒[log_b(b^a)=a] $log_2(x) = 3y -5 ⇒$ f^-1(x) = ^{(log₂(x)+5)}⁄₃ (Figure 1.d.)

• Find the inverse function based on the given graph (Figure 1.g).

• Prove that the following two functions are inverses.

To prove that two functions are inverses, one needs to show that composing one function with the other gives the identity function. In other words, if f and g are functions such that f(g(x)) = f(g(x)) = x and g(f(x)) = g(f(x))=x for all x in their respective domains, then f and g are inverses of each other.

1. f(x) = 2x +3, g(x) = $\frac{x-3}{2}$. f(g(x)) = $2\frac{x-3}{2}+3 = x -3 + 3 = x.$ g(f(x)) = $\frac{2x +3-3}{2} = \frac{2x}{2} = x$.
2. f(x) = $\sqrt{x+5}$, g(x) = x² -5. f(g(x)) = $\sqrt{x^2-5+5} = \sqrt{x} = x$. g(f(x)) = $(\sqrt{x+5})^2-5 = x +5 -5 = x$.

• Martha earns 8 dollars per hour, works a minimum of 40 hours per week, and receives overtime pay at a rate of 1.5 times her regular hourly wage. If Martha’s total earnings for last week were $380, determine the number of hours she worked (Figure vi).

1.5 times her regular hourly wage = 12.

f(x) =[Martha works a minimum of 40 hours per week] 40·8 + 12(40-x) = 320 + 12(x -40) = 12x -160.

x = 12y -160 ↭ $f^{-1}(x) = \frac{x+160}{12}$. It represents Martha’s earning for a weak, hence $f^{-1}(x) = \frac{380+160}{12} = 45$, that is, Marta worked 45 hours last week (5 extra hours).

• Trigonometric functions are not one-to-one (or even defined) over their entire domains, but we can define restricted domains to make them one-to-one and onto, e.g., sin(x) is both one-to-one and onto for 0 ≤ x ≤ π, its inverse is sin^-1(y) = arcsin(y).

• f(x) = tan(x). Arctangent is the inverse of the tangent. Tangent is the ratio of the opposite side to the adjacent side in a right triangle, and arctangent is the angle whose tangent is the argument. The restricted domain of tangent is $(-\frac{\pi}{2}, \frac{\pi}{2})$ and its codomain or range is ℝ (Figure 1.f).

Derivate of inverse functions

Theorem. Derivate of inverse functions. Given an invertible function f, the derivate of its inverse function f^-1(x) evaluated at x = a is $f^{-1'}(a)=\frac{1}{f'(f^{-1}(a))}$.

Proof.

By definition, y = f^-1(x) ↭ x = f(y)⇒[Chain Rule] $1 = f’(y)·\frac{dy}{dx}⇒ \frac{dy}{dx} = \frac{1}{f’(y)}$⇒[y = f^-1(x)] $f^{-1’}(x) = \frac{1}{f’(f^{-1}(x))}$ ⇒[x = a] $f^{-1’}(a) = \frac{1}{f’(f^{-1}(a))}$∎

Examples. f(x) = x⁵ + 2x³ +7x +1, calculate f^-1’(1). $f^{-1’}(1) = \frac{1}{f’(f^{-1}(1))} = \frac{1}{f’(f^{-1}(1))}$

f’(x) = 5x⁴ +6x² + 7 > 0 ⇒ f is strictly increasing and one-to-one. f(0) = 1 ⇒[f is one-to-one] f^-1(1) = 0 ⇒ $f^{-1’}(1) = \frac{1}{f’(f^{-1}(1))} = \frac{1}{f’(f^{-1}(1))} = \frac{1}{f’(0)} = \frac{1}{7}.$

The horizontal line test

The horizontal line test is used to determine whether a function is one-to-one when its graph is given.

1. If every horizontal line intersects the graph of a function at most once, then the function is one-to-one (injective).
2. If any horizontal line y=c intersects the graph in more than one point, the function is not injective.
3. The function is onto (i.e., surjective) if and only if its graph intersects any horizontal line at least once.
4. f is bijective if and only if any horizontal line will intersect the graph exactly once.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.