Derivate 3. Trigonometric Functions.

Trigonometry is a “sine” of the times, Anonymous.

Trigonometry is the foundation upon which calculus stands tall.

Recall

The derivative of a function at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. It is the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable.

Definition. A function f(x) is differentiable at a point “a” of its domain, if its domain contains an open interval containing “a”, and the limit $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$ exists, f’(a) = L = $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$. More formally, for every positive real number ε, there exists a positive real number δ, such that for every h satisfying 0 < |h| < δ, then |L-$\frac {f(a+h)-f(a)}{h}$|< ε.

1. Power Rule: $\frac{d}{dx}(x^n) = nx^{n-1}$.
2. Constant Multiple Rule: $\frac{d}{dx}(cf(x)) = c \cdot \frac{d}{dx}(f(x))$.
3. Sum Rule: $\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))$
4. Product Rule: $\frac{d}{dx}(f(x) \cdot g(x)) = f’(x)g(x) + f(x)g’(x)$.
5. Quotient Rule: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f’(x)g(x) - f(x)g’(x)}{(g(x))^2}$
6. Chain Rule: $\frac{d}{dx}(f(g(x))) = f’(g(x)) \cdot g’(x)$

Basic trigonometry

A triangle is a closed, 2-dimensional shape or figure with 3 sides, 3 angles, and 3 vertices. It is a three-sided polygon and the sum of its three angles equals 180°. It is one of the most basic shapes in geometry and is denoted by the symbol △.

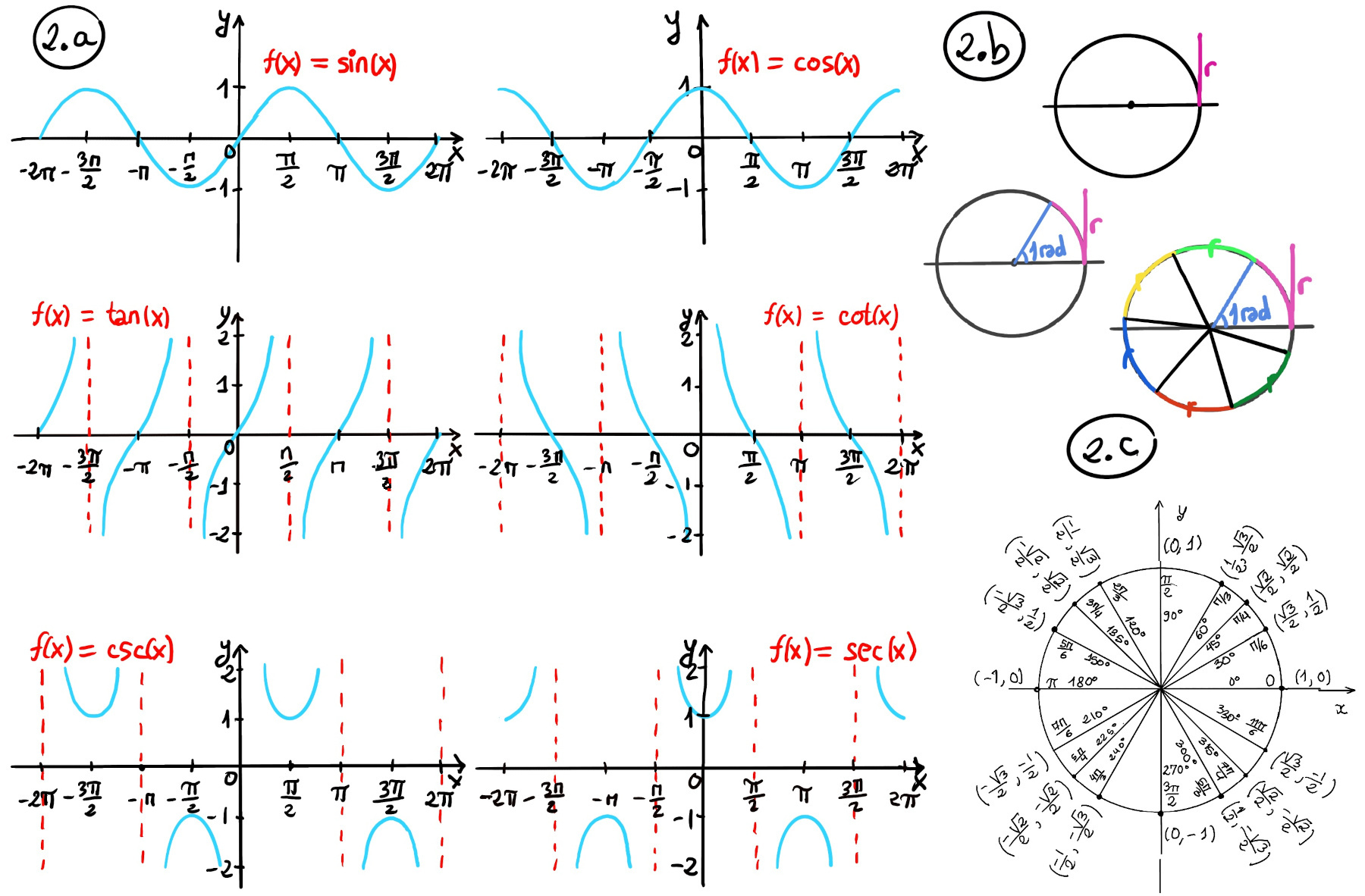
The sine function is the ratio of the length opposite to the given angle and the hypotenuse of the given triangle, $sin(θ) = \frac{opposite}{hypotenuse} = \frac{o}{h}$. It is odd (sin(-x) = -sin(x), the graph is symmetric with respect to the origin), periodic with a period of 2π, and it ranges between -1 and 1 (Figure 1.a.).

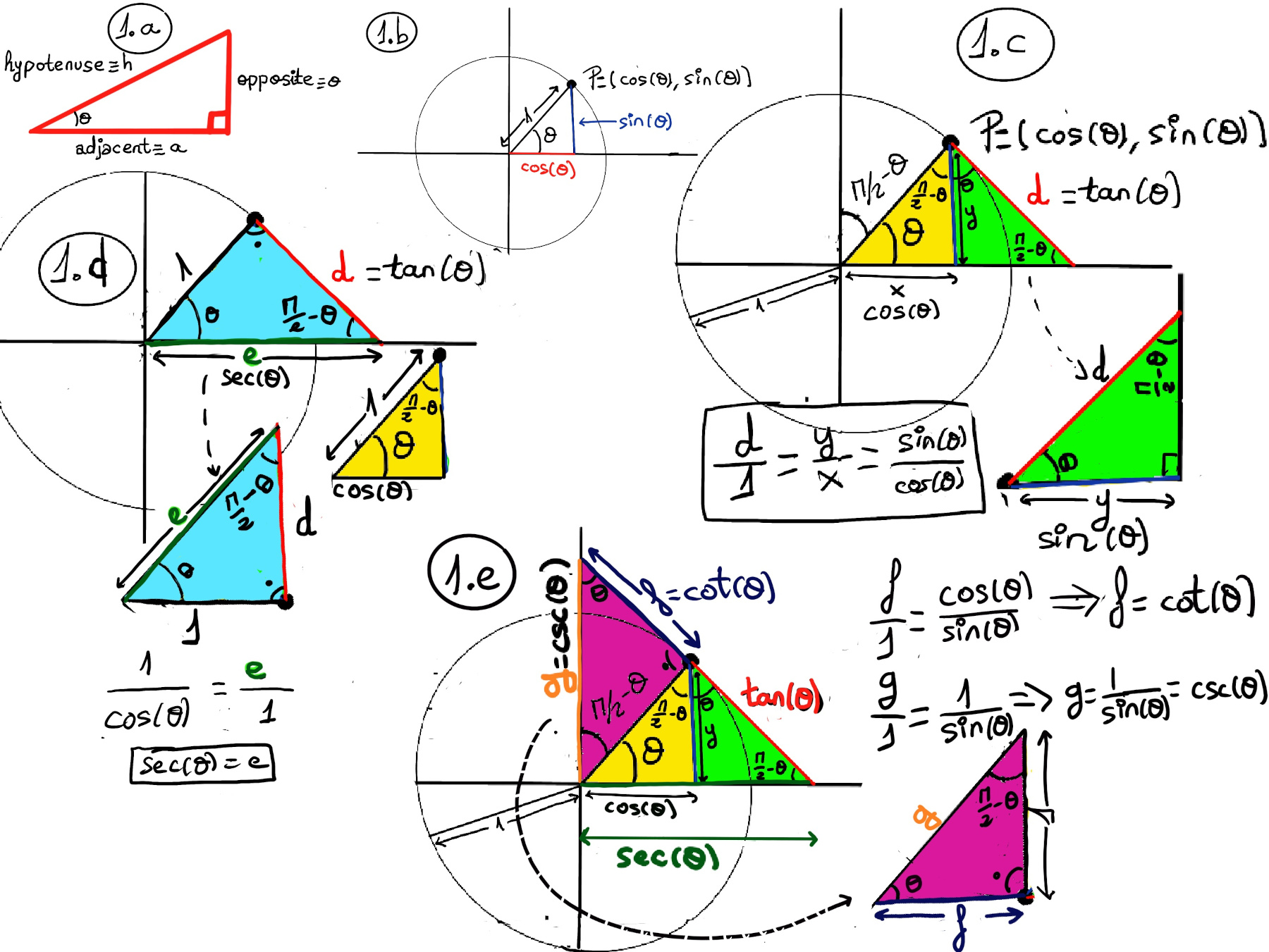
The cosine function is the ratio of the length adjacent to the given angle and the hypotenuse of the given triangle, $cos(θ) = \frac{adjacent}{hypotenuse} = \frac{a}{h}$. It is even (cos(-θ) = cos(θ), the graph is symmetric about the y- or the vertical axis), periodic with a period of 2π, and its range is between -1 and 1.

The tangent function is the ratio of the opposite side to the adjacent side, $tan(θ) = \frac{opposite}{adjacent} = \frac{o}{a}$. It is an odd function (tan(-x) = -tan(x)). The domain of the tangent function is all real numbers, except at x-values where there are vertical asymptotes, namely x = $\frac{π}{2} +nπ = \frac{(π+(nπ2))}{2} = \frac{(2n+1)π}{2}$ where n ∈ ℤ. The range of the tangent function is all real numbers.

Easy way to remember this trigonometrical ratios is with the mnemonic as SOH-CAH-TOA, meaning Sine is Opposite over the Hypotenuse, Cosine is Adjacent over the Hypotenuse, and Tangent is Opposite over the Adjacent.

Consider the unit circle, i.e., a circle with a radius of 1 unit. Denote its center (0,0) as O, and denote the point (1,0) on it as A. As a moving point B travels around the unit circle starting at A and moving in a counterclockwise direction, the angle AOB increases. When B has made it all the way around the circle and back to A, then angle AOB is a 360° angle, that is the same angle as 0°. Therefore, for any arbitrary angle θ, $sin(θ+360°) = sin(θ), cos(θ+360°) = cos(θ) ↭ sin(θ+2π) = sin(θ), cos(θ+2π) = cos(θ)$

In the unit circle, the sine function represents the y-coordinate and the cosine function represents the x-coordinate of the point, say P = (cos(θ), sin(θ)), where the terminal side of the angle intersects the circle (Figure 1.b.).

Recall that Cartesian coordinates are used to uniquely identify points in a two-dimensional plane by their distances from two perpendicular lines called the x-axis and the y-axis. The plane is divided into four quadrants based on the signs of the coordinates, namely Q1, Q2, Q3, and Q4, e.g., the upper-right quadrant where both the x and y coordinates are positive is Q1.

The complementary angle in the first quadrant Q1 to theta is $\frac{π}{2}-θ$ (yellow triangle, figure 1.c.) ⇒ $cos(θ) = sin(\frac{π}{2}-θ)$. Next, we draw a line that is tangent to the circle at P(cos(θ), sin(θ)) and perpendicular to the radius, and let’s name the line segment d, and we can observe that we have two similar triangles (yellow and green triangles are similar triangles because they have the same angles, namely $\pi, \theta, \frac{π}{2}-\theta$, figure 1.c).

Similar triangles are triangles that are the same shape but not necessarily the same size. Similar triangles are triangles whose corresponding angles are equal and whose corresponding sides are proportional but not necessarily equal.

Therefore, $\frac{d}{1} = \frac{y}{x} = \frac{sin(θ)}{cos(θ)} ⇒ d = tan(θ)$

Similarly, the blue and yellow triangles are similar (Figure 1.d) ⇒ $\frac{1}{cos(θ)} = \frac{e}{1} ⇒ sec(θ) = e.$ Recall that the secant is the reciprocal of the cosine. Finally, we draw a perpendicular line to the radius that is tangent to the circle at P and connects to the y-axis and the reader may realize that the pink and yellow triangles are similar (Figure 1.e) ⇒ $\frac{f}{cos(θ)} = \frac{1}{sin(θ)} ↭ \frac{f}{1} = \frac{cos(θ)}{sin(θ)} = cot(θ) ⇒ f = cot(θ), \frac{g}{1} = \frac{1}{sin(θ)} ⇒ g = \frac{1}{sin(θ)} = csc(θ)$. Recall that cotangent is the reciprocal of the tangent, i.e., the ratio of the adjacent side to the opposite side in a right triangle. Besides, the cosecant is the reciprocal of the sine.

By the Pythagorean theorem in the yellow triangle, we obtain that $sin^2(θ)+cos^2(θ) = 1.$ By the Pythagorean theorem in the yellow+green triangle, $1+tan^2(θ) = sec^2(θ),$ and in the pink triangle, $1+cot^2(θ) = csc^2(θ).$

Angles measurements in degrees and radians.

A radian is the angle subtended at the centre of a circle by an arc that is equal in length to the radius of the circle. The length of a circumference is given by the following expression: l =[d is the diameter] π·d = 2·π·r. If you take the circumference of a circle and divide it by its radius ($\frac{l}{r} = 2·π$), you get 2π radians (or approximately 6.28318 radians) for one complete revolution ≈ 6 rad + 0.28318 (Figure 2.b).

Besides, if you have the unit circle, an angle of π radians corresponds to halfway around the circle (180 degrees), and an angle of 2π radians corresponds to one complete revolution (360 degrees) -Figure 2.c.-, and various fractions of π corresponds to different angles, e.g., 30° is π/6, 45° is π/4, 60° is π/3, and so on.

Let’s calculate sin(30°) and cos(30°) (Figure 3.b). We draw the red triangle, and we know the opposite angle equals 60° (the three interior angles of a triangle will always have a sum of 180°). We draw, or more formally reflect, an image of our triangle along the x-axis (the skyblue triangle.) Then, we have created a new triangle with its three interior angles equals to 60° ⇒[An equiangular triangle is always equilateral.] The three sides have the same side, 1, hence sin(30°) = ¹⁄₂.

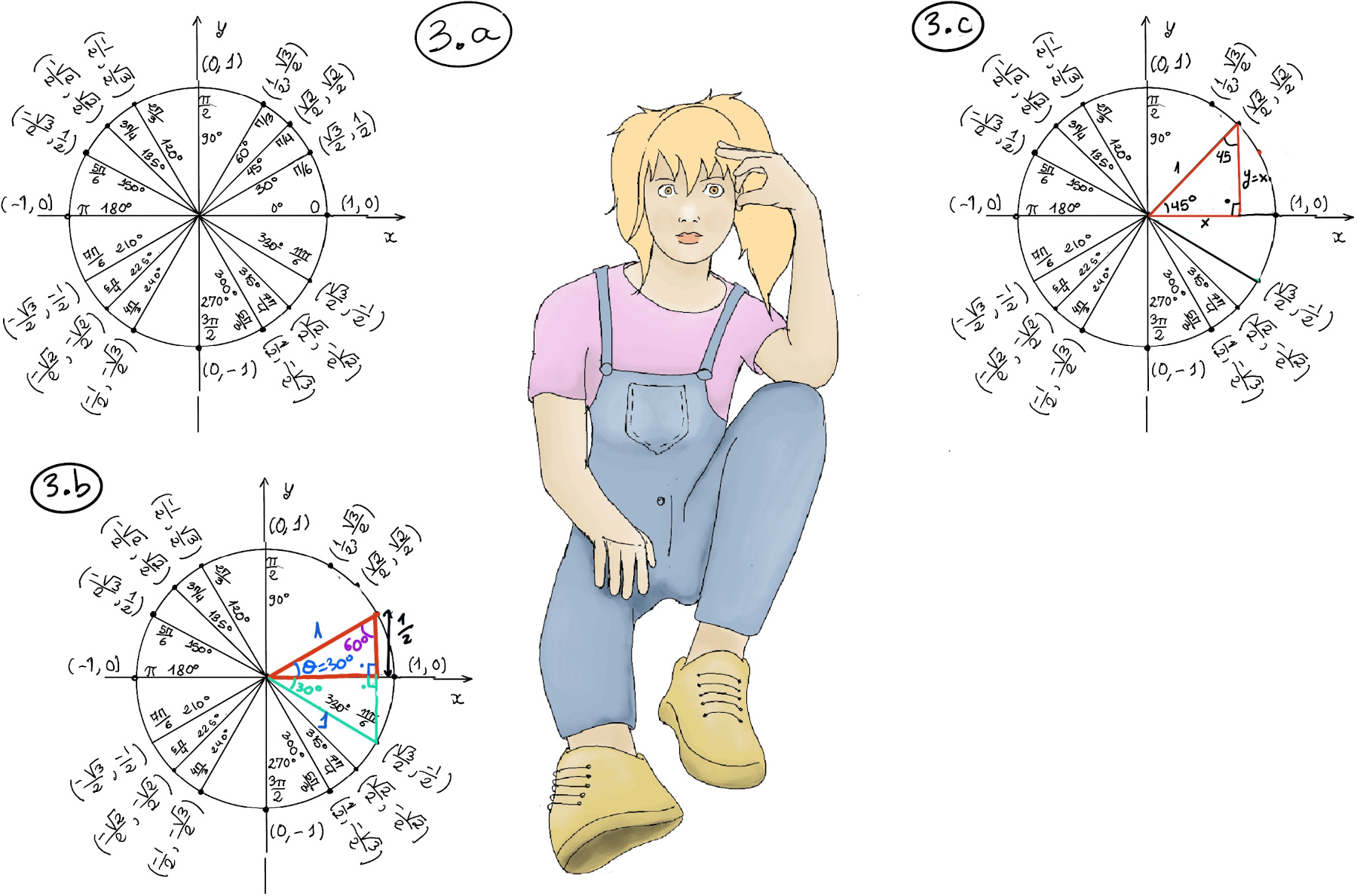
By the Pythagorean theorem, $cos^2(30)+(\frac{1}{2})^2 = 1 ⇒ cos^2(30)+\frac{1}{4} = 1 ⇒ cos^2(30) = \frac{3}{4} ⇒ cos(30) = \frac{\sqrt{3}}{2}.$

Let’s calculate sin(45°) and cos(45°) (Figure 3.c). We draw the red triangle, and we know the opposite angle equals 45° (The three interior angles of a triangle will always have a sum of 180°) ⇒ the length of the adjacent and the opposites sides are equal, and by the Pythagorean theorem $1^2 = x^2 + x^2 ⇒ 2x^2 = 1 ⇒ x = y = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} ⇒ cos(45°)=sin(45°) = \frac{\sqrt{2}}{2}.$

Common trigonometry formulas

$\textbf{Basic Trigonometric Identities:}$

$sin^2(x) + \cos^2(x) = 1, 1 + \tan^2(x) = \sec^2(x), 1 + \cot^2(x) = \csc^2(x).$

$\textbf{Angle Sum and Difference Formulas:}$

$sin(A \pm B) = \sin A \cos B \pm \cos A \sin B, \cos(A \pm B) = \cos A \cos B \mp \sin A \sin B, \tan(A \pm B) = \frac{\tan A \pm \tan B}{1 \mp \tan A \tan B}.$

$\textbf{Double Angle Formulas:}$

$\sin(2x) = 2\sin x \cos x, \cos(2x) = \cos^2 x - \sin^2 x = 1 -2\sin^2 x = 2\cos^2 x -1, \tan(2x) = \frac{2\tan x}{1 - \tan^2 x}.$

$\textbf{Half Angle Formulas:}$

$\sin\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1 - \cos x}{2}},\cos\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1 + \cos x}{2}}, \tan\left(\frac{x}{2}\right) = \frac{\sin x}{1 + \cos x}$.

$\textbf{Product-to-Sum Formulas:}$

$\sin A \sin B = \frac{1}{2} [\cos(A - B) - \cos(A + B)], \cos A \cos B = \frac{1}{2} [\cos(A - B) + \cos(A + B)], \sin A \cos B = \frac{1}{2} [\sin(A + B) + \sin(A - B)], \cos A \sin B = \frac{1}{2} [\sin(A + B) - \sin(A - B)]$

$\textbf{Sum-to-Product Formulas:}$

$\sin A + \sin B = 2\sin\left(\frac{A + B}{2}\right)\cos\left(\frac{A - B}{2}\right), \sin A - \sin B = 2\sin\left(\frac{A - B}{2}\right)\cos\left(\frac{A + B}{2}\right), \cos A + \cos B = 2\cos\left(\frac{A + B}{2}\right)\cos\left(\frac{A - B}{2}\right), \cos A - \cos B = -2\sin\left(\frac{A + B}{2}\right)\sin\left(\frac{A - B}{2}\right).$

Derivatives of Trigonometric Functions

• sin’(x)=cos(x)

$\frac{sin(x+h) -sin(x)}{h} =$ [Recall, sin(a+b) = sin(a)cos(b) + cos(a)sin(b)] $\frac{sin(x)cos(h) + cos(x)sin(h) -sin(x)}{h} = sin(x)(\frac{cos(h)-1}{h}) + cos(x)(\frac{sin(h)}{h})$

$lim_{h \to 0} \frac{sin(x+h) -sin(x)}{h} = lim_{h \to 0} sin(x)(\frac{cos(h)-1}{h}) + cos(x)(\frac{sin(h)}{h}) = $

And by Strategy in finding limits, $\lim_{x \to 0} (\frac{sin(x)}{x}) = 1$ and $\lim_{x \to 0} (\frac{1-cos(x)}{x}) = 0$ and limit laws,

$ = (-1)·0·sin(x) + cos(x)*1 = cos(x) $

• cos’(x)=-sin(x)

$\frac{cos(x+h) -cos(x)}{h} =$ [Recall, cos(a+b) = cos(a)cos(b) - sin(a)sin(b)] $\frac{cos(x)cos(h) - sin(x)sin(h) -cos(x)}{h} = cos(x)(\frac{cos(h)-1}{h}) - sin(x)(\frac{sin(h)}{h})$

And by Strategy in finding limits, $\lim_{x \to 0} (\frac{sin(x)}{x}) = 1$ and $\lim_{x \to 0} (\frac{1-cos(x)}{x}) = 0$ and limit laws,

$ = cos(x)·-1·0 -sin(x)·1 = -sin(x).$

• tan’(x) = $\frac{1}{cos^{2}x}$

$\frac{d}{dx}\frac{sinx}{cosx}$ =[Quotient Rule] $\frac{cosxcosx+sinxsinx}{cos^{2}x} = \frac{1}{cos^{2}x}$

Summary

1. Power Rule: $\frac{d}{dx}(x^n) = nx^{n-1}$.
2. Sum Rule: $\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))$
3. Product Rule: $\frac{d}{dx}(f(x) \cdot g(x)) = f’(x)g(x) + f(x)g’(x)$.
4. Quotient Rule: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f’(x)g(x) - f(x)g’(x)}{(g(x))^2}$
5. Chain Rule: $\frac{d}{dx}(f(g(x))) = f’(g(x)) \cdot g’(x)$
6. $\frac{d}{dx}(e^x) = e^x, \frac{d}{dx}(\ln(x)) = \frac{1}{x}, \frac{d}{dx}(\sin(x)) = \cos(x), \frac{d}{dx}(\cos(x)) = -\sin(x), \frac{d}{dx}(\tan(x)) = \sec^2(x), \frac{d}{dx}(\arcsin(x)) = \frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arccos(x)) = -\frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arctan(x)) = \frac{1}{1 + x^2}.$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus.
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
9. blackpenredpen.