Separable extensions

There are two ways to do great mathematics. The first is to be smarter than everybody else. The second way is to be stupider than everybody else — but persistent, Raoul Bott.

 

Let f(x) be a polynomial, f(x) = a_nxⁿ + a_n-1x^n-1 + ··· + a₁x + a₀ ∈ F[x], with degree(f(x)) = n. We have already demonstrated that there exists an extension K/F that contains all the roots of f.

Definition. If F is a field with f(x)∈ F[x] and the factorization of f(x) = c(x -α₁)^m₁(x -α₂)^m₂···(x -α_k)^m_k, m_k ≥ 1, we say that m_i is the multiplicity of the root α_i. If m_i = 1, α_i is said to be a simple root. Otherwise, if m_i ≥ 2, α_i is said to be a multiple or repeated root.

If all of the roots of f are simple, then we say that f is separable, e.g., x²-5x +6 (3 and 2 are simple roots), x² -3x +2 (1 and 2 are simple roots). On the contrary, if f has at least one multiple root, f is said to be inseparable, e.g., x⁴ -4x³ + 4x² (0 and 2 are multiple roots), (x-1)²(x - 2)²(x² +1) (1 and 2 are multiple roots, i and -i are simple roots).

The derivative of a polynomial f(x) = a_nxⁿ + a_n-1x^n-1 + ··· + a₀ = $\sum_{i=0}^n a_ix^i$, written by f’(x) is well defined for any field F in F[x]. It is defined as the polynomial na_nx^n-1 + (n-1)a_n-1x^n-2 + ··· + a₁ = $\sum_{i=1}^n ia_ix^{i-1}$ ∈ F[x] and degree(f’(x)) ≤ n-1.

Properties of the Derivate. Let f(x), g(x) ∈ F[x], a ∈ F. Then, we have the basic properties as the derivate of calculus,

1. (f(x) + g(x))’ = f’(x) + g’(x)
2. (af(x) + bg(x))’ = af’(x) + bg’(x)
3. (f(x)g(x))’ = f(x)g’(x) + g(x)f’(x)
4. ((f(g(x)))’ = f’(g(x))g’(x)

Bezout’s identity in F[x]. Let F be a field, and let f(x) and g(x) be polynomials in F[x]. If f and g are relatively prime, then there exist polynomials h(x) and k(x) in F[x] such that f(x)h(x) + g(x)k(x) = 1

Proof.

f and g are relatively prime ⇒ there is no polynomial of positive degree in F[x] that divides both f(x) and g(x).

F is a field ⇒ F[x] is a PID ⇒ [A PID is an integral domain in which every ideal is generated by a single element] So the ideal in F[x] generated by f and g, ⟨f(x), g(x)⟩ is generated by a single element, ⟨f(x), g(x)⟩ = a(x) for some a(x) ∈ F[x]. Thus a(x) divides both f(x) and g(x). This means that a(x) is a constant multiple of a unit, i.e. a constant polynomial, say a ∈ F, since these polynomials are coprime ⇒ it contains 1 (c·a ∈ ⟨f(x), g(x)⟩ for any element c ∈ F, in particular a^(-1)*a = 1), 1 ∈ ⟨f(x), g(x)⟩ and therefore there exist polynomials h(x) and k(x) in F[x] such that f(x)h(x) + g(x)k(x) = 1∎

Alternative definition. Let K be a splitting field of a polynomial f(x) ∈ F[x]. Let α be a root of this polynomial f(x), then (x -α) would be a factor of f(x), that is, (x - α) divides f(x) in K[x]. If (x - α)^s divides f(x) in K[x], s > 1, α is a multiple root of f(x).

Theorem. Criterion for multiple zeros. Let f(x) be a polynomial over a field F (f(x) ∈ F[x]), f(x) has a multiple zero a (root with multiplicity greater than 1) in some extension E of F iff f(x) and f'(x) have a common factor of positive degree in F[x] ↭ f(a) = f’(a) = 0.

Example. f(x) = x² -4x + 4. f(2) = 0, 2 is a zero of f(x) with multiplicity 2. f’(x) = 2x -4, f’(2) = 0. Notice that (x -2) is a common factor of f(x) and f’(x) because f(x) = (x -2)² and f’(x) = 2(x -2).

Proof.

⇒) Let f(x) has a multiple zero “a” in some extension E/F ⇒ ∃g(x)∈E[x]: f(x) = (x -a)²g(x).

f’(x) = [Properties of the Derivate] (x -a)²g’(x) + 2(x -a)g(x) = (x -a)·[(x -a)g’(x) + 2g(x)] ⇒ (x -a) is a factor of both f(x) and f’(x) in some extension E of F ⇒ [Factor Theorem. A polynomial f(x) has a factor (x -α) if and only if α is a root, i.e., f(α) = 0.] f(a) = f’(a) = 0.

⇐) Suppose that f(x) and f’(x) have a common factor of positive degree (x -a) ↭ [Factor Theorem] Let a be a zero of the common factor, f(a) = f’(a) = 0.

a is a zero of f(x) ↭ (x - a) divides f(x) ⇒ ∃q(x): f(x) = (x -a)q(x). Then, f’(x) = (x -a)q’(x) + q(x) ⇒ 0 = f’(a) = q(a) ⇒ q(a) = 0 and x -a is a factor of q(x) and [f(x) = (x -a)q(x)] f(x) is divisible by (x -a)² ⇒ “a” is a multiple zero of f(x).

Definition. A field F is called perfect if either has characteristic zero or when F has characteristic p > 0, every element of F is a pth power, i.e., F^p = {a^p | a ∈ F} = F. ↭ Every irreducible polynomial over F is separable (has distinct roots), e.g., ℚ, ℂ, and $\mathbb{F_q}$. In particular, all fields of characteristic zero and all finite fields are perfect.

In a field K with characteristic p, the Frobenius map x → x^p is a field homomorphism. Indeed, $(x + y)=\sum_{k=0}^p{p \choose k}x^py^{p-k} = x^p+y^p$ because all the intermediate terms are zero ($p | {p \choose k}$). A field homomorphism is necessarily injective, because ker(Φ) is a proper ideal of K, hence it is {0} or K (it would be the identity⊥).

If K = $\mathbb{F_p}$, i.e., a finite field, then the Frobenius map is surjective, because an injective function from a finite set to itself must be surjective. However, in a field such as K = $\mathbb{F_p(t)}$={$\frac{f}{g}| f, g ∈ \mathbb{F_p(t)},g ≠ 0$}, the field of rational functions with coefficients in the field with p elements, the Frobenius map is not surjective, e.g., t is not in the image of Φ, suppose $Φ(\frac{f}{g})=\frac{f^p}{g^p}=t ⇒$ p·(deg(f) - deg(g)) = deg(t) = 1 ⊥ def(f) - deg(g) is an integer and 1 is not divisible by p.

Recall. Freshman’s Dream or Exponentiation. Let R be a commutative ring with unity of characteristic p. Then, (a + b)^p=a^p + b^p

Theorem. Every finite field is perfect.

Proof.

Suppose that F has characteristic p, then we claim that Φ: F → F defined by Φ(x) = x^p (the Frobenius endomorphism) is a field isomorphism or automorphism.

1. Φ(a +b) = (a +b)^p = [Freshman’s Dream or Exponentiation. For completeness’ sake, we repeat the argument] $a^p+(\begin{smallmatrix}p\\1\end{smallmatrix})a^{p-1}b+(\begin{smallmatrix}p\\2\end{smallmatrix})a^{p-2}b^2+···+(\begin{smallmatrix}p\\p-1\end{smallmatrix})ab^{p-1}+b^p = a^p+b^p$ = Φ(a)+Φ(b) because all other terms cancel. Notice that $(\begin{smallmatrix}p\\i\end{smallmatrix})=\frac{p!}{i!(p-i)!}$ are integers divisible by p (there is a p in the numerator, but not in the denominator and p is prime).
2. Φ(ab) = (ab)^p=a^pb^p = Φ(a)Φ(b).
3. Φ(a) = Φ(b) ⇒ a^p = b^p ⇒ [Φ distributes over addition and (-1)^p = -1 in $\mathbb{F_p}$ for any prime p] (a -b)^p = 0 ⇒ [F is a field] a - b = 0 ⇒ a = b, Φ is injective.
4. Φ is one-to-one homomorphism, and F is finite ⇒ Φ is onto ⇒ F^p = F.

Proposition. Let F be any field.

1. An irreducible polynomial f ∈ F[x] is separable iff the greatest common factor of f and f' is 1, it is expressed or written as (f, f') = 1, f is relatively prime to its derivate.
2. If F has characteristic zero, F is a finite field or perfect, then every polynomial in F[x] is separable.
3. If F has characteristic zero, F is a finite field or perfect, then any finite extension K/F is separable.

Proof.

Let K be a finite extension of F where both f and f’ split completely (e.g., let K be the splitting field of the polynomial f·f’), then (f, f’)= 1 ↭ [Criterion for multiple zeros.] f and f’ have no common roots in K.

(1) Suppose a ∈ K is a root of f ⇒ f(x) = (x -a)g(x) in K[x] ⇒ f’(x) = (x-a)g’(x) + g(x)

a ∈ K is a multiple root of f ↭ (x -a)² divides f ↭ [f(x) = (x -a)g(x)] (x -a) divides g(x) ↭ (x -a) divides f’ ↭ a is a root of f'

f is separable ↭ [By definition] f does not have multiple roots in K ↭ f and f’ have no common roots in K ↭ [Criterion for multiple zeros] f and f’ are coprime in F[x]

(2) Let f be irreducible.

f is not separable ⇒ [An irreducible polynomial f ∈ F[x] is separable iff the greatest common factor of f and f' is 1, it is expressed or written as (f, f') = 1. ] (f, f’) ≠ 1 ⇒ ∃h: h = (f, f’), deg(h) > 0, h divides f and f’. Since f is irreducible, only 1 and f are possible ⇒ [deg(h)>0] h = f

Futhermore, since h divides f’, we are left with two options, f’ = 0 or deg(f’) ≥ deg(f) = deg(h) ⇒ [Differentiating a polynomial reduces the degree, deg(f’)< deg(f)] f’ = 0. In summary, for any field F, f ∈ F[x], f irreducible and not separable ⇒ f' = 0.

Example: F = $\mathbb{F_2}(t)$, f(x) = x² -t ∈ F[x] is not separable ⇒ f’(x) = 2x = [char(F)=2] 0.

There are two options:

1. If char(F) = 0, f = a_nxⁿ + a^n-1x^n-1 + ··· + a₀ ⇒ [n > 0 (f is irreducible so f cannot be constant -constants are units, so they cannot be irreducibles-), and a_n ≠ 0 ] na_n ≠ 0 ⇒ f’ = a_nnx^n-1 +a^n-1(n-1)x^n-2 + ··· + a₁x = $\sum_{i=1}^n ia_ix^{i-1}$ ≠ 0 ⇒ every irreducible polynomial over a characteristic zero field is separable.

   Alternatively, f’(x) = 0 only when ia_i = 0, i = 1, 2, ···, n ⇒ [char(F) = 0] a_i = 0, i = 1, 2, ···, n ⇒ f(x) = a₀, f is a constant, so it is not an irreducible polynomial over a field ⊥. Therefore, f(x) has no multiples zeros ↭ f and f’ are relatively prime ↭ f is separable.

2. Let’s suppose F is finite, char(F) = 0, or char(F) = p and every element of F is a pth power of some other element ⇒ The Frobenius map F → F, α → α^p is surjective (∀β ∈ F, ∃α ∈ F: α^p = β, i.e., α is a pth root of β) or, in other words, every element of F has a pth root.

f = a_nxⁿ + a^n-1x^n-1 + ··· + a₀, n > 0, aⁿ ≠ 0

Suppose f’ = a_nnx^n-1 +a^n-1(n-1)x^n-2 + ··· + a₁x = 0 ⇒ naⁿ = (n-1)a^n-1 = ··· = a¹ = 0

[(a_ixⁱ)’=(ia_ix^i-1)] If a_i≠0, then i = 0 in F ⇒ [char(F) = p] p divides i, e.g., char(F)=3, a₁₅x¹⁵ + a₁₂x¹² + a₉x⁹ + ··· + a₃x³ + a₀

Therefore, f must be of the form f = a_nx^pb_n + a_n-1x^pb_n-1 + ··· + a₁x^pb₁ + a₀ ⇒ [The Frobenius map is surjective, ∀β ∈ F, ∃α ∈ F: α^p = β, let’s take a’_i: (a_i’)^p = a_i] f = $(a_n^‘x^{b_n})^{p}+(a_{n-1}^‘x^{b_{n-1}})^{p}+···+(a_{1}^‘x^{b_{1}})^{p}+(a’_0)^p$ = [···]

Consider Char(F) = p & the Binomial Theorem, $(a+b)^n = \sum_{k=0}^{n} {n \choose k} a^{n-k}b^k$ where ${n \choose k}$ denotes the binomial coefficient, which is given by: ${n \choose k} = \frac{n!}{k!(n-k)!}$

[···] = $(a_n^‘x^{b_n}+a_{n-1}^‘x^{b_{n-1}}+···+a_{1}^‘x^{b_{1}}+a’_0)^p = (g(x))^p$

Therefore, f(x) = (g(x))^p where $g(x)=a_n^‘x^{b_n}+a_{n-1}^‘x^{b_{n-1}}+···+a_{1}^‘x^{b_{1}}+a’_0$, i.e., f cannot be irreducible ⊥.

(3) If F has characteristic zero, F is a finite field or perfect, then any finite extension K/F is separable.

∀ α ∈ K, let p(x) be its irreducible polynomial ⇒ [Char(F) = 0, F is a finite field or perfect, by (2)] p(x) is separable ⇒ K/F is separable. ∎

Theorem. If f(x) ∈ F[x] is irreducible over F, then all roots of f(x) have the same multiplicity.

Proof.

Let $\bar F$ be the algebraic closure of F. Let α and β be the roots of f(x) in $\bar F$ with multiplicity k and k’ respectively. We already know that $F(α)≈\frac{F[x]}{⟨f(x)⟩}≈F(β)$

Let’s define the isomorphism σ: F(α) → F(β), it is better understood from g(α) → g(x) + ⟨f(x)⟩ → g(β). More specifically, let a₀ + a₁α + ··· + a_nαⁿ ∈ F(α) → a₀ + a₁x + ··· + a_nxⁿ → a₀ + a₁β + ··· + a_nβⁿ, Figure 2.b.  

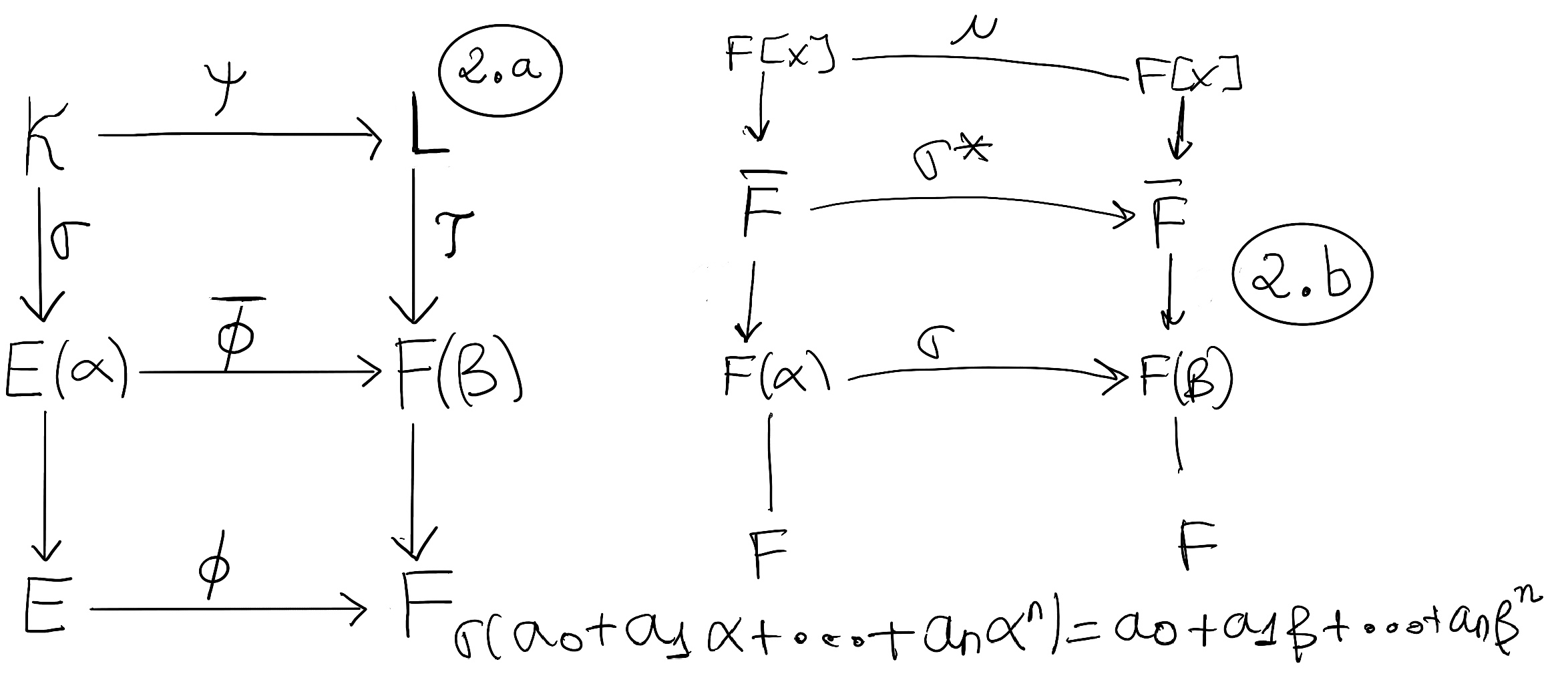
σ: F(α) → F(β), σ(α) = β is a mapping that is homomorphism, one-to-one, and onto. σ can be extended to an isomorphism σ* from $\bar F$ → $\bar F$ which induces a ring homomorphism μ: $\overline {F[x]} → \overline {F[x]}$ given by μ(a₀ + a₁x + ··· + a_rx^r) = σ*(a₀) + σ*(a₁)x + ··· + σ*(a_r)x^r

μ acts as the identity on f(x), i.e., μ(f(x)) = f(x) ⇒ μ(x -α)^k = [σ(α) = β] (x- β)^k, then f(x) = (x- β)^k··· ⇒ k ≤ k’ (k’ is β multiplicity). Mutatis mutandis, the same reasoning applies to beta respect to α ⇒ k’ ≤ k ⇒ k = k’.

Corollary. If f(x) ∈ F[x] is irreducible over F, then f(x) = a$\prod_{i=1}^r (x-α_i)^k$ where α_i are the roots of f(x) in the splitting field over F, and k is the multiplicity of each and every root.

Proof. Let f(x) be irreducible polynomial over F. Let α₁, α₂, ···, α_r be the roots of f(x). If α₁ has multiplicity k ⇒ α_i have multiplicity k ∀i, 1 ≤ i ≤ r ⇒ f(x) = a (x - α₁)^k(x - α₂)^k ··· (x - α_r)^k = a$\prod_{i=1}^r (x-α_i)^k$∎