Weighted Average II

Oddly enough most people think they are better than average.

Recall

Antiderivatives are fundamental concepts in calculus. They are the inverse operation of derivatives.

Given a function f(x), an antiderivative, also known as indefinite integral, F, is the function that can be differentiated to obtain the original function, that is, F’ = f, e.g., 3x² -1 is the antiderivative of x³ -x +7 because $\frac{d}{dx} (x^3-x+7) = 3x^2 -1$. Symbolically, we write F(x) = $\int f(x)dx$.

The process of finding antiderivatives is called integration.

The Fundamental Theorem of Calculus states roughly that the integral of a function f over an interval is equal to the change of any antiderivate F (F'(x) = f(x)) between the ends of the interval, i.e., $\int_{a}^{b} f(x)dx = F(b)-F(a)=F(x) \bigg|_{a}^{b}$

Definition. The average value of a continuous function f(x) over the interval [a, b] is AVG = $\frac{y_1+y_2+···+y_n}{n}$ where y₁, y₂, ···, y_n represent the function values at specific points within the interval [a, b] and n is the total number of points where the function is evaluated within the interval [a, b].

Since integrals are essentially a sum of all of the possible f(x) values, AVG = $\frac{1}{b-a}\int_{a}^{b} f(x)dx$.

Said in a more mathematical way, $\lim_{n \to ∞}\frac{y_1+y_2+···+y_n}{n}$ = $\frac{1}{b-a}\int_{a}^{b} f(x)dx$ where $\int_{a}^{b} f(x)dx$ represents the signed area under the curve of f(x) between x = a and x = b, and $\frac{1}{b-a}$ is a scaling factor.

The weighted average of a list of elements x₁, ···, x_n with corresponding weights w₁, ···, w_n is $\frac{w_1x_1+w_2x_2 + ··· + w_nx_n}{w_1 + ··· + w_n}$. Note that if the weights are all just 1, that is, all elements or data points have the same importance, then the weighted average is just a plain average.

The continuous analogue of a weighted average can be obtained as an integral. Let f be a function defined on an interval [a, b], with weight w(x), a non-negative function on [a, b]. Then, the formula for calculating a weighted average of f on the interval [a, b] is $\frac{\int_{a}^{b} f(x)w(x)dx}{\int_{a}^{b} w(x)dx}$, e.g., f(x) = c ⇒ $\frac{\int_{a}^{b} f(x)w(x)dx}{\int_{a}^{b} w(x)dx} = \frac{c\int_{a}^{b} w(x)dx}{\int_{a}^{b} w(x)dx} = c$.

Solved exercises

• A cylindrical metal pipe (r = 5cm, height = 20 cm) has a hot fluid flowing through it and its temperature is 90°. It is situated in the middle of a cylinder (height = 20cm, r = 15 cm) and the temperature diminishes as we move further from the center from 90° to 23°, what is the weighted temperature average? (Figure 3)

Average = $\frac{\int_{a}^{b} f(x)w(x)dx}{\int_{a}^{b} w(x)dx} = \frac{\int_{5}^{15} 2πxhw(x)dx}{\int_{5}^{15} 2πxhdx} = \frac{\int_{5}^{15} 2πxhw(x)dx}{\int_{5}^{15} 2πxhdx}$

The equation of the line passing through two points (x₁, y₁) and (x₂, y₂) is $y -y_1 = \frac{y_2-y_1}{x_2-x_1}(x-x_1)$ ⇒ The line that crosses between (5, 90) and (15, 23) is $T-90=\frac{23-90}{15-5}(x-5) ↭ T -90 = \frac{-67}{10}(x-5)↭ 10T -900 = -67x+335 ⇒ T = \frac{1235}{10}-\frac{67}{10}x$

Average = $\frac{\int_{5}^{15} 2πxhdxw(x)dx}{\int_{5}^{15} 2πxhdx} = \frac{2πh\int_{5}^{15} x(\frac{1235}{10}-\frac{67}{10}x)dx}{2πh\int_{5}^{15} xdx} = \frac{\int_{5}^{15} x(\frac{1235}{10}-\frac{67}{10}x)dx}{\int_{5}^{15} xdx} = \frac{\int_{5}^{15} (\frac{1235}{10}x-\frac{67}{10}x^2)dx}{\int_{5}^{15} xdx} = \frac{\frac{1235}{20}x^2-\frac{67}{30}x^3dx}{\frac{x^2}{2}dx}\bigg|_{5}^{15} = \frac{(13893.75-7537.5)-(1543.75-279.17)}{112.5-12.5} = \frac{6356.25−1264.58}{100} = \frac{5091.67}{100} = 50.91°C$

• Let’s select a point at random in 0 < y < 1 -x², x ∈ [-1, 1]. What ares the probabilities (or loosely speaking, the chances) x ≥ 1/2 and $\frac{-1}{2}≤x≤\frac{-1}{2}$?

$Probability(x > 1/2)$ =[PART/WHOLE] $\frac{\int_{\frac{1}{2}}^{1} (1-x^2)dx}{\int_{-1}^{1} (1-x^2)dx}$ where w(x) = 1 -x² -Figure 1.d.-. $\int_{\frac{1}{2}}^{1} (1-x^2)dx = (x-\frac{x^3}{3})\bigg|_{\frac{1}{2}}^{1} = (1-\frac{1}{3})-(\frac{1}{2}-\frac{1}{24}) = \frac{2}{3} -(\frac{12}{24}-\frac{1}{24})= \frac{16}{24}-\frac{11}{24} = \frac{5}{24}$.

$\int_{-1}^{1} (1-x^2)dx = (x-\frac{x^3}{3})\bigg|_{-1}^{1} = (1-\frac{1}{3})-(-1+\frac{1}{3}) = \frac{2}{3}-\frac{-2}{3} = \frac{4}{3}$.

$Probability(x > 1/2)$ =$\frac{\int_{\frac{1}{2}}^{1} (1-x^2)dx}{\int_{-1}^{1} (1-x^2)dx} = \frac{5}{24}:\frac{4}{3} = \frac{15}{96} = \frac{5}{32}$.

In general, a ≤ x₁ < x₂ ≤ b, P(x₁ < x < x₂) = $\frac{\int_{x_1}^{x_2} w(x)dx}{\int_{a}^{b} w(x)dx}$

Besides, p($\frac{-1}{2}≤x≤\frac{-1}{4}$) = $\frac{\int_{\frac{-1}{2}}^{\frac{-1}{4}} (1-x^2)dx}{\int_{-1}^{1}(1-x^2)dx}$ =[By symmetry] $\frac{\int_{\frac{1}{4}}^{\frac{1}{2}} (1-x^2)dx}{\int_{-1}^{1}(1-x^2)dx}$

$\int_{\frac{1}{4}}^{\frac{1}{2}} (1-x^2)dx = x-\frac{x^3}{3}\bigg|_{\frac{1}{4}}^{\frac{1}{2}} = \frac{1}{2}-\frac{1}{8}:3-(\frac{1}{4}-\frac{1}{64}:3) = \frac{12}{24}-\frac{1}{24}-(\frac{48}{192}-\frac{1}{192}) = \frac{11}{24}-\frac{47}{192} = \frac{88}{192}-\frac{47}{192} = \frac{41}{192}$

$\int_{-1}^{1} (1-x^2)dx = x-\frac{x^3}{3}\bigg|_{-1}^{1} = \frac{4}{3}$

p($\frac{-1}{2}≤x≤\frac{-1}{2}$) = $\frac{41}{192}:\frac{4}{3} = \frac{123}{768} = \frac{41}{256} ≈0.16$

• What is the possibility when we hit the golf ball aiming at a certain target, say the flag stick, the ball lands within the circular region r₂ and r₁ around the flag stick? (Figure 4)

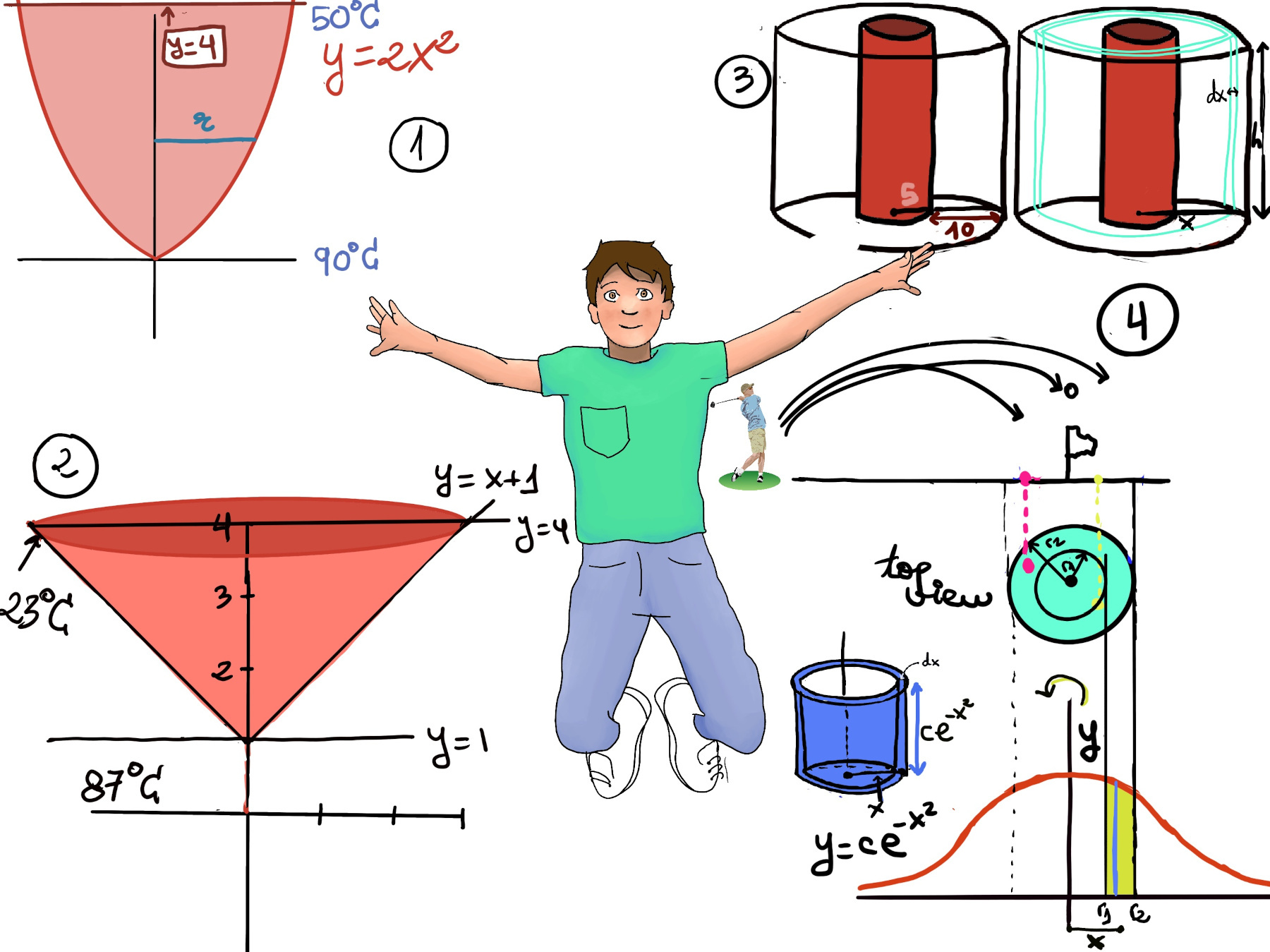
First, let’s assume something about the golfer aim, #Number of hits = ce^-x² where c is a constant representing the peak of the bell-shaped curve and x is the radial distance from the center of the flag stick to the golfer. It states that the locations where the golfer hits are normally distributed and follow a bell shape curve around the center of the flag stick.

p(r₁ < x < r₂) = $\frac{part}{whole}$

To calculate the part consider that we are integrating over cylinders of radius x, heights ce^-x², and volumes 2πx·dx·ce^-x² and we integrate from r₁ to r₂.

p(r₁ < x < r₂) = $\frac{part}{whole} = \frac{\int_{r_1}^{r_2} 2πx·ce^{-x^2}dx}{\int_{0}^{∞} 2πx·ce^{-x^2}dx}= \frac{πc\int_{r_1}^{r_2} 2xe^{-x^2}dx}{πc\int_{0}^{∞} 2xe^{-x^2}dx}$.

$part = πc(-e^{-x^2})\bigg|_{r_1}^{r_2}= πc(-e^{-r_2^2}-(-e^{-r_1^2})) = πc(e^{-r_1^2}-e^{-r_2^2})$

$whole = πc(-e^{-x^2})\bigg|_{0}^{∞}= πc(-e^{-∞^2}-(-e^{0^2})) = πc(0+1)= πc$

p(r₁ < x < r₂) = $\frac{part}{whole} =\frac{πc(e^{-r_1^2}-e^{-r_2^2})}{πc} = e^{-r_1^2}-e^{-r_2^2}.$

Notice that $\frac{d}{dx}(-e^{-x^2}) = -e^{-x^2}·(-2x)=2xe^{-x^2}$

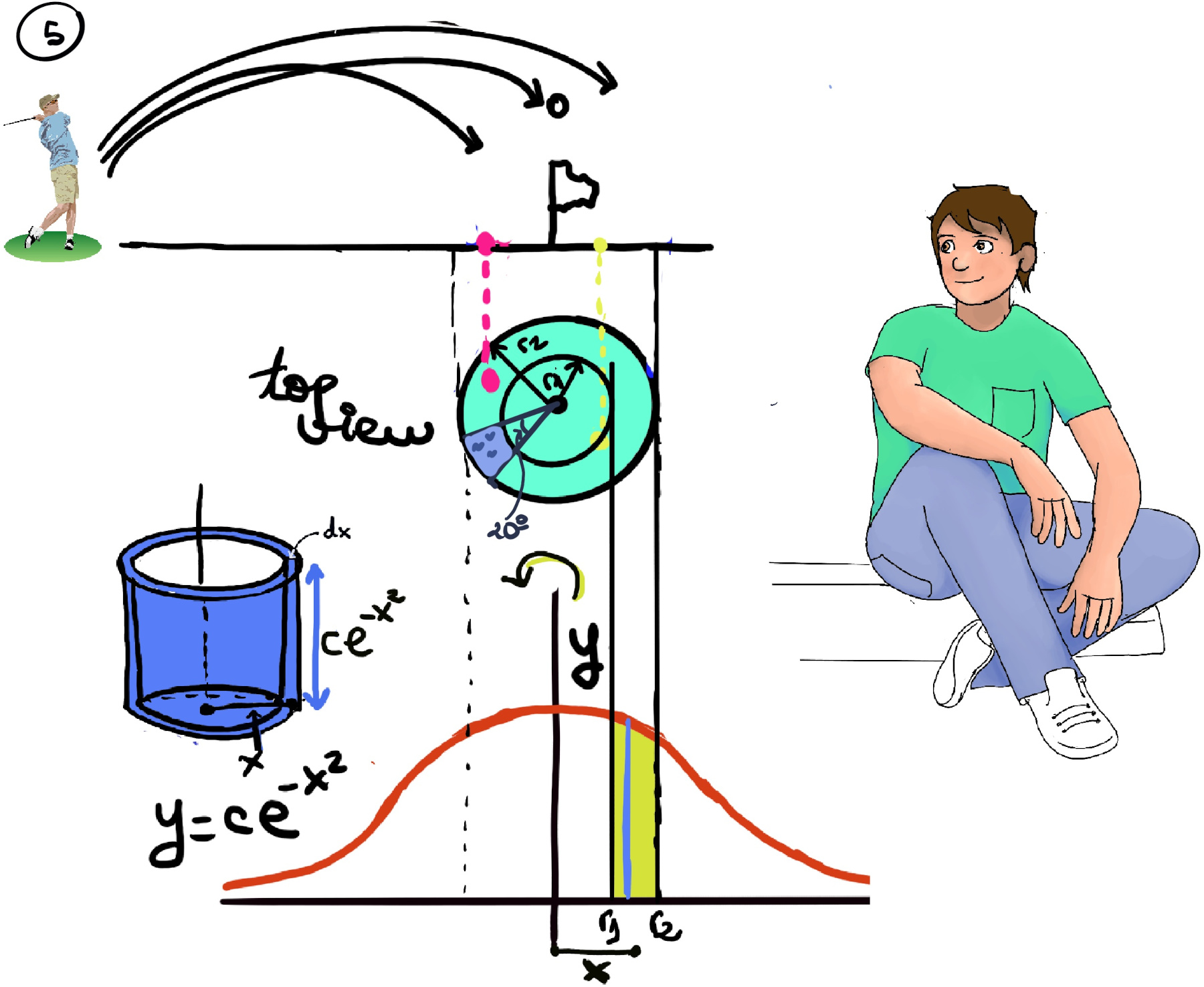• What is the possibility when we hit the golf ball aiming at the flag stick, the ball lands in the pond? (Figure 5)   p(the_ball_lands_in_the_pond) = $\frac{part}{whole}$

part = $\frac{\int_{r_1}^{r_2} 2πx·ce^{-x^2}dx}{360}*20 = \frac{20}{360}πc(e^{-r_1^2}-e^{-r_2^2}) = \frac{1}{18}πc(e^{-r_1^2}-e^{-r_2^2})$

p(the_ball_lands_in_the_pond) = $\frac{part}{whole} = \frac{\frac{1}{18}πc(e^{-r_1^2}-e^{-r_2^2})}{πc} = \frac{1}{18}(e^{-r_1^2}-e^{-r_2^2})$

• Based on MIT OpenCourseWare, Single Variable Calculus and YouTube’s Chau Tu channel. Suppose a youngster is throwing darts at a dartboard while his little brother is standing nearby. What is the probability that the brother gets hit by a dart?

First, let’s assume something about the youngster aim completely analogous to the previous exercise. #Number of hits = ce^-r². It states that the locations our youngster hits are normally distributed and follow a bell shape curve about the center of the dart board. He’s more likely to hit the dart board, but there’s some chance he’ll hit the wall next to it, or even worse his little brother.

As a general rule of thumb, we need to compute the probability of something by finding the ratio of the part to the whole. In our particular example, the “part” will be where the brother is and the “whole” is all the possible places, no matter how improbable, the dart could hit.

Let us consider a ring of the dart board. The inside of the ring will have radius r₁ and the outside will have radius r₂. If we plot y = e^-r², we get a “side view” of our probability distribution where the heigh indicate that the darts are most likely to land near the center of the dartboard and less likely to land far out from the center -Figure 1.a-.

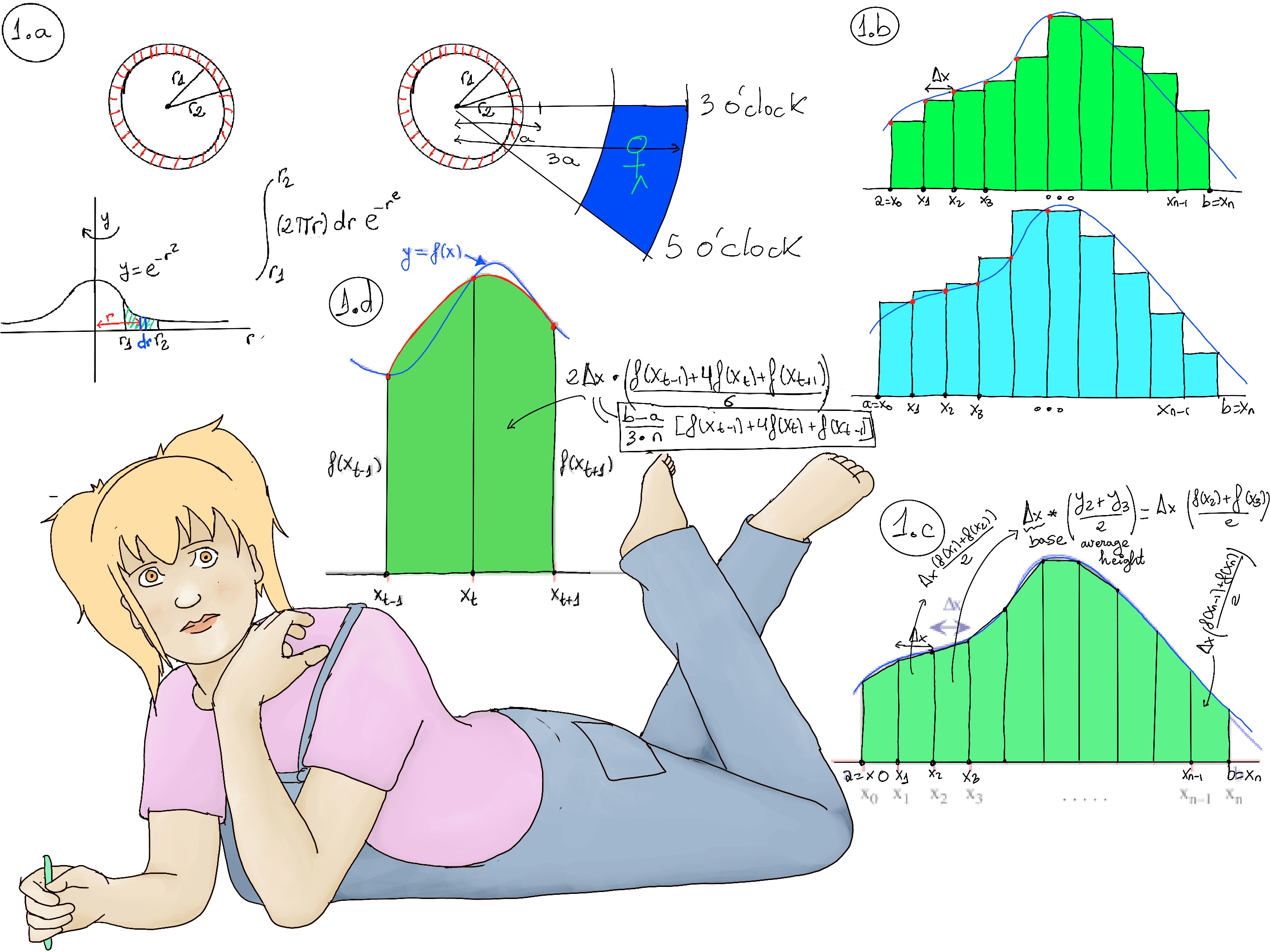
To calculate the probability of a dart landing in the ring, we observe the area between r₁ and r₂ below y = e^-r² and above the r-axis, and compute the volume of revolution of this area revolving about the center of the dart board (y-axis). Taking into consideration that the probability of a hit is constant at any given radio, the probability of hitting inside the ring is $\int_{r_1}^{r_2} (2πr)e^{-r^{2}}dr = -πe^{-r^{2}}\bigg|_{r_1}^{r_2} = -πe^{-r_2^{2}}-(-πe^{-r_1^{2}}) = π(e^{-r_1^{2}}-e^{-r_2^{2}}).$

Recall that the probability function was $ce^{-r^{2}}$, but this fact does not really change our calculations much, so “part” = $cπ(e^{-r_1^{2}}-e^{-r_2^{2}}).$ “whole”, $\int_{0}^{∞} (2πr)e^{-r^{2}}dr = π(e^{0^{2}}-e^{-∞^{2}}) = π(1-0)$. Therefore, whole = cπ ⇒ P(r₁ < r < r₂) = $\frac{cπ(e^{-r_1^{2}}-e^{-r_2^{2}})}{cπ} = e^{-r_1^{2}}-e^{-r_2^{2}}.$

Let’s also assume that the probability of the youngster hitting the target is about 1/2, P(0 ≤ r ≤ a) = 1/2 ↭ P(0 ≤ r ≤ a) = 1/2 ↭ $e^{-0^{2}}-e^{-a^{2}} = \frac{1}{2} ↭ 1 -e^{-a^{2}} = \frac{1}{2} ↭ e^{-a^{2}} = \frac{1}{2}$ 🚀.

To figure out the probability of hitting the little brother, we are going to assume that he’s standing a distance of twice the radio (2a) away from the dart board, and approximate his location by an arc of a ring between 3 o’clock and 5 o’clock to the right of the board, that is 2/12 = 1/6 of a circle.

Therefore, the probability of the little brother getting hit is about ¹⁄₆P(2a ≤ r ≤ 3a) = $\frac{1}{6}(e^{-(2a)^{2}}-e^{-(3a)^{2}})$ =[(2a)² = 4a²] = $\frac{1}{6}((e^{-a^{2}})^{4}-(e^{-a^{2}})^{9})$ = [🚀] = $\frac{1}{6}((\frac{1}{2})^4-(\frac{1}{2})^9) ≈ \frac{1}{6}\frac{1}{16} ≈ \frac{1}{100}$ or 1%.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
10. Chau Tu.