Weighted Average

Pure mathematics is, in its way, the poetry of logical ideas, Albert Einstein.

Recall

Antiderivatives are fundamental concepts in calculus. They are the inverse operation of derivatives.

Given a function f(x), an antiderivative, also known as indefinite integral, F, is the function that can be differentiated to obtain the original function, that is, F’ = f, e.g., 3x² -1 is the antiderivative of x³ -x +7 because $\frac{d}{dx} (x^3-x+7) = 3x^2 -1$. Symbolically, we write F(x) = $\int f(x)dx$.

The process of finding antiderivatives is called integration.

The Fundamental Theorem of Calculus states roughly that the integral of a function f over an interval is equal to the change of any antiderivate F (F'(x) = f(x)) between the ends of the interval, i.e., $\int_{a}^{b} f(x)dx = F(b)-F(a)=F(x) \bigg|_{a}^{b}$

Definition. The average value of a continuous function f(x) over the interval [a, b] is AVG = $\frac{y_1+y_2+···+y_n}{n}$ where y₁, y₂, ···, y_n represent the function values at specific points within the interval [a, b] and n is the total number of points where the function is evaluated within the interval [a, b].

Since integrals are essentially a sum of all of the possible f(x) values, AVG = $\frac{1}{b-a}\int_{a}^{b} f(x)dx$.

Said in a more mathematical way, $\lim_{n \to ∞}\frac{y_1+y_2+···+y_n}{n}$ = $\frac{1}{b-a}\int_{a}^{b} f(x)dx$ where $\int_{a}^{b} f(x)dx$ represents the signed area under the curve of f(x) between x = a and x = b, $\frac{1}{b-a}$ is a scaling factor.

Average Value Theorem. If f is a continuous function on [a, b], then its average or mean value on [a, b] is given by f_avg = $\frac{\int_{a}^{b} f(x)dx}{b-a}$

Weighted Average

A weighted average is a method of computing an average where some elements contribute more than others. In other words, some elements or data points have different weights or importance assigned to them. The weights reflect the relative significance or contribution of each element to the overall average.

The weighted average gives more importance to certain values, elements, or data points in the dataset based on their assigned weights. This type of average is commonly used in various fields and situations where different elements contribute differently to the overall average.

Weighted averages are calculated by multiplying each value by its assigned weight, summing up these products, and then dividing by the sum of all the weights.

The weighted average of a list of elements x₁, ···, x_n with corresponding weights w₁, ···, w_n is $\frac{w_1x_1+w_2x_2 + ··· + w_nx_n}{w_1 + ··· + w_n}$. Note that if the weights are all just 1, that is, all elements or data points have the same importance, then the weighted average is just a plain average.

Exercises

• In finance, a weighted average could be used to calculate the average price of your stock. Let’s suppose that you are interested in investing in a stock, and you bought it for 10, 20, and 25 dollars, and you bought w₁, w₂, and w₃ shares respectively. How much did you spend? 10w₁ + 20w₂ + 25w₃, and the average price is $\frac{10w_1 + 20w_2 + 25w_3}{w_1 + w_2 + w_3}$.

• A general purchases 20,000 units of ammo at 1 each in India, 15,000 at 1.15 each in the USA and 5,000 at 2 each in Germany. We use the price per unit as values and the weight as the total number of units being purchased in every country.

  To calculate the weighted average price per unit of ammo purchased, we need to consider the total cost and the total number of units purchased, that is, you multiply the price per unit by the total number of units for each purchase, sum them up, and then divide by the total number of units purchased = $\frac{1(20,000) + 1.15 (15,000) + 2 (5,000)}{(20,000 + 15,000 + 5,000)} = \frac{(20,000 + 17,250 + 10,000)}{(20,000 + 15,000 + 5,000)} = \frac{47,250}{40,000}$ = 1.18. So, the weighted average price per unit of ammo purchased is $1.18.

• Calculate the average time you spend exercising over a 30-day month. You exercised for 20 minutes on 7 days, 1 hour on 5 days, 45 minutes on 2 weeks, and did not exercise at all for the rest of the month.

To calculate the average time spent exercising over a 30-day month, we need to find the total time spent exercising and then divide it by the total number of days.

Average_Time = $\frac{20·7+60·5+45·14+0·4}{7+5+14+4}≈35.67$, the weighted average time you spent working out for this month was approximately 35.67 minutes per day.

The continuous analogue of a weighted average can be obtained as an integral. Let f be a function defined on an interval [a, b], with weight w(x), a non-negative function on [a, b]. Then, the formula for calculating a weighted average of f on the interval [a, b] is $\frac{\int_{a}^{b} f(x)w(x)dx}{\int_{a}^{b} w(x)dx}$, e.g., f(x) = c ⇒ $\frac{\int_{a}^{b} f(x)w(x)dx}{\int_{a}^{b} w(x)dx} = \frac{c\int_{a}^{b} w(x)dx}{\int_{a}^{b} w(x)dx} = c$.

Solved exercises

• Witches were boiling infants in the cauldron (“in caldari”) until the meat fell off the bones -just kidding. When the witches are boiling water during full moon, the temperature of the water is not the same at each level in the cauldron (y = x² around the y-axis and delimited by y = 5). Obviously, at the bottom of it is at its peak, say 100° C, and at the top 60° C. We are in Halloween, so it is very cold outside, say 0° C, the question is how much heat do they need?

For simplicity sake, let’s define T = 100 -8y. We need to slice the cauldron in disks because at every level, the temperature is indeed constant.

Recall our previous example of the witches’ cauldron with a initial and final temperature with 0° C and 100 -8y respectively. The question is how much energy do we need? We will use the method of disks because the temperature is constant on horizontal levels. Notice that energy equals the product of volume -πx²dy- and temperature -100-8y-, and we are adding up from 0 (bottom) to 5 (top) -Figure 1.c.- .

$\int_{0}^{5} (100-8y)(πx^2)dy = \int_{0}^{5} (100-8y)(πy)dy = \int_{0}^{5} 100πy -8πy^2dy = (50πy^2 -\frac{8}{3}πy^3)\bigg|_{0}^{5} = \frac{2750}{3}π ≈ 47.3333π$ °C·m³.

$\int_{0}^{5} πydy = π\frac{y^2}{2}\bigg|_{0}^{5} = π\frac{25}{2}.$

Therefore, the weighted temperature average equals $\frac{\int_{0}^{5} (100-8y)(πx^2)dy}{\int_{0}^{5} πydy} = \frac{2750}{3}π : π\frac{25}{2} = \frac{5500}{75} ≈ 73.3°$.

• A very similar example is one where witches are boiling water and the temperature of the water is not the same at each level in the cauldron (y = 2·x² around the y-axis and delimited by y = 4). Obviously, at the bottom of it is at its peak, say 90° C, and at the top 50° C. We are in Halloween, so it is very cold outside, say 0° C, T = 90 -10y, the question is what is the weighted temperature average? (Figure 1)

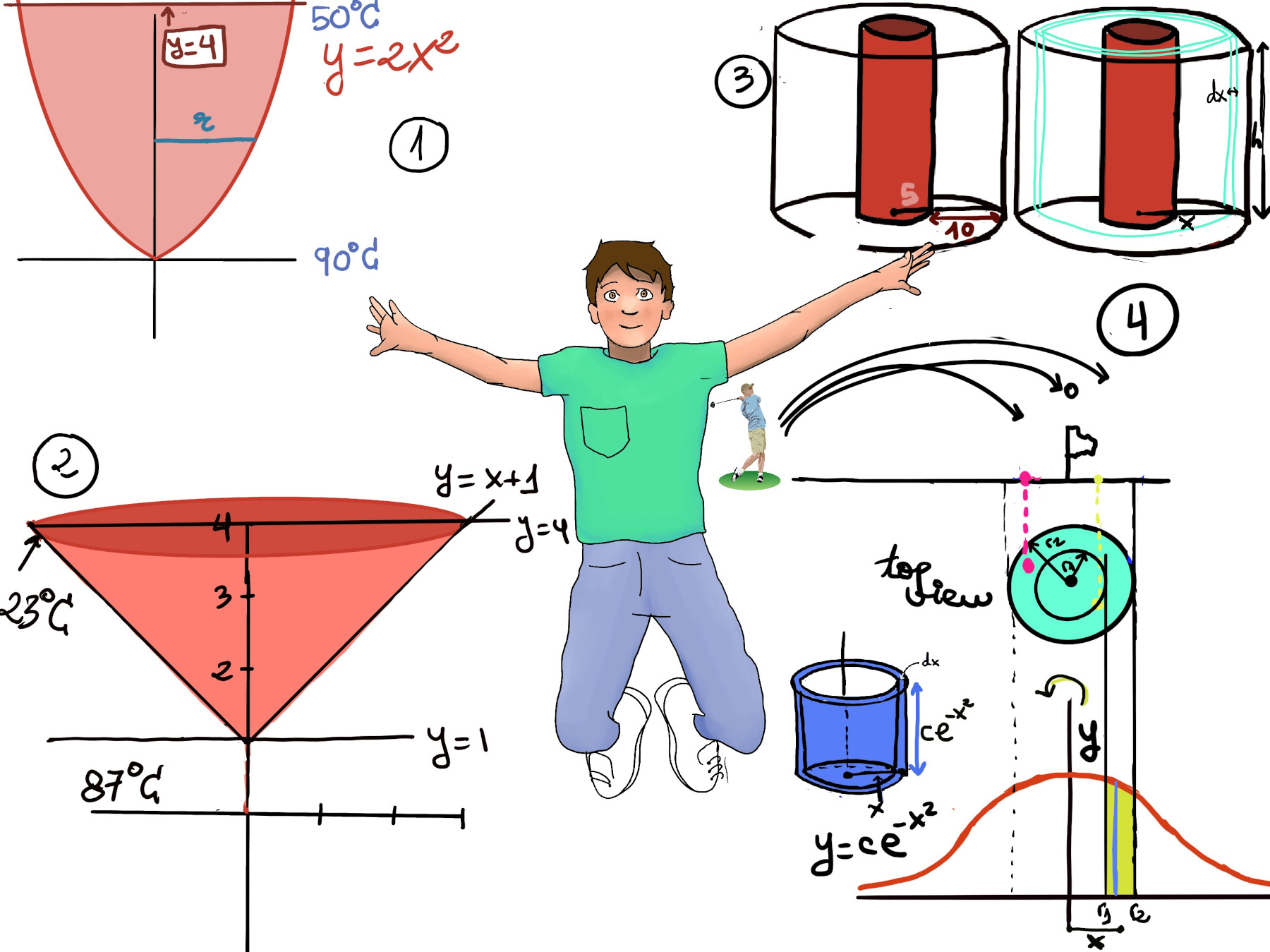
The area of the disks (radius r = x) is πr² =[y = 2x² ⇒ $x = \sqrt{\frac{y}{2}}$]

Therefore, the weighted temperature average equals $\frac{\int_{0}^{4} (90-10y)(π\frac{y}{2})dy}{\int_{0}^{4} π\frac{y}{2}dy} = \frac{\int_{0}^{4} (45y-5y^2)dy}{\int_{0}^{4} \frac{y}{2}dy} = \frac{\frac{45y^2}{2}-\frac{5y^3}{3}}{\frac{y^2}{4}}\bigg|_{0}^{4} = \frac{\frac{45·4^2}{2}-\frac{5·4^3}{3}}{\frac{4^2}{4}} = \frac{360-\frac{320}{3}}{4} = \frac{\frac{760}{3}}{4} = \frac{760}{12} ≈ 63.3°$

• Another variant exercise where the cauldron (solid of revolution) is generated by revolving the line y = x +1 around the y-axis (first quadrant), and delimited by y = 4 and y = 1.The temperature of the water is not the same at each level in the cauldron, it varies from 87°C at the bottom to 23 at y = 4, what is the weighted temperature average? (Figure 2)

The area of the disks (radius r = x) is πr² =[y = x + 1 ⇒ x = y -1]

Let’s suppose that the temperature is uniformly decreasing (in a straight line), and recall that the equation of a line passing through two points is $y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)$ or $y-y_2=\frac{y_2-y_1}{x_2-x_1}(x-x_2)$ ⇒ $T-87=\frac{23-87}{4-1}(y-1) = \frac{-64}{3}(y-1) ↭ 3(T-87) = -64(y-1) ↭ 3T -261 = -64y + 64 ↭ 3T = 325 - 64y$

Average Temperature = $\frac{\int_{1}^{4} (\frac{325 - 64y}{3})π(y-1)^2dy}{\int_{1}^{4} π(y-1)^2dy} = \frac{\int_{1}^{4} (\frac{325 - 64y}{3})(y^2-2y+1)dy}{\int_{1}^{4} (y-1)^2dy} = \frac{\int_{1}^{4} (\frac{325}{3}y^2-\frac{650}{3}y+\frac{325}{3}-\frac{64}{3}y^3+\frac{128}{3}y^2-\frac{64}{3}y)dy}{\int_{1}^{4} (y-1)^2dy} = \frac{\int_{1}^{4} (\frac{-64}{3}y^3+\frac{453}{3}y^2-\frac{714}{3}y+\frac{325}{3})dy}{\int_{1}^{4} (y-1)^2dy} = \frac{\frac{-64}{12}y^4+\frac{453}{9}y^3-\frac{714}{6}y^2+\frac{325}{3}y}{\frac{1}{3}(y-1)^3}\bigg|_{1}^{4} = \frac{385.33-34.33}{9}=39°C$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
10. Chau Tu.