Types of functions.

My appearance had improved substantially, but my pictures could still be sold to scare people, summon the devil, and kill the elderly. I was notice immediately, so many of my coworkers felt embarrassed and avoid hanging with me like eating shit or alien foreskin, Apocalypse, Anawim, #justtothepoint.

Recall

Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).

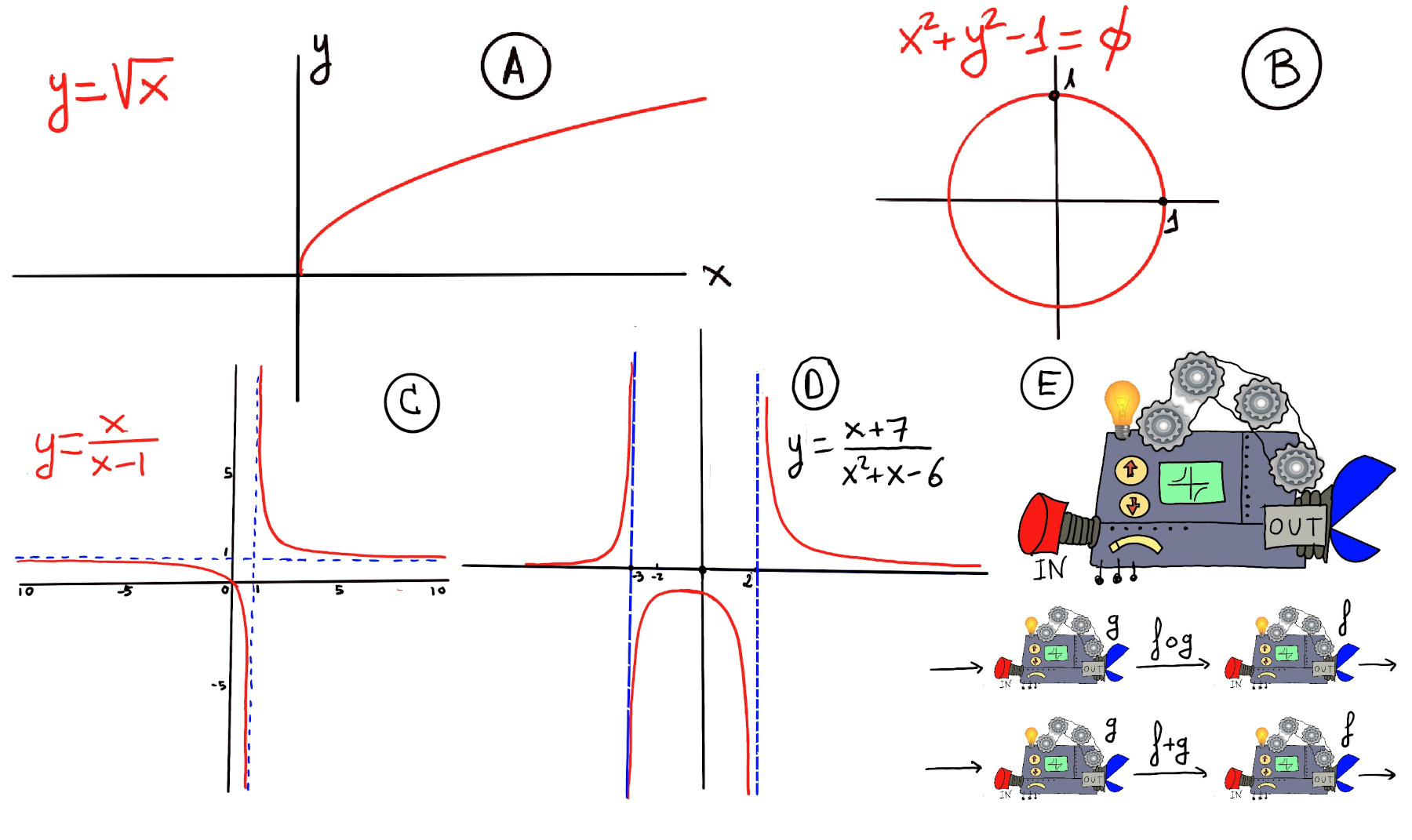
The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ. A mathematical function is like a black box that takes certain input values and generates corresponding output values (Figure E).

Graphing functions involves the visual representation of a curve that reflects the behavior of a mathematical function on a coordinate plane, also known as the Cartesian plane. It is a two-dimensional space defined by two axes - the x-axis (horizontal) and the y-axis (vertical).

A systematic approach to graphing a function begins by constructing a table containing selected input values and their corresponding output values. By extending this table, we can plot the points on the coordinate plane and observe the pattern they form. Connecting these points reveals the shape of the curve, allowing us to gain insights into the behavior of the function across its domain. This process provides a visual means of understanding the relationships between different variables and aids in interpreting the overall characteristics of the function.

Types of functions

There are many types of functions in mathematics. There are different classifications, but some of the common ways to classify functions are based on the following criteria:

• Mapping: one-to-one or injective, many-to-one, onto, and bijective.
• Degree: there are different types of polynomial functions based on the degree of the leading term, such as linear, quadratic, cubic, and so on.
• Symmetry: even (f(x)=f(-x), it has symmetry with respect to the y-axis, e.g., |x|, x²), odd (f(-x)=-f(x), it has rotational symmetry with respect to the origin, that is, its graph remains unchanged after rotation of 180° about the origin, e.g., sgn(x), x, x³), periodic (it has a graph with a basic pattern that repeats at regular intervals, f(x) = f(x + T), e.g., sin(x) is periodic with period 2π).
• Other math concepts: algebraic, transcendental, implicit, parametric, inverse, etc.

Some of the most common types of functions include:

1. Linear functions. f(x) = mx + b, where m and b are constant. The graph is a straight line with a constant slope, m is the slope of the line (it determines the steepness or inclination of the line), e.g., f(x) = 2 (Figure i), f(x) = 3x -1, f(x) = 2x +7, f(x) = ²⁄₃x -2 (Figure ii).

   Algebraic functions are functions that can be expressed as a finite combination of the algebraic operations of addition, subtraction, multiplication, division, and raising to a power. Examples of algebraic functions include polynomial functions (f(x) = a_nxⁿ + a_n-1x^n-1 +···+ a₁x + a₀) and rational functions.

2. Quadratic Functions. A quadratic function is a polynomial with a degree of 2, f(x) =ax² + bx +c, where a, b and c are constants and a ≠ 0. The graph is a parabola with a U-shaped curve. If a > 0, then the parabola opens up “U”. If a < 0, then the parabola opens down “∩”. The vertex is the lowest or highest point on the graph, ($\frac{-b}{2a}, f(\frac{-b}{2a})$), e.g., x²+x -6, its roots are x = -3 and 2, and its vertex is ($\frac{-1}{2}, \frac{-25}{4}$) (Figure iii).

   The roots or zeros of the function are the values of x that make the function equal to zero and you can calculate them by using the quadratic formula, $\frac{-b±\sqrt{b^2-4ac}}{2a}$. Besides, the discriminant, which is the expression b² - 4ac, is used to determine the number and type of roots. If the discriminant is positive, the function has two distinct real roots. If the discriminant is zero, the function has one repeated real root. If the discriminant is negative, the function has two complex roots.

3. Cubic functions. A cubic function is a polynomial with a degree of 3, f(x) =ax³ + bx² +cx +d, where a, b, c and d are constants and a ≠ 0, e.g., f(x) = x³ (Figure iv), f(x) = 4x³ +7x² -5.

4. Exponential functions. An exponential function is a mathematical function of the form f(x) = b·a^x, where the independent variable is the exponent, and a and b are constants. a is called the base of the function and it should be a positive real number (a>0) (Figure v).

   Transcendental functions are functions that are not algebraic, e.g., exponential functions, trigonometric functions, and logarithmic functions.

5. Logarithmic functions. The logarithm is the inverse function to exponentiation. We call the inverse of a^x the logarithmic function with base a, that is, log_ax=y ↔ a^y=x, that means that the logarithm of a number x to the base a is the exponent to which a must be raised to produce x, (Figure v).

6. Trigonometric functions. Trigonometric functions are functions of angles and represent ratios of sides of right triangles. There are six basic trigonometric functions: sine, cosine, tangent, cotangent, secant, and cosecant (Figure vi).

   A periodic function is a function that repeats its values at regular intervals or periods, e.g., the trigonometric functions which repeat at intervals of 2π radians are periodic functions.

    

7. Piecewise functions. We can create functions that behave differently based on the input (x) value. It is a function that defines different expressions for different intervals of the domain.

   $f(x) = \begin{cases} x, &x ≥ 0 \\ -x, &x < 0 \end{cases}$

   This is the absolute value function. The absolute |x| of a real number x is the non-negative value of x without regard to its sign. It is the distance of the number from zero on a number line (Figure viii).

   $f(x) = \begin{cases} -1, &x < 0 \\ 0, &x = 0 \\ 1, &x > 0 \end{cases}$

   This is the sign function. It returns the sign of a real number (Figure vii).

8. Rational functions. It is any function that can be defined by a rational fraction, which is an algebraic fraction (a fraction whose numerator and denominator are algebraic expressions) such that both the numerator and the denominator are polynomials, i.e., f(x) = p(x)/q(x) where p and q are polynomials such that q(x) ≠ 0, e.g., f(x) = $\frac{1}{x^2}$ (it is not defined at x = 0, Figure ix)-, $f(x)=\frac{x^2-5}{x^2+2}$.

9. Step functions. A step or staircase function is a piecewise constant function with a finite number of pieces, that is, it changes its value only at distinct points. Formally, a step function is defined as follows: $f(x) = \begin{cases} c_1 & \text{if } a_1 \leq x < a_2 \\ c_2 & \text{if } a_2 \leq x < a_3 \\ \vdots \\ c_n & \text{if } a_n \leq x < a_{n+1} \end{cases}$

   One of the most commonly used step functions is the greatest integer function. The greatest integer function, also known as the floor function, is a function that returns the largest integer less or equal to the given real number (Figure x). It is denoted by ⌊x⌋ = floor(x) = max{n ∈ ℤ: n ≤ x}, e.g., ⌊2.8⌋ = 2, ⌊4.3⌋ = 4, ⌊-2.3⌋ = -3.

10. Radical functions. Radical functions are mathematical functions that include a radical expression, e.g., the square root function f(x) = $\sqrt{x}$, $\sqrt[3]{x-4}+5$. The square root function is only defined for positive numbers and its curve forms a half-parabola (figure A).  

11. The Dirichlet function is defined as,

    $f(x) = \begin{cases} a, &x ∈ ℚ \\ b, &x ∉ ℚ \end{cases}$ (typically a = 1, b = 0). It is a classic example of a function that is discontinuous everywhere, at every point in its domain.

12. Implicit functions. An implicit function is a function that is defined by an implicit equation. That means the dependent and independent variables are related through an equation, but the dependent variable is not explicitly expressed in terms of the independent variable, e.g., the circle equation x²+y² = r² (figure B), elliptical equation ($\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0$) (a standard ellipse centered at the origin with width 2a and height 2b or semi-major axis a and semi-minor axis b), y² + xy = 0, y² -4x = 0.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.