Derivatives as Rates of Change III

Thinking, wishing, or wanting something does not make it real. Dreams are only dreams and nothing more. Life is not fair nor easy. A lie repeated a thousands times is still a lie. Propaganda and narratives cannot change the facts. Either you deal with what reality is, whether you like it or not, or you can be sure that reality is going to deal with you and chances are that it won’t be nice, JustToThePoint, Anawim, #justtothepoint.

Recall

The derivative of a function at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. It is the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable.

Definition. A function f(x) is differentiable at a point “a” of its domain, if its domain contains an open interval containing “a”, and the limit $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$ exists, f’(a) = L = $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$. More formally, for every positive real number ε, there exists a positive real number δ, such that for every h satisfying 0 < |h| < δ, then |L-$\frac {f(a+h)-f(a)}{h}$|< ε.

1. Power Rule: $\frac{d}{dx}(x^n) = nx^{n-1}$.
2. Sum Rule: $\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))$
3. Product Rule: $\frac{d}{dx}(f(x) \cdot g(x)) = f’(x)g(x) + f(x)g’(x)$.
4. Quotient Rule: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f’(x)g(x) - f(x)g’(x)}{(g(x))^2}$
5. Chain Rule: $\frac{d}{dx}(f(g(x))) = f’(g(x)) \cdot g’(x)$
6. $\frac{d}{dx}(e^x) = e^x, \frac{d}{dx}(\ln(x)) = \frac{1}{x}, \frac{d}{dx}(\sin(x)) = \cos(x), \frac{d}{dx}(\cos(x)) = -\sin(x), \frac{d}{dx}(\tan(x)) = \sec^2(x), \frac{d}{dx}(\arcsin(x)) = \frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arccos(x)) = -\frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arctan(x)) = \frac{1}{1 + x^2}.$

The critical points of a function f are the x-values, within the domain (D) of f for which f’(x) = 0 or where f’ is undefined. Notice that the sign of f’ must stay constant between two consecutive critical points. If the derivative of a function changes sign around a critical point, the function is said to have a local or relative extremum (maximum or minimum) at that point. If f’ changes sign from positive (increasing function) to negative (decreasing function), the function has a local or relative maximum at that critical point. Similarly, if f’ changes sign from negative to positive, the function has a local or relative minimum.

Interpretation

f’(x) is the slope of the line tangent to the graph of f at that particular point (x, f(x)). f’(x) is also the rate of change of the function at x. The average rate of change is the process of calculating the rate at which the output (y-values) changes compared to its input (x-values). This can be visualized as the slope of a secant line passing between two points on a function. In differential calculus, the focus shifts to the instantaneous rate of change, which is found using the derivative of a function.

For example, Growth Rate = $\frac{Births-Deaths}{years}$. The rate of change in population is the derivative of the population function with respect to time, $\frac{dP}{dt}$.

How to solve rates of change problems

You should follow these general steps:

1. Understand the problem, draw a diagram, identify what quantity is changing and with respect to what other quantity.
2. Label all quantities and their rates of change.
3. Relate all quantities in a single equation, that is, use the given information and the problem constraints to set up an equation that relates the quantities involved in the same equation.
4. Differentiate the equation: Calculate the derivative of the equation with respect to the relevant variable to obtain the rate of change.
5. Solve for the unknown: Plug in the known values and solve for the unknown rate of change to answer the question.

Related rates

• A ladder 10 meters long rests against a vertical wall. If the bottom of the ladder slides away from the wall at a rate of 1 m/s, how fast is the top of the ladder sliding down the wall when the bottom of the ladder is 6 meters from the wall.

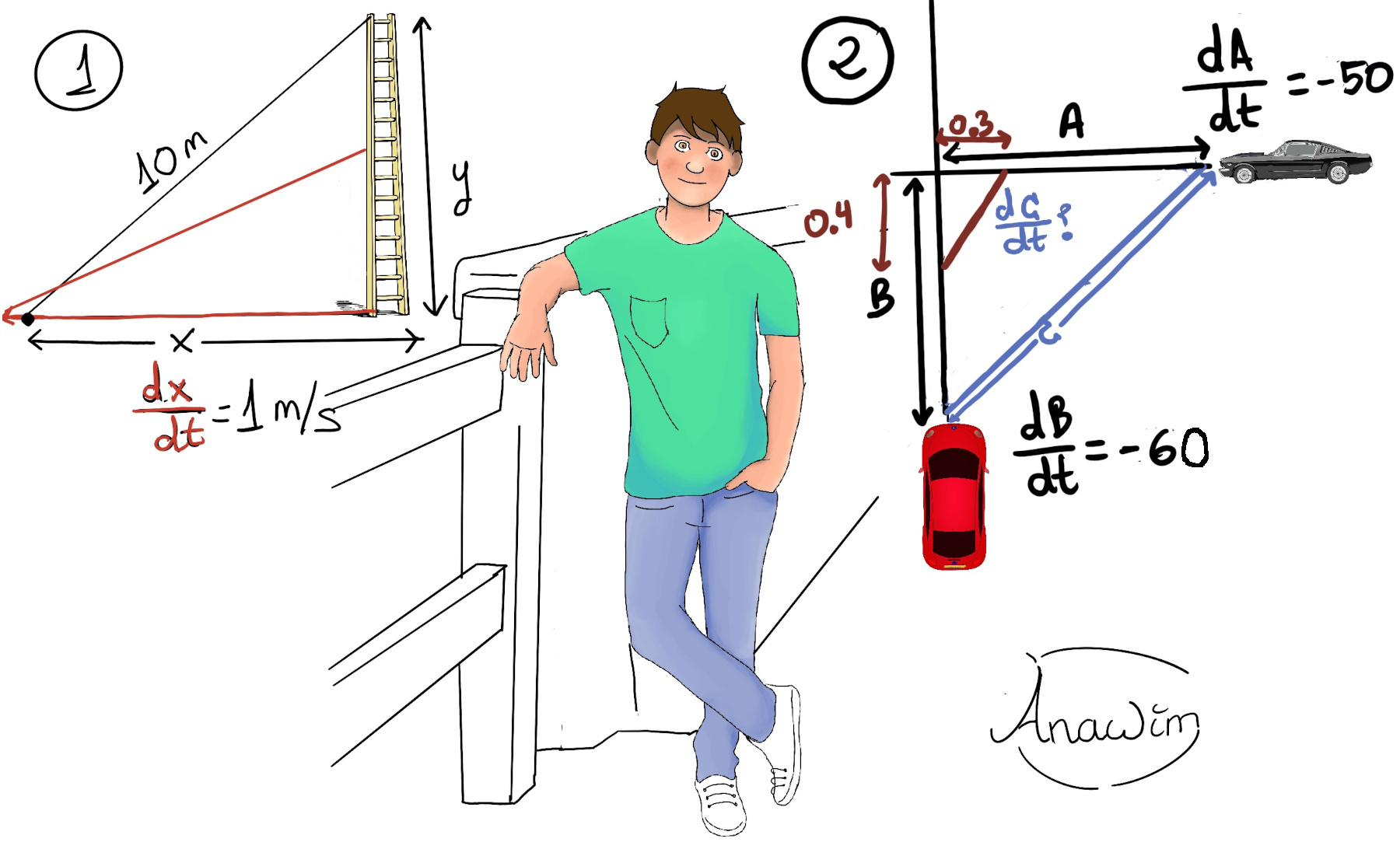
The diagram is shown in Figure 1. By the Pythagorean theorem, x² + y² = 10².

Let’s differentiate by t the previous formula, $2x·\frac{dx}{dt}+2y·\frac{dy}{dt} = 0$ (🚀). Our goal is to calculate $\frac{dy}{dt}$ when x = 6 (⇒ y = $\sqrt{10^2-6^2} = \sqrt{100-36} = \sqrt{64} = 8$), and we also know that $\frac{dx}{dt}=1$, so let’s plug in all of these values in (🚀) $2x·\frac{dx}{dt}+2y·\frac{dy}{dt} = 0 ↭ 2·6·1 + 2·8·\frac{dy}{dt} = 0 ⇒ \frac{dy}{dt} = \frac{-12}{16} = \frac{-3}{4}.$ The top of the ladder is sliding down at a rate of -0.75m/s.

• Car A is travelling west at 50 mph and car B is travelling north at 60 mph. Both are headed for the intersection of the two roads. At what rate are the cars approaching each other when car A is 0.3 meters and car B is 0.4 from the intersection.

The diagram is shown in Figure 2. By the Pythagorean theorem, A² +B² = C². We differentiate by t, $2·A·\frac{dA}{dt}+2·B·\frac{dB}{dt} = 2·C·\frac{dC}{dt}$ [🚀]

We are asked $\frac{dC}{dt}$ when car A is 0.3 meters and car B is 0.4 from the intersection. A = 0.3, B = 0.4 ⇒ $0.3^2+0.4^2 = C^2 ⇒ C = \sqrt{0.25} = 0.5$. We are also told that $\frac{dA}{dt} = -50, \frac{dB}{dt} = -60.$

Let’s plug in all these values in [🚀] ⇒ $2·A·\frac{dA}{dt}+2·B·\frac{dB}{dt} = 2·C·\frac{dC}{dt} ⇒ 2·0.3·(-50) + 2·0.4·(-60) = 2·0.5\frac{dC}{dt} ⇒ \frac{dC}{dt} = -78m/h$, that is, the cars are approaching each other at a rate of 78m/h.

• The volume of a sphere is increasing at a constant rate 12.8·π m³/s. Find the radius of the sphere at the instant when the radius is increasing at a rate of 0.2 m/s.

$\frac{dV}{dt}=12.8·π$. Goal: r when $\frac{dr}{dt} = 0.2$?

Recall that the volume of a sphere is V = $\frac{4}{3}πr^3 ⇒ \frac{dV}{dr} = 4·π·r^2 ⇒ \frac{dr}{dV} = \frac{1}{4·π·r^2}.$

$\frac{dr}{dt} = \frac{dr}{dV}·\frac{dV}{dt} ⇒ 0.2 = \frac{dr}{dV}·\frac{dV}{dt} = \frac{1}{4·π·r^2}·12.8 ⇒ r^2 = \frac{12.8·π}{0.2·4·π} = \frac{12.8}{0.8} = 16 ⇒ r = ±4$ ⇒[A radius is obviously positive] r = 4m.

• A police car, approaching a right-angled intersection from the north, is chasing a fast sports car that has turned the corner and is now moving straight east. When the police car is 0.6 miles north of the intersection and the car is 0.8 miles to the east, the police determine with a radar gun that the distance between them and the car is increasing at 20 mph. If the police car is moving at 60 mph at the instant of measurement, what is the speed of the car?

The diagram is shown in Figure E. By the Pythagorean theorem, x² + y² = z² ⇒[We differentiate by t] $2x\frac{dx}{dt} +2y\frac{dy}{dt}= 2z\frac{dz}{dt}$

Our goal is $\frac{dx}{dt}$ when y = 0.6, x = 0.8 (x² + y² = z² ↭ $z = \sqrt{0.6^2+0.8^2}$ = 1), $\frac{dz}{dt} = 20, \frac{dy}{dt} = -60$.

Let’s plug in these values into the previous formula, $2x\frac{dx}{dt} +2y\frac{dy}{dt}= 2z\frac{dz}{dt} ⇒ 2·0.8·\frac{dx}{dt} +2·0.6·(-60) = 2·1·20 ⇒ 1.6·\frac{dx}{dt} = 40+72 ⇒ \frac{dx}{dt} = \frac{40+72}{1.6} = 70mph.$

• You are observing a rocket launch from an observation post 5,000 meters from the launch pad. When it reaches an altitude of 10,000 meters, it is traveling at a rate of 200 meters per second. How fast is the rocket moving away from you at this moment? (Figure D)

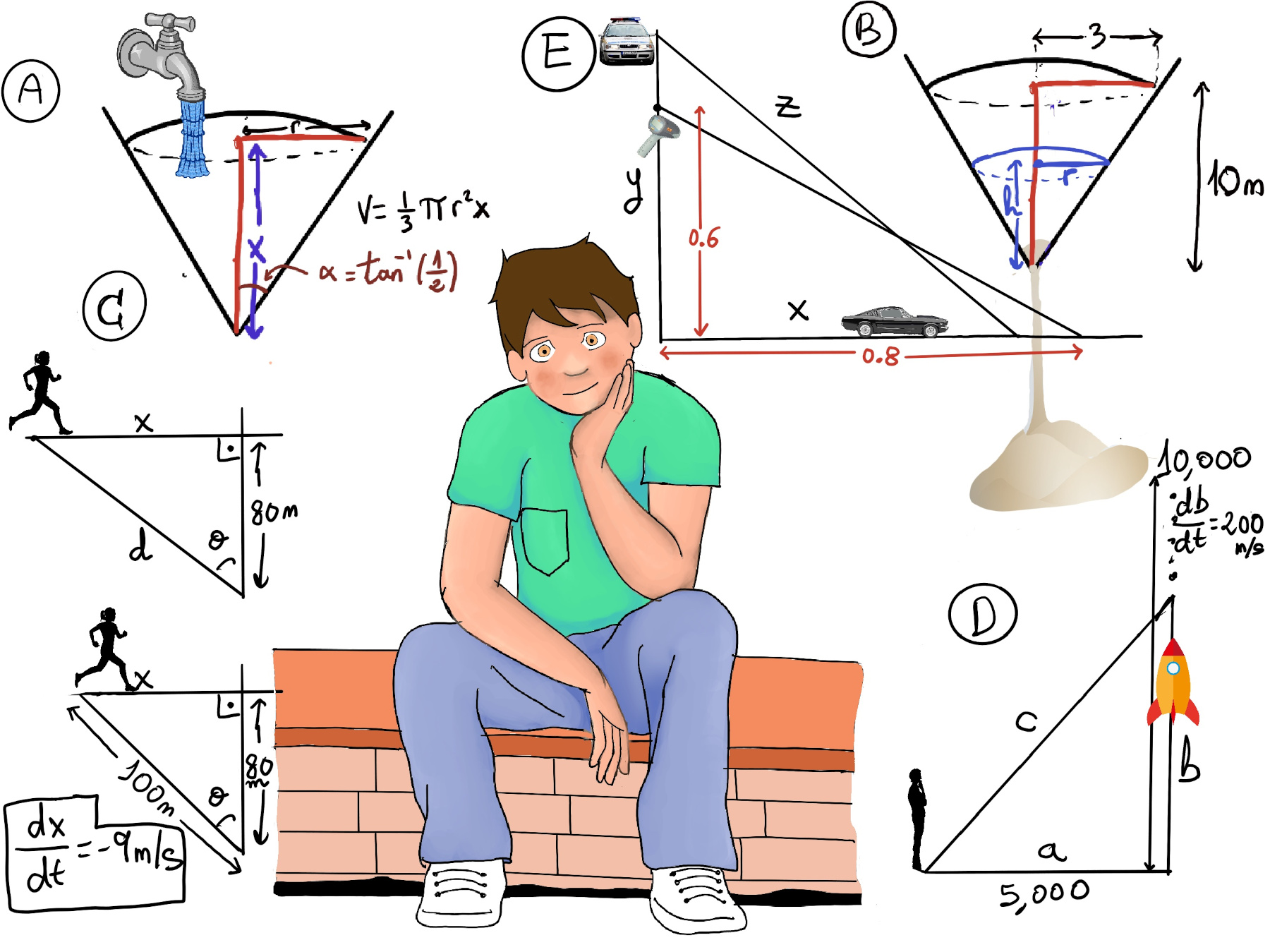
a = 5,000 meters. $\frac{db}{dt}\bigg|_{10,000} = 200m/s$

a² + b² = c². In that particular moment, $5,000^2+10,000^2 = c^2⇒ c = \sqrt{5,000^2+10,000^2} = \sqrt{5,000^2+5,000^2·2^2} = 5,000\sqrt{1+2^2} = 5,000·\sqrt{5}$

a² + b² = c² ⇒ $\frac{d(a^2+b^2)}{dt} = \frac{dc^2}{dt} ⇒ 2a·\frac{da}{dt}+2b·\frac{db}{dt} = 2c\frac{dc}{dt} ⇒ 2·5,000·0+2·10,000·200 = 2·5,000·\sqrt{5}·\frac{dc}{dt} ⇒ 4,000,000 = 10,000\sqrt{5}·\frac{dc}{dt} ⇒ \frac{dc}{dt}=\frac{4,000,000}{10,000·\sqrt{5}} = \frac{400}{\sqrt{5}}=\frac{400·\sqrt{5}}{\sqrt{5}·\sqrt{5}} = \frac{400·\sqrt{5}}{5} = 80·\sqrt{5}m/s.$

• The volume of water in a reservoir is given by V = $3·(2 + \sqrt{h})^6-192$ where V is volume in cubic metres and h is the dept of water in meters. Water is flowing into the reservoir at a constant rate of 150 cubic meters per hours. Find the rate at which the depths of water is increasing at the instant where the depths is 1.4m.

$\frac{dV}{dt}=150, \frac{dh}{dt}\bigg|_{h=1.4}?$

V = $3·(2 + \sqrt{h})^6-192 ⇒ \frac{dV}{dt} = 150 = 3·6·(2 + \sqrt{h})^5\frac{1}{2\sqrt{h}}\frac{dh}{dt}⇒\frac{dh}{dt} = \frac{150·\sqrt{h}}{9·(2 + \sqrt{h})^5}$

$\frac{dh}{dt}\bigg|_{h=1.4} = \frac{150·\sqrt{1.4}}{9·(2 + \sqrt{1.4})^5}$ ≈ 0.06 m/s.

• An airplane is flying horizontally at 480mph, 3miles above the ground when it passes a boy on the ground. How fast is the distance between the boy and the plane increasing half a minute later?

We know that 3² + b² = c², $\frac{db}{dt}=480$

480 miles ———- 1h = 60*60 seconds
b miles ———— 30 seconds

b = $\frac{480·30}{60·60} = 4 miles$ ⇒[3² + b² = c²] c = 5.

The diagram is shown in Figure 2.b.  

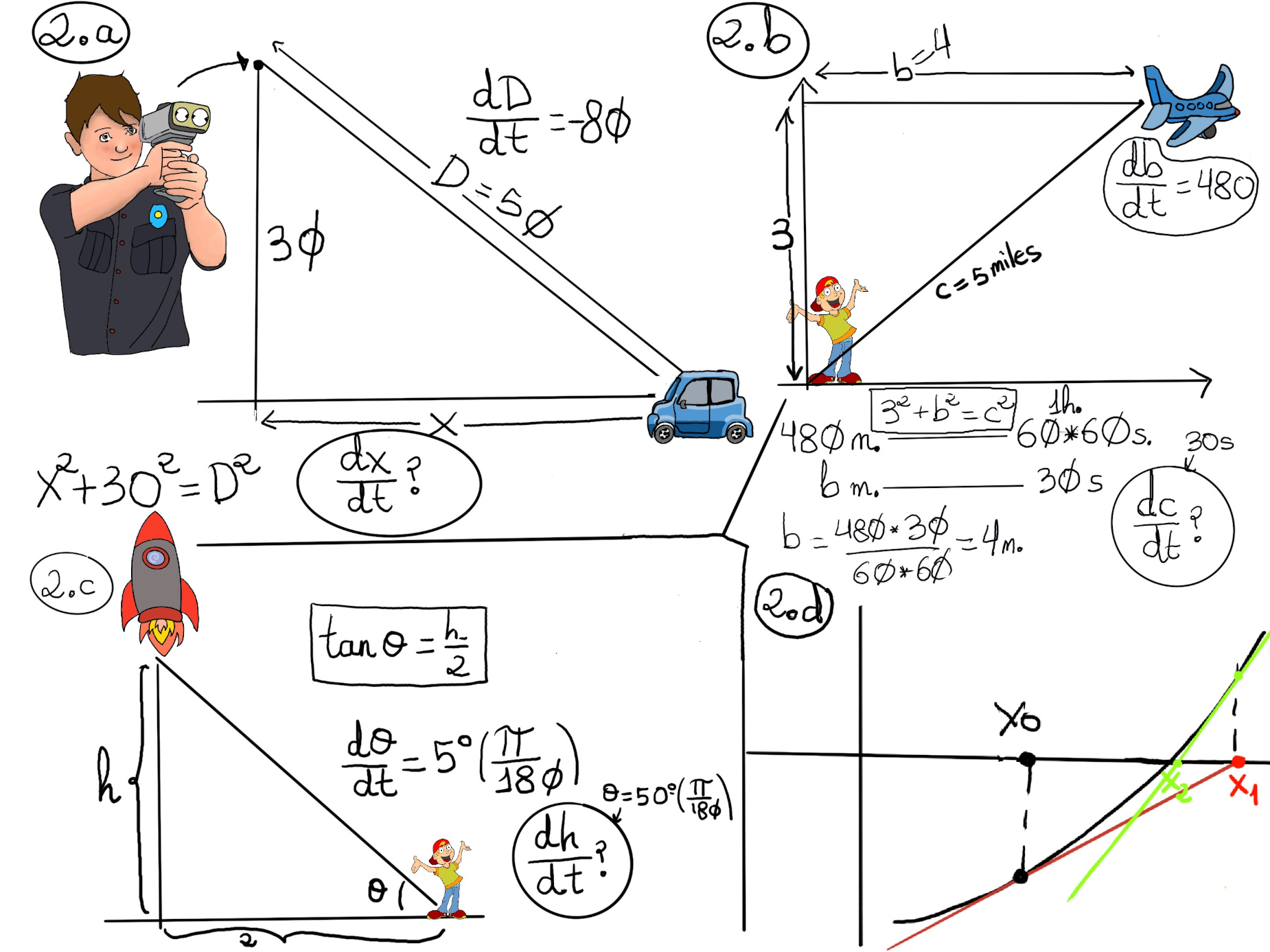
3² + b² = c² ⇒ 2b$\frac{db}{dt} = 2c\frac{dc}{dt}$. Now, we can insert the values in this equation, $2·4·480 = 2·5·\frac{dc}{dt}⇒~ \frac{dc}{dt}=384mph$∎

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.