No pressure, no diamonds, Thomas Carlyle.
Recall
The derivative of a function at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. It is the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable.
Definition. A function f(x) is differentiable at a point “a” of its domain, if its domain contains an open interval containing “a”, and the limit $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$ exists, f’(a) = L = $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$. More formally, for every positive real number ε, there exists a positive real number δ, such that for every h satisfying 0 < |h| < δ, then |L-$\frac {f(a+h)-f(a)}{h}$|< ε.

- Power Rule: $\frac{d}{dx}(x^n) = nx^{n-1}$.
- Sum Rule: $\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))$
- Product Rule: $\frac{d}{dx}(f(x) \cdot g(x)) = f’(x)g(x) + f(x)g’(x)$.
- Quotient Rule: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f’(x)g(x) - f(x)g’(x)}{(g(x))^2}$
- Chain Rule: $\frac{d}{dx}(f(g(x))) = f’(g(x)) \cdot g’(x)$
- $\frac{d}{dx}(e^x) = e^x, \frac{d}{dx}(\ln(x)) = \frac{1}{x}, \frac{d}{dx}(\sin(x)) = \cos(x), \frac{d}{dx}(\cos(x)) = -\sin(x), \frac{d}{dx}(\tan(x)) = \sec^2(x), \frac{d}{dx}(\arcsin(x)) = \frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arccos(x)) = -\frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arctan(x)) = \frac{1}{1 + x^2}.$
The critical points of a function f are the x-values, within the domain (D) of f for which f’(x) = 0 or where f’ is undefined. Notice that the sign of f’ must stay constant between two consecutive critical points. If the derivative of a function changes sign around a critical point, the function is said to have a local or relative extremum (maximum or minimum) at that point. If f’ changes sign from positive (increasing function) to negative (decreasing function), the function has a local or relative maximum at that critical point. Similarly, if f’ changes sign from negative to positive, the function has a local or relative minimum.
Interpretation
f’(x) is the slope of the line tangent to the graph of f at that particular point (x, f(x)). f’(x) is also the rate of change of the function at x. The average rate of change is the process of calculating the rate at which the output (y-values) changes compared to its input (x-values). This can be visualized as the slope of a secant line passing between two points on a function. In differential calculus, the focus shifts to the instantaneous rate of change, which is found using the derivative of a function.
For example, Growth Rate = $\frac{Births-Deaths}{years}$. The rate of change in population is the derivative of the population function with respect to time, $\frac{dP}{dt}$.
How to solve rates of change problems
You should follow these general steps:
- Understand the problem, draw a diagram, identify what quantity is changing and with respect to what other quantity.
- Label all quantities and their rates of change.
- Relate all quantities in a single equation, that is, use the given information and the problem constraints to set up an equation that relates the quantities involved in the same equation.
- Differentiate the equation: Calculate the derivative of the equation with respect to the relevant variable to obtain the rate of change.
- Solve for the unknown: Plug in the known values and solve for the unknown rate of change to answer the question.
- Suppose we drop a brick from the top of a 100 meters building and time its fall. (Credits: David Lippman from Shana Calaway’s remix of Contemporary Calculus by Dale Hoffman. It is licensed under the Creative Commons Attribution license, Figure i)
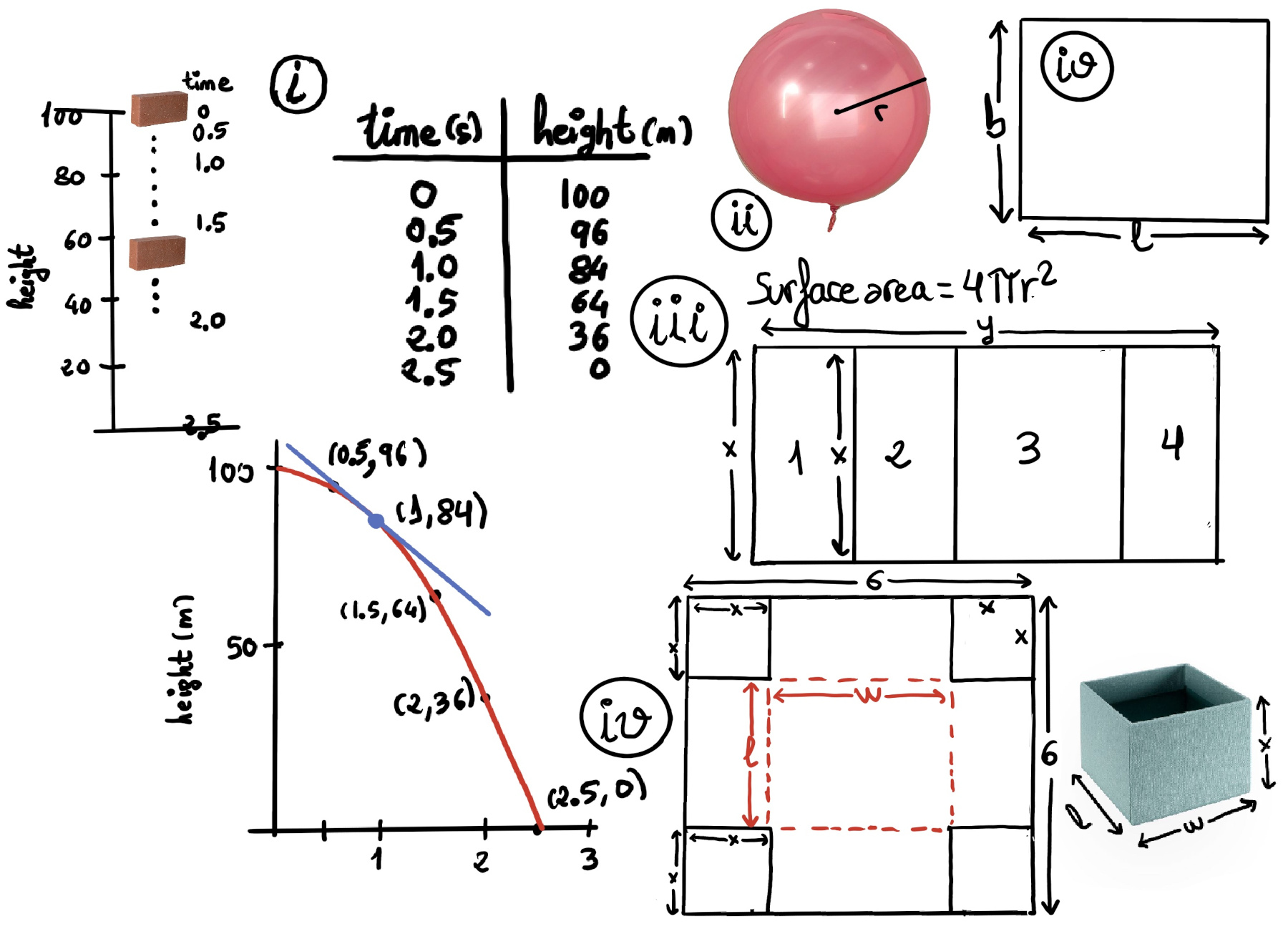
Some questions are relatively easy to answer directly from the table:
- How long did it take for the brick to drop 100 metres? 2.5 seconds.
- How far did the brick fall during the first second and the first two seconds? 100 -84 = 16 m. and 100 – 36 = 64 m. respectively.
- How far did the brick fall during the last second and a half? 84 – 0 = 84 meters.
- How far did the brick fall between t = 0.5 and t=1.5? 96 – 64 = 32 meters.
- What was the average velocity of the brick during its fall? Average_velocity = $\frac{distance fallen}{total time} = \frac{-100 meters}{2.5 seconds} = -40m/s.$
- What was the average velocity between t=1 and t=2 seconds? Average_velocity = $\frac{Δ position}{Δ time} = \frac{36m-84m}{2s-1s} = -48m/s.$
- How fast was the brick falling 1 second after it was dropped? The question is asking for the instantaneous velocity.
The worst approximation after 1 second is simply the average velocity during the entire fall, namely, -40m/s. This is not a good one, because the brick fell very slowly at the begging and started accelerating later on.
A better approximation is the average velocity between t = 0.5 and t = 1 ($=\frac{84-96m}{0.5s}=\frac{-12m}{0.5s}=-24m/s$) or between t = 1 and t = 1.5 ($=\frac{64-84m}{0.5s}=\frac{-20m}{0.5s}=-40m/s$) ⇒ The instantaneous velocity is between -24m/s and -40m/s, but the mathematical solution is the slope of the tangent line to the graph at t = 1, $\lim_{\Delta time \to 0} \frac{Δ position}{Δ time}$. However, we cannot calculate it because the algebraic form of the function is not known.
- The temperature, T, in degrees Celsius, of a cold yam placed in a hot oven is given by T = f (t), where t is the time in minutes since the yam was put in the oven.
- What is the sign of f’(t)? Why? The sign of f’(t) is probably positive since the temperature of the yam is an increasing function, that is, the slopes of tangents of f are positive.
- What are the units of f’(20)? What is the practical meaning of the statement f’(20)=2? f’(20) = $\frac{dT}{dt}\bigg|_{t=20} = 2°C/min,$ meaning that 20 minutes after the yam was put in the oven, the temperature of the yam was increasing at a rate of 2°C/min.
- Approximate f(22) if f(20) = 150. As 22 is relatively close to 20, f(22) ≈ f(20)+f’(20)(22 -20) = 150 + 2·2 = 154°C.
- The radius of a circle is increasing at a rate of 3m per second. Find the rate of change of the circle’s area when r = 10m.
$\frac{dr}{dt} = 3$, Goal: $\frac{dA}{dt}\bigg|_{r=10}$
The area of a circle is π times the radius squared. A = πr2 ⇒ $\frac{dA}{dt} = 2πr\frac{dr}{dt} = 2πr·3 = 6πr$, hence $\frac{dA}{dt}\bigg|_{r=10} = 6π·10 = 60π$m2/s.
- The length of a cube is increasing at a rate of 5m per second. Find the rate of change of the cube’s volume when the length is 20m.
$\frac{dl}{dt}=5m$, Goal: $\frac{dV}{dt}\bigg|_{l=20}$
The volume of a cube is equal to the length of a side cubed, V = l3 ⇒ $\frac{dV}{dt} = 3·l^2·\frac{dl}{dt} = 3·l^2·5=15·l^2.$
Goal: $\frac{dV}{dt}\bigg|_{l=20} = 15·(20)^2 = 6000m^3.$
- A car and a lorry are approaching an intersection on roads that are perpendicular to each other. The car is 0.8 miles and traveling at 60mph. The lorry is 0.6 miles from the intersection and traveling at 30mph. Find the rate of change of the distance between the two cars.
Goal: $\frac{ds}{dt}$?
$\frac{dy}{dt}=-60mph, \frac{dx}{dt}=-30mph $.
The diagram is shown in Figure 1.e.
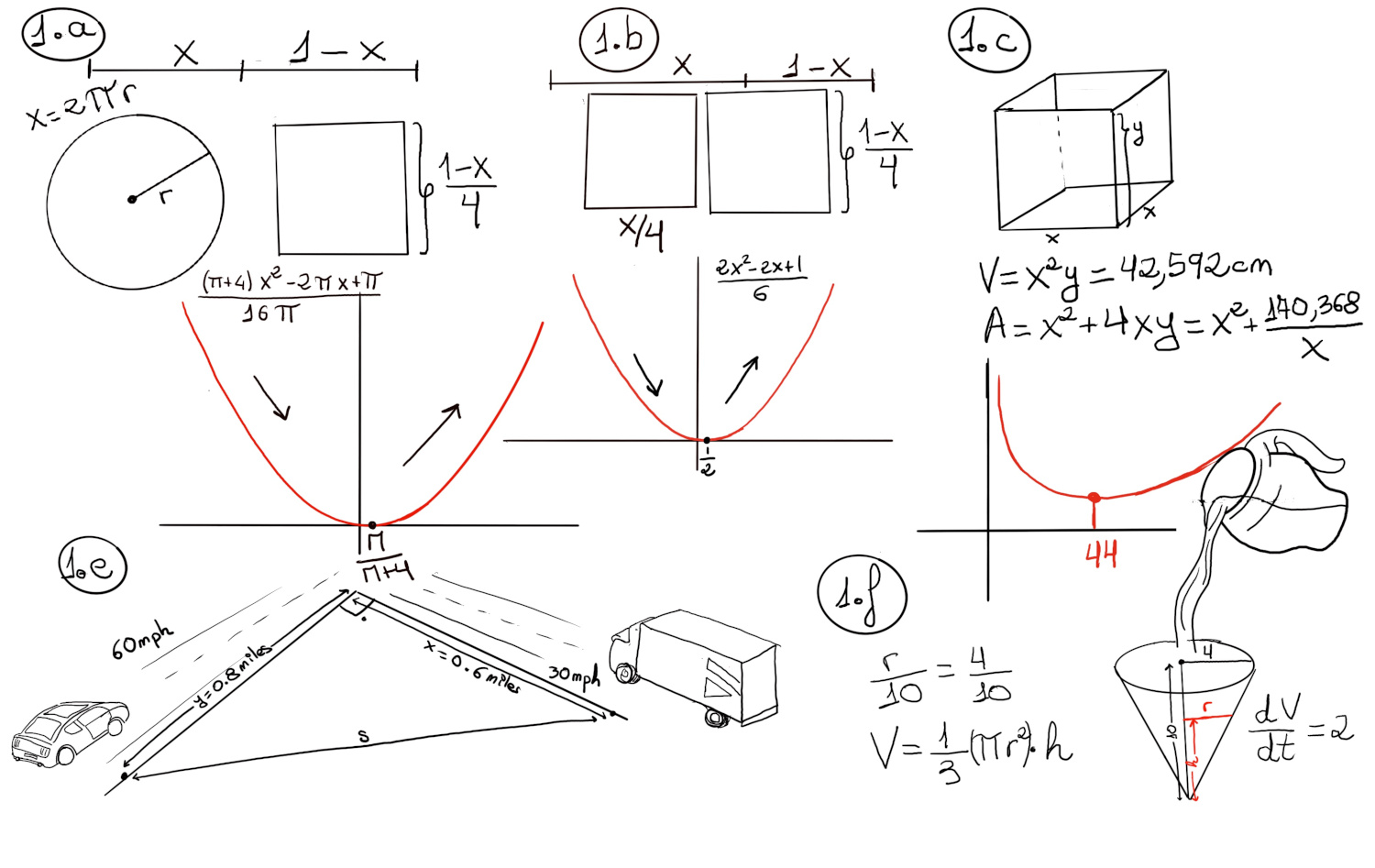
By the Pythagorean theorem (we can never thank him enough 😃), $x^{2} + y^{2}=s^{2} ⇒ 0.6^{2} + 0.8^{2}=s^{2} ⇒ s= \sqrt{0.6^{2} + 0.8^{2}} = 1$
$x^{2} + y^{2}=s^{2} ⇒ 2x\frac{dx}{dt}+2y\frac{dy}{dt}=2s\frac{ds}{dt} ⇒ 2·0.6·(-30)+2·0.8·(-60)=2·1·\frac{ds}{dt} ⇒ \frac{ds}{dt}=-66mph.$
- A balloon is being inflated in a theme park by a funny clown (this detail is extremely important as it won’t be later on discussed). The radius of the ballon is increasing at a rate of 12 m per hour. Find the rate at which the surface area of the balloon is increased at the instant when the radius is 150m (Figure 2).
Recall: The surface area of a sphere is given by the formula: A=4πr2 where A is the surface area and r is the radius of the sphere.
Constraints: $\frac{dr}{dt} = 12$
A=4πr2 ⇒ $\frac{dA}{dt} = 4π(2r)\frac{dr}{dt} = 4π(2·r)12$, so the rate at which the surface area is increased when the radius is 150m equals $\frac{dA}{dt}\bigg|_{r=150} = 4π(2·150)12 = 45200m^2$.
- Consider a conical tank. Its radius at the top is 4 feet, and its 10 feet high. Its being filled with water at the rate of 2 cubic feet per minute. How fast is the water level rising when it is 5 feet high?
The radius and height of the inverted cone as it is being filled are r and h respectively. Two triangles are similar when they have equal angles and proportional sides, and therefore $\frac{r}{h} = \frac{4}{10}$ ⇒ r = $\frac{2h}{5}$.
The diagram is shown in Figure 1.f.

$V = \frac{1}{3}·base·height=\frac{1}{3}·\pi·r^{2}·h =$[ r = $\frac{2h}{5}$] $\frac{4\pi}{75}·h^{3}$
By our problems’s formulation, we assume that $\frac{dV}{dt}=2$ cubic feet per minute.
Goal: h = 5, $\frac{dh}{dt}|_{h=5}?$
$\frac{dV}{dt}=2=\frac{4\pi}{75}·3h^{2}·\frac{dh}{dt} = \frac{4\pi}{25}·h^{2}·\frac{dh}{dt}$ ⇒ $2 = \frac{4\pi}{25}·5^{2}·\frac{dh}{dt} = 4\pi·\frac{dh}{dt} ⇒ \frac{dh}{dt}|_{h=5} = \frac{2}{4\pi} = \frac{1}{2\pi}$ft/sec.
Bibliography
This content is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
- NPTEL-NOC IITM, Introduction to Galois Theory.
- Algebra, Second Edition, by Michael Artin.
- LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
- Field and Galois Theory, by Patrick Morandi. Springer.
- Michael Penn, and MathMajor.
- Contemporary Abstract Algebra, Joseph, A. Gallian.
- YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
- MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
- Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.









