Optimization Problems II

For every problem there is always, at least, a solution which seems quite plausible and reasonable. It is simple and clean, direct, neat, and very nice, and yet it is plainly wrong, #Anawim, justtothepoint.com

Recall

The derivative of a function at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. It is the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable.

Definition. A function f(x) is differentiable at a point “a” of its domain, if its domain contains an open interval containing “a”, and the limit $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$ exists, f’(a) = L = $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$. More formally, for every positive real number ε, there exists a positive real number δ, such that for every h satisfying 0 < |h| < δ, then |L-$\frac {f(a+h)-f(a)}{h}$|< ε.

1. Power Rule: $\frac{d}{dx}(x^n) = nx^{n-1}$.
2. Sum Rule: $\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))$
3. Product Rule: $\frac{d}{dx}(f(x) \cdot g(x)) = f’(x)g(x) + f(x)g’(x)$.
4. Quotient Rule: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f’(x)g(x) - f(x)g’(x)}{(g(x))^2}$
5. Chain Rule: $\frac{d}{dx}(f(g(x))) = f’(g(x)) \cdot g’(x)$
6. $\frac{d}{dx}(e^x) = e^x, \frac{d}{dx}(\ln(x)) = \frac{1}{x}, \frac{d}{dx}(\sin(x)) = \cos(x), \frac{d}{dx}(\cos(x)) = -\sin(x), \frac{d}{dx}(\tan(x)) = \sec^2(x), \frac{d}{dx}(\arcsin(x)) = \frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arccos(x)) = -\frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arctan(x)) = \frac{1}{1 + x^2}.$

The critical points of a function f are the x-values, within the domain (D) of f for which f’(x) = 0 or where f’ is undefined. Notice that the sign of f’ must stay constant between two consecutive critical points. If the derivative of a function changes sign around a critical point, the function is said to have a local or relative extremum (maximum or minimum) at that point. If f’ changes sign from positive (increasing function) to negative (decreasing function), the function has a local or relative maximum at that critical point. Similarly, if f’ changes sign from negative to positive, the function has a local or relative minimum.

Steps to solve an optimization problem.

1. Understand the Problem. The first step is to thoroughly read the problem statement multiple times to ensure a clear understanding, including the quantity that needs to be optimized (maximized or minimized) and any constraints that must be satisfied.
2. Represent the problem, make a diagram.
3. Find the Objective Function. Express the quantity to be optimized as a function of one or more variables. This function could represent a cost, profit, area, volume, or any other relevant quantity. Using the problem constraints, one variable could be expressed in terms of the others, resulting in a function of a single variable that can be optimized.
4. Find critical points. This step involves calculating the derivative of the function with respect to the variable that has been expressed in terms of the others and setting the derivative equal to zero to find the function’s critical points.
5. Determine whether critical points correspond to local maxima, local minima, or saddle points of the graph by using the first and second derivative tests.
6. Interpret the results in the context of the problem to determine the optimal solution and check that the optimal solution being found makes sense.

Optimization problems II

• A rectangular garden is to be constructed using a rock wall as one side of the garden and wire fencing for the other three sides. Given that there are 100 meters of fencing available, determine the dimensions that would create the garden of maximum area. You may enter an exact answer or round it to the nearest hundredth.

Understand/Represent the problem, (Figure 4).

Let x and y denote the width and length of the rectangular garden, that is, y is the side of the rectangle to be constructed with a rock wall.

Find the Objective Function. Area of the rectangular garden, A = x · y. Perimeter of the rectangular area = 2·x + 2·y, but in this particular case only one side y will be fenced with wire ⇒[Constraint: there are 100 meters of fencing available] 2x + y = 100 ⇒ y = 100 -2x ⇒ A = x · y = x·(100-2x) = 100x -2x².

Find critical points: $\frac{dA}{dx} = 100 -4x = 0 ⇒ x = \frac{-100}{-4} = 25.$

Determine whether critical points correspond to local maxima, local minima, or saddle points.

Recall Second Derivative Test. Let f be a function defined on a closed interval I that is twice differentiable at a point “a” (Obviously, a ∈ I).

1. f has a local maximum at a if f’(a) = 0, and f’’(a) < 0.
2. f has a local minimum at a if f’(a) = 0, and f’’(a) > 0.
3. The test fails if f’(a) = f’’(a) = 0.

$\frac{d^2A}{dx^2} = -4 < 0$ ⇒ A has a local maximum at x = 25.

Interpret the results. To optimize (maximize) the area of the garden, let x = 25m and y = 100 -2·25 = 50m, and the area of the garden would be 25·50 = 1250m².

• A box with a square base and open top must have a volume of 42,592m³. Find the dimensions of the box that minimize the amount of material used.

Understand/Represent the problem, the diagram is shown in Figure 1.c.

V = x²y = 42,592 ⇒ y = $\frac{V}{x^{2}} = \frac{42,592}{x^{2}}$

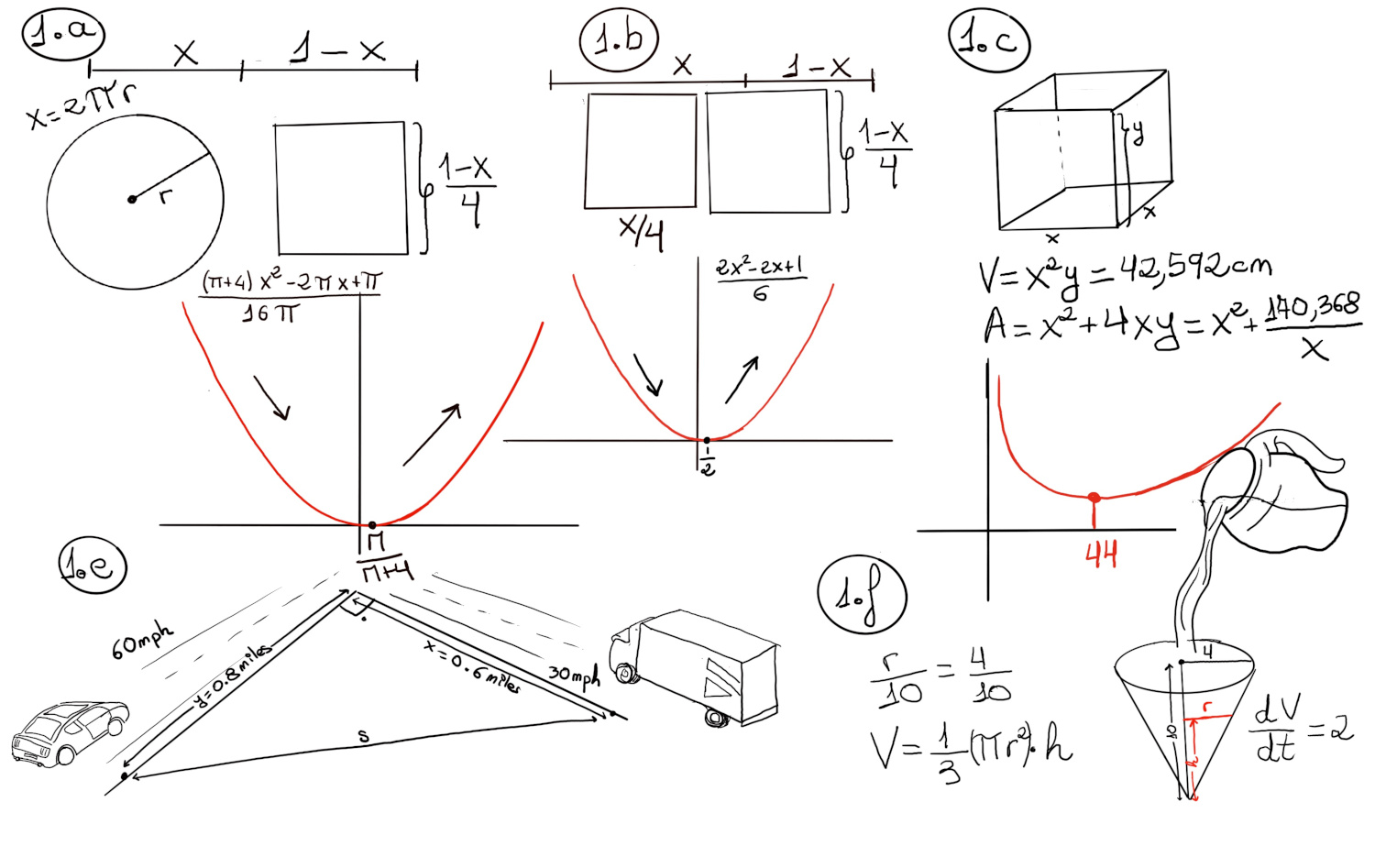
Find the Objective Function. A = x² (base) +4xy (4 sides) + 0 (no top) = $ x^2+4·x·\frac{42,592}{x^{2}} = x^2+\frac{170,368}{x}$

Find critical points: $\frac{dA}{dx} = 2x -\frac{170,368}{x^2}, \frac{dA}{dx} = 0 ⇒ 2x -\frac{170,368}{x^2} = 0 ⇒ 0 = \frac{2x^{3}-170,368}{x^{2}}$ ⇒ $x = \sqrt[3]{\frac{170,368}{2}}≈44$

Determine whether critical points correspond to local maxima, local minima, or saddle points.

1. (0, 44), $\frac{dA}{dx}$ < 0 ⇒ A is decreasing.
2. (44, ∞), A’>0 ⇒ A is increasing ⇒ x= 44 is a minimum.

   Alternative method. $\frac{dA^2}{dx}$ = 2 + ^2*170,368⁄_x³ >0 ⇒ Concave upward ⇒ 44 is a minimum.

Interpret the results. y = $\frac{V}{x^{2}} = \frac{42,592}{x^{2}} = \frac{42,592}{44^{2}}$ ≈ 22 ⇒ Dimensions: 44m x 44 m x 22 m. A = x² (base) +4xy (4 sides) + 0 (no top) = 44² +4·44·22 = 5,808 m³.

• What is the maximum volume you can get for an open box constructed by removing squares of size x from each corner of a paper that is 6 m by 6 m and folding up the sides?

Understand/Represent the problem, (Figure iv)

Length and breadth of the open box are l = w = (6–2x) m and height = x m.

Find the Objective Function, V(x) = (6 -2x)·(6 -2x)·x m³ = (36 -24x +4x²)·x = 36x -24x² +4x³.

Find critical points: $\frac{dV}{dx} = 36 -48x +12x^2= 0 ↭ x^2-4x + 3 = 0 ⇒ x = \frac{4±\sqrt{4^2-4·3·1}}{2·1} = \frac{4±\sqrt{4}}{2} = \frac{4±2}{2} = $ 3m (this is not possible) or 1m.

Determine whether critical points correspond to local maxima, local minima, or saddle points.

$\frac{d^2V}{dx^2} = -48 +24x$ at x = 1, $\frac{d^2V}{dx^2}\bigg|_{1} =$ -48 + 24 = -24 < 0 ⇒ there exists a maximum.

Interpret the results. To maximize the volume, put x = 1 meter, and the volume would be V(1) = (6 -2·1)·(6 -2·1)·1 = 4·4·1 = 16 m³.

• A rectangular flower garden with an area of 30 m² is surrounded by a fenced border 1 m wide on two sides and 2 m wide on the other two sides. What dimensions of the garden minimize the combined area of the garden and borders?

Understand/Represent the problem, Figure 3.

Our area’s flower garden = 30 = x·y (i). The combined area of the garden and border A = (x + 4)·(y + 2) (ii).

Find the Objective Function. 30 = x·y (i) ⇒ y = $\frac{30}{x}$ ⇒[Replacing y into (ii)] A = $(x + 4)·(\frac{30}{x}+2)= (x +4)(\frac{30+2x}{x}) = (\frac{(x+4)(30+2x)}{x}) = \frac{2x^2+38x120}{x} = 2x + 38 + \frac{120}{x}$

Find critical points. $\frac{dA}{dx} = 2 -\frac{120}{x^2} = 0 ↭ \frac{120}{x^2} = 2 ↭ x^2 = 60 ↭ x = \sqrt{60} ≈ 7.746$

Determine whether critical points correspond to local maxima, local minima, or saddle points.

$\frac{d^2A}{dx^2} = \frac{240}{x^3}$ at x = $\sqrt{60},\frac{d^2A}{dx^2}=\frac{240}{x^3}\bigg|_{\sqrt{60}}$ > 0 ⇒ there exists a minimum.

Interpret the results. The dimensions of the garden that minimize the combined area of the garden and borders are x = $\sqrt{60}≈ 7.746$m and y = $\frac{30}{x} = \frac{30}{\sqrt{60}} ≈ 3.87m.$

• Find the area of the largest rectangle that can be inscribed in the ellipse, $\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1.$

Understand/Represent the problem.

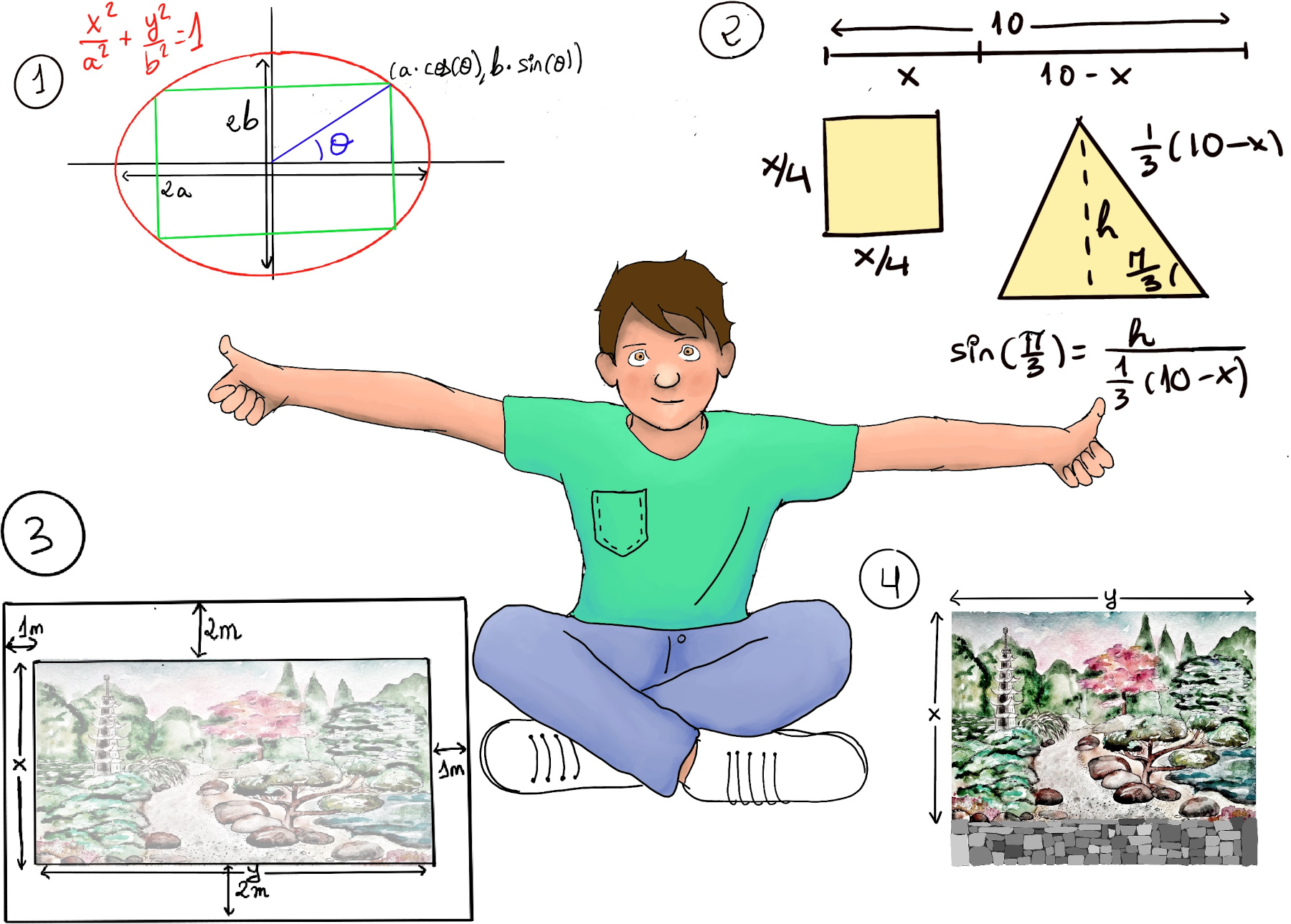
For a rectangle to be inscribed in the ellipse, the sides of the rectangle must be parallel to the axes, so its vertices are (±a·cos(θ), ±b·sin(θ)) (Figure 1). Recall that the parametric equations of an ellipse in standard form are: x(t) = a cos(t), y(t) = b sin(t) where: a is the length of the semi-major axis and b is the length of the semi-minor axis, and t is the parameter ranging from 0 to 2π.

Find the Objective Function. The rectangle area is A(θ) = l·w =[l = 2·a·cos(θ), w = 2·b·sin(θ)] 4·a·b·cos(θ)·sin(θ) = 2·a·b·sin(2θ).

Find critical points. $\frac{dA}{dθ} = 2·a·b·cos(2θ) = 0 ↭$[a ≠ 0, b ≠ 0] cos(2θ) = 0 ⇒ 2θ = $\frac{π}{2} ⇒ θ = \frac{π}{4}.$

Determine whether critical points correspond to local maxima, local minima, or saddle points. $\frac{d^2A}{dθ^2} = -4·a·b·sin(2θ), \frac{d^2A}{dθ^2}\bigg|_{\frac{π}{4}} = -4·a·b·sin(\frac{π}{2}) = -4·a·b < 0 ⇒ \frac{π}{4}$ is a maximum.

Interpret the results. The maximum area is A = 4·a·b·$cos(\frac{π}{4})sin(\frac{π}{4}) = \frac{4·a·b}{\sqrt{2}·\sqrt{2}} = 2ab.$

Example: Let the elipse be $\frac{x^2}{4}+y^2 = 1, a = 2, b = 1, Area = 2·2·1 = 4, θ = \frac{π}{4}$ and its vertices are (±a·cos(θ), ±b·sin(θ)) = $(±2·cos(\frac{π}{4}), ±1·sin(\frac{π}{4})) = (±2·\frac{1}{\sqrt{2}}, ±\frac{1}{\sqrt{2}}) = (±\sqrt{2}, ±\frac{1}{\sqrt{2}})$

• A piece of wire 10m long is cut into two pieces. One piece is bent into a square and the other is bent into an equilateral triangle. How should the wire be cut so that the total area enclosed is (a) a minimum and (b) a maximum?

Understand/Represent the problem (Figure 2).

The first piece will have length x which we’ll bend into a square. Each side of the square will have length $\frac{x}{4}$. Similarly, the second piece will have length 10 - x, and we will bend it into an equilateral triangle (a triangle that has three sides that are all the same length and three angles that are all the same size, namely 60° = $\frac{π}{3}$) ⇒ each side of the equilateral triangle will have length $\frac{1}{3}·(10-x)$.

$sin(\frac{π}{3})=\frac{\sqrt{3}}{2}=\frac{h}{\frac{1}{3}(10-x)}⇒ h = \frac{\sqrt{3}(10-x)}{6}$

Find the Objective Function. A =[A₁ = l², A₂ = $\frac{base*h}{2}$] A₁ + A₂ = $(\frac{x}{4})^2 + \frac{1}{3}(10-x)\frac{\sqrt{3}(10-x)}{6}·\frac{1}{2} = \frac{x^2}{16}+\frac{\sqrt{3}(10-x)^2}{36}$

Find critical points. $\frac{dA}{dx} = \frac{x}{8}-\frac{\sqrt{3}(10-x)}{18} = 0 ↭ (\frac{1}{8}+\frac{\sqrt{3}}{18})x = \frac{\sqrt{3}·10}{18} ↭ \frac{18x +\sqrt{3}·8·x}{8·18} = \frac{\sqrt{3}·10}{18} ↭ \frac{18 +\sqrt{3}·8}{8}x = \sqrt{3}·10 ↭ x = \frac{\sqrt{3}·80}{18 +\sqrt{3}·8}$ ≈ 4.35.

Determine whether critical points correspond to local maxima, local minima. $\frac{d^2A}{dx^2} =\frac{1}{8}+\frac{\sqrt{3}}{18} > 0 ⇒ x = \frac{\sqrt{3}·80}{18 +\sqrt{3}·8}$ ≈ 4.35 is a local minimum.

Interpret the results. The area is minimized when x = $\frac{\sqrt{3}·80}{18 +\sqrt{3}·8}$ ≈ 4.35 (that is used to make the square and so 5.65 is used to make a triangle) and A(4.35) ≈ 2.71. The area is maximized in the boundaries, more precisely when x = 10, that is, when all of the wire is used to make the square, A = $\frac{10^2}{16} ≈ 6.25$ (we have previously calculated A(x = 0) = $\frac{\sqrt{3}·10^2}{36}≈ 4.81 < 6.25$).

• A box with a square base and open top must have a fixed volume. Find the dimensions of the box that minimize the amount of material used.

Let x represent the base’s side, and y the height. V = x²y (fixed) ⇒ y = $\frac{V}{x^{2}}$

A = x²+4xy = x²+4^V⁄_x

$\frac{dA}{dt}$ = 2x -4^V⁄_x². $\frac{dA}{dt} = 0 ⇒ 0 = \frac{2x^{3}-4V}{x^{2}} ⇒ 0 = 2x^3-V $ ⇒ $x = \sqrt[3]{2V}$

1. (0, $\sqrt[3]{2V}$), $\frac{dA}{dt}$ < 0 ⇒ A is decreasing.
2. ($\sqrt[3]{2V}$, ∞), $\frac{dA}{dt}$ >0 ⇒ A is increasing. Therefore, x = $\sqrt[3]{2V}$ is a minimum, y = $\frac{V}{x^2}=\frac{V}{(2V)^{2/3}} = 2^{\frac{-2}{3}}V^{\frac{1}{3}}$

Futhermore, $\frac{x}{y}=\frac{2^{\frac{1}{3}}V^{\frac{1}{3}}}{2^{\frac{-2}{3}}V^{\frac{1}{3}}} = 2.$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.