Newton's Method

Face reality as it is, not as it was or as you wish it to be, Jack Welch.

Recall

The derivative of a function at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. It is the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable.

Definition. A function f(x) is differentiable at a point “a” of its domain, if its domain contains an open interval containing “a”, and the limit $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$ exists, f’(a) = L = $\lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$. More formally, for every positive real number ε, there exists a positive real number δ, such that for every h satisfying 0 < |h| < δ, then |L-$\frac {f(a+h)-f(a)}{h}$|< ε.

1. Power Rule: $\frac{d}{dx}(x^n) = nx^{n-1}$.
2. Sum Rule: $\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))$
3. Product Rule: $\frac{d}{dx}(f(x) \cdot g(x)) = f’(x)g(x) + f(x)g’(x)$.
4. Quotient Rule: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f’(x)g(x) - f(x)g’(x)}{(g(x))^2}$
5. Chain Rule: $\frac{d}{dx}(f(g(x))) = f’(g(x)) \cdot g’(x)$
6. $\frac{d}{dx}(e^x) = e^x, \frac{d}{dx}(\ln(x)) = \frac{1}{x}, \frac{d}{dx}(\sin(x)) = \cos(x), \frac{d}{dx}(\cos(x)) = -\sin(x), \frac{d}{dx}(\tan(x)) = \sec^2(x), \frac{d}{dx}(\arcsin(x)) = \frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arccos(x)) = -\frac{1}{\sqrt{1 - x^2}}, \frac{d}{dx}(\arctan(x)) = \frac{1}{1 + x^2}.$

The critical points of a function f are the x-values, within the domain (D) of f for which f’(x) = 0 or where f’ is undefined. Notice that the sign of f’ must stay constant between two consecutive critical points. If the derivative of a function changes sign around a critical point, the function is said to have a local or relative extremum (maximum or minimum) at that point. If f’ changes sign from positive (increasing function) to negative (decreasing function), the function has a local or relative maximum at that critical point. Similarly, if f’ changes sign from negative to positive, the function has a local or relative minimum.

Newton’s method

Newton’s method, also known as the Newton-Raphson method, is a root-finding algorithm, basically an iterative numerical technique, which produces successively better approximations to the root or zeroes of a real-valued function f(x).

It is widely used for solving nonlinear equations and finding roots of functions.

1. The idea is to start with an initial guess, hopefully a reasonable good guess, relatively close to the true root, e.g., x₀ = 2.

2. Then, we approximate the function by its tangent line, and calculate the x-intercept of this tangent line. This x-intercept is our new guess, say x₁, and it will typically be a better approximation to the original function's root than the first guess. This method is illustrated at the Figure 2.d. 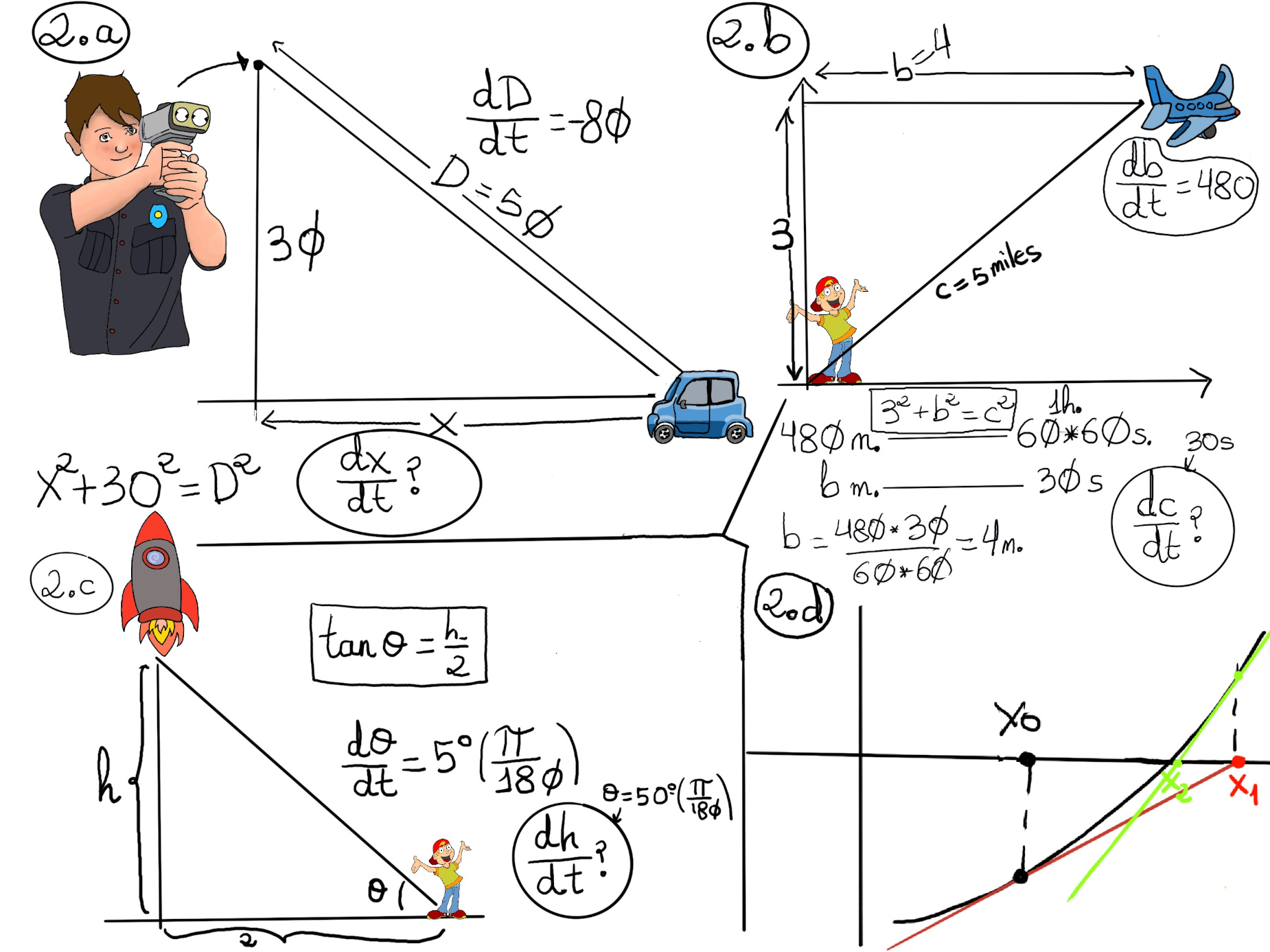  The tangent line’s formula is: $y-y_0=m(x-x_0)$

   x1 is the x-intercept, so $0-y_0=m(x_1-x_0) ⇒ x_1 = x_0 -\frac{y_0}{m} = x_0 -\frac{f(x_0)}{f’(x_0)}$

3. The process is repeated and refined $x_{n+1} = x_n - \frac{f(x_n)}{f’(x_n)}$ until it is close enough to the actual solution.

   Recall: The tangent line’s formula is: $y-y_n=m(x-x_n)$

   x_n+1 is the x-intercept, so $0-y_n=m(x_{n+1}-x_n) ⇒ x_{n+1} = x_n -\frac{y_n}{m} = x_n -\frac{f(x_n)}{f’(x_n)}$

Basic Principle

1. It starts with an initial guests x₀ for the root of the function, that is reasonable “good” or “close” to the true root.
2. Tangent Line Approximation. At each iteration, Newton’s method finds the tangent line to the graph of f(x) at the point (x_n, f(x_n)) and use the formula $x_{n+1} = x_n - \frac{f(x_n)}{f’(x_n)}$ to obtain a new, more accurate approximation, namely x_n+1, that is the root of this tangent line.
3. Iterative process. This process is repeated until an approximation to the root is close enough for the desired level of accuracy, meaning that is sufficiently close to zero or when the difference between successive approximations is below a specified level of tolerance.

This method is particularly efficient and quite effective for approximating solutions to equations, especially when the original guess is reasonably close to the actual solution and the function is well-behaved. However, it may not converge or may converge to a local minimum or maximum if the initial guess is far from the actual root.

Additionally, Newton’s method requires the derivative of the function, which may not always be readily available or computationally expensive to compute.

Solved examples

• Find an approximation of $\sqrt{2}$, x₀ = 1.

We need to find the root of f(x) = x²-2, f’(x) = 2x.

$x_1 = x_0 -\frac{f(x_0)}{f’(x_0)} =1 -\frac{-1}{2}=\frac{3}{2} = 1.5.$

$x_2 = x_1 -\frac{f(x_1)}{f’(x_1)} =1.5 -\frac{\frac{9}{4}-2}{3} ≈ 1.416.$

$x_2 = x_1 -\frac{f(x_1)}{f’(x_1)} =1.416 -\frac{1.416^2-2}{2·1.416} ≈ 1.41421,$ that is a pretty good approximation.

• Find an approximation of the root for x³ +x -1 = 0 near x = 1.

Let f(x) = x³ +x -1, f’(x) = 3x² +1, and we are told x₀ = 1.

$x_1 = x_0 -\frac{f(x_0)}{f’(x_0)} =1 -\frac{1+1-1}{3·1+1}=1 - \frac{1}{4} = \frac{3}{4} = 0.75.$

$x_2 = x_1 -\frac{f(x_1)}{f’(x_1)} =0.75 -\frac{0.75^3+0.75-1}{3·0.75^2+1} ≈ 0.697.$

$x_3 = x_2 -\frac{f(x_2)}{f’(x_2)} = 0.697 -\frac{0.697^3+0.697-1}{3·0.697^2+1} ≈ 0.6854.$

Notice that $0.6854^3 +0.6854 -1 = 0.007382523864$, so it is a really good approximation.

• Calculate a root for x⁵-5x + 3 = 0. Let f(x) = x⁵-5x + 3. Notice that f is continuos, f(1) = 1⁵-5·1 + 3 = -1 < 0, f(2) = 2⁵ -5·3 + 3 = 25 > 0 ⇒ By the Intermediate Value Theorem, ∃a ∈ (1, 2), a solution of f.

A reasonably good guess is x₀ = 2. f’(x) = 5x⁴ -5. $x_1 = x_0 -\frac{f(x_0)}{f’(x_0)} = 2 - \frac{2^5-5·2+3}{5·2^4-5} = \frac{5}{3} ≈ 1.66667$

$x_2 = x_1 -\frac{f(x_1)}{f’(x_1)} = 1.66667 - \frac{1.66667^5-5·1.66667+3}{5·1.66667^4-5} ≈ 1.4425.$

$x_3 = x_2 -\frac{f(x_2)}{f’(x_2)} = 1.4425 - \frac{1.4425^5-5·1.4425+3}{5·1.4425^4-5} ≈ 1.3204.$

$x_4 = x_3 -\frac{f(x_3)}{f’(x_3)} = 1.3204 - \frac{1.3204^5-5·1.3204+3}{5·1.3204^4-5} ≈ 1.2800.$

Notice that 1.2800⁵-5·1.2800+3 = 0.0359738368, that is not the solution, but close enough for most purposes. Another iteration is x₅ ≈ 1.2757, 1.2757⁵-5·1.2757+3 ≈ 0.00015.

• Apply two iterations of Newton’s method to approximate the x-value of a point of intersection of x²-4 and 2x-3 using as a initial guess x₀ = 0.

f(x) = x²-4 -2x +3 = x² -2x -1, f’(x) = 2x -2.

$x_1 = x_0 -\frac{f(x_0)}{f’(x_0)} = 0 - \frac{-1}{-2} = -\frac{1}{2}$.

$x_2 = x_1 -\frac{f(x_1)}{f’(x_1)} = -\frac{1}{2} - \frac{(-\frac{1}{2})^2-2·(-\frac{1}{2})-1}{2·-\frac{1}{2}-2} = -\frac{1}{2} - \frac{\frac{-1}{4}+1-1}{-1-2} = -\frac{1}{2}+\frac{1}{12} = \frac{-5}{12}$.

Notice that $(\frac{-5}{12})^2-4≈-3.826389$ and also $2·\frac{-5}{12}-3 ≈ -3.833333$ that shows that is really a good approximation after only two iterations.

• Let’s approximate $\sqrt[7]{1000}$. It is the same as trying to find the root of f(x)=x⁷ - 1000.

A reasonably good guess is x₀=3. f’(x)=7x⁶, $x_1 = x_0 -\frac{f(x_0)}{f’(x_0)} = 3 - \frac{3^{7}-1000}{7·3^{6}}≈2.76739173$

$x_2 = x_1 -\frac{f(x_1)}{f’(x_1)} = 2.76739173 - \frac{2.76739173^{7}-1000}{7·2.76739173^{6}}≈2.69008741$

$x_3 = x_2 -\frac{f(x_2)}{f’(x_2)} = 2.69008741 - \frac{2.69008741^{7}-1000}{7·2.69008741^{6}}≈2.68275645$. Google’s search engine returns 2.68269579528 ($\sqrt[7]{1000}$), so it is quite a good approximation.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.