The Natural Numbers. The Binomial Theorem.

There is nothing more practical than a good theory, Leonid Brezhnev.

The natural numbers

A natural number is a mathematical object. It is a number that occurs commonly in nature. As such, it is a whole, non-negative number, that is, a member of the sequence 0, 1, 2, 3, …, obtaining by starting from zero and adding 1 successively. The set of natural number is denoted by ℕ. Hence, ℕ = {0, 1, 2, 3, …}.

Natural numbers can be added and multiplied, i.e., if m and n are natural numbers, then m + n and m x n (aka m·n or mn) are also natural numbers.

Zero is the additive identity for whole numbers, i.e., when Zero is added to any whole number, the resultant number is the given whole number itself: n + 0 = n, ∀n ∈ ℕ (meaning for all n numbers in the natural numbers).

One is the multiplicative identity of whole numbers. If we multiply one to any whole number, the result will be the same whole number: n x 1 = n, ∀ n ∈ ℕ

Natural numbers have order, addition, and multiplication.

Definition. Let m and n be two arbitrary natural numbers. We write m ≤ n to mean or express that there exists another natural number k such that m + k = n. Sometimes, this is written more concisely as ∀m, n ∈ ℕ, m ≤ n ⇒ ∃k ∈ ℕ: m + k = n.

It satisfies three properties: reflexive (n ≤ n), antisymmetric (if n ≤ m and m ≤ n, then n = m), and transitive (if n ≤ l, l ≤ m, then n ≤ m).

Proof (transitive)

Let’s assume that n ≤ l, l ≤ m ⇒ ∃k, k’∈ ℕ such that l = n + k, m = l + k’ ⇒ m = (n + k) + k’ = [By Associativity] n + (k + k’) ⇒ ∃ (k + k’) = k’’∈ ℕ: m = n + k’’ ⇒ n ≤ m∎

Given the set ℕ of natural number and the successor map or function s: ℕ → ℕ, sending each natural number to the next one, the natural numbers could be defined recursively as follows, 0 = {} = ∅, 1 = {1}, 2 = {0, 1},... where the successor function is s(n) = n ∪ {n} and satisfies,

1. s is injective, that is, for all natural numbers, say n, m ∈ ℕ, if s(x) = s(y), then x = y.
2. 0 ∉ Range(s), that is, for every natural number n ∈ ℕ, s(n) = 0 is false.
3. Mathematical induction: if M ⊆ ℕ with 0 ∈ M and s[M] ⊆ M, then M = ℕ.

Definition. Let’s define addition on ℕ using the following axioms or rules, (recursive definition, rd for short)
(i) m + 0 = m, ∀ m ∈ ℕ
(ii) m + s(n) = s(m + n), ∀ n, m ∈ ℕ

Let’s denote s(n) = n + 1, the axioms above can be rewritten more concisely as:
(i) m + 0 = m, ∀ m ∈ ℕ
(ii) m + (n + 1) = (m + n) + 1, ∀ n, m ∈ ℕ

Mathematical induction can be also expressed in a more conventional fashion. Let P(n) be a property for natural numbers.
(i) Base case: If P(0) is true.
(ii) Induction step: ∀n ∈ ℕ: P(n) is true ⇒ P(n + 1) is also true.
Then, P(n) is true ∀n ∈ ℕ.

Associativity. The operation of addition on the set of natural numbers ℕ is associative, that is, x + (y + z) = (x + y) + z, ∀ x, y, z ∈ ℕ

Proof.

P(n): ∀x, y ∈ ℕ: x + (y + n) = (x + y) + n

• Case base. n = 0. Then, LHS = x + (y + 0) = x + y = (x + y) + 0 = RHS, ∀ x, y ∈ ℕ
• Induction step. Let’s suppose the proposition is true for n, and consider the case n + 1. Then, ∀ x, y ∈ ℕ,

LHS = x + (y + (n + 1)) = [rule (ii) addition’s definition] x + ( (y + n) + 1) = [rule (ii) addition’s definition] ( x + (y + n) ) + 1 = [inductive hypothesis] ( (x + y) + n ) + 1 = [rule (ii) addition’s definition] (x + y) + (n + 1) = RHS. And therefore, by the induction principle, the expression is true ∀ x, y, and n ∈ ℕ.

Definition. Multiplication is a map or function, · (or “x”): ℕ → ℕ. It can be defined recursively on ℕ by the following rules,
(i) 0 · m = 0, ∀ m ∈ ℕ
(ii) (n + 1) · m = (n · m) + m, ∀ n, m ∈ ℕ.

The multiplication has the following properties: (∀ n, m ∈ ℕ)

1. Associative: n · (m · k) = (n · m) · k
2. Commutative: n · m = m · n
3. Neutral element: ∃1 ∈ ℕ: 1 · n = n
4. Distributive: n · (m + k) = n · m + n · k

Proof by induction (Distributive law)

• Case base: 0 · (m + k) = 0 = 0 · m + 0 · k
• Induction step: (n + 1) · (m + k) = [Recursive definition of multiplication] n · (m + k) + (m + k) = [Induction hypothesis] n · m + n · k + (m + k) = [Recursive definition of multiplication] = [Associativity] n · m + (n · k + m) + k = [Commutative] n · m + (m + n · k) + k = [Associativity] (n · m + m) + (n · k + k) = [Recursive definition of multiplication] (n + 1)·m + (n + 1) · k∎

Definition. Let’s define factorial n! on ℕ by the following rules,
(i) 0! = 1
(ii) (n + 1)! = n! × (n + 1), ∀ n ∈ ℕ

Theorem. Well-ordering property of the natural numbers. Every non-empty subset of the natural numbers has a least or minimal element.

The set of natural number ℕ is well-ordered. On the contrary, ℤ, ℚ, and ℝ are ordered set, but are not well-ordered since minimal elements need not exist in their subsets.

Proof. Suppose that there is a non-empty subset S that does not have a least element. Let’s define S* to be the complement of S, that is, the set of natural numbers that are not in S.

Let P(n) be the statement that S* contains n.

• Case base. 0 ∉ S, since if zero were in S, then S would obviously have a minimal element, namely zero, and therefore P(0) is true.
• Induction step. Let’s suppose P(0),…,P(n) hold (Strong induction). Then, n + 1 ∉ S, because if n + 1 were in S, then it would necessary be the minimum element of S since by the inductive hypothesis all the smaller elements of ℕ are not in S. Therefore, n + 1 ∈ S*, P(n+1) holds.

By the strong induction property, n ∈ S* ∀ n ∈ ℕ, and as consequence S = ∅ (empty)⊥, i.e., a contradiction with our initial assumption that S is a non-empty subset.

• Prove that the sum of the first odd natural numbers is n², 1 + 3 + 5 + … + (2n -1) = n².

For the sake of contradiction, let’s suppose the equation is false. Let S be the set of all counterexamples to this equation ⇒ [Well-Ordering Principle] there is a minimal element k in S: 1 + 3 + 5 + … + (2k -1) ≠ k², and k ≠ 1 (we know that the equation holds for k = 1, 1² = 1)) ⇒ [k is a minimal element in S] the equation holds for k-1: 1 + 3 + 5 + … + (2(k-1) -1) = (k-1)² ⇒ [Let’s add (2k -1) to both sides of the equation] 1 + 3 + 5 + … + (2k -3) + (2k -1) = (2k -1) + (k-1)² = 2k -1 + k²+1 -2k = k² ⊥ (k ∈ S^*)

• Commutative. The operation of addition on the set of natural numbers ℕ is commutative, that is, x + y = y + x, ∀ x, y ∈ ℕ

First, we prove the base cases y = 0, y = 1, i.e., we prove that 0 and 1 commute with everything.

• y = 0, x + 0 = x = 0 + x, ∀ x ∈ ℕ
• y = 1. Let P(n) be the statement that n + 1 = 1 + n

(i) n = 0, 0 + 1 = 1 = 1 + 0, and therefore P(0) holds.
(ii) Let’s suppose P(n) is true, that is, n + 1 = 1 + n.

(n + 1) + 1 = [inductive hypothesis] (1 + n) + 1 = [Associative property] 1 + (n + 1), P(n + 1) holds.

• Next, let’s suppose that x + y = y + x.

x + (y + 1) = [Associative property] (x + y) + 1 = [By the induction hypothesis] (y + x) + 1 = [Associative property] y + (x + 1) = [As it has been shown above, the natural numbers zero and one commute with everything] y + (1 + x) = [Associative property] (y + 1) + x ∎

To sum up, the addition of natural numbers + is a map or function, +: ℕ x ℕ → ℕ with the following properties: ∀m, n, k ∈ ℕ,

• Neutral element. ∃0 ∈ ℕ: m + 0 = m
• Associative law: (k + m) + n = k + (m + n)
• Commutative law: m + n = n + m.

The Binomial Theorem

In combinatorics, the binomial coefficient is used to denote the number of possible ways to choose or pick k elements from a larger set of size n. In other words, it is the number of ways of picking k outcomes from n possibilities.

1. Permutation with Repetition. A permutation is an arrangement of objects in a particular way or order. Example: Permutations to a three-digit lock is n^k = 10³ where n is the number of things to choose from, and we pick or select k of them, repetition is allowed and order matters.

2. Permutation without Repetition. Example: We have 8 people (say Alice, Bob, Charles, ···, H). How many ways can we award a 1st, 2nd, and 3rd place prize among eight contestant? Sol: 8 (8 choices for gold metal) x 7 (7 choices for silver medal) x 6 (bronze). Another way of thinking about it is this: G (gold) S (Silver) B (bronze) NS ··· NS (There are 5 Non selected). If we have n items or elements and want to select k in a certain order, the solution is P(n, k) = $\frac{n!}{(n-k!)} = \frac{8!}{(8-3)!}$ No repetitions, order matters. We remove (8-3)! because we are only interested in the first three selections (G, S, B) and get rid of everyone else (NS ···₅ NS). The order of losers is completely irrelevant, that is, Alice Bob Charlie NS₁ NS₂ ··· NS₅ = Alice Bob Charlie NS₂ NS₁ ··· NS₅ = ···

3. A combination is a selection of k items from a set of n items such that we don't care about the order of selection. Repetition is not allowed. How can I give three diplomas to 8 people? Well, in this case, the order we pick people does not matter, so Diploma→Alice, Diploma→Bob, Diploma→Charlie is the same as giving to Diploma→Bob, Diploma→Alice, Diploma→Charlie, and so on. The general formula is ⁿC_k, C(n, k) = $\frac{n!}{(n-k)!k!} = \frac{8!}{(8-5)!3!} = 56$ where we just create all the permutations and divide by all the redundancies, that is, 3! ways to rearrange the three winners (those who receive the diplomas) and 5! ways to rearrange the losers.

Example. You are a disc jockey at a wild party, select three love songs from a list of 10 romantic ballads. C(10, 3) = $\frac{n!}{(n-k)!k!} = \frac{10!}{(10-3)!3!} = 120$.

Definition. The value of the binomial coefficient for natural numbers n and k is read as “n choose k”, denoted as ⁿC_k, C(n, k) or $\binom{n}{k}$, and given by,
$\binom{n}{k} = $ ^n!⁄_k!(n-k)! for 0 ≤ k ≤ n.
$\binom{n}{k} = $ 0 if k > n.

Pascal’s triangle is an arrangement of binomial coefficient in triangular form, in which the nth row contains the n + 1 possible values of k, that is, $\binom{n}{k}$. The numbers are placed in such a way that each number is the sum of the two entries or numbers just above it. It is used widely in probability theory, combinatorics, and algebra. 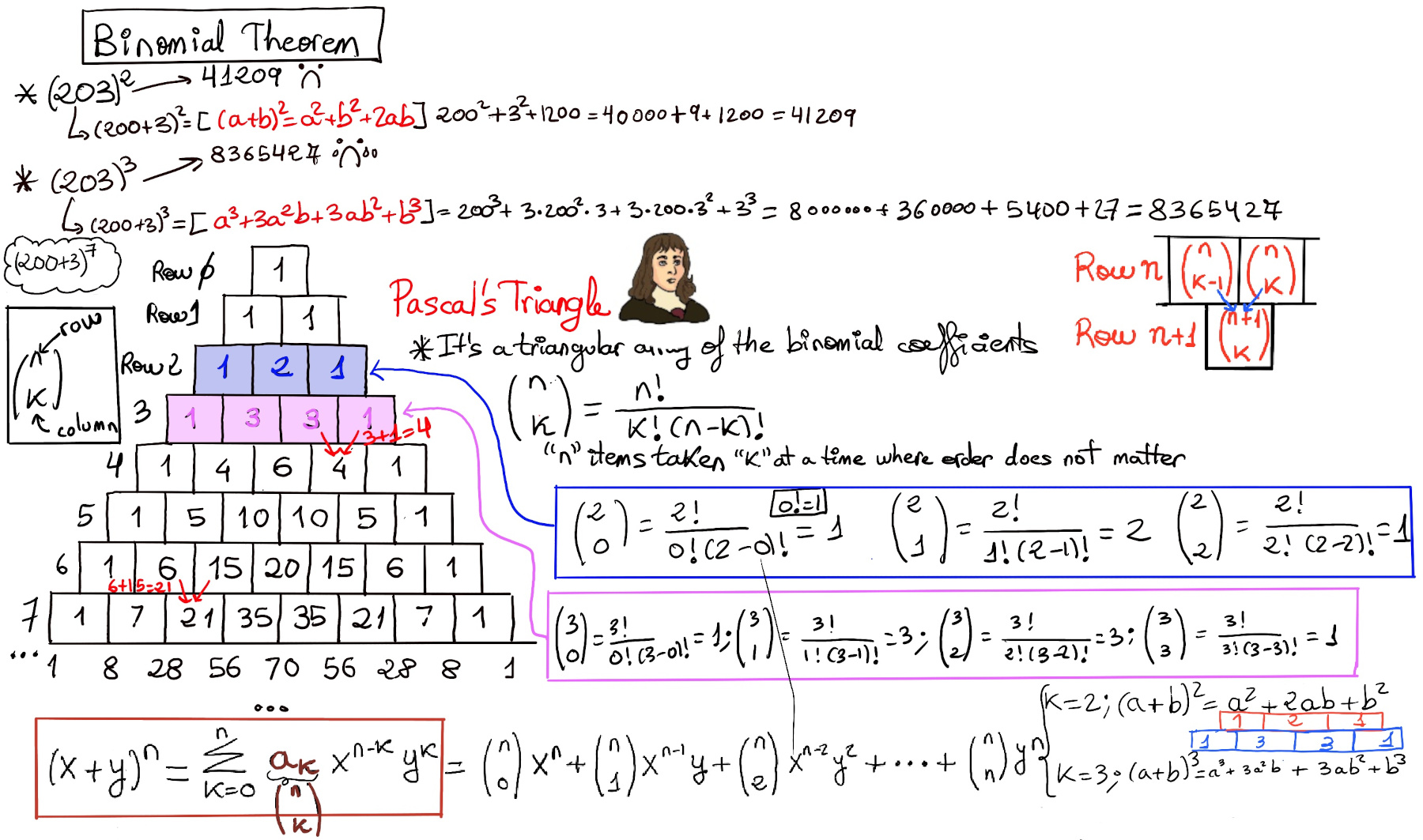  Pascal’s Triangle. Let n and k be natural numbers with 1 ≤ k ≤ n. Then, the following formula applies, $\binom{n}{k-1}$ + $\binom{n}{k}$ = $\binom{n+1}{k}$

Proof: $\binom{n}{k-1}$ + $\binom{n}{k}$ = ^n!⁄_{(k-1)!(n-k+1)!} + ^n!⁄_k!(n-k)! = ^{n!k + n!(n-k+1)}⁄_k!(n-k+1)! = ^{n!(k + n -k +1)}⁄_k!(n-k+1)! = ^{(n + 1)!}⁄_k!(n+1-k)! = $\binom{n+1}{k}$

Binomial Theorem. It describes the algebraic expansion of powers of a binomial. Let x and y be real numbers, and n be any natural number, it states that the nth power of the sum of both numbers x and y may be expressed as the sum of n+1 terms of the form, (x+y)ⁿ = $\sum_{k=0}^{n}\binom{n}{k}x^ky^{n-k}$

Proof. (i) n = 0, (x+y)⁰ = 1, $\sum_{k=0}^{0}\binom{0}{k}x^ky^{-k}$ = 1

(ii) Let’s suppose the expression holds for n.

(x+y)⁽ⁿ⁺¹⁾=(x+y)(x+y)ⁿ = [by the inductive hypothesis] (x+y)($\sum_{k=0}^{n}\binom{n}{k}x^ky^{n-k}$) = $\sum_{k=0}^{n}\binom{n}{k}x^{k+1}y^{n-k}$ + $\sum_{k=0}^{n}\binom{n}{k}x^ky^{n+1-k}$ = xⁿ⁺¹ + $\sum_{k=0}^{n-1}\binom{n}{k}x^{k+1}y^{n-k}$ + $\sum_{k=1}^{n}\binom{n}{k}x^ky^{n+1-k}$ + yⁿ⁺¹

We set k as l - 1,

= xⁿ⁺¹ + $\sum_{l=1}^{n}\binom{n}{l-1}x^{l}y^{n+1-l}$ + $\sum_{k=1}^{n}\binom{n}{k}x^ky^{n+1-k}$ + yⁿ⁺¹ = [relabelling k as l] xⁿ⁺¹ + $\sum_{k=1}^{n}${$\binom{n}{k-1}+\binom{n}{k}$}$x^{k}y^{n+1-k}$ + yⁿ⁺¹ = [Pascal’s Triangle] xⁿ⁺¹ + $\sum_{k=1}^{n}\binom{n+1}{k}x^{k}y^{n+1-k}$ + yⁿ⁺¹ = $\sum_{k=0}^{n+1}\binom{n+1}{k}x^{k}y^{n+1-k}$ ∎

Bibliography:

1. Math Typesettings in Hugo, mertbakirc
2. Oxford Mathematics