Logarithm functions

Recall

You have to be Odd, to be number one. Copy from one, it’s plagiarism; copy from three or more, it’s research.

American actress Ilka Chase enjoyed success as a novelist. In one encounter, an anonymous actress said to her: “I enjoyed reading your book. Who wrote it for you?” …to which Chase replied: “Darling, I’m so glad that you liked it. Who read it to you?”

Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).

The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ.

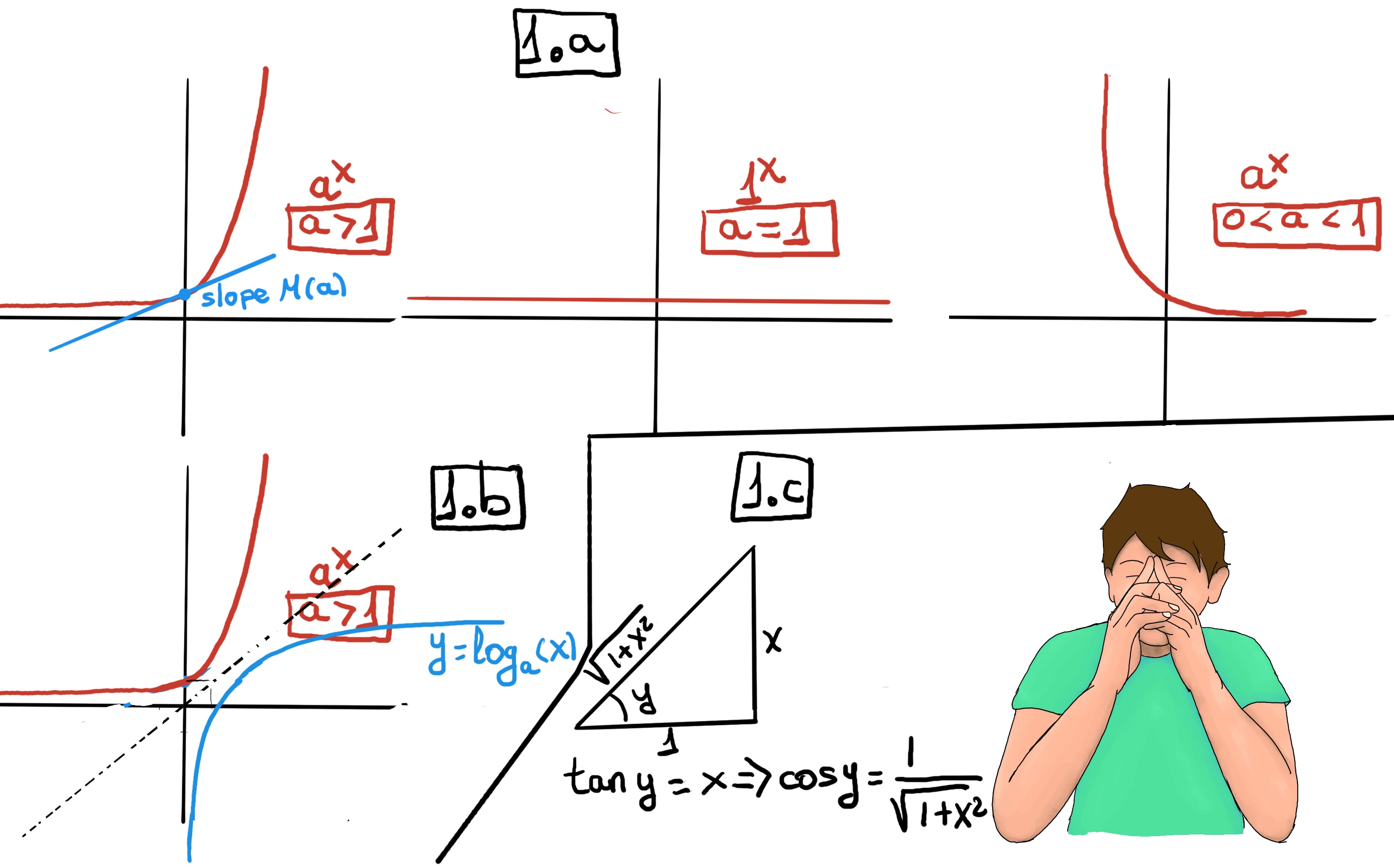
An exponential function is a mathematical function of the form f(x) = b·a^x, where the independent variable is the exponent, and a and b are constants. a is called the base of the function and it should be a positive real number (a>0).

Examples are 2^x, 7^x, and (¹⁄₄)^x. There are three kinds of exponential functions depending on whether a > 1, a = 1, 0 < a < 1 -1.a.-

1. If a > 1, it can be observed that as the exponent increases, the curve get steeper. As x increases, f(x) heads to infinity, $\lim_{x \to ∞} a^x = ∞$. As x decreases, f(x) heads to zero, $\lim_{x \to -∞} a^x = 0$. It is strictly increasing and has a horizontal asymptote along the x-axis.

   It is important to realize that as x approaches negative infinity, the results become very small but never actually attain zero, e.g., 2^-5 ≈ 0.03125, 2^-15 ≈ 0.00003052. Besides, the base of an exponential function determines the rate of growth or decay. For a > 1, the larger the base, the faster the function grows.

2. 0 < a < 1. As x increases, f(x) heads to zero, $\lim_{x \to ∞} a^x = 0$. As x decreases, f(x) heads to ∞, $\lim_{x \to -∞} a^x = ∞$. It is strictly decreasing and has a horizontal asymptote along the x-axis.
3. When a = 1, the graph is a horizontal line, y = 1.  

Loosely speaking, the inverse function of a function f is a function that undoes the operation of the original function. If f is a function that maps each element x in its domain to a unique element y in its codomain, then the inverse function, denoted as $f^{-1}$, maps each y back to its corresponding x.

For a given function f, its inverse g(=f^-1) is a function that reverses its result (g reverses the input and output of the original function), g(f(x))=x. An example is f(x)=$\sqrt{x},$ (x ≥ 0) g(f(x))=x ↭ g(x)= x², the square function (x²) is the inverse of the square root function ($\sqrt{x}$).

Logarithm function

In mathematics, the logarithm is the inverse function to exponentiation. We call the inverse of a^x the logarithmic function with base a, that is, log_ax=y ↔ a^y=x, that means that the logarithm of a number x to the base a is the exponent to which a must be raised to produce x, e.g., log₄(64) = 3 ↭ 4³ = 64, log₂(16) = 4 ↭ 2⁴ = 16, log₈(512) = 3 ↭ 8³ = 512, but log₂(-3) is undefined.

The logarithm function is a type of mathematical function which is helpful in many areas of science, such as finance, biology, and physics. For example, investors use logarithms to calculate compound interest. Various solutions to applied mathematical issues can be done by using logarithms, such as radioactive decay and nuclear waste, the elimination of medicines from the body, etc.

Although the base of a logarithm can be any number, the most common bases used are 10 and e. The logarithm with base e is the natural logarithm. The natural logarithm is the inverse of e^x, that is, lnx=y ↔ e^y=x where e is the Eulers Number, a mathematical constant approximately equal to 2.71828.

The logarithm’s domain consists of real positive numbers. Its range is ℝ (figure i and ii). x-intercept: (1, 0), y-intercept: none. It is one-to-one and has a vertical asymptote along the y-axis at x = 0.

1. If a > 1, it can be observed that as the value of the argument increases, the logarithm’s value increases as well. As x increases, f(x) heads to infinity, $\lim_{x \to ∞} log_a(x) = ∞$. As x decreases, f(x) heads to zero, $\lim_{x \to 0+} log_a(x) = 0$. It is strictly increasing and has a vertical asymptote along the y-axis at x = 0.

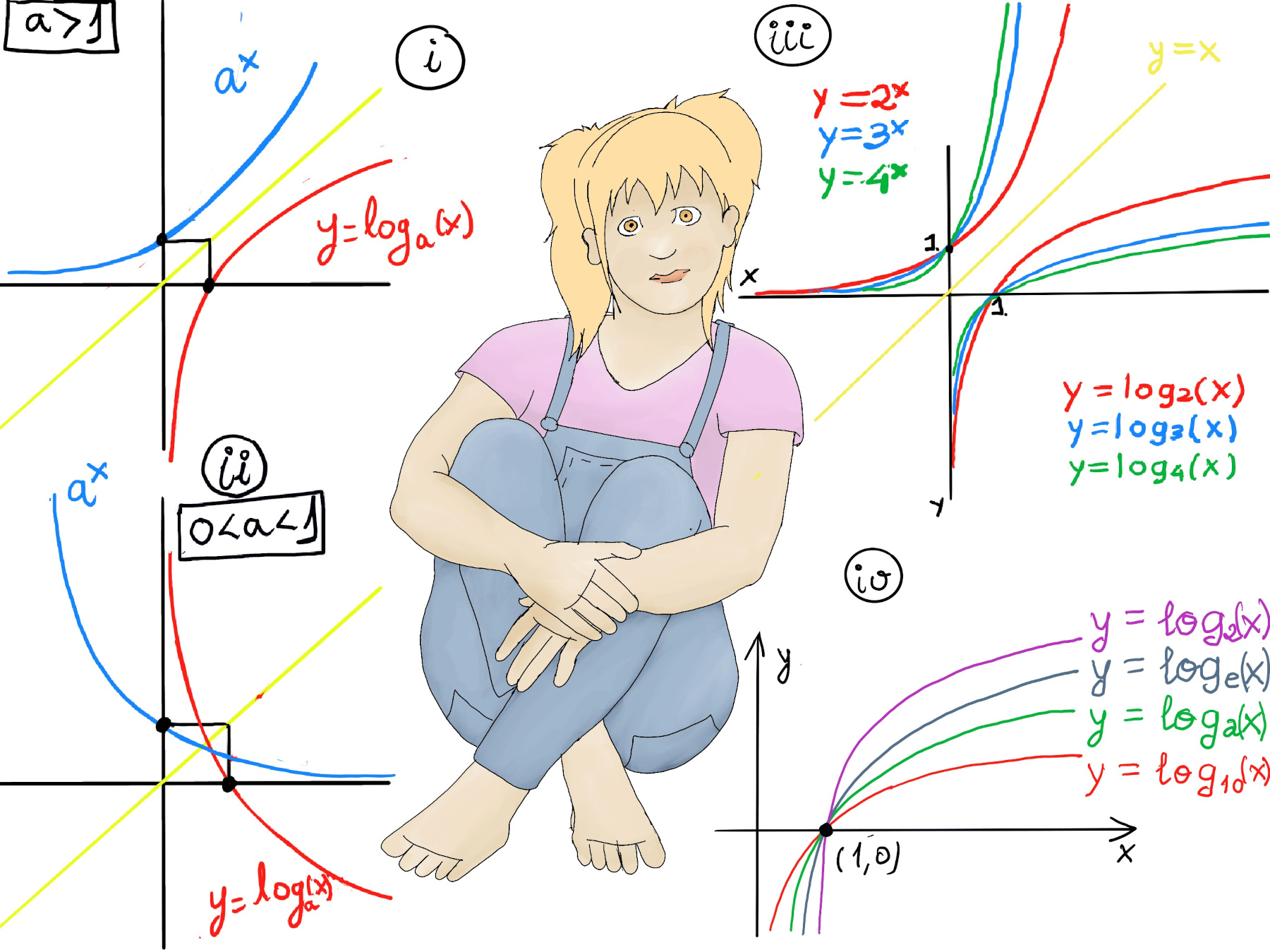
   The bigger the logarithm base, the graph approaches the asymptote of x = 0 quicker (Figure iii and iv).

2. If 0 < a < 1, it can be observed that as the value of the argument increases, the logarithm’s value decreases. As x increases, f(x) heads to minus infinity, $\lim_{x \to ∞} log_a(x) = -∞$. As x decreases, f(x) heads to zero, $\lim_{x \to 0+} log_a(x) = 0$. It is strictly decreasing and has a vertical asymptote along the y-axis at x = 0.

Logarithmic Properties

1. Product Rule. log_a(xy)=log_a(x) + log_a(y).
2. Quotient Rule. log_a(^x⁄_y) = log_a(x) - log_a(y).
3. Power Rule. log_a(xⁿ) = n·log_a(x).
4. log_a(1) = 0 ↭ a⁰ = 1.
5. log_a(a) = 1 ↭ a¹ = a.

Derivate of the Logarithmic Function

If x > 0, y = ln(x) ⇒ e^y = x ⇒[Differentiating both sides of this equation. Recall exponential function (e^x)’=e^x] $e^y\frac{dy}{dx} = 1 ⇒ \frac{dy}{dx} = \frac{1}{e^y} = \frac{1}{x}.$

If x > 0, a ≠ 1, y = log_a(x) ⇒ a^y = x ⇒ ln(a^y) = ln(x) ⇒[Power Rule. log_a(xⁿ) = n·log_a(x).] y·ln(a) = ln(x) ⇒ y = $\frac{ln(x)}{ln(a)}⇒$[¹⁄_ln(a) is a constant] $\frac{dy}{dy} = \frac{1}{xln(a)}$.

Examples:

• f(x) = $ln(\frac{x}{x+1})$

f(x) = $ln(\frac{x}{x+1}) = ln(x)-ln(x+1)$

f’(x) = $\frac{1}{x}-\frac{1}{x+1} = \frac{x+1}{x(x+1)} -\frac{x}{x(x+1)} = \frac{1}{x(x+1)}$

• f(x) = $ln(\frac{x^2·sin(x)}{2x+1})$

f(x) = $ln(\frac{x^2·sin(x)}{2x+1}) = ln(x^2·sin(x))-ln(2x+1) = ln(x^2)+ln(sin(x))-ln(2x+1)= 2ln(x) +ln(sin(x))-ln(2x+1)$

f’(x) = $\frac{2}{x} + \frac{cos(x)}{sin(x)} -\frac{2}{2x+1} = \frac{2}{x} + cot(x) -\frac{2}{2x+1}$

• f(x) = x^x.

y = x^x ⇒ ln(y) = ln(x^x) ⇒ ln(y) = xln(x) ⇒ $\frac{d}{dx} ln(y) = \frac{d}{dx} xln(x) ⇒ \frac{y’}{y} = ln(x)+1 ⇒ y’ = y(ln(x)+1) = x^x(ln(x)+1).$

Change of Base of Logarithm

Let log_a(x) be the logarithm to base a of x. Then, $log_b(x)=\frac{log_a(x)}{log_a(b)}$.

Proof.

Let y = log_b(x) ↭ b^y = x and z = log_a(x) ↭ a^z = x.

Then, z = log_a(x) = $log_a(b^y) = y·log_a(b) ⇒ log_b(x) = y = \frac{z}{log_a(b)} = \frac{log_a(x)}{log_a(b)}∎$

Examples:

• Let’s convert $\log_2(9)$ to base e (natural logarithm), $log_2(9)=\frac{ln(9)}{ln(2)}$= [$ln(9) \approx 2.1972, ln(2) \approx 0.6931$] ≈ 3.1699 ≈ 3.17.

• $log_3(81)=\frac{log_{10}(81)}{log_{10}(3)}$= [$log_{10}(81) \approx 1.9082, log_{10}(3) \approx 0.4771$] ≈ 4.

Solved examples

• Simplify $log_8(\frac{1}{12})+log_8(\frac{12}{5})$

$log_8(\frac{1}{12})+log_8(\frac{12}{5})$ =[Product Rule. log_a(xy)=log_a(x) + log_a(y)] $log_8(\frac{1}{12}·\frac{12}{5}) = log_8(\frac{1}{5}).$

• Solve ln(4x-3) = 7.

ln(4x -3) = 7 ⇒[Apply e^x to both sides] $e^{ln(4x-3)} = e^7 ⇒ 4x -3 = e^7 ⇒ x = \frac{e^7+3}{4}.$

• Solve log₄(x²-2x) = log₄(5x-12).

log₄(x²-2x) = log₄(5x-12) ⇒[a = 4 > 1, logarithm is strictly increasing⇒ one-to-one] x²-2x = 5x-12 ⇒ x² -7x + 12 = 0 ⇒ (x-3)(x-4) = 0 ⇒ x = 3 or 4.

It is essential to make sure to plug these numbers into the original equation so we don’t end up taking logarithms of zero or negative numbers.

log₄(3²-2·3) = log₄(3) = log₄(5·3-12) and log₄(4²-2·4) = log₄(8) = log₄(5·4-12).

• Solve the logarithmic equation $log_3(\sqrt{-7x+1})-7 = -4$

$log_3(\sqrt{-7x+1})-7 = -4$⇒[Isolate the Logarithmic Term] $log_3(\sqrt{-7x+1}) = 3$⇒[Convert to Exponential Form] $3^{log_3(\sqrt{-7x+1})}=3^3 = 27 ⇒ \sqrt{-7x+1} = 27$ ⇒[Square both sides of the equation to solve for x] -7x+1 = 27² = 729 ⇒ -7x = 728 ⇒ $x = \frac{-728}{7}$ = -104.

Besides, $log_3(\sqrt{-7·-104+1})-7 = -4↭log_3(\sqrt{729})-7 = -4 ↭ log_3(27)-7 = -4 ↭ 3-7 = -4$ and obviously $log_3(\sqrt{729})$ is a valid number.

• Solve the logarithmic equation $log_3(2x+1)+log_3(x+8)=3$

$log_3(2x+1)+log_3(x+8)=3$⇒[Product Rule. log_a(xy)=log_a(x) + log_a(y)] $log_3((2x+1)(x+8)) = 3 ⇒$[By definition of logarithms] (2x+1)(x+8) = 3³ = 27.

Expand and rearrange the equation, 2x² +17x +8 = 27. It has two solutions x = -¹⁹⁄₂, x = 1.

It is essential to make sure to plug these numbers into the original equation so we don’t end up taking logarithms of zero or negative numbers.

1. $log_3(2\frac{-19}{2}+1)= log_3(-18)$ ⊥ Since logarithms of negative numbers are undefined, this is not a valid solution.
2. $log_3(2·1+1)+log_3(1+8)=3↭log_3(3)+log_3(9)=3↭1+2=3$, so 1 is a valid solution.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.